自由落体式绝对重力仪中重力加速度精度的优化

胡　明　张为民　田　蔚　钟　敏

1　中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉市徐东大街340号，430077



自由落体式绝对重力仪中重力加速度精度的优化

胡明1张为民1田蔚1钟敏1

1中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉市徐东大街340号，430077

摘要：针对等时间间隔与等距离间隔两种工作模式，给出绝对重力仪中初始位移、初始速度、重力加速度等参数精度的极限表达式。详细讨论了重力加速度拟合精度随分频数、初始速度及数据段选取的变化，结果表明，通过增加分频数、降低初始速度、选择合适数据段等方法能提高重力值的精度。

关键词：绝对重力仪；自由落体；数据段；等时间间隔；等距离间隔

FG5绝对重力仪的测量精度为μGal级。文献[1]利用单次自由落体产生的200个数据点中的45个即可满足精度需求，但未讨论自由落体数据点数的选取；文献[2]从频域上对重力仪的传递函数进行分析，并对比分析等时间间隔与等距离间隔两种数据处理模式；文献[3]从时域上对自由落体各数据权重进行讨论，但如何进一步设置干涉条纹分频数和选取合适的自由落体数据段，对重力值拟合精度进行优化，仍是一个值得深入研究的问题。本文针对自由落体式绝对重力仪，结合等时间间隔与等距离间隔两种模式，对比分析了自由落体中干涉条纹分频数、自由落体数据段选取等因素对重力值g拟合精度的影响。

1　自由落体重力加速度拟合精度

对于自由落体式高精度绝对重力仪，若忽略重力梯度效应，则位移xi1与时间ti的关系为:

(1)

式中x0、v0、g分别表示初始位移、初始速度与当地重力加速度，M表示干涉条纹分频数，λ为激光波长。通过等效高度计算可将重力值归算到自由落体的起始点，而高程改正能够将重力值改正到观测点。若地表重力梯度为γ，则自由落体方式中位移与时间的关系可表示为[4-5]:

(2)

(3)

式中，gt0为t= 0时的重力加速度，此时位移x=x0；gx0为x=0处的重力加速度，gt0=gx0+γx0；地表重力梯度γ≈3.086 μGal/cm。

由于重力梯度和光速有限性等因素可通过相关公式进行改正，因此选用式(1)对自由落体重力加速度的精度展开详细讨论。忽略时间测量噪声，并假设位移测量噪声εxi(噪声来源主要包括落体棱镜振动、激光干涉信号测量电路和地脉动对参考棱镜的影响等)为零均值随机白噪声，E(εxi)=0，则测量位移信号可表示为:

(4)

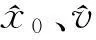
(5)

(6)

此时重力加速度的估计值可表示为:

(7)

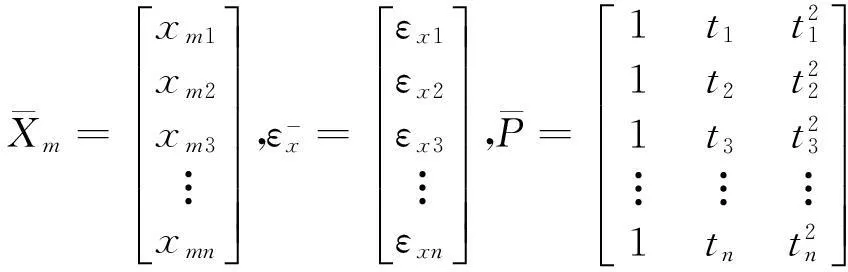
根据误差理论，对估计矩阵进行协方差计算[6]:

(8)

(9)

(10)

2　两种数据处理模式的对比分析

2.1等时间间隔

等时间间隔采样是在相同的时间间隔Δt触发系统对位移信号xi的采集。自由落体的总时间为T，则第i次落体的时间为ti=i·Δt。当采集点数n较大时，在计算中忽略小量，则等时间间隔协方差矩阵的极限值为:

(11)

2.2等距离间隔

(12)

2.3两种模式的对比分析

表1　参数拟合精度与误差因子的极限值

对于等时间间隔和等距离间隔两种模式而言，各误差因子都是随着数据点数n的增加而减小，且各误差因子的极限值γCLS与精确值γN随着点数n的增加而更接近。

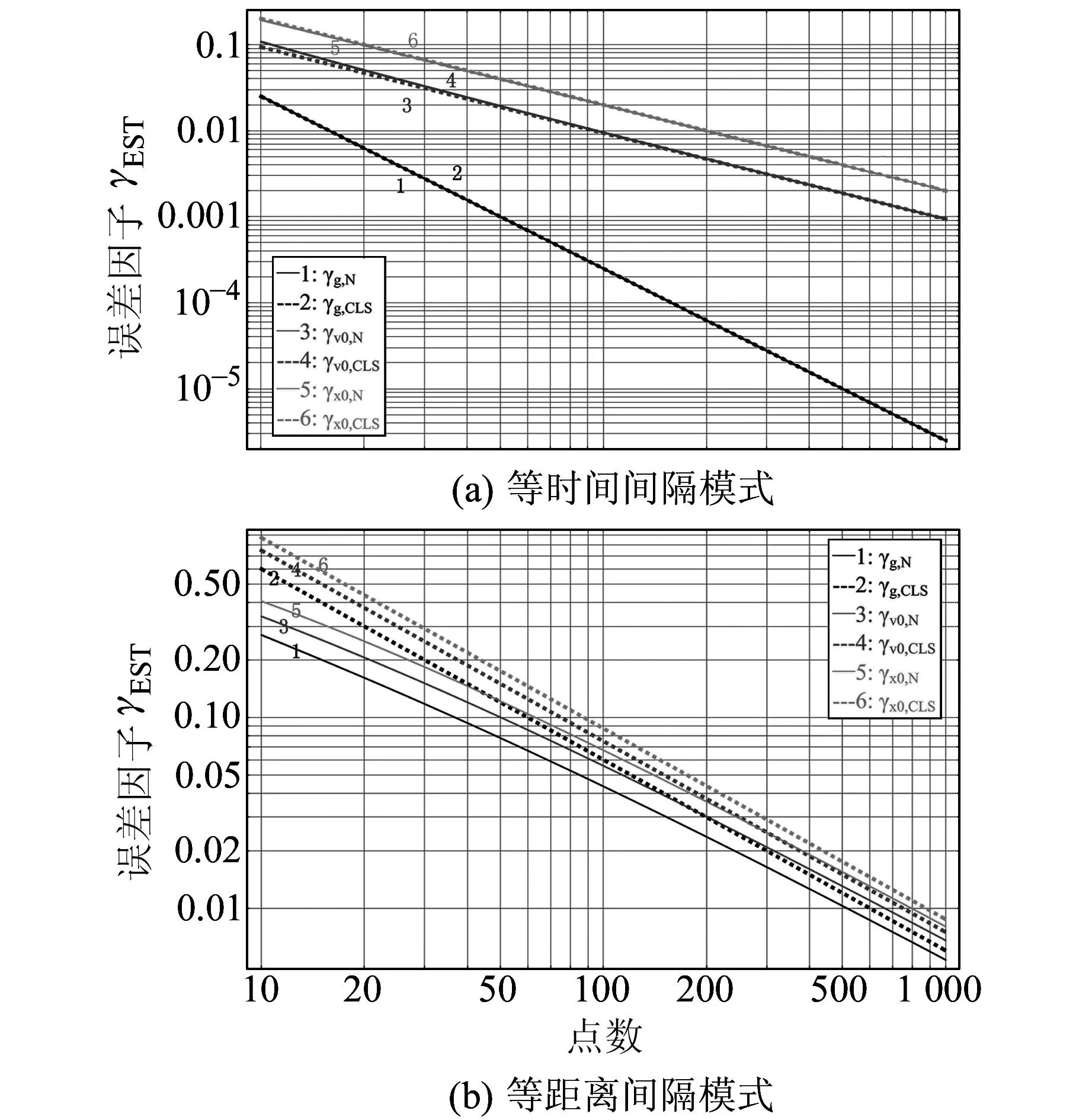
图1　等时间间隔与等距离间隔两种模式下误差因子随点数n的变化Fig.1　Relative error factors’ variation due to the number n for both equally spaced in time and equally spaced in distance

2.4重力值精度随各参数的变化

假设自由落体高度为0.2 m，落体时间为0.2 s，干涉激光波长为633 nm，且位移测量噪声的方差为σx=1 nm。

针对同样的落体高度，取不同的干涉条纹分频数对应不同数量的数据点，分频数越高得到的采集点越少。若使用所有数据进行拟合，重力值方差随分频数的变化曲线如图2所示。随着分频数的增加，得到的数据量随之减小，重力值的拟合方差增加；在相同的分频条件下，初始速度v0增加也会导致g值拟合精度的恶化。

2.4.2等距离间隔重力值拟合数据段选取

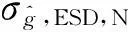
图2　重力值精度随干涉条纹分频数和初始速度v0的变化Fig.2　Standard error of the gravity due to different interference fringe scale and initial velocity v0

若固定第1 000点作为终止，重力值精度随起始点的变化曲线如图4所示。此时重力值精度在起始点取100左右时达到最优，约小于1 μGal，且起始最优点将随着初始速度v0的增减而后移。若固定第1点作为起始，同样得到重力值方差随终止点的变化曲线如图5所示。此时重力值方差在终止点取900左右时最优，约1 μGal，且终止最优点将随着初始速度v0的增减而后移。

图3　数据长度固定时重力值精度随数据段的变化Fig.3　Standard error of the gravity due to different data segment of which the length is fixed

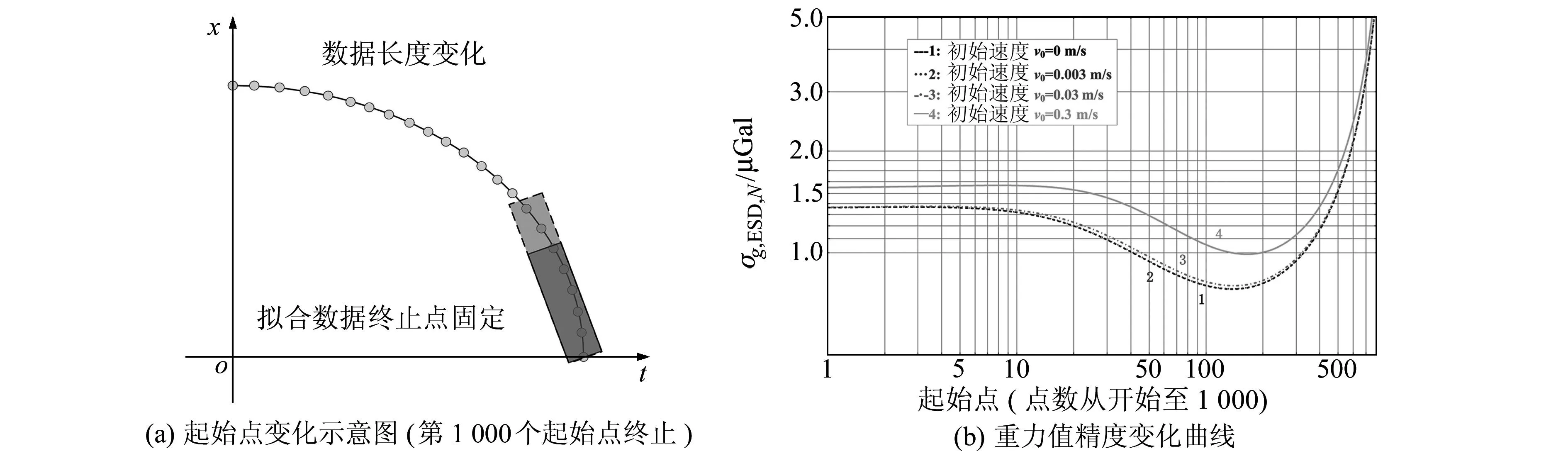
图4　重力值精度随数据起始点的变化(第1 000个点固定为终止点)Fig.4　Standard error of the gravity due to different data segment of which the stop point is fixed(1 000th point is set as the end)

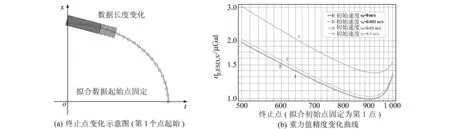
图5　重力值精度随数据终止点的变化(第1个点固定为起始点)Fig.5　Standard error of the gravity due to different data segment of which the start point is fixed(1st point is set as the beginning)

综上所述，为提高等距离间隔模式下重力值的精度，需要尽可能地减小自由落体的初始速度v0，并合理增加自由落体中偏后的数据段来进行参数拟合。等时间间隔模式也能得出类似的结论。

3　结　语

1)重力仪测量g值的精度极限值与测量时间的平方和测量点数的平方根成反比；

2)在位移测量噪声为白噪声的前提下，重力值拟合精度随分频数的增加(等效落体测量点数的减小)和初始速度的降低而提高；

3)合理选择数据段来进行参数拟合，能优化重力值精度。

参考文献

[1]Zumberge M A. A Portable Apparatus for Absolute Measurements of the Earth’s Gravity[D]. Boulder:University of Colorado, 1981

[2]Svetlov S M. An Absolute Gravimeter and Vibration Disturbances: A Frequency Responses Method[A]//Gravity, Geoid and Marine Geodesy[M]. Berlin Heidelberg: Springer,1997[3]Nagornyi V D. A New Approach to Absolute Gravimeter Analysis[J]. Metrologia, 1995, 32(3): 201-208

[4]Niebauer T M, Sasagawa G S, Faller J E,et al. A New Generation of Absolute Gravimeters[J]. Metrologia, 1995, 32(3): 159-180

[5]Orlob M. Spectral Analysis of Synthetically Affected FG5 Absolute Gravimeter Residuals[D]. Dallas:University of Texas, 2011

[6]费业泰. 误差理论与数据处理[M]. 北京：机械工业出版社, 2000 (Fei Yetai. Error Theory and Data Processing[M]. Beijing: China Machine Press, 2000)

Foundation support:National Key Scientific Instrument and Equipment Development Project, No.ZDYZ2012-1-04; National Natural Science Foundation of China, No.41504140.

About the first author:HU Ming, PhD, assistant researcher , majors in inertial sensor and gravimeter, E-mail: huming@whigg.ac.cn.

收稿日期：2015-09-11

第一作者简介：胡明，博士，助理研究员，主要从事惯性传感器与重力仪相关研究，E-mail：huming@whigg.ac.cn。

DOI：10.14075/j.jgg.2016.08.009

文章编号：1671-5942(2016)08-0694-04

中图分类号：P312

文献标识码：A

Optimization of the Standard Deviation of the Estimated Gravity Acceleration in the Free Fall Absolute Gravimeter

HUMing1ZHANGWeimin1TIANWei1ZHONGMin1

1State Key Laboratory of Geodesy and Earth’s Dynamics,Institute of Geodesy and Geophysics, CAS,340 Xudong Street, Wuhan 430077, China

Abstract:We show the asymptotical expressions for equal space in time (EST) and equal space in distance (ESD), in order to estimate the standard deviation of the parameters of the initial position, the initial velocity and the gravity acceleration. We then discuss the variation of the standard deviation of the gravity acceleration, caused by fringe scales, initial velocity and data segment. By increasing the scales, reducing the initial velocity and selecting the suitable data segment, we give the optimization method for obtaining a minimal value of the standard deviation of the gravity acceleration.

Key words:absolute gravimeter; free fall; data segment; equal space in time; equal space in distance

项目来源：国家重大科研装备研制项目(ZDYZ2012-1-04)；国家自然科学基金(41504140)。