一种适用于精密单点定位的抗差自适应滤波

陈泉余　隋立芬　刘乾坤　王凌轩　曾　添

1　信息工程大学地理空间信息学院，郑州市科学大道62号，450001



一种适用于精密单点定位的抗差自适应滤波

陈泉余1隋立芬1刘乾坤1王凌轩1曾添1

1信息工程大学地理空间信息学院，郑州市科学大道62号，450001

摘要：分析了卫星星座PDOP值与卫星数的关系以及伪距和载波相位观测值残差量级的大小，结合精密单点定位各参数的特性，提出一种适用于精密单点定位的分类因子抗差自适应滤波法。该方法在等价权函数的选取上兼顾PDOP值的检验，并对不同观测量分别进行抗差等价权替换。根据不同参数的特性，建立分类自适应因子，利用预测残差求取各类参数的自适应因子。实验表明，该方法不仅能检测和控制异常观测量对定位解算的影响，而且能提高PPP定位的精度及可靠性。

关键词：精密单点定位；自适应滤波；抗差滤波；自适应因子

目前，IGS能够为用户提供包含精密星历、精密钟差、差分码偏差等各种高精度产品，为用户实现高精度PPP提供了必要条件[1]。针对PPP预处理、误差改正、残差检验3个处理阶段，已有许多有效方法提出，如周跳探测[2]、模型精化[3]、递推DIA方法[4]等。对于异常观测值的处理，一般通过构造检验统计量来检测和判定。虽然各阶段都有相应手段对异常值加以控制，降低其对定位的影响，但一些未能探测到的异常值仍会对参数估计以及随机模型产生偏差。特别是在单系统PPP下，可用卫星数不多时，将严重影响定位的精度及可靠性。

抗差自适应滤波能够有效抑制观测异常误差和动力学模型误差的影响[4-5]。本文在此基础上，针对精密单点定位中各类参数和观测值的特性以及观测星座的空间几何结构，提出一种适用于精密单点定位的抗差自适应滤波算法，并用MGEX跟踪站的观测数据进行验证。

1　PPP函数模型及Kalman滤波解

PPP定位通常采用伪距和相位组合，构造无电离层组合观测值[6]，其表达式为：

(1)

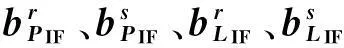
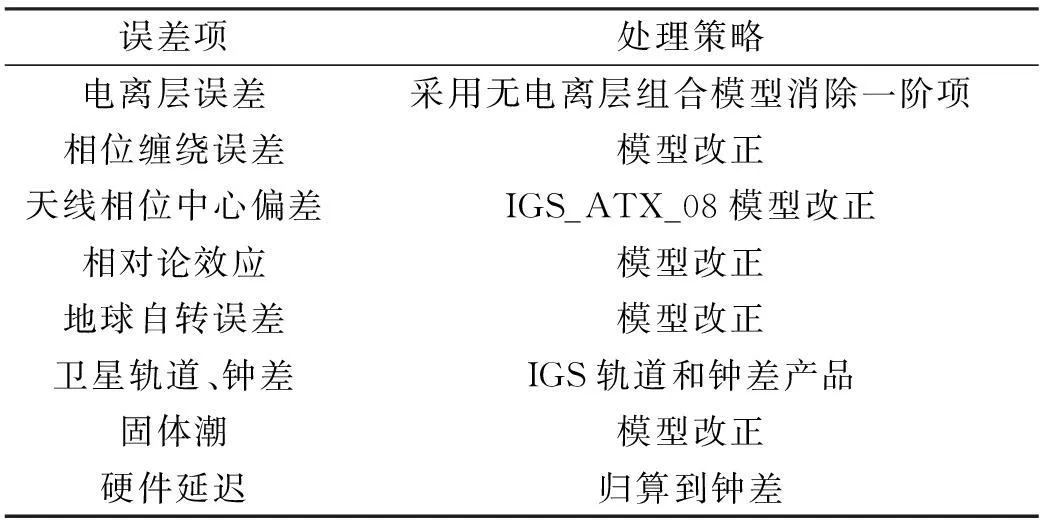
表1　误差处理策略

观测方程经线性化，得：

(2)

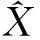
(3)

(4)

(5)

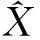
PPP定位的状态方程为：

(6)

式中，Φk,k-1为从tk-1时刻到tk时刻的状态转移矩阵，Wk为系统噪声向量，ΣWk为系统噪声的协方差阵。其中,

(7)

首次定位时，位置参数通常采用伪距单点定位结果，其精度一般为m级，此时位置参数的方差设置为104m2。由于接收机钟差和模糊度参数的先验信息是未知的，故将其初始值设为0，同时给定一个较大的方差，通常也设为104m2。对流层延迟可以通过模型改正，因此将模型改正的值设为对流层延迟的初始值。由于模型改正的精度相对于其他参数高，因此其初始方差通常设为10-2m2。完成首次定位后，系统噪声的方差及其参数值可以由上一历元获取。由此可以得到PPP定位Kalman滤波解的递推形式[4]：

(8)

2　抗差自适应滤波

2.1抗差自适应滤波解

PPP待估参数通常包括接收机位置、接收机钟差、天顶对流层延迟和无电离层组合模糊度。这些待估参数各有不同的特性，处理方法也不尽相同。位置参数是时不变参数(静态PPP)，其过程噪声通常设为0；接收机钟差参数的随机模型是高斯白噪声；对流层延迟变化较为缓慢，通常采用随机游走过程；在无周跳情况下，模糊度的值为时不变参数，系统过程噪声也通常设为0，当周跳发生时将重新初始化。由于位置参数、接收机钟差、对流层延迟和模糊度参数属于不同类型的参数，很难采用统一的自适应因子进行调节，可对不同的分量选取不同的自适应因子。分类因子抗差自适应滤波解为：

(9)

(10)

PPP定位采用伪距和相位观测值，而这两种观测值的观测精度不同，其残差值的大小也不同(图1)。在没有异常值的情况下，无电离层组合相位残差值为-0.02m～0.02m，而组合伪距的残差值变化范围为-4.0m～4.0m，伪距残差明显比相位残差大2个量级左右。因此，在观测值等价权和自适应因子的解算上，应将这两类观测值区别对待。

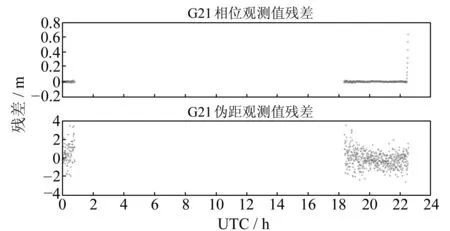
图1　JFNG 测站G21号卫星的残差值Fig.1　G21 satellite’s residual values at JFNG station

2.2等价权的选取

等价权函数主要有丹麦法权函数、Huber权函数[7]以及IGG系列权函数[7-8]。等价权函数的选取对于异常值的控制以及定位精度和可靠性有直接关系，应结合PPP定位的实际来选定。

PDOP值反映的是卫星几何强度。卫星几何结构与卫星数密切相关，卫星数越多，卫星几何强度越大，PDOP值就越小[9]。如果PDOP值过大且超过设定的阈值，该历元的观测数据则作为异常观测处理，不执行定位解算。而在执行抗差等价权替换时，若某颗卫星观测值存在较大异常，则将这颗卫星置为不可用(观测值的权为0)，从而使得PDOP发生较大跳变，导致PDOP检验量不能通过。为避免这种情况，应选取较为合适的等价权函数。

图2给出了MGEX跟踪站CUT0在各观测时刻的可用卫星数以及所有可用卫星和删除1颗可用卫星时的PDOP值。由图可知，测站CUT0可用的GPS卫星数并不多，通常只有7～8颗，而较差时刻仅有5颗。删除1颗可用卫星时，PDOP值会发生明显跳变。而在观测时刻仅有5颗可用卫星时，如果将其中1颗置为不可用，则不能执行正常的定位解算。鉴于这种情况，在等价权选取时需同时考虑卫星的几何结构和观测值异常。本文采用Huber权函数[7]：

(11)

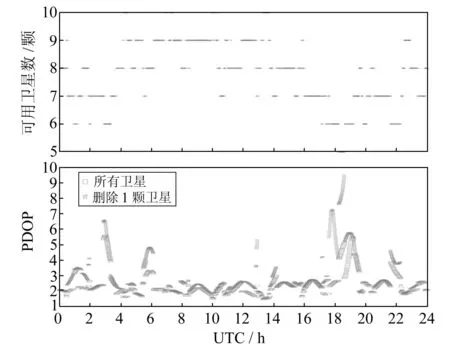
图2　CUT0测站的可用卫星数及PDOP值Fig.2　Available satellite number and PDOP valueat CUT0 station

2.3自适应因子的确定

自适应因子的求取通常需要先构造误差判别统计量。误差判别统计量有状态不符值统计量[10]、预测残差统计量[11]、基于观测信息与动力学模型预测信息的方差分量统计和速度不符值统计量[12]。自适应因子的计算有三段函数、两段函数、指数函数和选权函数模型[13]。利用预测残差统计量构造自适应因子，不需要在滤波前计算预测向量的参考值，也不需要观测个数大于状态参数个数。同时，在精密单点定位模型中未知参数个数较多，多余观测数较少，如果采用最小二乘方法计算状态不符值，则不能够很好地检测出异常值。本文采用预测残差统计量和三段函数模型来确定自适应因子[14]：

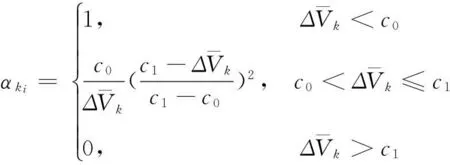
(12)

(13)

(14)

3　实验结果及分析

为了验证该方法的可行性，从静态PPP和动态PPP两个方面进行算例分析。由于实验条件有限，本文采用仿动态PPP来替代动态PPP。实验采用两种滤波方案进行定位：方案1，Kalman滤波；方案2，抗差自适应滤波。

3.1静态PPP分析

以MGEX跟踪站JFNG2015年年积日123d的GPS静态观测数据为例，数据采样间隔为30s。解算过程中发现,该数据的观测质量较差，虽然预处理阶段已采取必要的控制措施，但仍然存在未被检测的异常观测量。定位结果与IGS发布的坐标偏差如图3所示。

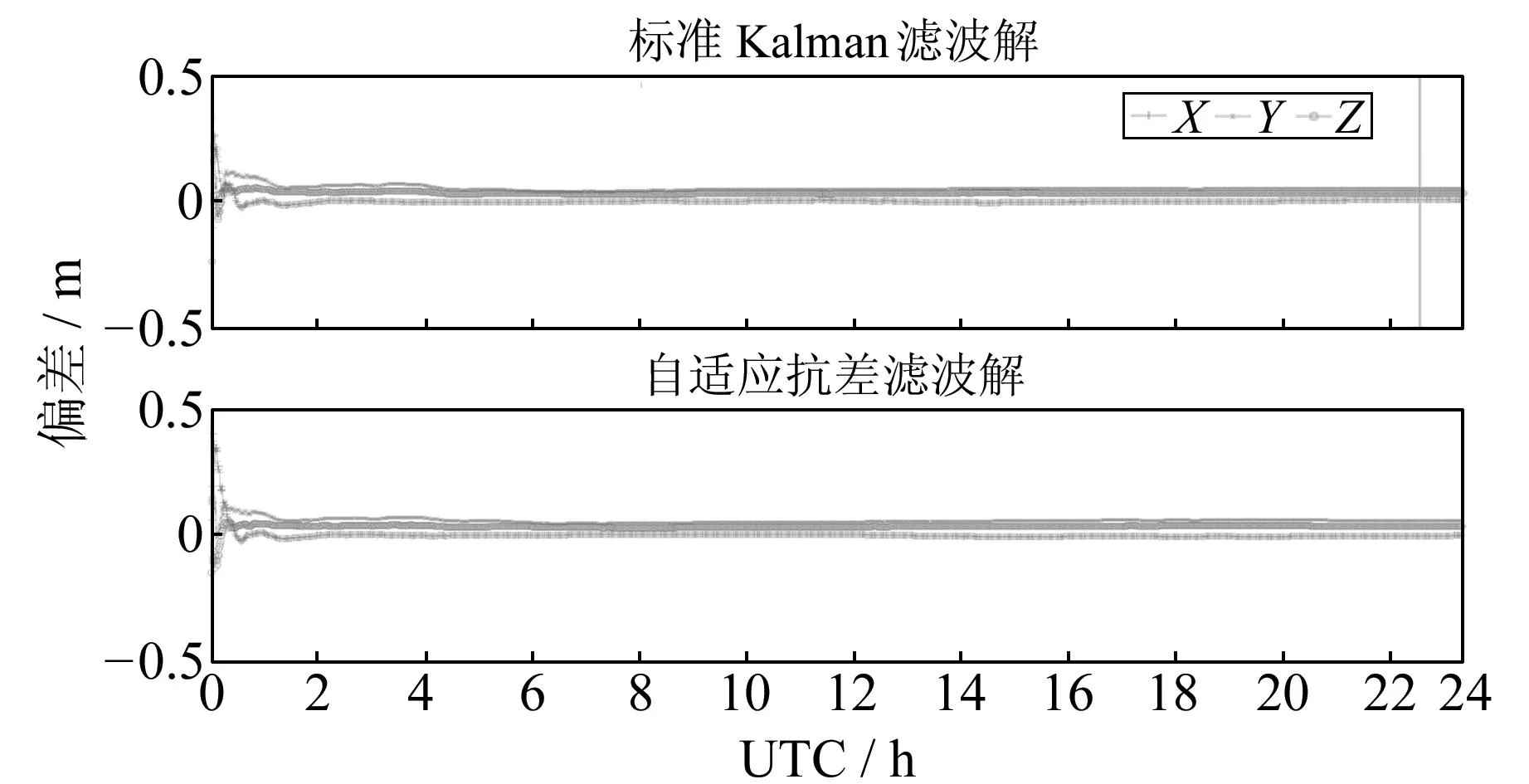
图3　JFNG测站静态PPP两种滤波结果Fig.3　The static of two filtering results at JFNG station

1)在没有异常观测值的影响下,两种滤波方法有较好的吻合性，且满足高精度定位的需求。

2)在定位收敛阶段，方案2要优于方案1。这是因为在观测前期接收机还不稳定，给观测值造成了一定的干扰；或者是由于各处理阶段的异常控制将含有异常值的卫星观测量直接剔除，改变了观测值的空间几何结构，造成方差阵不合理。

3)在观测时刻UTC22:31:30～22:32:00，方案1的定位结果发生明显跳变，定位偏差大到数十m甚至上百m。这是由于存在异常观测值，而异常观测值有可能是不敏感周跳组合或其他难以探测的检验量。由图1的残差值可以看出，在该时刻载波相位的残差值发生显著跳变。

4)方案2明显具有抵制或削弱异常观测值影响的能力。虽然在滤波各阶段都进行了相应的质量控制以抵制异常观测值的影响，但仍然存在一些不能检测的异常值。方案2能够很好地解决此类问题。

为验证方法的有效性，选取9个MGEX跟踪站第123d全天观测数据进行静态PPP测试，分别采用两种滤波方案进行解算。以IGS发布的坐标作为真值，计算两种方案定位偏差的均方根误差(RMS)，如图4。

由图4 可知，除MAYG、NKLG、PTGG3个测站外，方案2的定位偏差较方案1都有明显提升，其中JFNG和SEYG提升最为显著。虽然MAYG、NKLG和PTGG的定位精度方案1较方案2好，但两种方案定位偏差的差别并不大。这可能是由于观测噪声或者多路径等误差过大，影响了观测值等价权替换或者权因子。但总体来说，方案2较方案1为优。

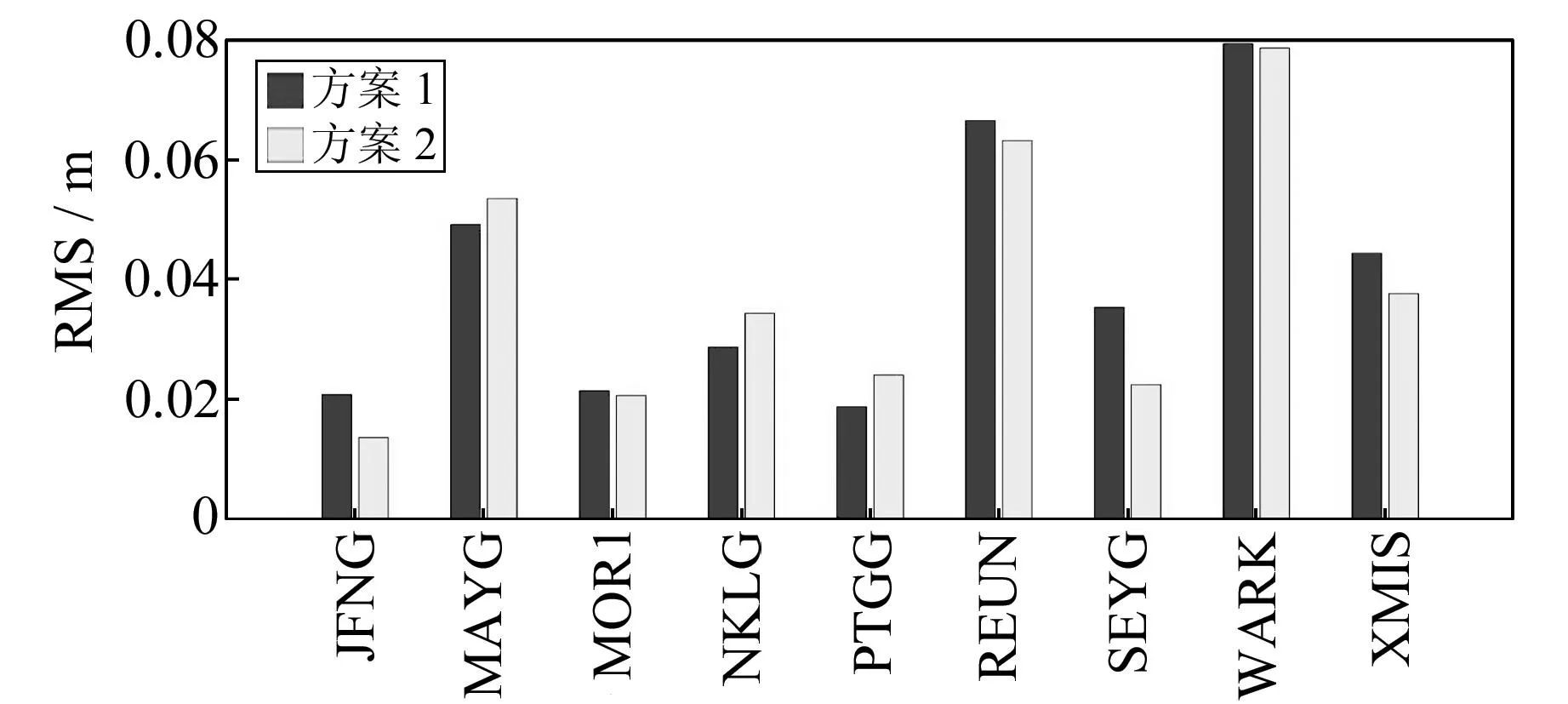
图4　两种滤波方案对应的静态PPP定位RMSFig.4　The static PPP of two filtering results RMS

3.2仿动态PPP分析

类似地，采用仿动态处理NKLG跟踪站2015年年积日123d的GPS静态观测数据，采样间隔为30s。同样采用两种滤波方案进行验证，定位结果与IGS坐标偏差如图5所示。

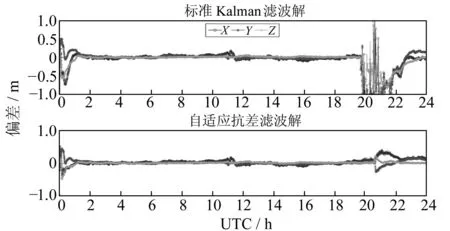
图5　NKLG测站仿动态两种滤波结果Fig.5　The Imitation dynamic of two filtering results at NKLG station

由图5可知，由于受残留误差和周跳等因素的影响，方案1解算的定位结果在观测时刻UTC19:41:30～22:28:00发生剧烈跳动，定位偏差达到m级，并且历元间的偏差变化剧烈。而从方案2的解算结果来看，虽然在相应观测时段内也发生跳变，但其跳变范围较方案1小，跳变值大小仅为0.4m，较方案1有明显改善。在这一时段，由于方案2重置了模糊度值，需要一定的重新收敛时间，收敛后仍具有较高的定位精度。

此外，为了验证方案2的有效性，还选取了8个MGEX跟踪站第123d全天观测数据进行仿动态PPP测试。分别采用两种滤波方案进行解算，以IGS发布的坐标作为真值，计算收敛后两种方案的平均均方根误差(RMS)，见图6和表2。可见，方案2的精度较方案1有显著提升，其中WARK、XMIS的改善程度最为明显，分别达到13.78%和10.92%，8个测站的平均改善幅度达到6.66%。

图6　两种滤波方案对应的仿动态PPP定位的RMSFig.6　Two filtering schemes corresponding to the dynamic PPP positioning of the RMS

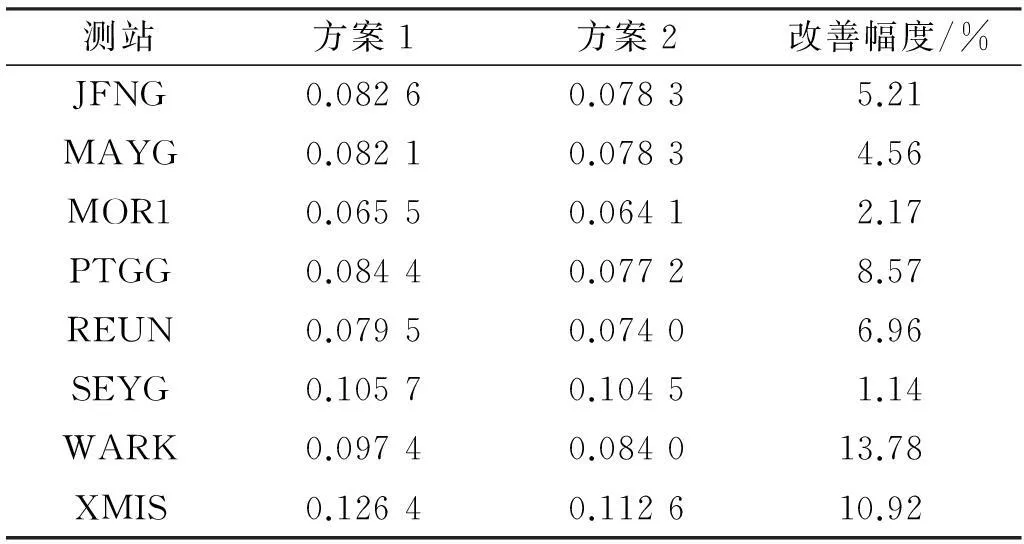
测站方案1方案2改善幅度/%JFNG0.08260.07835.21MAYG0.08210.07834.56MOR10.06550.06412.17PTGG0.08440.07728.57REUN0.07950.07406.96SEYG0.10570.10451.14WARK0.09740.084013.78XMIS0.12640.112610.92

4　结　语

本文提出一种分类抗差自适应滤波算法，能够顾及PPP定位中的观测值异常和动力学模型异常。实验表明，该方案不仅能够处理观测值异常和动力学模型异常，而且能够改善定位的精度及可靠性。

参考文献

[1]李征航，黄劲松．GPS测量与数据处理[M]．武汉：武汉大学出版社，2010(Li Zhenghang，Huang Jinsong．GPS Surveying and Data Processing[M]．Wuhan：Wuhan University Press，2010)

[2]方荣新，施闯，魏娜，等．GPS数据质量控制中的实时周跳探测研究[J]．武汉大学学报：信息科学版，2009，34(9)：1 094-1 097(Fang Rongxin，Shi Chuang，Wei Na，et al．Real-Time Cycle-Slip Detection for Quality Control of GPS Measurements[J]．Geomatics and Information Science of Wuhan University，2009，34(9)：1 094-1 097)

[3]何海波．高精度GPS动态测量及质量控制[D]．郑州：信息工程大学，2012 (He Haibo．Precise Kinematic GPS Surveying and Quality Control[D]．Zhengzhou: Information Engineering University，2012)

[4]杨元喜．自适应动态导航定位[M]．北京：测绘出版社，2006(Yang Yuanxi．Adaptive Navigation and Kinematic Positioning[M]．Beijing：Surveying and Mapping Press，2006)

[5]杨元喜，任夏，许艳．自适应抗差滤波理论及应用的主要进展[J]．导航定位学报，2013，1(1)：9-15(Yang Yuanxi，Ren Xia，Xu Yan．Main Progress Adaptively Robust Filter with Applications in Navigation[J].Journal of Navigation and Positioning，2013，1(1) ：9-15)

[6]肖国锐．BDS精密单点定位技术研究及软件实现[D]．郑州：信息工程大学，2014(Xiao Guorui. Theoretical Research and Program Implementation of Beidou Navigation Satellite System Precise Point Positioning[D]．Zhengzhou: Information Engineering University，2014)

[7]杨元喜．抗差估计理论及其应用[M]，北京：八一出版，1993(Yang Yuanxi．Robust Estimation Theory and Its Applications[M].Beijing:Bayi Press，1993)

[8]周江文．经典误差理论与抗差估计[J]．测绘学报，1989(2)：115-120(Zhou Jiangwen．Classical Theory of Errors and Robust Estimation[j]．Acta Geodatica et Cartographica Sinica，1989(2)：115-120)

[9]宋超．精密单点定位快速收敛技术与方法研究[D]．郑州：信息工程大学，2015(Song Chao. Technologies and Methods on Rapid Convergence of Precise Point Positioning[D]．Zhengzhou: Information Engineering University，2015)

[10]Yang Y，He H，Xu G．Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]．Journal of Geodesy，2001，75(2)：109-116

[11]徐天河，杨元喜．改进的Sage自适应滤波方法[J]．测绘科学，2000，25(3)：22-24(Xu Tianhe，Yang Yuanxi．The Improved Method of Sage Adaptive Filtering[J]．Science of Surveying and Mapping，2000，25(3)：22-24)

[12]Yang Y，Xu T．An Adaptive Kalman Filter Based on Sage Windowing Weights and Variance Components[J]．The Journal of Navigation，2003，56(2)：231-240

[13]Yang Y，Gao W．Influence Comparison of Adaptive Factors on Navigation Results[J]．The Journal of Navigation，2005，58(3)：471-478

[14]崔先强，杨元喜．分类因子自适应抗差滤波[J]．自然科学进展，2006，16 ( 4 )：490-494(Cui Xianqiang，Yang Yuanxi．Classification Factor Adaptive Filtering [J]．Progress in Natural Science，2006，16 ( 4 )：490-494)

Foundation support:National Natural Science Foundation of China，No.41274016，41174006，40974010；Open Fund of State Key Laboratory of Geographic Information Engineering，No.SKLGIE2013-M-2-1.

About the first author:CHEN Quanyu, postgraduate, majors in GNSS data processing，E-mail:cqy_xd@163.com.

收稿日期：2015-09-07

第一作者简介：陈泉余，硕士生，主要研究方向为GNSS数据处理，E-mail:cqy_xd@163.com。 通讯作者：隋立芬，教授，博士生导师，主要从事空间大地测量数据处理理论与方法研究，E-mail:suilifen@163.com。

DOI：10.14075/j.jgg.2016.08.017

文章编号：1671-5942(2016)08-0732-05

中图分类号：P228

文献标识码：A

Corresponding author:SUI Lifen, professor, PhD supervisor, majors in spatial geodetic data processing, E-mail:suilifen@163.com.

Robust Adaptive Filtering for Precise Point Positioning

CHENQuanyu1SUILifen1LIUQiankun1WANGLingxuan1ZENGTian1

1School of Surveying and Mapping, Information Engineering University,62 Kexue Road,Zhengzhou 450001,China

Abstract:We discuss the relationship between the PDOP value of satellite constellation and satellite number and analyze the magnitudes of the residual errors of pseudo-range and carrier phase observations value. We propose a classification factor robust adaptive filtering method. This method is applied for precise point positioning and the equivalent replacement is based on observation of the different values. At the same time, the adaptive factor is set up according to the characteristics of different parameters and calculated by the prediction residual. Experiments show that this method can not only detect and control the influence of the abnormal values, but can also improve the accuracy and reliability of PPP.

Key words:precise point positioning (PPP); adaptive filtering; robust filtering; adaptive factor

项目来源：国家自然科学基金(41274016,41174006,40974010)；地理信息工程国家重点实验室开放基金(SKLGIE2013-M-2-1)。