水准仪磁致误差检定的测量不确定度分析

赵立军　李文一　程增杰　苏国营　张　晶

1　中国地震局第一监测中心，天津市耐火路7号，300180



水准仪磁致误差检定的测量不确定度分析

赵立军1李文一1程增杰1苏国营1张晶1

1中国地震局第一监测中心，天津市耐火路7号，300180

摘要：通过对由亥姆赫兹线圈和测微平行光管构成的水准仪磁致误差检定装置的测量方法及其不确定度来源的分析，讨论了水准仪磁致误差检定的测量不确定度的评估方法，阐述了检定结果不确定度主要由测量重复性、测微平行光管的刻划误差和读数误差、磁场以及磁致误差特性曲线拟合引入。对这些分量分别进行分析与公式推导，最终评定出检定装置的扩展不确定度。

关键词：磁致误差检定；不确定度；曲线拟合

不确定度是表征被测量值分散性的重要参数。对于计量工作来说，实际检测过程不可避免地受到各种因素的影响，对测量结果进行不确定度分析，对测量、实验结果的可信性、可比性和可接受性有着重要影响[1-4]。对于具有补偿器的自动安平水准仪[5]，其补偿摆在磁场作用下可能会偏离垂线位置，从而带来高程观测值误差，称为磁致误差。大量实验表明，精密水准测量中的磁致误差是不可忽视的[6-7]。为此，中国地震局第一监测中心建造了国内领先的水准仪磁致误差检定实验室，依据检定规程对置于亥姆赫兹线圈匀强磁场中的水准仪的目镜橫丝偏移量进行测量，以计算出仪器的磁致误差[8]。对此方法下水准仪磁致误差检定的测量不确定度进行分析评定，是评价该装置测量水平、判定测量结果质量的重要手段。

本文对磁致误差检定装置的不确定度来源进行分析，包括测量重复性、测微平行光管的刻划误差和读数误差、磁场以及磁致误差特性曲线拟合等，评估各参数的标准不确定度，推导实际检定曲线拟合中引入的不确定度分量的计算公式，最终针对具体检定过程评定出合成标准不确定度和扩展不确定度。

1　各不确定度分量的分析与评定方法

1.1测量重复性引入的不确定度

该项不确定度来源主要包括测量装置受外界干扰(振动、温度变化)、平行光管测微器读数重复性以及被测水准仪十字丝的安平重复性等。对这些来源综合考虑，采用A类标准评定不确定度。

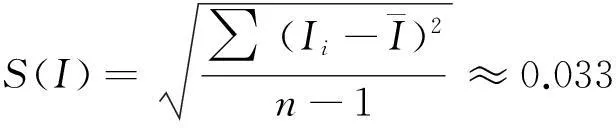
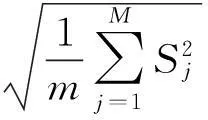
1.2测微目镜刻划误差引入的不确定度

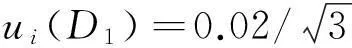
1.3读数误差引入的不确定度

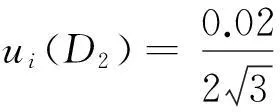
1.4磁致误差特性曲线拟合引入的不确定度

由于在检定过程中每台仪器均需利用不同磁场下观测得到的十字丝偏差拟合磁场-磁致误差关系曲线，再通过曲线求得该仪器在1倍地磁场下(60 μT)的十字丝偏差作为检定结果，因此必然要针对每台仪器曲线拟合引入的测量不确定度，给出该分量的计算公式。根据规程需要，分别在0～600 μT磁场中均布的7个磁场强度下测量仪器的十字丝偏差量，共测两个测回(即每个场强测量4组数据)，并利用最小二乘曲线拟合出磁场-磁致误差关系曲线。

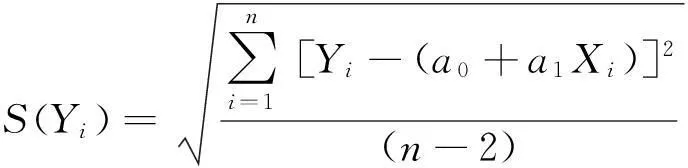
(1)

式中，n表示测量次数(2个测回、7个点，n取28)。

1.5磁场条件的不确定度

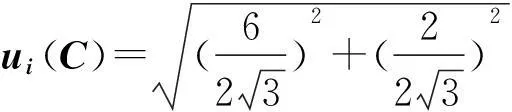
假设磁致误差-磁场关系曲线方程为X=b0+b1Y，其中X表示磁致误差测量值，Y表示对应的磁场大小，则磁场条件不准确所引起的磁致误差测量结果不确定度分量为：

(2)

2　磁致误差检定的测量不确定度评定及其报告

根据上述方法对TRIMBLE公司生产的一台DiNi12型电子水准仪的磁致误差检定结果进行不确定度评定。该水准仪精度等级为DSZ05级，测量数据如表1所示。

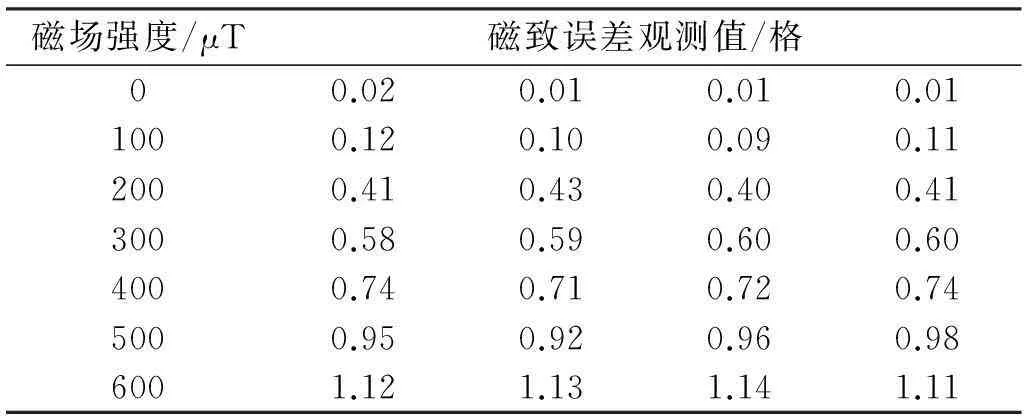
表1　磁致误差测量数据

1)考虑每个十字丝偏移量均需2次读数(施加磁场与不施加磁场所读值相减即为十字丝偏移量)，因此读数所引起的测量不确定度在合成时系数为2。

2)利用最小二乘法可以拟合出磁场强度-磁致误差关系曲线为Y=10.789 5+526.315 8X。根据式(1)，当Y0=60 μT(即1倍地磁场)时，残余标准差为：

由拟合曲线引入的测量不确定度分量为：

3)根据测量数据拟合得到的磁致误差-磁场强度关系曲线方程为X=0.001 9Y-0.020 5，由式(2)可以计算出磁场条件不准确所引起的磁致误差测量结果不确定度分量ui(M)=b0+b1ui(C)=0.001 9×1.826-0.020 5≈-0.017(格)。

4)最终合成标准不确定度u(合)=

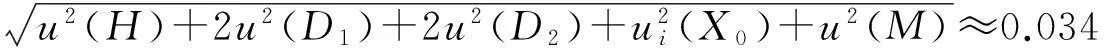
取包含因子k=2，可得扩展不确定度U=0.01″。

3　结　语

磁致误差检定装置的不确定度来源包括测量重复性、测微平行光管的刻划误差和读数误差、磁场以及磁致误差特性曲线拟合等。本文评估了各参数的标准不确定度，推导出实际检定曲线拟合过程中引入的不确定度分量的计算公式，并针对具体检定过程进行不确定度的评定，最终评定出的扩展不确定度U=0.01″(k=2)。参考《JJG 425-2003 水准仪检定规程》中对DSZ05级水准仪的限差要求为0.06″，可以对该装置下测量结果的可信性和可接受性作出肯定。

从评定过程来看，曲线拟合过程中会引入一定的不确定度，同时该不确定度与具体测量数据有着很大的关系。因此，凡是运用到曲线拟合得到测量结果的过程，必须考虑拟合引入的不确定度，并在实际工作中对曲线拟合的各因素进行严格控制，尽量减少测量结果的不确定度，提高测量质量。

参考文献

[1]国家质量技术监督局．JJG 1059.1-2012测量不确定度评定与表示[S]．北京：中国计量出版社，2012(State Bureau of Technology Supervision. JJG l059.1-2012 Evaluation and Expression of Uncertainty in Measurement[S]. Beijing: Chinese Metrology Press,2012)

[2]国家质量技术监督局计量司.测量不确定度评定与表示指南[M].北京:中国计量出版社,2000(Department of Metrology, State Bureau of Technology Supervision.Guidelines for the Evaluation and Presentation of Uncertainty in Measurement[M]. Beijing: Chinese Metrology Press, 2000)

[3]何文森. 实验中的不确定度估算[J]. 实验科学与技术，2012, 10(3): 19-21(He Wensen. Calculation of Uncertainty in Experiment[J]. Experiment Science and Technology, 2012, 10(3): 19-21)

[4]汤绯，黄绣娟. 测量不确定度评定及实例分析[J].环境科学与管理，2012, 37(5): 135-139(Tang Fei，Huang Xiujuan. Evaluation of Measurement Uncertainty and Case Study[J].Environmental Science and Management,2012, 37(5): 135-139)

[5]国家技术监督局.JJG 425-2003水准仪检定规程[S].北京:中国计量出版社,2003(State Bureau of Technology Supervision. JJG 425-2003 Verification Regulationof Levels[S]. Beijing: Chinese Metrology Press,2003)

[6]任道胜.精密补偿器水准仪磁致误差及其测试方法[J].地壳形变与地震,1997,17(4): 67-72(Ren Daosheng.Magnetic Error of Precise Compensator Level and Its Test Method[J].Crustal Deformation and Earthquake,1997,17(4): 67-72)[7]彭沛民.对国家标准GB12897-91部分条款的修改建议[J].地壳形变与地震, 1996,16(2):85-89(Peng Peimin. Proposals of Some Amendments for the State Standard of GB12897-91[J].Crustal Deformation and Earthquake,1996,16(2):85-89)

[8]董炽.磁场对Ni002水准仪影响的实验[J].地壳形变与地震,1987,7(3): 240-246(Dong Chi. A Experiment on the Effect of Magnetic Field upon Ni002 Leveler[J].Crustal Deformation and Earthquake,1987,7(3): 240-246)

[9]Thijsse B J, Rust B W. Freestyle Data Fitting and Global Temperatures[J]. Computing in Science & Engineering, 2008, 10(1):49-59

[10]Jin Y, Yue H, Brown M, et al. Improving Data Fitting of a Signal Transduction Model by Global Sensitivity Analysis[C]. American Control Conference, New York， 2007

[11]Penna M A, Dines K A. A Simple Method for Fitting Sphere-Like Surfaces[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2007, 29(9):1 673-1 678

Foundation support:Science and Technology Innovation Fund of the First Crust Monitoring and Application Center, CEA,No.FMC2014004.

About the first author:ZHAO Lijun, assistant engineer, majors in the metrology and measuring techniques and instruments,E-mail:zhaolijun5618@163.com.

收稿日期：2015-08-03

第一作者简介：赵立军,助理工程师,研究方向为测试计量技术及仪器，E-mail:zhaolijun5618@163.com。

DOI：10.14075/j.jgg.2016.08.021

文章编号：1671-5942(2016)08-0750-03

中图分类号：P242

文献标识码：A

Evaluation of Measurement Uncertainty for Magnetic Error Calibration of Levels

ZHAOLijun1LIWenyi1CHENGZengjie1SUGuoying1ZHANGJing1

1First Crust Monitoring and Application Center, CEA, 7 Naihuo Road, Tianjin 300180, China

Abstract:This paper is concerned with analysis of the measurement of the magnetic error calibration of levels and the relevant sources of uncertainty. We analyze the evaluation method of uncertainty for magnetic error calibration of levels. The sources of the uncertainty result from the reproducibility of measurement, the ruling error of micrometer collimator, the reading error, the magnetic field and the fitted linear regression equation for the calibration curve; these sources of uncertaintyare discussed and calculated. The combined standard uncertainty and expanded uncertainty are reported. The results show that the fitted linear regression equation for the calibration curve is an important source of uncertainty.

Key words:calibration of magnetic error; uncertainty; curve fitting

项目来源：中国地震局第一监测中心科技创新主任基金(FMC2014004)。