基于多元整体最小二乘优化的多点灰色动态变形分析模型

吴开岩　张献州　马　龙　罗　烈　张　拯　喻　巧

1　西南交通大学地球科学与环境工程学院，成都市犀安路999号，610031　2　高速铁路运营安全空间信息技术国家地方联合工程实验室，成都市犀安路999号，610031　3　中铁二院工程集团有限责任公司，成都市通锦路3号，610031　4　铁道第三勘察设计院集团有限公司，天津市中山路10号，300142



基于多元整体最小二乘优化的多点灰色动态变形分析模型

吴开岩1,2张献州1,2马龙1,2罗烈1,2张拯3喻巧4

1西南交通大学地球科学与环境工程学院，成都市犀安路999号，6100312高速铁路运营安全空间信息技术国家地方联合工程实验室，成都市犀安路999号，6100313中铁二院工程集团有限责任公司，成都市通锦路3号，6100314铁道第三勘察设计院集团有限公司，天津市中山路10号，300142

摘要：提出一种多元整体最小二乘优化的多点灰色动态模型,并结合实例验证优化的MGM(1,n)模型的优越性。将优化的MGM(1,n)模型与一般的MGM(1,n)模型进行对比,分析两种模型的建模值和预测值。结果表明，优化的MGM(1,n)模型在建模数据多于4期的情况下建模精度更高，预测精度更准确,更符合实际情况。

关键词：多元整体最小二乘法； 多点动态灰色模型； 变形分析； 灰色预测

变形的分析与预报是变形监测的主要内容，其方法主要有BP神经网络、回归分析、灰色模型、时间序列等[1]。这些方法大多是单点分析方法。但在同一监测网中,不同监测点之间存在着某种联系,这些监测点之间相互影响。显然，在对这些监测点进行数据分析时将某一监测点剥离出来单独分析是不可靠的,而是应将多个监测点统一建模进行分析。因此,在变形监测分析与预报中,使用多点灰色动态模型更为合理。多点灰色动态模型(MGM(1,n))是GM(1,1)模型在多点情况下进行拓展后得到的[2]。目前，多点灰色动态模型的优化主要是针对背景值[3-4]以及残差项[5-6]，这些优化模型都取得了很好的效果。但在多点灰色动态模型建模过程中,使用了最小二乘法(LS)对发展系数A和灰色作用量B进行求解。只有在误差均值为0且只存在于观测向量中时,最小二乘法求得的解才是无偏最优解。多点灰色动态模型在建模过程中,观测值和背景值都是直接由观测数据或通过简单计算得到的。因此，观测矩阵和背景值矩阵中都含有一定的误差或扰动,这时使用LS法所求得的估计参数是有偏的。多元整体最小二乘法是在整体最小二乘法基础上进行拓展后得到的[7-9],将整体最小二乘法中的参数向量和观测向量拓展为参数矩阵和观测矩阵，并在计算过程中同时顾及观测矩阵和参数矩阵中的误差。因此，本文提出了基于多元整体最小二乘优化的多点灰色动态变形分析模型。实验证明，该模型可以抑制模拟数据误差并提高预测数据的精度。

1　MGM(1,n)模型

设某变形体有n个相互关联的变形监测点,对变形体进行观测获得m期变形观测数据,其相应的变形观测序列为:

其一次累加序列为：

由单点灰色预测模型的一阶微分方程式扩展成MGM(1,n)模型的一阶微分方程：

(1)

写成矩阵形式为：

(2)

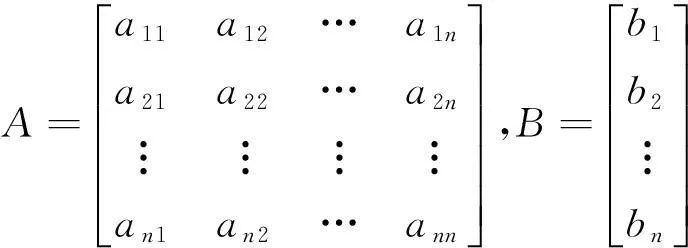
上述微分方程的解(即时间响应函数)为：

(3)

式(3)即为MGM(1,n)模型的一般形式,式中参数A与B通过最小二乘求得。

2　优化的MGM(1,n)模型研究

2.1多元整体最小二乘模型

多元整体最小二乘法(MTLS)在整体最小二乘法(TLS)基础上进行拓展。对于超定线性方程组Y=Ax,在整体最小二乘中Y和x分别是n×1的观测向量和m×1的参数向量,而多元整体最小二乘中Y和x则是n×d的观测矩阵和m×d的参数矩阵。

将Y=Ax改写成：

(4)

式中,Y、EY∈Rn×d分别为观测矩阵和观测矩阵残差阵,A、EA∈Rm×n分别为系数矩阵和系数矩阵残差阵,Ξ∈Rm×d为未知参数阵。MTLS与TLS有相同的约束准则,即F范最小：

vec(EY)T·vec(EY)+vec(EA)T·vec(EA)

(5)

式中，vec(•)为矩阵列向量化算子,tr表示矩阵的迹。

在等权条件下,MTLS的解法可分为SVD法和拉格朗日乘数法,本文使用拉格朗日乘数法对MTLS进行求解[7-8]。式(4)的拉格朗日目标函数可以表示为：

(6)

式中,λ为拉格朗日乘常数。由拉格朗日乘数法的必要条件，最终可得到：

(7)

(8)

可通过迭代求得MTLS的最终解。迭代过程如下。

1)通过最小二乘法求得Ξ的初值,即

(9)

(10)

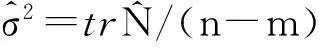
2.2优化的MGM(1,n)建模方法

1)根据式(1)～(3)建立多点动态灰色模型时间响应式；

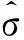
3)求解时间响应式；

5)精度评定。

3　模型实验与分析

为了比较传统的MGM(1,n)模型与优化后的MGM(1,n)模型之间的数据模拟和预测效果,使用文献[3]中京哈公路(G102线)长春至德惠某路段中同一断面上3个点位移计所测的12期监测数据，其中前8期数据序列用于建模，后4期数据序列用于检测预测值的准确性。

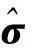
通过表1、表2可以看出：

1)在建模精度方面,传统的MGM(1,n)模型和优化的MGM(1,n)模型都能够较好地模拟出建模数据,但优化的MGM(1,n)模型精度明显高于传统的MGM(1,n)模型。

2)在预测精度方面, 传统MGM(1,n)模型的平均相对误差较大,不能较好地预测数据的变化情况；而优化的MGM(1,n)模型平均相对误差较小,能够较好地预测出未来数据的变化情况。参考模型精度等级[1],传统的MGM(1,n)为2级,优化的MGM(1,n)为1级，也证明了本文对多点灰色动态模型的改进是正确可行的。

3)点位移计所产生的观测值受到温度、电缆长度等因素的影响，在观测值中会含有少量的误差。因此，在MGM(1,n)的建模过程中，观测矩阵和背景值矩阵都含有少量的误差。本文实验证明，在系数矩阵和观测矩阵同时存在一定的扰动时,用LS法求出的解并不是最优解。

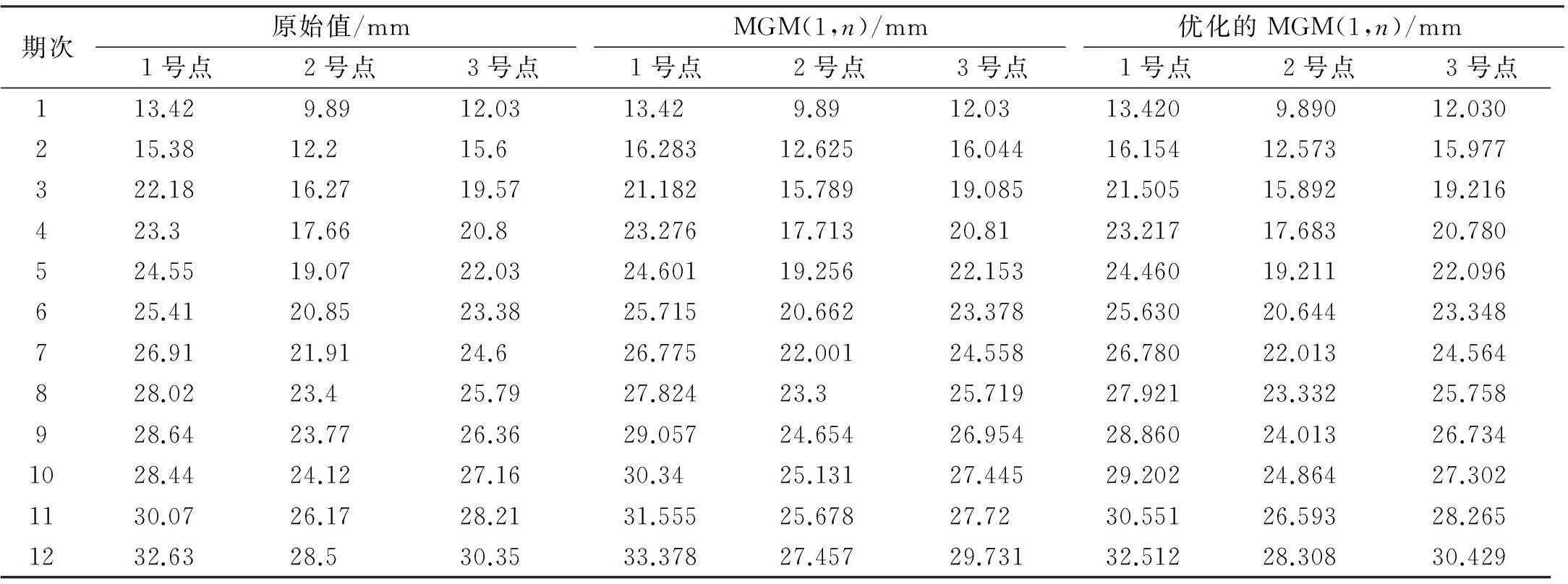
表1　原始值与两种模型建模结果

表2　模型精度评定

4　结　语

本文使用京哈公路(G102线)长春至德惠某路段中同一断面上3个点位移计所测的监测数据,分别对传统的MGM(1,n)模型和优化的MGM(1,n)模型进行建模分析,研究优化的MGM(1,n)模型在实际精密工程测量中的实用性和可靠性。

1)本文模型是在传统的MGM(1,n)模型基础上进行一定的优化,顾及系数阵和观测阵中同时含有一定的扰动,使用多元整体最小二乘法代替传统的MGM(1,n)模型中的最小二乘法，对发展系数A和灰色作用量B进行求解。实验证明了此模型的可靠性。

2)当观测数据存在一定的扰动时,优化的MGM(1,n)模型的建模精度和预测精度高于传统的MGM(1,n)模型。此模型具有一定的实用性,可以为精密工程测量的预测提供一定的参考。

研究发现,优化的MGM(1,n)模型在建模数据只有3或4期的情况下,容易出现建模失败的情况。这是由于在使用多元整体最小二乘进行求解的过程中，建模数据太少可能会出现矩阵A秩亏或者SVD分解过程中矩阵块V22奇异[7-9],使得迭代求解不收敛，导致建模失败。因此，优化的MGM(1,n)模型在整体适用性上不如传统的MGM(1,n)模型。此外,本文只是以实验验证了优化的MGM(1,n)模型在建模精度和预测精度上要高于传统的MGM(1,n)模型,如何从理论上推导还需进一步探讨。

参考文献

[1]黄声享,尹辉,蒋征,等.变形监测数据处理[M].武汉:武汉大学出版社,2003 (Huang Shengxiang,Yin Hui, Jiang Zheng,et al. Deformation Monitoring Data Processing [M].Wuhan：Wuhan University Press,2003)

[2]潘国荣,王穗辉.多点变形动态灰色模型辨识及预测[J]. 测绘学报,2002,31(S1):66-69(Pan Guorong, Wang Suihui. Dynamic Grey Modelling Identification and Predication of Multi-point Deformation [J].Acta Geodaeticaet et Cartographica Sinica, 2002, 31(S1):66-69 )

[3]刘寒冰,向一鸣,阮有兴. 背景值优化的多变量灰色模型在路基沉降预测中的应用[J]. 岩土力学,2013,34(1):173-181(Liu Hanbing, Xiang Yiming, RuanYouxing. A Multivariable Grey Model Based on Background Value Optimization and Its Application to Subgrade Settlement Prediction[J].Rock and Soil Mechanics,2013, 34(1):173-181)

[4]李玻,蒋艳,杨秀文,等.优化背景值的灰色MGM(1,n)模型[J]. 西南大学学报:自然科学版,2013,35(1):89-94(Li Bo, Jiang Yan, Yang Xiuwen, et al. MGM(1,n) Model of Optimized Background[J].Journal of Southwest University:Natural Science Edition, 2013, 35(1):89-94)

[5]陈西江,鲁铁定.残差自适应回归MGM(1,n)[J]. 测绘科学,2012,37(2):36-37(Chen Xijiang, Lu Tieding. MGM(1,n) Based on Adaptive Regression of Residual[J]. Science of Surveying and Mapping,2012,27(2):36-37)

[6]李晓蕾,刘睿,田永瑞,等. 基于灰色预测的空间多点残差修正模型研究[J]. 大地测量与地球动力学,2010,30(5):125-128(Li Xiaolei, Liu Rui, Tian Yongrui,et al.Study on Spatial Multi-Point Residual Model[J].Journal of Geodesy and Geodynamics, 2010, 30(5):125-128)

[7]Schaffrin B, Felus Y A. On the Multivariate Total Least-Squares Approach to Empirical Coordinate Transformations: Three Algorithms[J]. J Geod，2008，82(6):373-383

[8]Felus Y A, Burtch R C. On Symmetrical Three-Dimensional Datum Conversion[J]. GPS Solutions, 2009, 13(1): 65-74[9]Schaffrin B, Felus Y A. Multivariate Total Least-Squares Adjustment for Empirical Affine Transformations[C]. The 6th Hotine-Marussi Symposium for Theoretical and Computational Geodesy, Berlin, 2007

[10] 刘经南,曾文宪,徐培亮. 整体最小二乘估计的研究进展[J]. 武汉大学学报:信息科学版,2013,38(5):505-512(Liu Jingnan, Zeng Wenxian, Xu Peiliang. Overview of Total Least Methods[J].Geomatics and Information Science of Wuhan University, 2013,38(5):505-512)

[11] 冯健,花向红,王刘准. 整体最小二乘的GM(1,n)模型在高铁中的应用研究[J]. 测绘地理信息,2014,39(1):64-66(Feng Jian, Hua Xianghong, Wang Liuzhun. Application of GM(1,n) Model in High-Speed Rail[J]. Journal of Geomatics, 2013, 39(1):505-512)

[12] 明祖涛,刘军,夏力,等. 改进的灰色模型在高铁沉降预测中的应用[J]. 测绘科学,2015,40(4):137-140(Ming Zutao, Liu Jun, Xia Li,et al. Study of the Implementation of Improved Grey Model in High-Speed Railway Settlement Prediction[J]. Science of Surveying and Mapping, 2015,40(4):137-140)

Foundationsupport:NationalNaturalScienceFoundationofChina,No.41374002;ScienceandTechnologyProjectofSichuanProvince,No.2015JQ0046;ProgramforChangjiangScholarsandInnovativeResearchTeaminUniversity,No.IRT13092.

Aboutthefirstauthor:WUKaiyan,postgraduate,majorsinprecisionengineeringsurvey,E-mail:wky781249@qq.com.

收稿日期：2015-09-19

第一作者简介：吴开岩，硕士生，主要从事精密工程测量及变形监测研究，E-mail：wky781249@qq.com。

DOI：10.14075/j.jgg.2016.08.006

文章编号：1671-5942(2016)08-0682-04

中图分类号：P258

文献标识码：A

A Multivariable Grey Deformation Analysis Model Based on Multivariate Total Least-Squares Optimization

WUKaiyan1, 2ZHANGXianzhou1, 2MALong1, 2LUOLie1, 2ZHANGZheng3YUQiao4

1FacultyofGeosciencesandEnvironmentalEngineering,SouthwestJiaotongUniversity, 999Xi’anRoad,Chengdu610031,China2State-ProvinceJointEngineeringLaboratoryofSpatialInformationTechnologyforHigh-SpeedRailwaySafety,999Xi’anRoad,Chengdu610031,China3ChinaRailwayEryuanEngineeringGroupCoLtd, 3TongjinRoad,Chengdu610031,China4TheThirdRailwaySurveyandDesignInstituteGroupCorporation,10ZhongshanRoad,Tianjin300142,China

Abstract:In the process of deformation analysis, it is more reasonable and reliable that multiple monitoring points are applied to modeling and analyzing of grey system in the same deformation monitoring network compared with single monitoring point. But the traditional multivariable grey model (MGM(1,n)) has some short comings. This paper proposes a multivariable grey model based on multivariate total least-squares optimization. And the superiority of this model is proved by some examples. Simultaneously, comparing this model with the traditional MGM(1,n) and analyzing the modeling value and predictive value of these two models. The results show that the modeling and prediction accuracy of this model are higher than MGM(1,n) and this model is more suitable for the actual circumstances when the number of data modeling is over four. This model can be referred to the analysis and forecast of deformation monitoring data in further research.

Key words:multivariate total least-squares; multivariable grey model; deformation analysis; grey prediction

项目来源：国家自然科学基金(41374002)；四川省科技项目(2015JQ0046)；长江学者和创新团队发展计划(IRT13092)。