例析自主定义型问题的求解

◇ 北京 丁益祥(特级教师)

例析自主定义型问题的求解

◇ 北京 丁益祥(特级教师)

自主定义型问题是指根据问题的设计需要,人为地定义某个概念、某种运算、某条规则等等,并要求按照这些自主定义的概念、运算、规则处理的问题.因此,读懂并理解这些概念、运算、规则的定义,对于解决这类问题起着至关重要的作用.

1 自主定义新概念问题

例1 设S为复数集C的非空子集,若对任意x、y∈S,都有x＋y,x－y,xy∈S,则称S为封闭集.现给出下列命题:

①集合S＝{a＋bi|a、b为整数,i为虚数单位}为封闭集;

②若S为封闭集,则一定有0∈S;

③封闭集一定是无限集;

④若S为封闭集,则满足S⊆T⊆C的任意集合T也是封闭集

其中所有真命题的序号是________.

按照题目中给出的定义,如果复数集C的一个非空子集S是封闭集,那么,必须满足对于S中的任意2个数,它们的和、差、积仍是S中的数.因此,要完成题目中4个命题真假的判断,必须依据封闭集的概念,逐一审视.

对于命题①,∀x、y∈S,不妨设x＝a1＋b1i, y＝a2＋b2i,且a1、b1、a2、b2都是整数,则

由于a1、b1、a2、b2都是整数,所以a1±a2,b1± b2,a1a2－b1b2,a1b2＋a2b1都是整数,所以x＋y∈S,x－y∈S,xy∈S,因此①正确.

对于命题②,∀x、y∈S,由于S为封闭集,所以x－y∈S.取x＝y,得0∈S,因此②正确.

对于命题③,若集合S＝{0},显然S满足封闭集定义中的所有条件,所以S是封闭集.但S是有限集,因此③错误.

对于命题④,取S＝{0},T＝{0,1},满足S⊆ T⊆C.但由于0－1＝－1∉T,故T不是封闭集,因此④错误.

综上所述,真命题是①、②.

例2 设[x]表示不超过x的最大整数(如[2]＝2,[5/4]＝1),对于给定的n∈N∗,定义＝则当x∈ [3/2,3)时,函数的值域是________.

上述2个问题,都是自主定义新概念问题.例1自主定义了封闭集的概念.正确理解封闭集的意义,明确封闭集中元素的基本特征,并据此逐一分析所给命题,是解决问题的基本方法.例2自主定义了一个新函数将命题视角聚焦在对新函数符号的阅读和理解上.同时,着意考查了函数的单调性及其值域、考查了阅读理解能力、自主学习能力以及分类与整合的思想.由于符号“”与组合记号“”有着相同的结构形式,极易弄混,因此,此题对思辨意识也有着较高的要求.

自主定义新概念是自主定义型问题中的典型问题之一,求解这类问题,关键在于对自主定义的新概念的阅读和理解.

2 自主定义新运算问题

例3 定义一种运算“⊗”:当m,n都是正奇数或都是正偶数时,m⊗n＝m＋n;当m,n一个是正奇数另一个是正偶数时,m⊗n＝mn.则集合M＝{(a,b)| a⊗b＝36,a、b∈N∗}中元素的个数是( ).

A 21; B 26; C 31; D 41

当a、b都是正奇数或都是正偶数时,a⊗b＝

36＝1＋35＝2＋34＝…＝34＋2＝35＋1,有35个(a,b);

当a、b一个是正奇数另一个是正偶数时,a⊗b＝1×36＝3×12＝4×9＝9×4＝12×3＝36×1,有6个(a,b).

综上,集合M中共有41个元素.选D.例4 任意2个非零平面向量α和β,定义α◦β＝若平面向量a、b满足|a|≥|b|＞0,a与b的夹角且a◦b、b◦a都在集合{n/2|n∈Z}中,则a◦b＝( ).

A 1/2; B 1; C 3/2; D 5/2

由定义,得

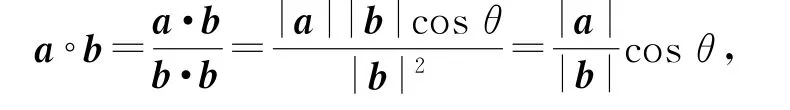
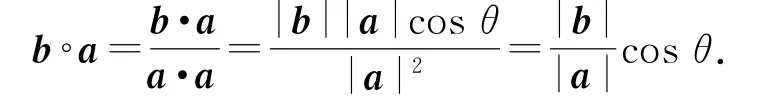
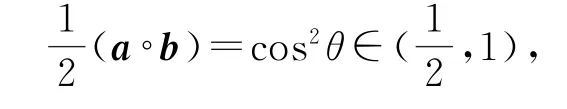
所以(a◦b)∈(1,2).而(a◦b)∈{n/2|n∈Z},所以a◦.因此选C.

上述2个问题,都是自主定义新运算问题.例3的求解,应分正整数m、n奇偶性相同或奇偶性相异2种情况,并按题目中关于“⊗”的不同定义分别进行运算.例4自主定义了2个非零向量α和β之间的一种运算“◦”,读懂这种运算的意义,并注意运算结果所在集合中元素的特征以及三角函数的有界性,是解决问题的关键.

自主定义新运算问题,通常会对所给出的运算符号赋予明确的意义,并给出与之“等价”的常规意义下的算式.处理这类问题,一般只需把给出的算式当作公式或法则使用,即可快速获解.

3 自主定义新规则问题

例5 为绿化环境,某地区大面积植树造林,在区域{(x,y)|x≥0,y≥0}内植树(如图1).第1棵树在A1(0,1)点,第2棵树在B1(1,1)点,第3棵树在C1(1,0)点,第4棵树在C2(2,0)点,接着按图中箭头方向每隔一个单位种2棵树,那么第2016棵树所在的点的坐标是( ).

A (8,45);

B (9,45);

C (8,44);

D (9,44)

观察图中各正方形右上角顶点处所植树的序号以及方向,不难发现,正方形对角线OB1所在直线上的点(1,1)处种植第1×2棵树,点(2,2)处种植第2×3棵树,点(3,3)处种植第3×4棵树,……,点(n,n)处种第n(n＋1)棵树.并且,当n是奇数时,由该顶点出发的箭头方向向下,当n为偶数时,由该顶点出发的箭头方向向左.

由此只需确定满足不等式n1(n1＋1)≤2016≤n2(n2＋1)的正整数n1或n2即可.

因为44×45＝1980＜2016＜2070＝45×46,所以与第2016棵树对应点的纵坐标为44.

又2016－1980＝36,所以第2016棵树所对应点的横坐标为44－36＝8.因此,第2016棵树所在的点的坐标是(8,44).

例6 甲、乙2人做报数游戏,游戏的规则是:2人从1开始轮流连续报数,第一个报数的人1必须报,每人一次至少报1个数,最多可以连续报7个数,并且前一个人报完数后,后一个人必须接着前一个人所报的最后一个数往后依次连续报数.例如:前一个人报数“1,2”,则后一个人可以有“3”,“3,4”,…,“3,4, 5,6,7,8,9”共7种报数方法.规则约定,谁先报出“100”谁获胜.现从甲开始报数,若甲要想必胜,则甲第一次报出的数应该是________.逆过来想.由于规则约定每人一次至少报1个数,最多可以连续报7个数,因此,若甲想下一次能报出100,则甲前一次报出的最后一个数必须是92.这样,乙虽可以有“93”,“93,94”,…,“93,94, 95,96,97,98,99”共7种报法,但此时,甲只需对应报“94,95,96,97,98,99,100”,“95,96,97,98,99,100”,…,“100”,即可获胜.

如此看来,当乙报m(1≤m≤7)个数时,甲只需报8－m个数,就可以抢先报出“100”.这是一个首项为100,公差为－8的等差数列问题.易知,甲只需逐次抢先报出92,84,76,…,4,即可获胜.因此,甲要想必胜,第一次报出的数应该是“1,2,3,4”.

上述2个问题,都是自主定义新规则问题.例5规定了植树的初始位置、株距间隔以及走势.求解此题我们从2个不同角度进行了分析.分析1由正方形对角线上点的坐标特征与该点处所植的树的序号之间的关系切入,通过直观抽象和适当的计算快速地解决了问题.分析2通过与平方数的联想,结合株距间隔以及箭头走势分析,也不难获得正确的结果.例6规定了报数游戏的规则以及获胜的标准,通过逆向思维,利用倒推的方法,把问题转化成了等差数列问题来求解.

从以上2个问题的处理过程,我们清晰地看到,问题给出的规则是定律,只要我们真正理解问题提出的规则,并且坚决遵照执行,那么问题必将迎刃而解.

自主定义型问题在近年的数学高考中有着较高的考查频率,读懂自主定义的概念、法则、运算或规则,并能真正理解和掌握,是解决这类问题的关键.为此,我们既要重视课本中现成的概念、法则、运算或规则的学习和应用,又要善于从所给的材料中,学习领悟或抽象概括出课本中没有的新的概念、法则、运算或规则,进而达到利用新概念、新运算、新规则解决“从未见过的”新问题的目的.

北京陈经纶中学)