3D打印系统执行机构仿真分析*

余　轩，郑银环

(武汉理工大学机电工程学院，湖北武汉430070)



3D打印系统执行机构仿真分析*

余轩，郑银环

(武汉理工大学机电工程学院，湖北武汉430070)

执行机构是3D打印系统的关键部件，它可以影响系统的运动精度和稳定性。建立了执行机构的三维模型，在ADAMS中完成执行机构的运动学仿真，并利用ADAMS和ANSYS建立刚柔耦合动力学模型，分析模型的振动情况。结果表明，执行机构在正常工作状态下满足精度要求和稳定性要求，为进一步强化执行机构的性能提供了措施。

3D打印系统执行机构刚柔耦合动力学模型运动学仿真

0　引言

自3D打印技术问世以来，3D打印机便成为3D技术领域的前瞻性产品。3D打印机作为一种高科技设备，综合应用了CAD、CAM等科学技术，在研发中能够快捷方便地获得三维实物模型，方便后期的优化设计。执行机构作为3D打印系统的关键部件，其精度是保证产品加工精度的基础，性能优劣直接关系到3D打印系统的精度和稳定性。采用ADAMS对执行机构进行运动学仿真，确保其机构设计正确。同时运用ANSYS和ADAMS建立执行机构的刚柔耦合动力学模型，在ADAMS软件中完成悬臂梁系统的动力学仿真，校验执行机构模拟实际工况下系统的最大振动位移值，使设计结果满足精度要求，获得系统最大振动位移值的位置，对结构进行优化。

1　3D打印系统执行机构三维模型的建立

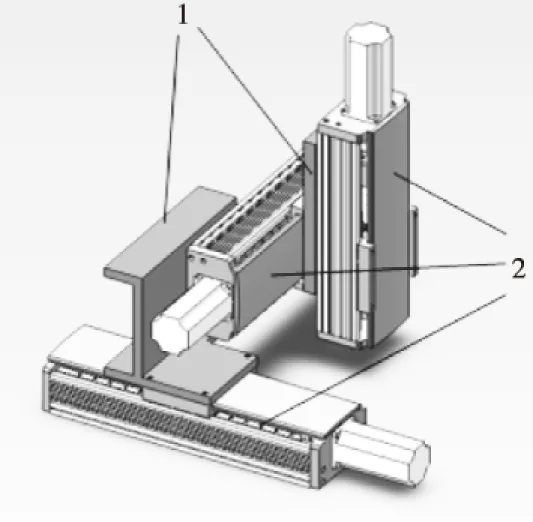
1-连接板；2-伺服滑台　图1　悬臂梁式结构示意图

3D打印系统执行机构的结构不同，对系统的精度和稳定性影响也不一样。执行机构主要有三种结构形式，分别是悬臂梁式、龙门式和一体式结构[1-2]。本文对3D打印系统的工作精度、工作目标以及打印喷头空间运动范围等进行综合分析，选用悬臂梁式执行机构。悬臂梁式结构比较稳定，精度可以达到0.01 mm，工作空间较龙门式和一体式大，三轴滑台均由伺服电机驱动，各个滑台之间运动灵活。根据执行机构各零件的结构尺寸和装配要求，在SolidWorks中完成3D打印系统执行机构的建模。3D打印系统执行机构由三个伺服滑台(X、Y和Z轴滑台)以及X、Y轴连接板组成，X轴连接板将X、Y轴的伺服滑台装配连接在一起，Y轴连接板则连接Y轴与Z轴滑台。运用SolidWorks软件完成三个伺服滑台的虚拟装配，装配后如图1所示。

2　执行机构的运动学仿真分析

将简化的三维模型导入ADAMS软件中，利用虚拟样机技术对其进行仿真，完成执行机构运动学分析，查看各部件的运动情况，检查各零部件干涉情况。

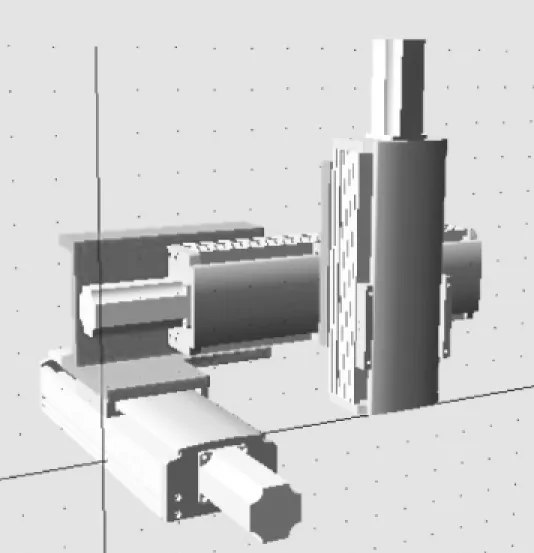
图2　执行机构导入模型

执行机构的零部件数目有93个，如果全部导入到ADAMS中，则在添加约束时工作量会很大，而且容易选不上零件或选错零件。因此在导入装配体之前有必要对模型做简化处理。本文主要完成执行机构的运动学仿真，查看滑块沿各伺服滑台的运动情况，对于滑台内部的零件可以不必导入。以此作为简化依据，简化执行机构三维模型，简化后的模型中有20个零件，包括有X、Y和Z轴各自的U型基座、顶盖、基座侧盖、电机和运动滑块，以及X轴连接板和Y轴连接板等。导入模型如图2所示。

对所有零件添加约束，定义材料属性并检查约束添加是否正确。为了客观实际地反应执行机构中三个伺服滑台的运动情况，可以对运动部件添加位移函数，如STEP、IF函数，完成在虚拟样机中模拟执行机构工作中的运动轨迹，检查各滑台运动时是否存在干涉和碰撞现象，以及能否满足行程要求。

STEP函数的使用格式为：STEP(x，x0，h0，x1，h1)

其中：x是自变量，通常为时间或者时间的任意函数；x0为STEP函数自变量的初始值；x1为STEP函数自变量的结束值；h0为STEP函数的初始值；h1为STEP函数的最终值。函数值为常数、设计变量或其它函数表达，其函数值的定义给STEP函数可以使用多层嵌套的功能，常见的多层嵌套方式为：STEP(x,x0,h0,x1,(STEP(x,x1,h1,x2,(STEP(x,x2,h2,x3,h3)))))。

IF函数的使用格式为：IF(x1:x2,x3,x4)。其中，x1为判断条件，若x1<0，则返回x2；若x1=0，则返回x3；若x1>0，则返回x4。

执行机构某一工作段内X轴滑块的运动情况是：运动滑块处于伺服滑台某一位置，先沿着滑台向底端(定义滑台电机端为顶端，非电机端为底端)以0.2 mm/s的速度运动0.45 s，在0.45 s至0.55 s内减速至零，运动滑块位于滑台底端附近；在0.55 s至0.65 s内反方向加速至0.2 mm/s ，再匀速运动0.9 s后在0.1 s内减速为零，此时滑块位于滑台顶端附近；再次反方向(滑块往底端移动)加速0.1 s至速度为0.2 mm/s，后匀速运动0.45 s回到初始运动位置。

嵌套使用IF函数和STEP函数，编写运动步骤程序。查看X轴滑块仿真运动情况，得到滑块的位移与速度曲线图，如图3所示。ADAMS软件默认的坐标与执行机构滑台坐标不一致，X轴滑台位于ADAMS软件三维坐标的Z轴上、Y轴滑台位于ADAMS软件三维坐标的X轴上、Z轴滑台位于ADAMS软件三维坐标的Y轴上，仿真曲线图中显示为ADAMS中的坐标。为了查看仿真结果，分别分析伺服滑台中运动滑块的运动情况。

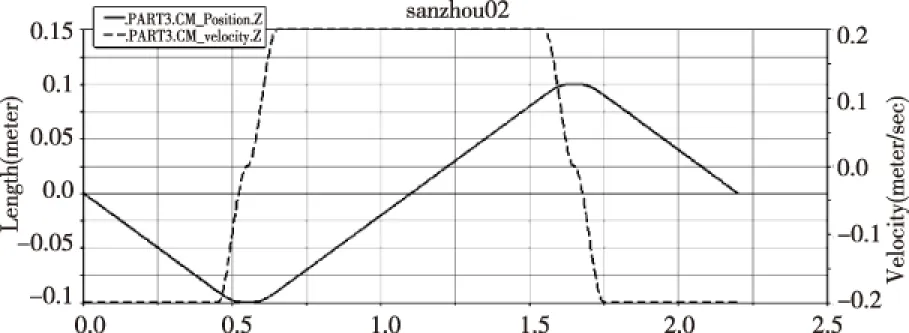
图3　X轴滑块运动速度与位移曲线图

由于Y轴滑台的尺寸与X轴一致，有效行程也相同，Y轴的运动情况和X轴相同，可直接将X轴编写好的程序函数导入到Y轴运动副中，得出Y轴的运动仿真情况，如图4所示。

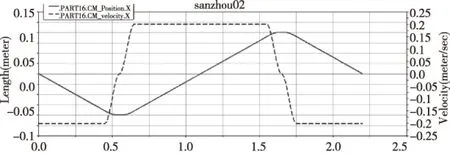
图4　Y轴滑块运动速度与位移曲线图

模拟Z轴运动滑块的工作运动状态。先向Z轴的底端以0.2 mm/s的速度运动0.2 s，在0.2 s至0.3 s内减速至零，此时运动滑块位于Z轴底端附近；在0.3 s至0.4 s内以垂直向上方向加速至0.2 mm/s ，匀速运动0.4 s后在0.1 s内减速为零，运动滑块位于Z轴顶端；再次反方向(滑块垂直往下端移动)加速0.1 s至速度为0.2 mm/s，后匀速运动0.2 s再减速停止在初始位置。Z轴滑块的位移与速度曲线图如图5所示。

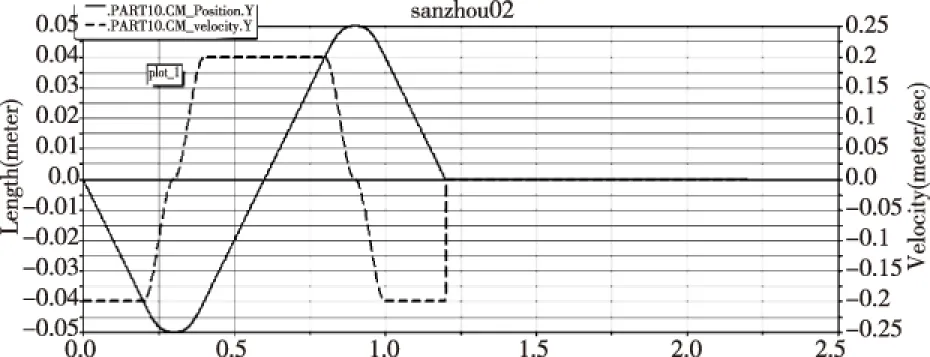
图5　Z轴滑块运动速度与位移曲线图

运用ADAMS模拟工作状态下执行机构的运动情况，查看三轴滑台的组合运动情况。通过计算分析和仿真，可以很明晰地查看出各伺服滑台在相互运动过程中，X轴滑块沿X轴运动轨迹范围为200 mm，Y轴滑块沿Y轴运动轨迹范围为200 mm，Z轴滑块沿Z轴运动轨迹范围为100 mm，三轴滑块在运动过程中均没有出现干涉或碰撞现象。

3　执行机构振动分析

3.1执行机构振动模型

影响精密机械加工精度最常见的因素就是机械的振动。在实际工作中，由于载荷的运动以及悬臂结构自身的移动，悬臂梁式执行机构会产生振动。因此对执行机构进行振动分析是十分必要的。

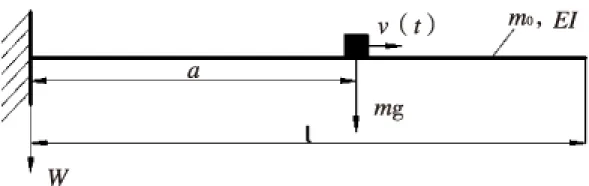
图6　悬臂梁-移动质量块模型

三轴悬臂梁式执行机构中，Y轴伺服滑台电机端固定在X轴连接板上，另一端悬臂，Z轴滑台装载在运动滑块上沿Y轴滑台作直线运动。将Y轴滑台简化成固定的悬臂梁模型，运动滑块视作移动质量块，此时的运动系统可当成是悬臂梁-移动质量块模型，如图6所示。

利用Euler-Bernoulli梁模型和达朗伯原理，建立移动质量块作用下，悬臂梁的运动方程、边界条件和初始条件为：

W(0，t)=W′(0，t)=W″(1，t)=W″′(1，t)=0

式中：W(x，t)为悬臂梁各点t时刻横向振动位移；m为移动质量(kg)；v为速度(m/s)；m0为单位长度梁的质量(kg) 。利用Duhamel积分和数值迭代算法来求解，可得到悬臂梁横向振动的相应位移。

建立执行机构仿真模型时，主要是将实体模型中的刚性结构件柔性化处理。根据执行机构中各滑台所受载荷和装配形式的不同，只针对受载后变形量较大、产生振动的Y轴滑台做柔性化处理。而X轴与水平固定台装配在一起，水平固定台可看成质量无限大的物体，系统工作时，X轴滑台不产生振动。

本文选择模态中性文件导入法，建立受载后变形量较大、产生振动的Y轴滑台的柔性体。将执行机构三维模型进行简化，建立Y轴刚性体。简化后的模型成为一个整体，外形结构尺寸与Y轴滑台一致。在SolidWorks中将Y轴滑台模型保存为可与ANSYS交换的Parasolid格式，将文件导入ANSYS中，利用ANSYS软件创建Y轴滑台模态中性文件(.mnf文件)[4-5]。将模型视作一个零件，利用SolidWorks的测量模块测量模型的体积，并分析计算得出模型的密度DENS=8 680 kg/m3，定义材料弹性模量E=2.07e11 Pa，泊松比λ=0.3。采用智能网格划分方法对Y轴滑台模型进行网格划分，划分网格如图7所示。

结合Y轴滑台与X轴连接板的实际接触情况，建立刚性接触区域，如图8所示。

图7　Y轴滑台网格模型　　　图8　创建刚性区域

完成刚性区域的创建之后，运用ANSYS软件提供的ADAMS.mac宏命令生成模态中性文件。输出.mnf文件之前，设置模型分析类型为model，抽取模态数为3阶模态。

3.2执行机构振动仿真

在ADAMS软件中导入刚性模型[6-8]，复制已导入的刚性模型并平移，如图9所示。

删除原模型Y轴伺服滑台的各个零部件，再导入.mnf文件，直接完成零件替换，生成刚柔耦合模型，如图10所示。

图9　复制并平移刚性模型

图10　刚柔耦合模型

分别建立执行机构的刚性模型和刚柔耦合模型，同时在ADAMS软件中进行动力学仿真分析[9-10]。执行机构的动力学仿真旨在模拟工作状态下，执行机构各滑台的运动情况，研究分析实际工况下系统的振动特性。为了清晰地分析执行机构的振动情况，编写各运动副的位移驱动函数，模拟执行机构系统实际工况下，运动滑块从电机端运动至底端整个过程中系统的振动情况。分析两种模型的振动情况，分别取两种模型中的Z轴运动滑块作为振动输出对象，选取Z轴运动滑块在Y-Z平面的位移时间曲线进行振动分析，如图11-图14所示。

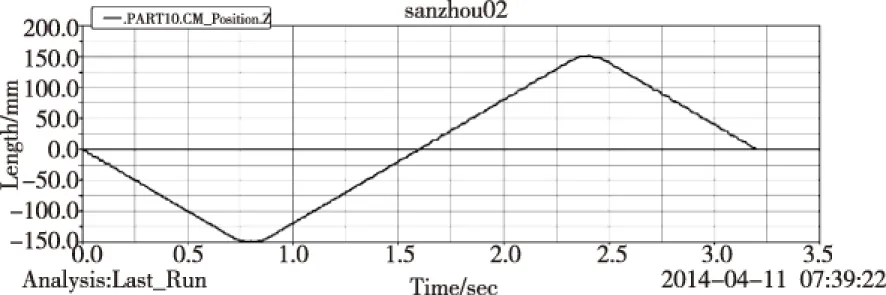
图11　刚柔耦合模型中Z轴滑块位移-时间图

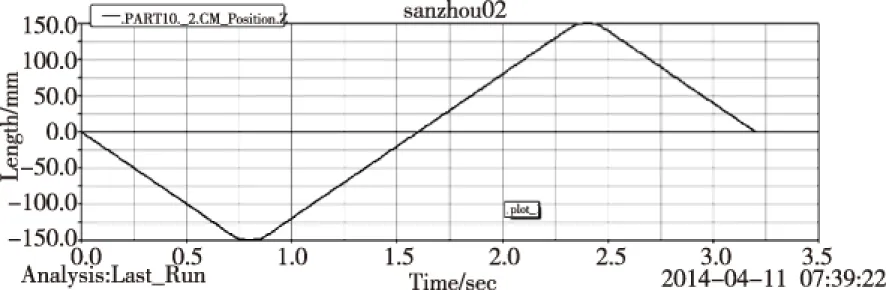
图12　刚性模型中Z轴滑块位移-时间图

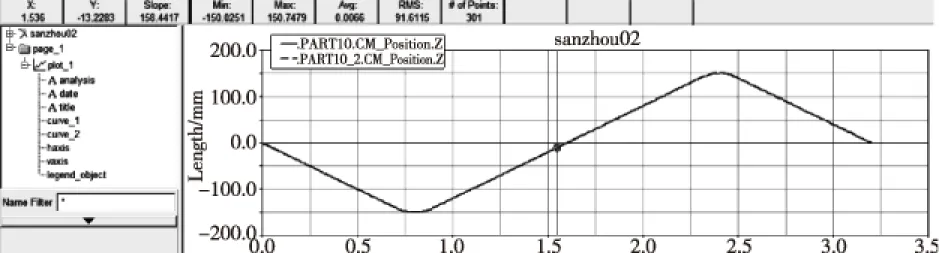
图13　两种模型的位移-时间曲线图对比

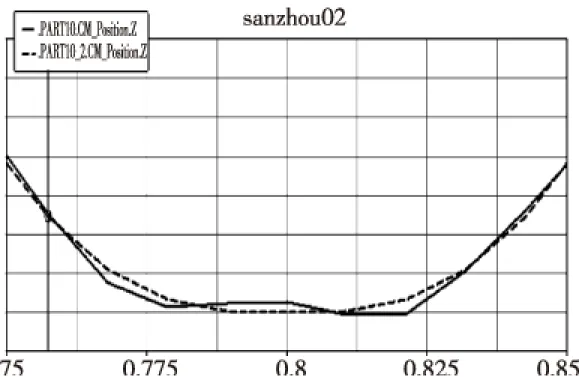
图14　两种模型的位移-时间曲线峰谷位置局部放大图

图14为两种模型的位移-时间曲线峰谷位置放大图，图中实线为刚柔耦合模型的位移-时间曲线，虚线为刚性模型的位移-时间曲线。由图可知，刚性模型中运动滑块的位移曲线图比刚柔耦合模型中滑块的位移曲线图平滑。刚柔耦合模型中滑块的位移曲线图有微小不规则的抖动，产生了微小的振动。两条曲线的走向一致，基本重合，两条直线之间的平均位移差为0.006 6 mm，未超出系统的精度要求0.02 mm。由刚柔耦合模型的位移-时间曲线可知，靠近梁的自由端时，梁的振动幅值明显增大，故执行机构系统的最大振动位移值出现在靠近悬臂梁自由端。为了减小运动滑块在Y轴底端位置的振动幅值，可以增大系统的弯曲刚度，改变U型基座的材料，改进结构等。

4　结束语

通过对3D打印系统的工作精度、工作目标以及打印喷头空间运动范围等进行综合分析，选用悬臂梁式执行机构。建立悬臂梁式执行机构的三维模型，运用虚拟样机技术在ADAMS中，对执行机构进行运动学仿真，模拟实际工作中执行机构各滑台的运动情况，确保机构设计正确。同时运用ANSYS和ADAMS建立执行机构的刚柔耦合动力学模型。在ADAMS中完成执行机构的动力学仿真。校验执行机构模拟实际工况下系统的最大振动位移值，使设计结果满足精度要求，同时找到系统最大振动位移值位置，可为结构优化提供依据。

[1]刘欣灵. 3D打印机及其工作原理[J].网络与信息,2012(02)：30.

[2]牛晰.三维打印机机型发展与趋势分析研究[J]. 机械工程师, 2015(06)：108-110.

[3]赖月梅.基于开源型3D打印机(RepRap)打印部件的机械性能研究[J].科技通报,2015,31(8):235-239.

[4]刘平安.详解ANSYS有限元分析[M].北京：电子工业出版社，2015.

[5]王新荣.ANSYS有限元基础教程[M].北京：电子工业出版社，2015.

[6]姜洪奎,宋现春,唐文成,等.基于虚拟样机技术的滚珠丝杠副的滚珠循环反向过程仿真和优化设计:2010国际数字科技博物馆学术论坛暨第二届数字科技馆技术与应用研讨会论文集[C].科学技术文献出版社, 2011.

[7]林坤,董桂鹏,王锡山,等.基于 ADAMS 的装配机械手振动仿真与分析[J].机械设计,2012,29(12):43-45.

[8]刘俊,林砺宗,刘小平,等. ADAMS 柔性体运动仿真分析研究及运用[J].现代制造工程, 2004(5)：53-55.

[9]马强，陈志,张小超，等. 基于ADAMS的果树采摘机械臂的运动仿真分析[J].农机化研究，2013(5)：37-40.

[10]廖伯瑜, 周新民, 尹志宏. 现代机械动力学及其工程应用: 建模, 分析, 仿真, 修改, 控制, 优化[M]. 机械工业出版社, 2004.

Simulation analysis of the 3D printer actuator

YU Xuan, ZHENG Yinhuan

The actuator is a key part of the 3D printer, and it can influence the accuracy and stability of the system. In this study, we established the 3D model of the actuator, carried out its kinematic simulation in ADAMS, established a rigid-flexible coupling dynamic model by ADAMS and ANSYS, and analyzed the vibration of the model. The results showed that, in normal working state, the actuator could meet the requirements of accuracy and stability. This study provided reference for further improvement of the actuator.

3D printer; actuator，rigid-flexible coupling dynamic model，kinematic simulation

TH132

A

1002-6886(2016)04-0048-05

中央高校基本科研业务费专项资金资助(项目批准号：2013-IV-062)。

余轩(1993-)，男，研究生，主要研究方向：机电系统动力学。

郑银环(1974-)，女，副教授，博士，主要研究方向：机电系统动力学。

2016-01-15