基于AMESim的双轴惯性激振器特性研究*

2016-08-16朱东敏

现代机械 2016年4期

关键词：激振器激振力双轴

刘　威，苏　明，朱东敏

(1.贵州师范大学机械与控制仿真重点实验室，贵州贵阳550014；2.贵州成智重工科技有限公司，贵州贵阳550081)

基于AMESim的双轴惯性激振器特性研究*

刘威1，苏明1，朱东敏2

(1.贵州师范大学机械与控制仿真重点实验室，贵州贵阳550014；2.贵州成智重工科技有限公司，贵州贵阳550081)

为保证双轴惯性激振器安装和制造精度，对偏心装置的安装相位差、偏心质量等因素进行研究，基于AMESim软件建立了双轴激振器模型并进行仿真。结果表明偏心装置的安装相位差决定了激振力的方向角，两轴偏心块质量决定了激振力形状，激振方向能够通过调整两轴偏心块的安装角度来确定，激振力形状能够通过调整两轴偏心质量进行调整，为激振器的设计和安装提供了参考。

双轴惯性激振器激振力相位角偏心质量AMESim

0　引言

惯性式激振器是一种利用偏心块回转产生激振力，并施加到其他结构上的装置。工作时将激振器固定于被激件上，通过电机驱动激振器振动达到稳定状态，被激件便获得所需的运行轨迹，从而达到振动机械的要求。双轴惯性式激振器可以采用运动学同步的方法[1]，也可以采用自同步的方法[2]。运动学同步是通过齿轮传动来平衡两轴的运动变化，这种方法在设计安装上有一定的局限性，其价值体现在成本低、结构稳定、承载力强等。自同步是由两台电机分别驱动两个惯性激振器，在一定条件下，两个惯性激振器实现同步运转。文献[2]分析了自同步双轴平行惯性式激振器的动力学特性及实现自同步的条件；文献[3、4]理论分析了双转子自同步行为与振动；文献[5、6]理论分析了运动学同步双轴平行惯性式激振器的输送转速与偏心块初始安装角度的关系以及最佳的安装角位置选择。

本文利用AMESim软件对运动学同步的双轴惯性激振器进行建模及仿真，得出了在实验开始时激振器的转速变化以及稳定后的变化规律，同时还有电机驱动激振器运动所产生激振力的变化与偏心块的安装相位、相位差等的关系，可以为激振器设计提供参考。

1　双轴惯性激振器结构及受力分析

1.1激振器结构

运动学同步的双轴惯性激振器一般由两根转轴和一对齿轮组成，电机和皮带轮的作用下输出转矩到主动齿轮，主动齿轮带动从动齿轮旋转，实现两根转轴等速反向回转产生激振合力。双轴激振器的结构如图1所示。

在振动筛中，双轴激振器通常如图2进行布置。

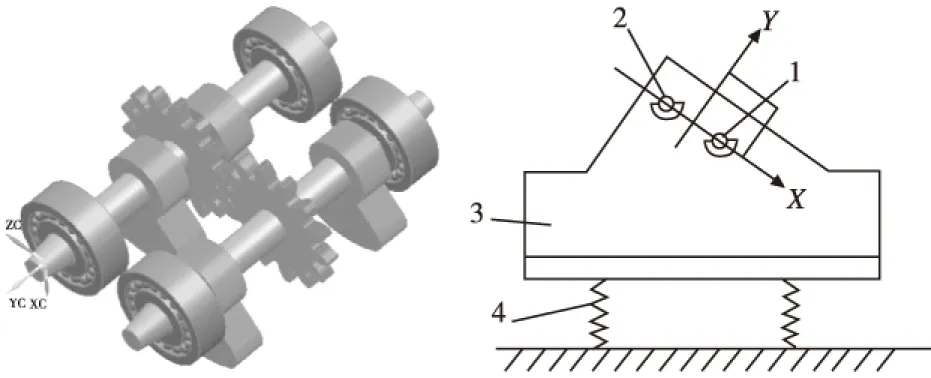
图1　激振器结构示意图　　图2　激振器布置示意图

1.2受力分析

建立坐标系，将激振器运动分解为x方向、y方向和绕坐标原点的旋转运动，其中x方向是两偏心块轴连线的方向，y方向与x方向垂直，过两偏心块质心。

激振器受力分析如图3所示，在1、3位置时，与轴垂直方向上的激振力处于叠加状态，在2、4位置时，与轴平行方向上的激振力处于抵消状态。

图3　双轴激振器受力分析图

图4　偏心块安装角度示意图

双轴激振器偏心块安装角度如图4。

双轴激振器每根轴的水平、竖直激振力可以表示为：

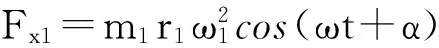
Fx1=m1r1ω21cos(ωt+α)

式中：Fx─x轴激振合力(N)；Fy─y轴激振合力(N)；Fx1─主动轴偏心块产生的x轴激振力(N)；Fy1─主动轴偏心块产生的y轴激振力(N)；Fx2─从动轴偏心块产生的x轴激振力(N)；Fy2─从动轴偏心块产生的y轴激振力(N)；m1、m2─主动轴、从动轴偏心总质量(kg)；r1、r2─主动轴、从动轴偏心距(m)；ω1、ω2—主动轴、从动轴偏心块角速度(rad/s)；α、α′—主动轴、从动轴偏心初始相位(rad)。

绕Z轴的扭摆力矩(φz方向)为：

2　激振器力矩方程

2.1激振电机机械特性

根据电力拖动理论，激振电机的机械特性实用表达式为[7]：

式中：Tm─激振电机最大转矩(N·m)；T─激振电机输出转矩(N·m)；s─激振电机转差率；sm─激振电机最大转差率。

通过查询电动机产品目录，可以得到上式参数。其中：

Tm=λMTN

式中：TN─激振电机额定转矩(N·m)；λM─激振电机过载倍数；TN─激振电机额定转矩(N·m)；PN─激振电机额定功率(kW)；nN─激振电机额定转速(rpm)；sN—额定转差率；kM—激振电机启动转矩倍数；n0—激振电机同步转速。

2.2激振器负载力矩

在激振器实际工作过程中，负载产生的惯性力不可忽略，同时偏心块的运转会导致系统产生偏心距，由此形成负载力矩，参考文献[8]，有：

T1=m1α1cosφ

T2=m2α2cosφ

式中：T1、T2─主动轴、从动轴负载力矩(N·m)；φ—两轴偏心块角位移(rad)；α1、α2─主动轴、从动轴角加速度(rad/s2)。

2.3轴承摩擦力矩

[2]，主动轴、从动轴摩擦力矩如下：

式中：Tf1、Tf2─主动轴、从动轴摩擦力矩(N·m)；Tv1、Tv2—主动轴、从动轴常值阻力矩(N·m)；f—摩擦系数；d1、d2─主动轴、从动轴轴承直径(m)。

2.4双轴激振器的转矩方程

[8]，建立主动轴转矩方程如下：

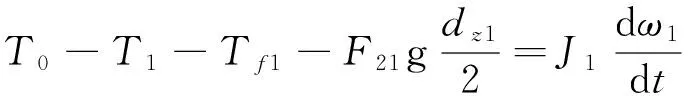
从动轴转矩方程如下：

式中：F12—主动轴施于从动轴齿轮的周向力(N)；J2—从动轴转动惯量(kg·m2)；dz2─从动轴齿轮分度圆直径(m)。

F21和F12是一对相互作用力，

给定：

r=r1=r2；

dz=dz1=dz2；

d=d1=d2；

ω=ω1=ω2；

f=f1=f2；

Tv=Tv1=Tv2。

综合以上各个部分的表达公式可以得到系统转矩方程：

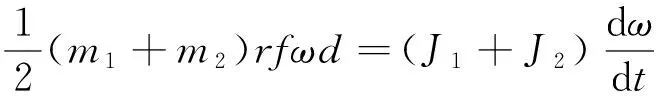
3　基于AMESim的双轴激振器建模与仿真

3.1双轴激振器建模

根据上述方程式，参考文献[9]，用AMESim软件中信号控制库元件构建双轴激振器仿真模型，如图5。

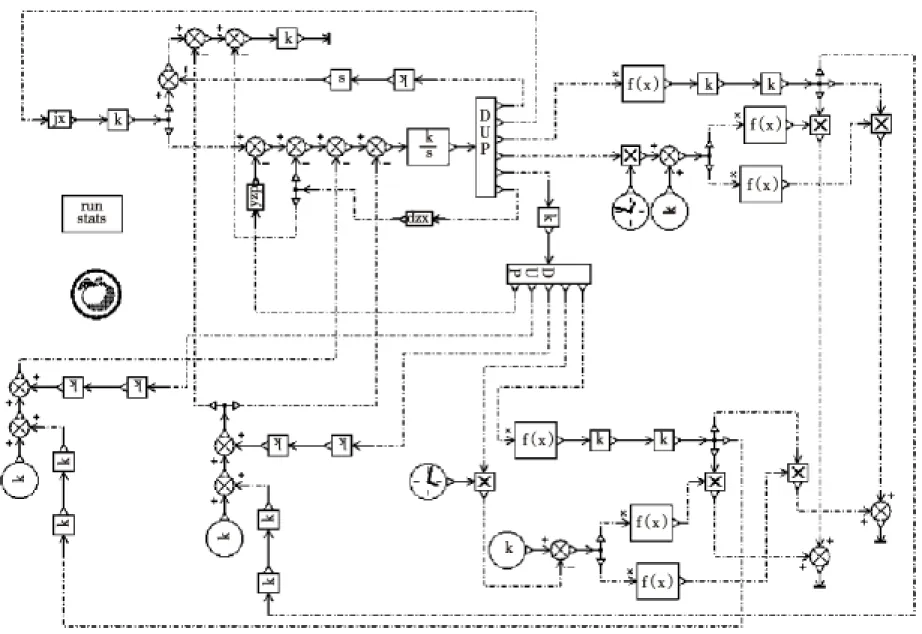
图5　双轴激振器AMESim模型

图5模型中显示小方框的区域是相关结构组成的超级元件，其详细的结构如图6所示，包括激振电机机械特性、两组偏心块的负载力矩。

图6　激振器模型中超级元件结构

3.2双轴激振器仿真

在模型中设置参数如表1。

表1　仿真参数设置

针对不同的相位角情况进行仿真，情况如表2。

表2　不同相位角仿真情况

得到：在不同安装相位角的条件下，所得轨迹仍然是直线形式，直线与x轴的正方向夹角随之变化，振幅大小也有一定波动；当安装相位差相同时，所得的结果是完全相同的。

改变m1，设定m1=16 kg，在不同相位角情况下再次进行仿真，情况如表3。

表3　改变偏心块质量时不同相位角仿真情况

得到：当双轴激振器的两轴偏心块质量不均衡时，得到的激振力形状为椭圆；当安装相位差相同时，所得的结果也是完全相同的。

比较表2、3，可以看出：当质量不均衡时表3所得椭圆长轴方向与质量均衡时表2所得直线方向是一致的，同时椭圆的长轴与直线的长度也是相等的。

4　总结与讨论

本文利用AMESim在机械、信号控制方面的优势，建立了物理仿真模型，通过相关参数的改变，进行动态分析，通过研究，可以得出以下结论：

1)在双轴惯性激振器中，偏心装置的安装相位差决定了激振力的方向角，同时也影响了激振力大小的波动范围，当相位差数值大小相等时，所得振幅相同。

2)在双轴惯性激振器中，两轴偏心块质量的均衡与否决定了激振力的形状，当偏心块质量相等时，激振力形状为直线，广泛应用于各种直线筛中；当偏心块质量不相等时，激振力形状为椭圆，可应用于各种椭圆筛中。

3)在AMESim中建立的双轴惯性激振器，参数可以随时调整，对于双轴惯性激振器设计有参考价值。

在工程实际中，还有许多其它参数对激振器产生影响，本文仅仅局限在三自由度情况下，对相位角及偏心质量进行了研究。

[1]褚亦清，梅凤翔．单质量双轴平行惯性式铅垂振动输送机的自同步效应[J]．矿山机械，1980(03)：18-23．

[2]闻邦椿．机械系统的振动同步与控制同步[M]．北京:科学出版社，2003.

[3]张楠，侯晓林，闻邦椿. 双转子自同步系统同步行为分析[J]．农业机械学报，2009，40(04):184-188．

[4]韩清凯，秦朝烨，杨晓光，等．双转子自同步系统的振动分析[J]．振动工程学报，2007，20(05):534-537．

[5]北京工业学院理论力学实验室．惯性式铅垂振动输送机激振器的偏心配置[J]. 起重运输机械，1976(04)：7-12．

[6]杨宗基，王国山，褚亦清，等．双轴平行惯性式铅垂振动输送机偏心块的最佳安装角[J]. 起重运输机械，1978(05)：6-9．

[7]吴浩烈．电机及电力拖动基础[M]．重庆:重庆大学出版社，2002:46-48.

[8]李桂枝．单激振电机拖动系统特性研究[J]．矿山机械，1996(08)：38-40．

[9]付永领，齐海涛.LMS Imagine. Lab AMESim系统建模与仿真[M]．北京:北京航空航天大学出版社，2011.

Research on the characteristics of the biaxial inertial vibration exciter based on AMESim

LIU Wei, SU Ming, ZHU Dongmin

To ensure the installation and manufacture accuracy of the biaxial inertial vibration exciter, we studied the phase difference and eccentric mass of the eccentric device. We built the model of the vibration exciter and carried out simulation based on AMESim. The results showed that, the direction angle of the excitation force was determined by the installation phase difference of the eccentric device, the shape of the excitation force was determined by the mass of the biaxial eccentric block, the excitation direction could be adjusted by adjusting the installation angle of the biaxial eccentric block, and the shape of the excitation force could be adjusted by adjusting the mass of the biaxial eccentric block. This study has provided reference for the design and installation of vibration exciters.

biaxial inertial vibration exciter，excitation force，phase angle，eccentric mass，AMESim