基于HELS方法的噪声诊断技术研究

刘丛志　王铃燕　任冰禹　马卢平　刘伟群　胡广地

西南交通大学,成都，610031



基于HELS方法的噪声诊断技术研究

刘丛志王铃燕任冰禹马卢平刘伟群胡广地

西南交通大学,成都，610031

基于赫姆霍兹方程最小二乘法(HELS)的噪声诊断技术，将赫姆霍兹方程应用于噪声诊断技术中，把声场中声压转化为一组线性无关的独立函数的叠加，使用最小二乘法根据已知的较少噪声信号准确高效地重建声源表面的声压。建立基于非线性优化理论的新型HELS-PSO模型进行噪声源识别和声场重建研究，在实验室中以音箱作为模拟噪声源，通过实验进行验证。实验结果验证了该算法的有效性和高效性，表明新算法的求解精度较高。

快速噪声诊断；赫姆霍兹方程；非线性优化模型；HELS-PSO算法

0　引言

汽车在运行过程中是一个复杂的噪声源系统，通过各种振动结构表面辐射出噪声。正确判断噪声源的具体发声零部件，可为采取有效的降噪措施提供依据。随着我国汽车用户对噪声、振动和舒适性等方面性能要求的提高，准确识别出汽车的噪声源、获取噪声的相关参数以提高汽车舒适性，就成了重要问题[1]。

在20世纪80年代中后期，一些学者开始通过近场全息和快速傅里叶变换组合的一种近场全息方法，重构平面源表面声场、柱表面源声场、封闭声源的几何表面声场以及任意规则外形的声源。随后，开始使用有限元法来求解声辐射逆问题，由于需要对整个边界进行离散，计算量较大，因此这种方法仅运用于低频较小空腔声源或可以测得微粒振速的声源[2]。进入20世纪90年代，边界元法开始运用在研究表面形状不规则的声源的声辐射问题中，相继出现了使用最小二乘法来近似重构源表面声场、运用边界元法来求解声辐射逆问题等方法[3]。近场全息理论和边界元法都需要较多的测量点，很多情况下受限于实践要求而无法完成声场重建，为了提高工作效率，赫姆霍兹方程最小二乘法(HELS)开始运用于声场重建，其需要的测量点数目远小于前几种方法要求的数目[4]。

Wang等[5]提出使用HELS法把声场中声压转化为独立的球谐函数的叠加，再使用最小二乘法根据已知的噪声信号来重建声源表面的声压。Wu等[6]联立HELS法和边界元法根据声场中较少的测量点，重构出了任意形状声源的声场。由于HELS方法计算效率极高，因此在工程实际中得到较为广泛的应用。

1　赫姆霍兹方程

假设声波介质是理想的均匀连续流体，且流体是完全弹性的，介质运动过程中没有能量损耗。声波要满足三个基本物理定律：牛顿第二定律、质量守恒定律、热力学定律。

(1)牛顿第二定律。包含在单元体积中动量的时间变化率加上经过体积x方向的净动量率必须等于作用在该体积x方向的力之和：

(1)

其中，p表示在位置x处t时刻的声压，ρ为介质密度，ux为介质流速。

(2)质量守恒定律。介质中因声波扰动，单位时间内流入体积元的质量与流出该体积元的质量之差应等于该体积内质量的增加或减少：

(2)

(3)热力学定律。在声波作用时，引起介质团压缩和伸张过程很快，近似地认为介质团与周围介质不发生热交换，即介质团状态的变化可视等熵绝热过程。表达式为

p=c2ρ

(3)

其中，c为声速。

联立式(1)～式(3)并忽略二阶以上的微量可得线性声学波动方程为[7]

(4)

对于单频简谐波，声场内任意位置(包括声源表面)上的声压可表示为

(5)

将其代入声学波动方程并应用傅里叶变换可得赫姆霍兹微分方程：

2p+k2p=0

k=ω/e

(6)

其中，p为声场中某点的声压；R为波数，ω为角频率；2表示拉普拉斯算子，在笛卡儿坐标系下为

采用分离变量法可解得赫姆霍兹方程在各坐标系下的解，即可对声场进行描述及研究声场分布特性[8-10]。

在直角坐标系(x,y,z)下，式(3)的解为

其中，A、B为常数，由边界条件确定。

在柱坐标系(r,θ,z)下，式(3)的形式为

利用分离变量法解得

p(r,θ,z)=Jm(krr)ej(mθ+kzz)

其中，Jm和Ym都是m次柱贝塞尔方程的特解，且是线性无关的；第一阶柱汉克尔函数Hm(1)(x)和第二阶柱汉克尔函数Hm(2)(x)都是柱诺依曼函数和柱贝塞尔函数的线性组合，分别表示一自中心轴向外发散的前进波和一向中心轴汇聚的反射波。

在球坐标系下，式(3)的形式为

其解为

2　HELS计算模型

2.1HELS方法原理

基于HELS方法的噪声诊断技术[11]，就是将赫姆霍兹方程应用于噪声诊断技术中，把声场中声压转化为一系列线性无关的独立函数的叠加，然后使用最小二乘法，根据已知的噪声信号来重建声场。该技术的实质是寻找一个在整个声场都通用的、较为简单的声压函数，并要求此声压函数只与位置有关。基于HELS方法的噪声诊断技术仅需要测量声场中较少点的声压，就可以较为准确、高效地重构出声场中其他点的声学信息，特别是声源表面的声振情况[12]。声场中(包括声源表面)任意一点x处的声压为[13-14]

(7)

其中，Ci为系数权重，ψi为赫姆霍兹方程式(3)相互独立且线性无关的特解。测量点的数量M和独立函数的项数N的大小直接影响着HELS模型的计算效率和精度，文献[15]中给出了一种确定测量点数目M和独立函数项数N的方法，即

N=ka,max+1

M≥1.4N

其中，ka,max为声源辐射声波的最大量纲一频率。

先通过实验测得已知声场中某些点的声压，然后求解系数权重Ci，从而利用式(7)达到重构声场的目的。设实验测得声场中m个测量点的声压为

p(xi)=pii=1,2,…,m

其中，xi表示声场中第i个测量点的位置。若选择一组n(n≤m)个独立函数，则

(8)

其中，ψmn为第n个独立函数在第m个测量点的值。式(8)的解为

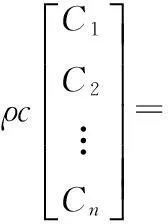
(9)

当所取独立函数ψi(x)线性无关时，Ci的值可以由式(9)唯一确定。进而重建声场，得到声场中任意点(包括声源表面)的声压为

(10)

声源表面某点xs处的表面振速为

(11)

因此，利用HELS方法即可根据声场中部分测量点的声压信息来确定声源表面的声压。

2.2常用独立函数选取

为使独立函数更为合理地模拟声场中的声压分布，要尽量根据声源的形状、理论声压模型选取合适的独立函数，同时还应该尽可能选取简单的线性无关的独立函数，以减少计算量。

(1)球谐函数。脉动球的声场声压的理论计算公式为

其中，r表示计算场点距脉动球球心的距离，a表示脉动球的半径。

由于球汉克尔函数中的球诺依曼函数在r=0处没有意义，故选取球贝塞尔函数作为最终选取的独立函数：

波数k=0.5，选择6个球谐函数作为一组线性无关的独立函数，则HELS计算模型为

(12)

其中，线性独立函数为

球贝塞尔函数为

勒让德函数为

(2)柱波函数。圆柱声源产生的声场声压的理论计算公式为

式中，εm为诺依曼系数。

则所选取的独立函数为

式中，m为非负整数。

波数k=0.5，选择6个球谐函数作为一组线性无关的独立函数，则HELS计算模型为

(13)

(3)点源函数。选取声源内部某点Q作为源点，根据赫姆霍兹微分方程的解和独立函数的选取原则，选取的独立函数为

其中，r为声场中的任一点与源点Q之间的距离。

波数k=0.5，选择6个球谐函数作为一组线性无关的独立函数，则HELS计算模型为

(14)

其中，线性独立函数为

3　非线性二次优化模型

根据已知的部分声场信息求解出系数矩阵C，即可达到重构声场的目的。由解矩阵方程建立的逆问题求解模型，算法实现复杂，并且对测量误差非常敏感，常常因为病态矩阵和测量误差而导致结果的不稳健性，无法保证声场重建的精度[16]。因此，建立非线性二次优化模型更为精确地搜索系数矩阵的全局最优解，在一定程度上抑制模型的不稳健性。

(15)

采用非线性优化模型求解误差平方和的最小值，即可识别噪声源。粒子群优化算法(PSO)是一种基于群体智能的启发式全局随机搜索算法，对非线性问题具有较强的全局搜索能力[17]。本文采用PSO利用MATLAB软件求解非线性优化模型，可以实现噪声源的全局搜索。

4　实验验证分析

4.1传感器阵列设计

传感器阵列是由许多传感器组成的具有一定几何结构排列的阵列，其基本原理是波束形成技术，该技术将多元基阵中各阵元的输出信号经过一定的处理，形成具有某些可视化的空间特征[18]。

本文采用两种传感器阵列对声场进行测试，采用图1所示的单支架布置方案，利用6个传声器对所选取的54个测量点进行扫描采样。如图1a所示的圆形阵列方案中，由装有6个传声器的单支架从1#位置依次旋转到9#位置，完成54个测量点的测试工作；图1b所示的矩形阵列中单支架从1#位置依次平移到9#位置，完成声压测试工作。

(a)圆形阵列　　　　　　(b)矩形阵列图1　传声器阵列设计布置方案图

4.2声场声压测试实验

如图2所示，测试过程在5.0 m×4.3 m×4.0 m的半消声室内进行，用扬声器作为模拟声源。对单个噪声源、双噪声源依次进行圆形阵列和矩形阵列测试，分别对声场中所选择的54个测量点测得其声压值。其中左图为矩形阵列测试实验，右图为圆形阵列测试，左图中1为传声器，2为传声器阵列支架，3为模拟噪声源。

图2　声压测试实验

4.3求解结果分析

4.3.1噪声源识别

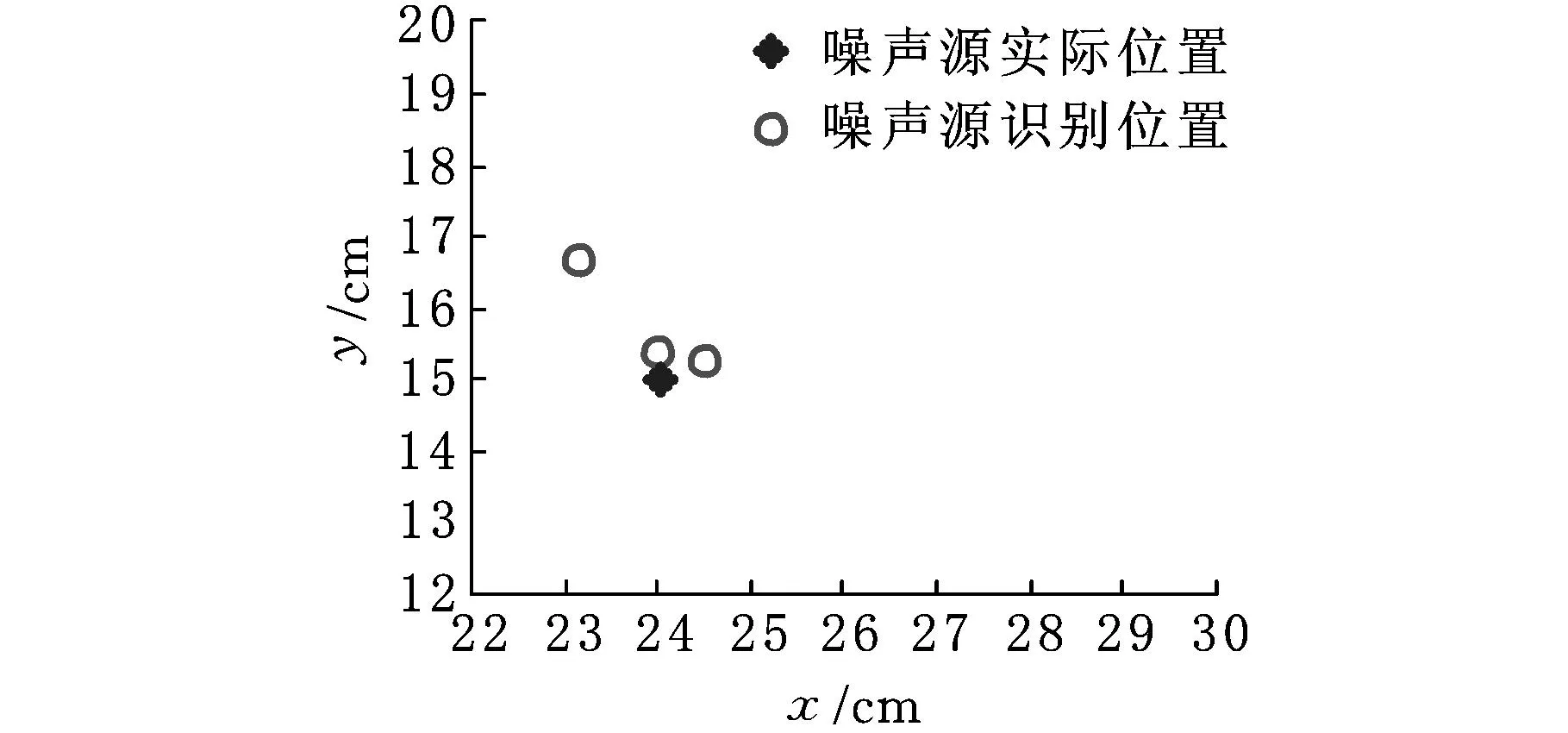
图3　单噪声源识别结果

图4　双噪声源识别结果

如图3、图4所示，选择不同的独立函数时的噪声源识别位置(图中圆圈位置)与实际测量位置(图中黑方形位置)。由图可见，HELS-PSO模型可以很好地对噪声源进行识别，且对单噪声源位置的识别结果比多噪声源的识别位置更接近于其真实位置。

4.3.2声场重建

为了衡量声场重建的整体效果优劣，定义声场重建平均残差为

(16)

表1　声场重建误差分析

由重建误差分析结果可见：选择球谐函数作为独立函数的重建误差较大，对单个噪声源的声场重建结果的精度比多噪声源的精度高，圆形阵列测试结果的声场重建精度较矩形阵列的精度高。同时也说明，独立函数、传声器阵列的布置方案对声场重建精度的高低有直接的影响。

4.3.3两种算法的求解误差对比

以测得的实际声场声压值作为参考，两种算法的声场重建误差如表2所示。可见，HELS-PSO算法比传统HELS算法的求解误差更低，但是选取柱波函数时两者的效果相差不大。

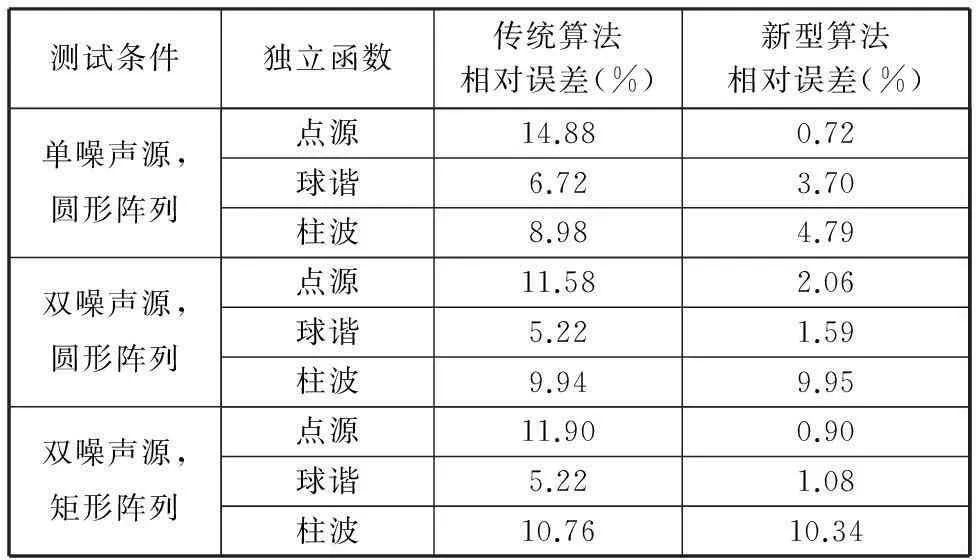
表2　两种不同算法的求解误差对比

5　基于MTALAB-GUI的系统软件设计

为了实现人机交互，本文利用MTALAB-GUI图形用户界面功能完成了系统软件设计，实现了数据分析处理、参数设置、算法自定义和结果显示等功能。

如图5所示，菜单栏设计了5项主菜单和22个子菜单。用户可利用该软件选择不同的独立函数，实现声场重建三维和二维等高线图的交互显示，并显示噪声源识别和误差分析结果。

图5　设计的用户界面

6　结束语

本文以HELS为主要研究对象，建立了HELS-PSO模型求解声学逆问题。通过实验测得声场分布，选择不同的独立函数分别进行了噪声源识别和声场重建，利用实验验证了该方法的有效性，并得出了一些有指导意义的结论。为了实现人机交互与噪声的快速识别，还设计了声场快速重建系统软件。

[1]吴志明.车辆噪声与振动测试系统研究[D].秦皇岛：燕山大学，2011.

[2]Petyt M，Lea J，Koopmann G H. A Finite Element Method for Determining the Acoustic Modes of Irregular Shaped Cavities[J]. Journal of Sound and Vibration，1976，45(4)：495-502.

[3]杨瑞梁.快速噪声诊断技术——HELS方法的理论及工程应用研究[M].郑州：黄河水利出版社，2006.

[4]张海滨，蒋伟康，薛玮飞,等.基于HELS法的多源相干声场重建研究[J].振动与冲击，2008,27(1)：93-96.

Zhang Haibin, Jiang Weikang, Xue Weifei, et al. Acoustic Field Reconstruction of Coherent Multi-sound Source Based on HELS Method[J]. Journal of Vibration and Shock, 2008, 27(1):93-96.

[5]Wang Z，Wu S F. Helmholtz Equation-least-squares Method for Reconstructing the Acoustic Pressure field[J]. The Journal of the Acoustical Society of America，1997，102(4)：2020-2032.

[6]Wu S F，Yu J. Reconstructing Interior Acoustic Pressure Fields Via Helmholtz Equation Least-squares Method[J]. The Journal of the Acoustical Society of America，1998，104(4)：2054-2060.

[7]庞剑，諶刚，何华.汽车噪声与振动——理论与应用[M].北京：北京理工大学出版社，2006.

[8]吴九汇.噪声分析与控制[M].西安：西安交通大学出版社，2011.

[9]Baiges J，Codina R. A Variational Multiscale Method with Subscales on the Element Boundaries for the Helmholtz Equation[J]. International Journal for Numerical Methods in Engineering，2013，93(6)：664-684.

[10]Chardon G，Cohen A，Daudet L. Reconstruction of Solutions to the Helmholtz Equation from Punctual Measurements[C]//9th International Conference on Sampling Theory and Applications.Bremen,Germany,2013:2013.

[11]Wu S F. The Helmholtz Equation Least-Squares Method [M]. New York：Springer，2015.

[12]Natarajan L K，Wu S. Reconstruction of Normal Surface Velocities on a Baffled Plate Using Helmholtz Equation Least Squares Method[J]. The Journal of the Acoustical Society of America，2011，129(4)：2448-2448.

[13]张金圈.基于波束形成技术的噪声源识别与声场可视化研究[D].合肥：合肥工业大学，2010.

[14]Sean F W，Zhao X. Combined Helmholtz Equation-least Squares Method for Reconstructing Acoustic Radiation from Arbitrarily Shaped Objects[J]. Journal of the Acoustical Society of America，2002，112 (1)：179-188.

[15]Wu S F，Rayess N，Zhao X. Visualization of Acoustic Radiation from a Vibrating Bowling Ball[J]. Journal of the Acoustical Society of America,2001,109(6) :277l-2779 .

[16]薛玮飞.机械噪声源辨识与特征提取的研究[D].上海：上海交通大学，2007.

[17]Garnier S，Gautrais J，Theraulaz G. The Biological Principles of Swarm Intelligence[J]. Swarm Intelligence，2007，1(1)：3-31.

[18]齐娜，孟子厚.声频声学测量技术原理[M].北京：国防工业出版社，2008.

(编辑郭伟)

Research on Noise Diagnosis Technology Based on HELS Method

Liu CongzhiWang LingyanRen BingyuMa LupingLiu WeiqunHu Guangdi

Southwest Jiaotong University,Chengdu,610031

The noise diagnosis technology based on HELS applied the Helmholtz equation for noise diagnosis. It transformed the superposition of sound pressure into superposition of a set of linear independent functions. Then the method of least squares was used to reestablish the surface pressure of the sound source according to the known noise signals. The paper innovatively established a new type of HELS-PSO model to research the noise source identification and sound field reconstruction in order to improve solution accuracy. In the experiments the speakers were as simulated noise source and verified by experiments. The experimental results verify the effectiveness and efficiency of the algorithm and the accuracy of the new algorithm is higher than that of the traditional HELS algorithm.

fast noise diagnosis; Helmholtz equation; nonlinear optimization model; Helmholtz equation least squares(HELS)-particle swarm optimization(PSO) algorithm

2015-11-11

中央高校基本科研业务费专项资金资助项目(SWJTU12CX036)；四川省应用基础研究(重大前沿)项目(2015JY0281)；四川省重大科技成果转化专项(2015CC0003)；四川省国际科技合作与交流研究计划项目(2015HH0062)；西南交通大学研究生创新实验实践项目(YC201402104)

TB533DOI：10.3969/j.issn.1004-132X.2016.07.006

刘丛志，男，1989年生。西南交通大学机械工程学院硕士研究生。研究方向为汽车及发动机检制。王铃燕，女，1988年生。西南交通大学机械工程学院硕士研究生。任冰禹，男，1990年生。西南交通大学机械工程学院硕士研究生。马卢平，男，1990年生。西南交通大学机械工程学院硕士研究生。刘伟群(通信作者)，男，1983年生。西南交通大学机械工程学院讲师。胡广地，男，1964年生。西南交通大学机械工程学院教授、博士研究生导师。