一种基于位姿反馈的工业机器人定位补偿方法

何庆稀　游震洲　孔向东

1.温州职业技术学院，温州，325000　2.温州大学瓯江学院，温州，325000



一种基于位姿反馈的工业机器人定位补偿方法

何庆稀1游震洲1孔向东2

1.温州职业技术学院，温州，3250002.温州大学瓯江学院，温州，325000

为了提高工业机器人的绝对定位精度，提出了一种基于末端位姿闭环反馈的机器人精度补偿方法。该方法通过激光跟踪仪测量实时跟踪机器人末端靶标点的位置来监测机器人末端的位姿，并通过对靶标点的实际位置和理论位置进行匹配获得机器人末端的位姿偏差。工业机器人系统与激光跟踪测量系统通过局域网进行数据通信，并根据位姿偏差数据对机器人末端的位姿进行修正。最后通过实验对基于末端位姿闭环反馈的机器人精度补偿方法进行验证，实验表明,经过位姿闭环反馈补偿后机器人末端位置误差最大幅度可以降低到0.05 mm，姿态误差最大幅度可以降低到0.012°。

工业机器人；绝对定位精度；位姿闭环反馈；激光跟踪仪

0　引言

工业机器人具有高度柔性、通用性和易操作的特性，广泛应用于汽车、船舶、航空等工业生产领域，特别是因其具有较高的重复定位精度而广泛应用于焊接、喷涂、搬运等工作中。相对于其较高的重复定位精度，机器人绝对定位精度较低[1]。在工业应用中，影响机器人绝对定位精度的因素很多，主要可以分为两大因素[2]：一是机器人运动学模型误差，包括连杆长度误差、连杆距离误差；二是机器人动力学模型误差，主要包括机器人关节传递误差、齿轮传动误差、运动摩擦等。目前提高机器人绝对定位精度的方法主要有两种，一种是对机器人的运动学模型参数进行重新标定。基于运动学模型的参数标定主要包括运动学模型建模、测量、参数识别和误差补偿四个部分[3]。Veitschegger等[4-5]在D-H模型[6]的基础上提出了MD-H模型，揭示了机器人连杆参数的微小变化和机器人末端位姿变化之间的线性关系。国内基于模型的参数标定方法普遍是在建立D-H运动学模型的基础上,识别出机器人的几何参数并进行误差补偿[7-9]。机器人标定技术不仅需要深入研究复杂的机器人正逆运动学模型和参数识别算法，而且存在两方面的显著局限，一是补偿后定位误差为0.2 mm，精度几乎没有提升空间，二是并非对测量空间内所有点均能实现有效补偿。另一种提高机器人定位精度的方法是，在工业机器人末端执行器上添加反馈系统，如光学测量系统[10]、视觉测量系统[11]和力检测系统[12]等。Wang等[13]使用激光跟踪仪实时补偿工业机器人末端三轴动力头的运动误差，但为了降低系统复杂性与成本，该方法只使用在三自由度的机器人上。Vincze等[14]提出了一种采用激光跟踪仪与视觉系统实时测量机器人位姿的方法，其中机器人的位置信息由激光跟踪仪获取，机器人的姿态由激光跟踪仪与视觉系统共同获取。

为了提高机器人的定位精度，本文提出一种基于工业机器人末端位置和姿态闭环反馈的定位补偿方法。

1　基于位姿反馈的精度补偿原理

1.1系统组成与集成

基于末端位姿反馈的机器人精度补偿系统主要包括工业机器人和激光跟踪测量系统两个部分。工业机器人作为执行主体，主要是实现对末端执行器或工件的夹持和定位。末端执行器或工件通过法兰盘固定安装在工业机器人的末端法兰上，与工业机器人构成一个整体。机器人通过调整末端的位姿来实现末端执行器或工件的定位。激光跟踪测量系统用于实时地测量机器人末端执行器或工件的位置和姿态。根据刚体的特性，只需要在末端执行器或工件上布置三个以上不在一条直线上的靶标点，就可以实现对位置和姿态的测量。对此，开发了专用的测量软件，可以通过比较靶标点的设计理论值和激光跟踪仪的实际测量值，计算末端执行器或工件的位姿偏差。实际上，激光跟踪仪与工业机器人之间构成了一个基于末端位姿的闭环反馈系统，激光跟踪仪作为机器人的外置传感器，实时监测并返回机器人末端的位姿误差(图 1)。

图1　位姿反馈原理图

图2　系统集成

工业机器人和激光跟踪仪测量系统通过OPC服务器进行数据通信，如图2所示。这些数据包括位姿偏差数据、机器人坐标系数据等。具体而言，测量软件驱动激光跟踪仪完成对靶标点的自动化测量任务，并通过读取OPC服务器中的机器人法兰坐标系数据来计算机器人的位姿偏差，并将偏差数据写入OPC服务器。机器人在完成定位后需要往OPC服务器中写入当前机器人法兰坐标系，并读取来自测量软件的位姿偏差数据。

1.2位姿补偿方法

由于影响机器人本身的定位精度的因素很多，包括运动学模型误差、齿轮传动误差、关节运动摩擦等动力学模型误差和温度、载荷等，机器人在位姿补偿过程中也会带入误差。因此，基于位姿反馈的工业机器人定位精度补偿方法的实现是一个逐渐逼近理论位姿的过程，具体操作流程如下：

(1)根据CAD模型，确定机器人末端的理论工作位置和姿态，规划机器人运动路径，并编制相应的机器人控制程序。根据机器人末端的理论位姿，获得机器人末端执行器或工件上靶标点的理论坐标。

(2)运行机器人控制程序，实现机器人在自身精度条件下的初定位。

(3)机器人完成定位后，激光跟踪仪测量靶标点的实际坐标。通过与其理论坐标进行匹配，计算当前机器人末端执行器或工件的位姿偏差。

(4)进行姿态偏差评判，若位姿偏差满足工艺要求，流程跳转执行(6)；若位姿偏差超出工艺要求，则需要对机器人的位姿进行修正，继续执行(4)。

(5)通过工业局域网络，激光跟踪仪将位姿偏差数据传输给工业机器人控制系统。工业机器人根据位姿偏差数据对机器人末端的位姿进行调整。机器人调整完成后，流程返回(3)。

(6)机器人定位结束。

2　机器人末端位姿误差评价

2.1机器人位姿误差描述

机器人位姿误差包括机器人末端在机器人坐标系下的位置偏差和姿态偏差。末端执行器或工件通过法兰固定安装在机器人末端后，与机器人法兰构成一个整体。因此，机器人末端执行器或工件的位姿误差问题可以转换为机器人末端法兰的位姿误差问题。机器人位姿反馈补偿流程如图3所示。

图3　位姿反馈补偿流程

2.1.1机器人末端位置误差

机器人末端的位置误差表示机器人末端的实际位置和理论位置之间的差值，即

ΔT=T-T0

(1)

式中，T和T0分别为机器人末端的实际位置和理论位置。

2.1.2机器人末端姿态误差

机器人末端姿态误差用四元数表示：

(2)

式中,[axayax]是对应的欧拉旋转轴;θ是欧拉旋转角。

该四元数表示机器人末端的当前姿态和理论姿态的差值，即在当前机器人末端姿态下，机器人末端通过围绕[axayaz]T旋转θ角度后即可得到理论姿态。

姿态四元数和传统的方向余弦矩阵之间可以通过下面的公式进行转换:

(3)

2.2位姿误差评价算法

一个刚体的位置和姿态可以通过不共线的三个点的位置来确定。工件通过法兰安装在机器人末端后，可将工件与机器人末端看作是一个刚体。在工件上布置三个以上的靶标点，通过这些靶标点的位置就可以确定当前机器人末端的实际位姿。进一步通过比较靶标点的理论值和实际值，运用刚性匹配算法可以得到机器人末端的位姿偏差。

假设靶标点在机器人坐标系W下的理论位置为WPai，实际测量值为WPbi。首先，需要将靶标点的理论值和测量值都转换到工业机器人的工具坐标系(与机器人末端法兰坐标系F重合)下：

(4)

(5)

根据刚性匹配原理，靶标点的理论坐标和实际坐标之间满足如下关系：

Pbi=ΔRPai+ΔT+ξi

(6)

式中，ΔR和ΔT分别为姿态偏差和位置偏差;ξi为第i个靶标点的测量误差。

为了求解位姿偏差，构建如下最小二乘模型:

(7)

式中，N为靶标点的数量。

(8)

显然，式(8)的最小化问题等同于求取下式的最大值[16]：

(9)

式中，Δq是姿态误差ΔR对应的四元数。

式(9)可以改写成以下矩阵形式：

Σ=qTMq

(10)

此时，姿态误差四元数Δq取矩阵M的最大特征值对应的特征向量。

最后，位置误差矩阵可以通过下式计算得到：

(11)

3　实验

本文通过实验对基于位姿闭环反馈的机器人定位精度和重复定位精度进行了验证。实验中，工业机器人采用库卡公司的重载机器人KR360L280-2 (最大载荷2800 N)，标称重复定位精度为0.08 mm。测量设备采用徕卡公司的激光跟踪仪AT-901LR。该仪器在全量程范围内(水平方向360°，垂直方向正负45°，最大测量距离80 m)对单点的测量不确定度为基础值15 μm与增量值(每米增量值为6 μm)之和。在机器人末端安装三个靶标点作为位姿检测点。

为了对机器人在经过位姿闭环反馈补偿前后的末端位姿精度和重复定位精度进行比较，在整个机器人的作业空间内随机选择了若干位姿作为理论参考位姿。整个实验过程可以按如下步骤进行：首先，通过机器人运动程序驱动机器人自行运动到目标位姿。在机器人定位完成后，通过激光跟踪仪测量末端靶标点的坐标，来计算当前的位姿偏差。接着，运用本文提出的基于位姿闭环反馈的位姿精度补偿方法对机器人的末端进行补偿，然后记录补偿以后的机器人位姿误差。最后对补偿前后机器人的定位精度进行比较。以其中某个参考位姿的补偿过程为例进行说明，图4记录了整个位姿补偿过程中机器人末端位姿偏差的缩减情况。从图4可以看出，在经过仅仅三次位姿误差补偿后，机器人的末端位姿便得到了明显的提高，其中位置误差从1.4 mm减少到0.081 mm，角度误差从0.712°减少到0.013°。显然，基于位姿闭环反馈的机器人末端位姿补偿方法具有很好的收敛性和较高的位姿补偿效率。

(a)位置误差

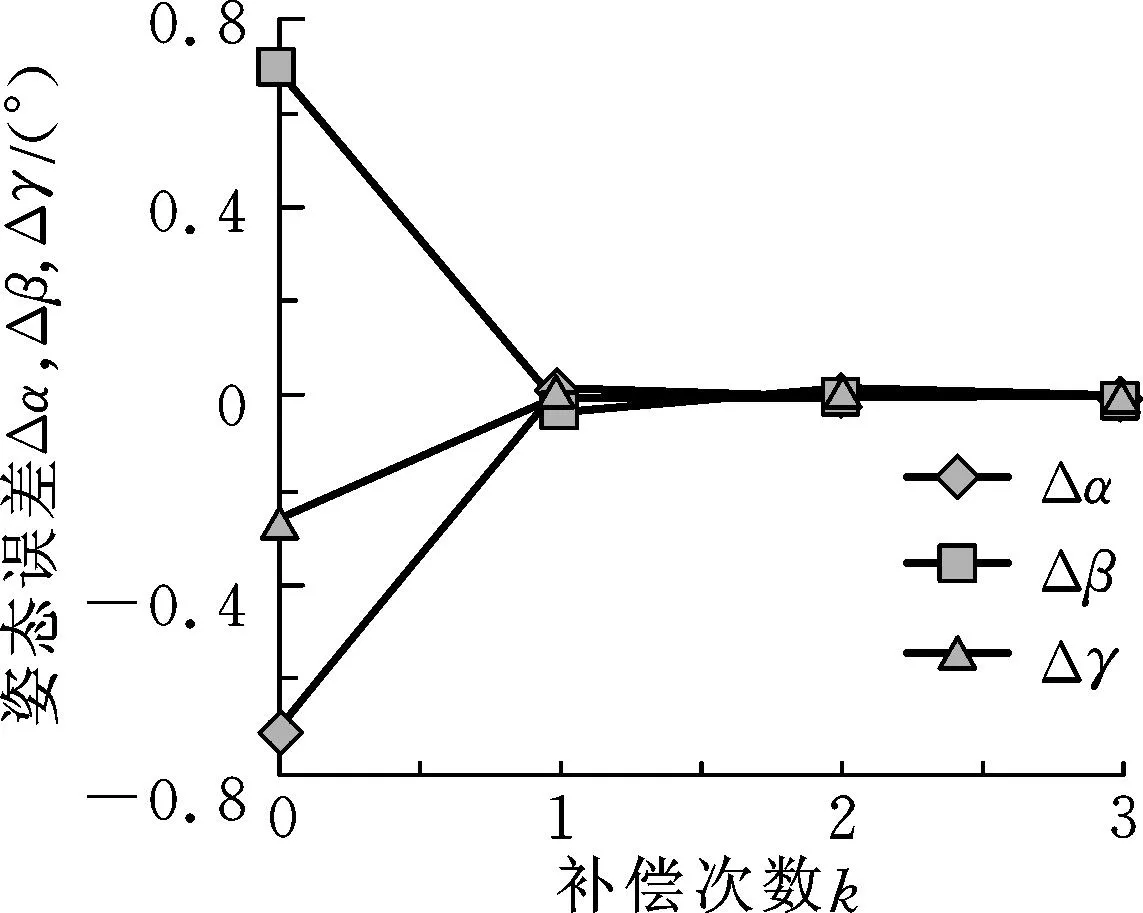
(b)姿态误差图4　机器人位姿补偿过程

(a)位置误差

(b)姿态误差图5　机器人位姿定位精度比较

(a)位置误差

(b)姿态误差图6　机器人位姿重复定位精度比较

实验中，为了获得经过位姿闭环反馈补偿后的机器人的定位精度和重复定位精度，对于每一个参考位姿，重复多次从同一个方向对机器人的位姿进行补偿和定位，记录每次机器人最终实际定位位姿与参考位姿的偏差值。然后计算位姿偏差的均值作为位姿闭环反馈系统的定位精度，同时计算位姿偏差的标准差作为位姿闭环反馈系统的重复定位精度。最后，对工业机器人在位姿反馈补偿前后位姿定位精度和重复定位精度进行比较。图5是工业机器人补偿前后的位姿定位精度对比图，图中横坐标为对应的参考位姿编号。从图中可以非常明显地看出，经过位姿闭环反馈补偿后，工业机器人的末端位姿精度得到了明显的提高。总体来说，经过补偿后工业机器人的末端位置误差可降低到0.09 mm以下，最大幅度可降低到0.05 mm，姿态误差降低0.015°以下,最大幅度可降低到0.012°。相比于补偿前，机器人末端位置误差最大幅度降低95%，姿态误差降低92%。图6是工业机器人补偿前后的位姿的重复定位精度对比图，图中横坐标为对应的参考位姿编号。从图中可以看出，经过位姿补偿后，工业机器人的重复定位精度也有了很大的提高，其中位置误差从补偿之前的0.08～0.14 mm降低到了0.02～0.05 mm，姿态误差从补偿之前的0.015°～0.03°降低到了0.003°～0.005°。显然，实验结果证明，本文提出的基于位姿闭环反馈的工业机器人定位补偿方法可以同时显著提高机器人的绝对定位精度和重复定位精度。

4　结论

本文提出了一种基于末端位置和姿态闭环反馈的工业机器人绝对定位补偿方法。该方法使用激光跟踪系统来测量机器人末端上的靶标点来获得机器人的当前位姿，并通过与靶标点的理论位置匹配来计算机器人末端位姿偏差。工业机器人则根据位姿偏差数据对末端的位姿进行修正。激光跟踪测量系统与机器人系统通过工业局域网和OPC服务进行数据通信。最后通过实验验证了基于位姿闭环反馈的机器人绝对定位补偿方法的有效性，实验结果证明该方法可以显著降低工业机器人的定位误差。

[1]邾继贵，邹剑，林嘉睿，等.面向测量的工业机器人定位误差补偿[J]. 光电子激光，2013，24(4):746-750.

Zhu Jigui，Zou Jian，Lin Jiarui，et al. Measurement-oriented Positioning Error Compensation for Industrial Robot[J]. Journal of Optoeletronics Laser，2013，24(4):746-750.

[2]Elatta A Y，Li Peigen，Fan Liangzhi,et al. An Overview of Robot Calibration[J]. Information Technology Journal，2004 3(1):74-78.

[3]Renders J M，Rossignol E，Becquet M,et al. Kinematic Calibration and Geometrical Parameter Identification[J]. IEEE Transaction on Robotics and Automation，1991，7(6)：721-732.

[4]Veitschegger W K，Wu C H. Robot Accuracy Analysis Based on Kinematics[J]. IEEE J. Robotics Automat，1986，2(3)：171-180.

[5]Veitschegger W K，Wu C H. Robot Calibration and Compensation[J]. IEEE J. Robotics Automat，1988,4(6)：643-656.

[6]Denavit J,Hartenberg R S. A Kinematic Notation for Lower-pair Mechanisms Based on Matrices[J]. ASME Journal of Applied Mechanics，1955，22:215-221.[7]刘振宇,陈英林,曲道奎,等.机器人标定技术研究[J].机器人，2002，24(5)：447-450.

Liu Zhenyu, Chen Yinglin, Qu Daokui,et al. Research on Robot Calibration. Robot,2002, 24(5):447-450.

[8]王东署.工业机器人标定技术研究[D].沈阳：东北大学，2006.

[9]任永杰,邾继贵,杨学友,等.利用激光跟踪仪对机器人进行标定的方法[J].机械工程学报，2007，43(9):195-200.

Ren Yongjie, Zhu Jigui, Yang Xueyou,et al. Method of Robot Calibration Based on Laser Tracker[J]. Chinese Journal of Mechanical Engineering,2007,43(9): 195-200.

[10]Sunnanbo A. Laser Feedback Control for Robotics in Aircraft Assembly[D]. Ostergotland，Sweden：Linkopings University，2003.

[11]Gonzalez-galvan E J，Cruz_Ramirez S R，Seelinger M J，et al. An Efficient Multi-camera，Multi-target Scheme for the Three-dimensional Control of Robots Using Uncalibrated Vision[J]. Robotics and Computer-integrated Manufacturing，2003，19(5):387-400.

[12]Olsson T，Mathias H，Henrik K，et al. Cost-efficient Drilling Using Industrial Robots with High-band-width Force Feedback[J]. Robotics and Computer-integrated Nanufacturing，2010，26(1):24-38.

[13]Wang Z，Maropolous P G. Real-time Error Compensation of a Three-axis Achine Tool Using a Laser Tracker[J]. The International Journal of Advancedmanufacturing Technology，2013，69(1/4):919-933.

[14]Vincze M，Prenninger J P，and Gander H. A Laser Tracking System to Measure Position and Orientation of Robot End Effectors under Motion[J]. The International Journal of Robotics Research，1994，13(4):305-314.

[15]Arun K S，Huang T S，Blostein S D. Least-squares Fitting of Two 3-D Point Sets[J]. Pattern Analysis and Machine Intelligence，IEEE Transactions on，1987 5(9)：698-700.

[16]Horn B K P. Closed-form Solution of Absolute Orientation Using Unit Quaternions[J]. JOSA A，1987，4(4)：629-642.

(编辑郭伟)

Positioning Error Compensation Method of Industrial Robot Based on Closed-loop Feedback of Position and Orientation

He Qingxi1You Zhenzhou1Kong Xiangdong2

1.Wenzhou Vocational & Technical College，Wenzhou，Zhejiang，325000 2.Wenzhou University Oujiang College，Wenzhou，Zhejiang，325000

In order to improve the absolute positioning accuracy of an industrial robot，a position compensation method was proposed herein based on closed-loop feedback of the position and orientation of the end effector. The compensation utilized a laser tracker to monitor the position and orientation of the robot，by measuring the optical tooling points (OTPs) fixed on the end effector，and calculated the deviations of the position and orientation by registering nominal coordinates and the measured coordinates of the OTPs. The industrial robot system communicated with the laser tracker system by industrial LAN，and adjusted the position and orientation of the robot according to the deviation data. The experiments attached in end verified the compensation method，which shows that the location errors are reduced to 0.05 mm in maximum，and the orientation errors are reduced to 0.012 degree in maximum.

industrial robot；absolute positioning accuracy；closed-loop feedback of position and orientation；laser tracker

2015-05-23

国家高技术研究发展计划(863计划)资助项目(2011AA04A101)

TP202;TH242DOI：10.3969/j.issn.1004-132X.2016.07.004

何庆稀，男，1972年生。温州职业技术学院机械工程系副教授。主要研究方向为机械优化设计、CAD/CAM及工业机器人。游震洲，男，1969年生。温州职业技术学院机械工程系副教授。孔向东，女，1965年生。温州大学瓯江学院教授级高级工程师。