非均质中低分辨率像元土壤含水量地面采样方法研究进展

王春梅，占玉林，魏香琴，李娟，李玲玲，刘苗

（中国科学院 遥感与数字地球研究所，北京，100101）

非均质中低分辨率像元土壤含水量地面采样方法研究进展

王春梅，占玉林，魏香琴，李娟，李玲玲，刘苗

（中国科学院 遥感与数字地球研究所，北京，100101）

在一定的精度条件下，如何通过合理的地面采样方法获取非均质混合像元的地面真值，是遥感准确反演土壤含水量需要解决的基本问题。目前常用的地面传统采样方法包括传统统计采样、自助采样、随机组合采样、地统计采样、分层采样、稳定性采样，都需要地面较密集的实测数据才能获得合理的采样方案，然而，在实际中，中低分辨率尺度很难进行地面预采样，传统地面采样方法很难满足区域尺度土壤含水量的地面采样需求。基于先验知识的地面采样方法由于不需要地面较密集的实测数据，已成为中低分辨率像元土壤含水量地面采样的新热点。综合分析土壤含水量不同地面采样方法的特点和优势以及采样方法的适用条件，为土壤含水量反演算法模型的构建和产品的真实性检验提供科学的地面采样参考依据。

土壤含水量；非均质；采样

土壤含水量是水文模型、气候预测模型以及干旱监测模型中重要的参数之一［1-5］。遥感是获取生产区域与全球土壤含水量的主要手段，近年来，基于AMSR-E和SMOS等被动微波卫星遥感数据，生产了全球土壤含水量产品［1， 6］，另外，2015年计划发射的土壤水分主、被动微波卫星（SMAP）也将为土壤含水量产品的生产提供新的数据源［7-10］。无论是土壤含水量反演算法模型的构建还是产品的真实性检验，都需要通过地面仪器获得实测土壤含水量［11-15］。但目前土壤含水量的地面采样研究工作严重滞后，特别是对非均匀地表特性的尺度转换研究滞后，这使得区域尺度的遥感信息与田间尺度的地表观测信息脱节，进而制约着土壤含水量定量遥感产品在相关领域更好地推广与应用。土壤含水量具有较大的时空变异，尤其是表层土壤含水量变化剧烈［16-17］，这就要求在土壤含水量定量遥感产品模型构建和地面检验时，必须对地面实测数据实时同步进行，这导致对土壤含水量的地面采样存在困难。因此，在一定的精度条件下，如何通过合理的地面采样方法获取非均质混合像元的地面真值，是遥感准确反演土壤含水量需要解决的基本问题，这对于定量遥感产品的模型构建和地面真实性检验均具有十分重要的意义。迄今为止，众多学者探讨了土壤含水量地面采样的策略问题。一个准确的样本设计方案应保证样本点的均值是对像元总量均值进行很好估计［18-19］。合理取样数目取决于土壤含水量样本总量的变异性、估计像元总量均值所要求的精度、估计像元总量均值所需的置信区间、地面采样的费用等。在过去的几十年里，已建立多种土壤含水量地面采样方法，本文将其归纳为统计特征采样、时空格局采样和先验知识采样，重点对土壤含水量地面采样方法的国内最新研究进展进行分析，总结常用地面采样方法的特点和优势，并探讨不同采样方法的适用条件。

1　基于土壤含水量样本数据统计特征的地面采样

1.1传统统计采样

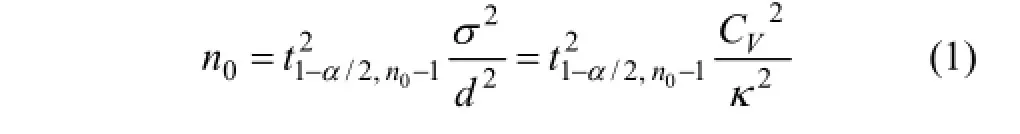
在地学研究中，目前应用最多的是传统统计方法［20-24］，同时，也是遥感反演常用的地面采样方法，即根据像元内的变异程度，估计像元内的合理取样数目。当像元内土壤含水量样本数据相互独立且满足正态分布时，可用下面公式估计一定误差水平下所需的地面合理取样数目（n0）［14］：式中：σ为标准差；t1-α/2为一定置信水平 LC即（1-α）下的t分布特征值；，为绝对误差，μ为像元内总体的真实平均值，为像元内n个样本的平均值；κ=d/μ，为相对误差。由于土壤含水量在不同位置、不同时间的CV比σ稳定得多［14］，因此，当难以获取有效的σ时，可利用CV和κ来估算n0。在一定精度下，传统统计计算的合理取样数目与变异系数的平方成正比［15-16］。但传统统计方法具有局限性，必须满足像元内土壤含水量样本数据的正态分布及样点之间的空间独立［25］。当违背这一条件时，传统方法得到的合理取样数目与实际需要不符［26］。

传统统计方法仅能估算像元内土壤含水量的取样数目，但没有考虑样点的空间布局，而实际中样点空间布局对最终的采样结果有很大的影响。科研人员通常采用已有的样点布局模式，包括栅格采样、随机采样、均匀采样等，但这些方法要么费时费力，要么对抽样精度有很大的影响。

1.2自助方法采样

近20年来，一种新的方法——自助法（bootstrap）逐渐用于土壤含水量的地面采样设计。这种方法是当今流行的地面数据重采样方法，不受数据分布特征的限制［8］。

若某像元内有n个表层土壤含水量的地面观测值θi（i=1，2，…，n），当n足够大时，像元的平均含水量可以认为是这n个实测含水量的平均值。自助法不受样本统计分布的局限，可通过对n个观察值的重复抽样模拟得到接近真实的样本分布特征［27］。应用自助法确定采样策略的基本思路如下：

1） 从像元内所有实测数据 n中分别随机选出 m个数据（m=1，2，3，…，n），每次选择随机重复B次。

2） 计算每次选择得到的m个样本均值，共获得B个样本均值。

3） 分别计算B个均值与全部n个实测样点均值之间的相对误差，分析相对误差在5%或10%内的置信水平LC。

4） 绘制置信水平LC与样本数目m的关系图，从而确定一定LC（95%或90%）下对应的合理取样数目。

MANLY［28］建议自助采样实际应用中的B应不少于1 000次，有时甚至需要设置10 000次。然而，为了避免冗长的计算时间，很多研究者在实际应用中尽量选择小的样本数目（n）或者少的重复数（B）［29-30］。但即使样本数目n很小，1 000次甚至10 000次的重复数B也很难覆盖所有的组合数，如当n=20和m=10时，从n个数据中随机选择m个数据共存在的组合数有个，此时设置较小的B（＜184 756）势必会导致样本数目置信水平不稳定［29］。更重要的是，自助法的采样效率并不高于传统统计采样效率，这也是限制自助法在遥感地面采样应用的关键原因［16］，而且这种方法也没有考虑样点的空间布局。

1.3随机组合采样

为了发挥自助方法优势，针对自助方法存在的精度不稳定和采样效率低等问题，提出利用随机组合地面采样估算像元内的土壤含水量地面合理取样数目［31］。这种方法的改进之处在于将所有的组合数目）代替固定重复次数 B，以 s个平均值代替 B个平均值，其余步骤则与自助法的相同。

随机组合方法不需要传统统计和分层采样所要求的数据独立和正态分布前提，也不需要地统计学采样方法的半方差函数信息，因此，随机组合方法的实际应用范围更广，而且与传统统计、地统计、分层采样和自助采样相比，随机组合方法提供了合理有效的采样策略。在相同的精度要求下，随机组合方法估算的合理取样数目要远比传统统计和自助采样的数目少［21］。然而，随着像元分辨率的降低，土地利用类型多样，地形地势复杂，土壤含水量势必具有更高的时间变异和空间变异，这意味着随机组合方法需要有地面更密集的实测土壤含水量数据才能获得合理的采样方案。但随着实测样点的增加，尤其当变异系数较大或观测数据较复杂时，随机组合计算结果往往会消耗较长的时间，而且这种方法也没有考虑样点的空间布局。

2　基于土壤含水量样本数据时空变异的地面采样

2.1地统计采样

地统计学考虑了像元内土壤含水量的空间变异和空间相关，克服了样点独立的局限，能较好地估算合理取样数目。

由于遥感像元尺寸通常是正方形（S），像元可被看成由观测点在中心、边长等于采样间隔的n个正方形组成，将n作为采样数目。此时，每个采样块S的土壤含水量平均值的估算方差式中：为像元S内中心点x和其他所有点之间的平均半方差值为像元S内所有点之间的平均半方差值。若像元 S的估计值为θSi（i=1，2，…，n），则像元均值表示为，相应的全局估计方差为［22］

根据式（2）和（3），可以从标准误差和采样数目的关系图中得到一定误差水平下的合理取样数目［23］。

研究表明，土壤含水量在一定范围内存在空间自相关性［34-35］。地统计采样克服了地面样点独立的局限性，考虑了土壤含水量的变异结构对实际采样的影响。JACOBS等［22］较早讨论了应用地统计学理论确定土壤pH合理取样数目的方法，此后许多研究者也用该方法研究了不同土壤参数的空间变异及采样设计［36］，均认为地统计学方法比传统统计方法在设计采样方案时更有效，能用较少数目的样品获得同样精度的估值。

但在地统计采样过程中必须准确获取像元内土壤含水量的空间变异函数，需要更高分辨率的数据或者进行像元预采样获取较准确的变异函数。

2.2区域分层采样

ORLÓCI［37］提出一个生态系统的表征必须考虑其内部的变异特征。而分层采样满足此要求。分层采样可以有效地提高土壤含水量总体估计值的精确度，是最精确的取样策略方法之一。分层抽样研究已用于人口普查、环境分析、产品测试以及土壤科学等不同领域［38-39］。

在像元土壤含水量分层采样中，将像元大小为M的总体分成 L个不相重叠的层，它们的大小分别为M1，M2，…，ML。第q（q=1，2，…，L）层的权重为Wq=Mq/ M，可认为是第q层面积占整个像元面积的比例［29］。分层采样的总体估计均值是 L个样本均值θq的加权平均，和θst的方差分别为：

式中：σq，nq和fq=nq/ Mq分别为第q层的标准差、样本数目和抽样比。若数据满足正态分布，在1-α的置信水平下，（d/Z1-α/2）2可代替式（5）中的，则所有层的合理取样数目可表示为

分层采样除了能确定像元内总的合理取样数目（n0）外，还能进一步估计像元内各单元层的取样数目。第q层的取样数目为

虽然分层采样精度较高，能有效地减少取样时间和降低取样成本，但也受到一些条件的限制。例如，一方面精度受分层方式的影响，另一方面必须有进行像元分层的先验资料支持，若按土壤类型对非均质中低分辨率像元进行分区，则首先必备土壤质地分类图［23］；若按土地利用类型进行分区，则必须有试验区域详细的土地利用分类图［40］。总之，在分层取样之前，需要试验区域的部分先验数据和资料对其进行分层，这在实际调查中工作量较大。

2.3时间稳定性采样

土壤含水量随时间和空间地理位置的变化而变化，但当把土壤含水量按大小排序或与平均含水量进行比较时，空间变异格局表现出随时间持续不变的特性，这种现象叫时间稳定性，这些样点就是时间稳定性点［41］。若在某种尺度下存在土壤水分时间稳定性点，则可根据时间稳定性点土壤水分含量与研究区域的平均土壤水分含量的关系，估计和预测研究区域的平均土壤水分状况，这样将大大简化估算某个研究区域平均土壤水分状况的采样和测定工作，可广泛用于遥感土壤水分验证和农田土壤水分监测与管理［42］。

不同位置间的变异性可利用地统计理论进行分析，而不同样点位置随时间的变化则可用时间稳定性来表征［33］。在分析试验区的稳定样点之前，首先利用斯皮尔曼等级（Spearman rank）相关系数rs验证稳定位置的存在性：

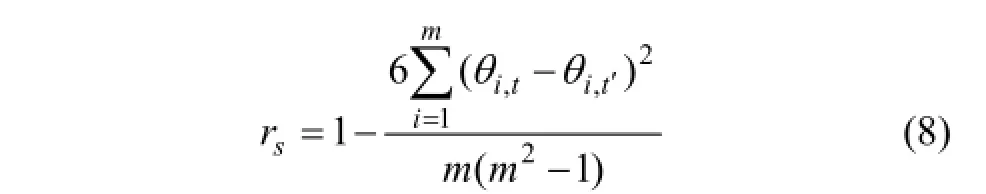
式中：m为土壤含水量对应的观测数目；θi，t（或θi，t′）为位置i处的土壤含水量观测值在t（或t′）时刻的等级。rs越接近1，则观测值在时期t和t′的稳定性越大。

经过分析确认稳定位置后，下一步需要确定具体的样本位置。假定t时刻（t=1，2，…，nt）土壤含水量的均值为

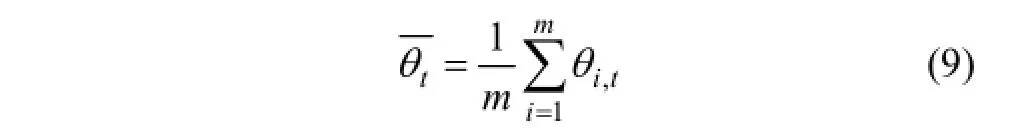
因此，每个样本点的平均相对误差δi和相对误差的方差为：

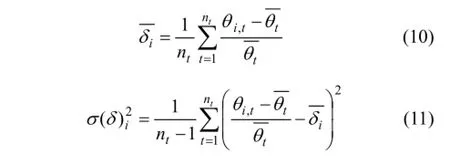
每个样本的相对误差表征此位置相对像元平均含水量的干湿程度，而方差能较好地表征测量精度。为了有效地减少系统偏差和准确地捕捉不同采样时间的田块均值，应综合考虑均值和方差，因此，利用根均方差（ERMS）确定最佳的稳定样本位置：

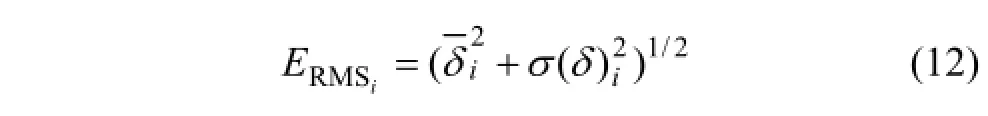
时间稳定采样是基于前期大量土壤含水量实测值，筛选代表性测点非常繁琐。一般来说，在测量周期内需测定 13～15次，才能获得较准确的结果。

3　基于土壤含水量主控因子先验知识的地面采样

在遥感验证观测试验中，通常对实验区的背景知识（植被分布、地形高程、土壤质地等）有一定认识。随着大型验证观测项目的开展，逐渐发展了基于先验知识的采样方法，这种方法是基于由相关先验知识获取的多元辅助变量进行的优化分区进行的样点布设。根据各样区内部空间异质性和样区间的相关性进行统计分析，构建优化的主控因子先验知识样本布设方案。土壤含水量是众多环境因素共同作用的结果，包括地形、植被类型、土壤类型、降雨量等，土壤含水量的地面采样需要考虑主要影响因子。目前已有文献报道关于土壤含水量稳定性测点与影响因素的关系分析，如：WANG等［43］在山东省非耕地面积的抽样调查中，证实了在空间相关性较强的地区，有先验知识的采样方式具有更高的采样效率；曹志冬等［44］比较了地理空间对象中不同先验知识抽样方式的分层效率，指出有效的采样方法会降低样本点的不确定性；高磊［45］利用土壤属性和海拔因子预测土壤含水量稳定性采样测点。贾玉华等［46］引入植被类型/土层深度、土壤质地分析土壤含水量的稳定性。曾也鲁等［12］提出了基于NDVI 植被指数先验知识的LAI采样方法，并指出这种方法对非均质特性较明显的区域具有较高的精度和较强的稳定性。基于先验知识指导的采样法已经成为目前采样效率较高且应用广泛的采样方法，尤其是采样区的空间相关性越强，先验知识越丰富，知识分层的地面采样效果越显著［44］。但是，这类研究工作大多是基于单一环境因子或多环境因子对代表性测点的简单相关或回归统计，多限于变化趋势性的表面观测，有关土壤含水量稳定性测点与土壤质地、植被类型及地形因子等不同影响因素的综合研究较少，尤其缺少对土壤含水量稳定性测点的定量研究。

4　结论

1） 将非均质中低分辨率像元的土壤含水量地面采样方法分为3类：基于样本数据统计特征的地面采样、基于样本数据时空格局的地面采样和基于主控因子先验知识的地面采样。

2） 基于样本数据统计特征的地面采样和基于时空格局的地面采样几乎都需要地面较密集的实测土壤含水量或者掌握土壤含水量较准确的变异程度，才能获得合理的地面采样方案。

3） 基于先验知识的地面采样方法不需要地面较密集的实测土壤含水量，将成为一个重要的研究内容和发展方向。由于土壤含水量的影响因素极其复杂，必须深入研究土壤含水量稳定性测点与土壤质地、植被类型及地形因子等不同影响因素的定量关系，才能建立先验知识的合理、高精度地面采样。

4） 被动微波作为目前比较成熟的遥感手段将越来越普及。未来土壤含水量遥感产品的地面采样方法应该更多地解决无地面实测数据区域的地面采样问题，使采样方法更加具有实用性，使其更好地服务于土壤含水量反演算法的精度验证和产品的真实性检验。

［1］ NARAYAN U， LAKSHMI V， NJOKU E G. Retrieval of soil moisture from passive and active L/S band sensor （PALS）observations during the soil moisture experiment in 2002 （SMEX02）［J］. Remote Sensing of Environment， 2004， 92：483-496.

［2］ CHAHINE T M. The hydrological cycle and its influence on climate［J］. Nature， 1992， 359： 373-380.

［3］ MILLY P C， DUNNE K A. Sensitivity of the global water cycle to the water-holding capacity of land［J］. Journal of Climate，1994， 7： 506-526.

［4］ BALSAMO G， VITERBO P， BELJAARS A， et al. A revised hydrology for the ECMWF model： Verification from field site to terrestrial water storage and impact in the integrated forecast system［J］. Journal of Hydrometeorol， 2009， 10（6）： 623-643.

［5］ DRUSCH M， HOLMES T， DEROSNAY P， et al. Comparing ERA-40-based l-band brightness temperatures with sky lab observations： calibration/validation study using the community microwave emission model［J］. Journal of Hydrometeorol， 2009，10（4）： 213-226.

［6］ PARINAZ R， AARON A B， CATHERINE C， et al. Estimation of soil moisture using optical/thermal infrared remote sensing in the Canadian Prairies［J］. ISPRS Journal of Photogrammetry and Remote Sensing， 2013， 83： 94-103.

［7］ BINDLISH R， CROW W T， JACKSON T J. Role of passive microwave remote sensing in improving flood forecasts［J］. IEEE Geoscience and Remote Sensing Letters， 2009， 6（1）： 112-116.

［8］ ZHENG W， LIU C， XIN Z， et al. Flood and waterlogging monitoring over Huaihe River basin by AMSR-E data analysis［J］. Chinese Geographical Science， 2008， 18（3）： 262-267.

［9］ 施建成， 杜阳， 杜今阳， 等. 微波遥感地表参数反演进展［J］.中国科学：地球科学， 2012， 42（6）： 814-842. SHI Jiancheng， DU Yang， DU Jinyang， et al. Progresses on microwave remote sensing of land surface parameters［J］. Science China Earth Science， 2012， 55： 1052-1078.

［10］ BROCCA L， MORAMARCO T， MELONE F， et al. Assimilation of surface and root-zone ASCAT soil moisture products into rainfall-runoff modelling［J］. IEEE Transactions on Geoscience and Remote Sensing， 2011， 99： 1-14.

［11］ 曾也鲁， 李静， 柳钦火. 全球 LAI地面验证方法及验证数据综述［J］. 地球科学进展， 2012， 27（2）： 165-174. ZENG Yelu， LI Jing， LIU Qinhuo. Review article： global LAI ground validation dataset and product validation framework［J］. Advances in Earth Science， 2012， 27（2）： 165-174.

［12］ 曾也鲁， 李静， 柳钦火. 基于NDVI先验知识的LAI地面采样方法［J］. 遥感学报， 2013， 17（1）： 114-121. ZENG Yelu， LI Jing， LIU Qinhuo. A sampling strategy based on NDVI prior knowledge for LAI ground measurements［J］. Journal of Remote Sensing， 2013， 17（1）： 107-121.

［13］ JACOBS J M， MOHANTY B P， HSU E， et al. SMEX02： field scale variability，time stability and similarity of soil moisture［J］. Remote Sensing of Environment， 2004， 92： 436-446.

［14］ DE LANNOY G J M， VERHOEST N E C， HOUSER P R， et al. Spatial and temporal characteristics of soil moisture in an intensively monitored agricultural field （OPE3）［J］. Journal of Hydrology， 2006， 331： 719-730.

［15］ QIN J， YANG K， LU N， et al. Spatial upscaling of in-situ soil moisture measurements based on MODIS-derived apparent thermal inertia［J］. 2013， 138： 1-9.

［16］ HUPET F， VANCLOOSTER M. Intraseasonal dynamics of soil moisture variability within a small agricultural maize cropped field［J］. Journal of Hydrology， 2002， 261： 86-101.

［17］ LOAGUE K. Soil water content at R-5，1：Spatial and temporal variability［J］. Journal of Hydrology， 1992， 139： 233-251.

［18］ ASTM. Standard guide for general planning of waste sampling［S］.

［19］ WANG X J， QI F. The effects of sampling design on spatial structure analysis of contaminated soil［J］. The Science of the Total Environment， 1998， 224： 29-41.

［20］ TREASURER J W， POPE J A. Selection of host sample number and design of a monitoring programme for ectoparasitic sea lice （Copepoda： Caligidae） on farmed Atlantic salmon［J］. Salmo Salar， Aquaculture， 2000， 187： 247-260.

［21］ YIM M H， JOO S J， SHUTOU K， et al. Spatial variability of soilrespiration in a larch plantation： estimation of the number of sampling points required［J］. Forest Ecology and Management，2003， 175： 585-588.

［22］ JACOBS J M， MOHANTY B P， HSU E， et al. SMEX02：field scale variability，time stability and similarity of soil moisture［J］. Remote Sensing of Environment， 2004， 92： 436-446.

［23］ MIYAMOTO S， CHACON A， HOSSAIN M， et al. Soil salinity of urban turf areas irrigated with saline water： I. spatial variability［J］. Landscape and Urban Planning， 2005， 71：233-241.

［24］ GILBERT R O. Statistical methods for environmental pollution monitoring［M］. New York： Van Nostrand Reinhold Company Inc， 1987， 26-54： 17-52.

［25］ HUPET F， VANCLOOSTER M. Sampling strategies to estimate field real evapotranspiration fluxes with a soil water balance approach［J］. Journal of Hydrology， 2004， 292： 262-280.

［26］ WARRICK A W. Soil water dynamics［M］. New York： Oxford University Press， 2003： 100-101.

［27］ EFRON B， TIBSHIRANI R J. An introduction to the bootstrap：monographs on statistics and applied probability［M］. New York： Chapman & Hall Press， 1993： 66-68.

［28］ MANLY B F J. Randomization， bootstrap and Monte Carlo methods in biology［M］. 2nd ed. London： Chapman & Hall Press，1997： 56-60.

［29］ DANE J H， REED R B， HOPMANS J W. Estimating soil parameters and sample size by bootstrapping［J］. Soil Science Society of America Journal， 1986， 50： 283-287.

［30］ KAMGAR A， HOPMANS J W， WALLENDER W W， et al. Plot size and sample number for neutron probe measurements in small field trials［J］. Soil Science， 1993， 156： 213-224.

［31］ WANG C M， QIANG Z， ZHANG R. Estimating the necessary sampling size of surface soil moisture at different scales using a random combination method［J］. Journal of Hydrology， 2008，352： 309-321.

［32］ MCBRATNEY A B， WEBSTER R. How many observations are needed for regional estimation of soil properties［J］. Soil Science，1983， 135： 177-183.

［33］ CHUNG C K， CHONG S， VARSA E C. Sampling strategies for fertility on a stony silt loam soil［J］. Communication of Soil Science and Plant Analysis， 1995， 26： 741-763.

［34］ DE ROOIJ H， STAGNITTI F. Spatial variability of solute leaching： experimental validation of a quantitative parameterization［J］. Soil Science Society of America Journal，2000， 64： 499-504.

［35］ PACHEPSKY Y， RADCLIFFE D， SELIM H M. Scaling methods in soil physics［M］. New York： CRC Press LLC， 2002：102-103.

［36］ DE ROOIJ G H， STAGNITTI F. Spatial variability of solute leaching： experimental validation of a quantitative parameterization［J］. Soil Science Society of America Journal，2000， 64： 499-504.

［37］ ORLÓCI L. Community organization： recent advances in numerical methods［J］. Canadian Journal of Botany-Revue Canadienne de Botanique， 1988， 66： 2626-2633.

［38］ PARK S J， VAN D E GIESEN N. Soil-landscape delineation to define spatial sampling domains for hillslope hydrology［J］. Journal of Hydrology， 2004， 295： 28-46.

［39］ CATHERINE A， TROUSSELLIER M， BERNARD C. Design and application of a stratified sampling strategy to study the regional distribution of cyanobacteria（Ile-de-France， France）［J］. Water Research， 2008， 42： 4989-5001.

［40］ PETERSEN R G， CALVIN L D. Sampling： methods of soil analysis. I： physical and mineralogical methods［M］. WI：American Society of Agronomy， Soil Science Society of America， 1986： 100-104.

［41］ VACHAUD G， PASSERAT D E， SILANS A， et al. Temporal stability of spatial measured soil water probability density function［J］. Soil Science Society of America Journal， 1985， 49：822-828.

［42］ HU W， SHAO M A， REICHARDT K. Using a new criterion to identify sites for mean soil water storage evaluation［J］. Soil Science Society of America Journal， 2010， 74： 762-773.

［43］ WANG J F， HAINING R， CAO Z D. Sample surveying to estimate the mean of a heterogeneous surface： reducing the error variance through zoning［J］. International Journal of Geographical Information Science， 2010， 24（4）： 523-543.

［44］ 曹志冬， 王劲峰， 李连发， 等. 地理空间中不同分层抽样方式的分层效率与优化策略［J］. 地理科学进展， 2008， 27（3）：152-160. CAO Zhidong， WANG Jinfeng， LI Lianfa， et al. Strata efficiency and optimization strategy of stratified sampling on spatial population［J］. Progress in Geography， 2008， 27（3）： 152-160.

［45］ 高磊. 黄土高原小流域土壤水分时间稳定性及空间尺度性研究［D］. 北京： 中国科学院教育部水土保持与生态环境研究中心， 2012： 40-55. GAO Lei. Temporal stability and the spatial scaling of soil moisture in a small watershed on the Loess Plateau［D］. Beijing：Chinese Academy of Sciences and Ministry of Education. Research Center of Soil and Water Conservation and Ecological Environment， 2012： 40-55.

［46］ 任婷婷， 王瑄， 陈雯静， 等. 不同土地利用类型土壤颗粒分形特征与粘粒含量的关系［J］. 沈阳农业大学学报， 2013， 44（2）：202-207. REN Tingting， WANG Xuan， CHEN Wenjing， et al. Relationship of soil particles fractal characteristics and clay content under different land use ways［J］. Journal of Shengyang Agricultural University， 2013， 44（2）： 202-207.

（编辑 陈灿华）

Ground sampling strategy for surface soil moisture in heterogeneous remote sensing pixels

WANG Chunmei， ZHAN Yulin， WEI Xiangqin， LI Juan， LI Lingling， LIU Miao

（The Institute of Remote Sensing and Digital Earth， Chinese Academy of Sciences， Beijing 100101， China）

The most important question is how to select reasonable ground sampling method to obtain the mean soil moisture within the mixed pixels. Some traditional sampling methods， including traditional statistical sampling，self-sampling， random sampling， geostatistical sampling， stratified sampling and temporal stability， all need to be more intensive ground measured data in order to obtain a reasonable sampling plan. However， in practice， it is very difficult to make the ground pre sampling in the regional scale， so the traditional sampling methods can hardly meet the requirement of the soil moisture monitoring. In recent years， the priori knowledge ground-based sampling method has become a widely used sampling method without the more intensive measured data. The priori knowledge ground soil sampling will be important in future research and development direction. The characteristics， advantages and the applicable conditions of different ground sampling methods were analyzed， which will provide the basis for the construction of the algorithm model and the validation of the soil moisture products.

soil moisture； heterogeneous； sampling

S512.1

A

1672-7207（2016）04-1414-06

10.11817/j.issn.1672-7207.2016.04.043

2015-04-12；

2015-06-14

国家自然科学基金资助项目（41371416）（Project （41371416） supported by the National Natural Science Foundation of China）

占玉林，副研究员，从事生态环境遥感研究；E-mail：zhanyl@radi.ac.cn