基于人工神经网络的发动机点火提前角预测模型

R. F. TURKSON，颜伏伍，2，侯献军，2M. K. A. ALI，4，刘博，2（.现代汽车零部件技术湖北省重点实验室（武汉理工大学），武汉430070；2.汽车零部件技术湖北省协同创新中心，武汉430070；3.现代汽车零部件技术湖北省重点实验室，武汉430070；3.Mechanical Engineering Department，Ho Polytechnic，P. O. Box HP 27，Ghana；4.Automotive and Tractors Engineering Department，Faculty of Engineering，Minia University，6，El-Minia，Egypt）

基于人工神经网络的发动机点火提前角预测模型

R. F. TURKSON1，3，颜伏伍1，2，侯献军1，2M. K. A. ALI1，4，刘博1，2
（1.现代汽车零部件技术湖北省重点实验室（武汉理工大学），武汉430070；2.汽车零部件技术湖北省协同创新中心，武汉430070；3.现代汽车零部件技术湖北省重点实验室，武汉430070；3.Mechanical Engineering Department，Ho Polytechnic，P. O. Box HP 217，Ghana；4.Automotive and Tractors Engineering Department，Faculty of Engineering，Minia University，61111，El-Minia，Egypt）

本文利用人工神经网络建立发动机点火提前角预测模型，提出显式优化神经网络模型复杂度的方法，并提出一种在将实验数据划分为训练、验证和测试数据集前的数据预处理方法，能有效提高模型的精度。得到的最优神经网络模型，对训练、验证、测试数据集预测的相关系数均为1，模型误差几乎为零。在划分数据集前通过复制原始数据集得到大量的数据样本，并通过多次迭代训练（999次），优化的发动机点火提前角预测模型具有很高的精度。

发动机；人工神经网络；点火提前角；预测模型

Richard Fiifi Turkson

武汉理工大学博士在读，主要研究方向为基于智能算法（人工神经网络和遗传算法等）的内燃机建模与性能优化，已发表论文10余篇。

1　前言

人工神经网络是受生物神经系统启发的一种黑箱类建模方法，用于解决现实世界中模式分类、聚类/分类，函数逼近/系统识别，优化和控制系统设计等问题。人工神经网络有较强的并行处理、学习和泛化能力，具有高适应性和容错性等特点；能在一定的精度下，逼近任何函数［1］。因此，近年来受到很多的关注［2，3］，并在汽车发动机领域得到了广泛的运用［4-15］。

Wu等人［4］利用人工神经网络对具有可变气门正时和独立进气排气凸轮轴定相技术发动机的气流进行建模，提出了神经网络模型结构的显式优化方法［5］，该优化方法通过逐步递增模型参数（隐层数量和/或每层的神经元数量），观察训练、验证和测试数据集的均方误差，但是该方法需要有大量的实验数据，才能有较好的预测效果。文献［6］用元模型的方法降低1-D发动机模型的计算复杂度，而不损失有效数据信息，用于快速运行的自控制模型应用。文献［7］基于Levenberg-Marquardt算法，利用人工神经网络对单缸点火发动机的燃料系统识别和燃油喷射定时优化。Hadef等［8］开发了一个人工神经网络模型用来预测可变气门定时小型涡轮增压点火发动机的体积效率，用包含了稳态与瞬态工况的实验数据训练人工神经网络模型，训练模型的具有良好的预测结果。Zhang等［9］利用人工神经网络预测发动机的氮氧化物排放量，用于训练神经网络的输入包括：发动机转速、扭矩和机油温度。在不同发动机工况下，对发动机氮氧化物排放量的模型预测精度很高。在近期的另一项研究［10］中，使用GT-PowerTM 1-D仿真和人工神经网络为点火发动机进行建模，该神经网络结构用贝叶斯规则以及对不同迭代权重进行重新初始化的方法来优化，从而确保了全局收敛性。

本文利用神经网络以发动机转速和进气歧管压力为输入，建立发动机点火提前角预测模型，提出显式优化神经网络模型复杂度的方法，并提出一种新的数据预处理的方法，该方法能在仅有少量数据样本的情况下，得到精度很高的神经网络预测模型。

2　实验设计和建模方法

本研究采用的是改造后以LPG为燃料的上汽通用五菱B15发动机，并用联电LEC4AD发动机管理系统来替代原始管理系统；在配有数据采集系统的AVL交流测功机上测试发动机，试验台架如图1所示。改造后的发动机特征参数如表1所示：表1 实验发动机特征参数

采集发动机在稳态工况下的实验数据，发动机转速范围为400-6000rpm（步长为400rpm），进气歧管压力范围为25kPa- 100kPa（步长为5kPa）。

通过台架实验获得发动机全工况范围内无爆震情况下的点火提前角范围，所得的最小点火提前角为15度，最大点火提前角为44度。在不同工况下，保持发动机转速和进气歧管压力不变，改变点火提起角，并记录发动机最大扭矩输出时的最佳点火提前角。实验数据共240组，图2为基于实验数据的发动机最佳点火提前角MAP图。

2.1神经网络模型误差

神经网络一般由一个输入层，一个输出层以及一个或多个隐层构成，每个层包含若干个神经元。相邻两层的神经元两两相连，前一层神经元的输出作为后一层神经元的输入。每个神经元的所有输入经过权重分配和偏移运算后代入神经元激励函数（一般为非线性函数）中得到该神经元的输出。神经网络能高精度的逼近一个高度非线性函数。

本研究利用神经网络模型进行系统辨识，其主要目的是获取一个能代替原始函数 f的预测函数来估算系统输出，该输出要尽可能接近输入向量X=（x1, x2, x3…，xn）下原始函数 的实际输出y。等式（1）为预测误差（均方根误差）

模型误差E可分解为偏差误差和方差误差两个分量，如等式（2）所示：

其中，Eb=偏差误差，Ev=方差误差

偏差误差的产生是因为预测模型不能完全准确地代替一个复杂的系统，即使神经网络模型的权重和偏差都达到最优，偏差也依然存在。

另一方面，方差误差的产生则由模型的参数数量引起的，并随模型参数的增加而增加。文献［16，17］提出，基于同样的训练样本，模型的参数越少，预测模型相对越精确，这符合精简原则。

对于一个较多样本的训练数据集，方差误差由等式（3）近似得到。

这里，σ2表示方差，n表示参数数量，N表示训练数据样本数量。对于一个训练数据集，方差误差与模型参数数量n成正比。

对于一个高度灵活（多模型参数）的模型，等式（2）中的偏差误差Eb可以被忽略。这样，模型误差的平方就等于方差误差。即：

σ等式（4）表明了训练数据集样本数量N和方差对模型误差的影响［15］。

图3为模型参数、偏差误差和方差误差间的关系，从图3可明显看出，随着模型参数的增加，偏差误差减小，同时方差误差增加。因为，不可能在不恶化（增大）一种误差的前提下，减小（改善）另一种误差。但可以利用多目标优化，实现在偏差误差和方差误差间的折中，从而获得最佳的参数参数数量（最优模型复杂度）。

数据集通常可分为训练数据集和测试数据集。测试数据集用于测试训练得到的神经网络模型的泛化能力。一般来说，模型训练误差大小与偏差误差大小很相近，并随模型参数的增加而减小。测试模型误差为偏差误差和方差误差（模型误差）之和，并在模型参数超过最优模型参数后开始增加。因此，模型参数过少，会导致较高的偏差误差，出现“欠拟合”；而模型参数过多，会导致较大的方差误差出现“过拟合”。为确定最佳的模型参数数量（模型复杂度），可以通过训练大量的模型，并选择对测试数据集预测效果最好的模型为最佳模型。然而这可能会导致“过拟合”，因为模型的选择和评估是基于同样的训练数据集。

解决这个问题的一种方法是引入验证数据集用于选择最佳的模型，本文设置训练、验证、测试样本集的比例为6：2：2。因为在本研究中，优化算法的迭代次数很少，随机选择的初始参数（权重和偏差）基本决定了模型的精度，因此，模型对验证数据集的误差应该作为选择最佳模型的标准。

为了得到最佳的模型复杂度，最重要的一点是通过显式和/或隐式模型复杂度优化方法对偏差和方差误差进行折中。显式方法通过逐步增加模型参数，并观察每种情况下模型的误差。隐式优化方法使用正则化方法，在不改变模型参数的额定数量的情况下改变模型复杂度。

2.2神经网络模型优化方法

本研究利用显式模型复杂度优化方法，逐步增加模型参数（神经元数量），设置模型参数变化范围为6～15个，得到10个不同复杂度的模型。

图4为模型显式优化方法的过程，它包括以下步骤：

步骤1：给定隐层层数和每层神经元数，确定神经网络的结构。神经网络的类型为多层前馈神经网络，使用了双隐层结构，第一个隐层神经元数量固定为15，第二个隐层神经元数量初始值为6（最大为15），输入层神经元数量为2，输出层神经元数量为1。采用随机赋值的方法初始化网络参数（权重和偏差），对不同的隐层采用不同的激励函数。对于15个神经元的和6个神经元的隐层，采用Tansigmoid激励函数，对于只有1个神经元的输出层，使用线性激励函数。

步骤2：使用Leveberg-Marquart［18］算法训练初始神经网络，对步骤1得到的初始网络训练10次，同时观察每次训练的验证误差。

步骤3：如果训练次数小于10次，通过步骤1重新训练，每次训练时，在步骤1中重新初始化网络权重和偏差，直至总的训练次数达到10。

步骤4：选择10次初始训练的神经网络模型中验证误差最小的神经网络模型。选择验证误差作为评价准则是因为，最小验证误差可以实现偏差和误差之间的最佳折中［5，19］。

步骤5：在第二个隐层增加1个神经元数量，以改变神经网络模型的复杂度。

步骤6-8：类似于步骤2-4，重新训练增加隐层神经元数量后的新的神经网络；

步骤9：重复步骤5-8，以获得8个以上的模型，这样就有了10个不同复杂度和验证误差的模型。

步骤10：在这10个不同复杂度的模型中，选择验证误差最小的模型作为最佳的神经网络模型。

上段所述的训练和选择过程在MATLAB®中实现，10种不同复杂度模型中最佳网络模型为2-15-15-1结构。

2.3实验数据处理优化模型性能

在本文研究对象中，有2个输入变量：

转速 和进气歧管压力 ，一个输出变量：最优点火提前角 。等式（5）中的矩阵D表示实验数据，数据中的每一列表示两个输入和一个输出，分别为转速 、进气歧管压力 和最优点火提前角 。N表示整个实验数据样本的数量（240个样本）。

为了优化神经网络的预测精度，本文提出一种新方法来处理数据。传统划分数据集方法是随机选择部分数据作为训练集，剩下的数据样本作为测试集。在这种情况下，训练集和测试集中没有相同的元素，N1（N1=N）代表整个数据集的总数。Shamekhi and Shamekhi［10］提出一种优化的数据集划分方法，将整个数据样本N2（N2=N）划分为训练集和测试集，并使训练集和测试集共享部分样本，如图5中所示：

本文提出一种新的数据集划分方法，在数据集划分之前将N（240）个数据样本复制4次，得到一个总数为5N（1200）的数据集。通过多次复制样本数据，在随机划分数据集时，使得训练、验证、测试（训练、验证、测试集的比例为6：2：2）数据集具有一些相同的样本。同时，根据等式（4），通过复制的方法增加样本总数可以使得减小模型误差。

3　结果和讨论

图6为最佳神经网络模型的训练、验证和测试误差，在优化过程中，使用正则化方法，在不改变模型参数（包括权重和偏差）数量的情况下，优化模型复杂度。在迭代训练一定次数后，正则化方法会在验证误差开始增加时终止训练。

最佳神经网络模型的验证误差为6.56×10-27，迭代次数高达999次，这样就能找到一个全局最优值。由于最佳神经网络模型误差几近为零，因此，训练、验证和测试数据集的相关系数（R）均等于1，如图7所示：

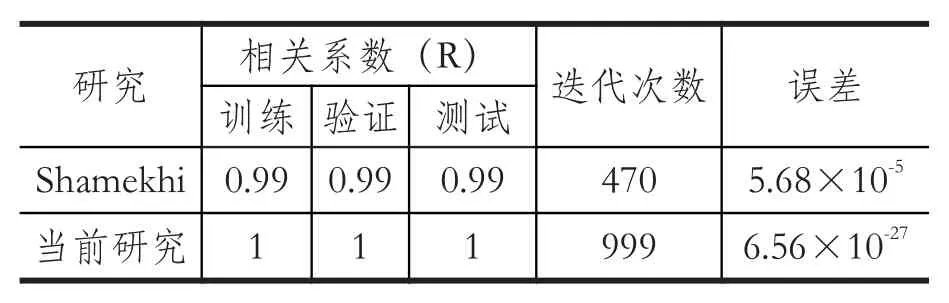
表2　研究结果对比

表2比较了本研究和之前Shamekhi的研究的结果。从表中可以看出，本本研究的训练、验证和测试集相关系数均为1，优于之前Shamekhi的研究结果。在Shamekhi的研究中，迭代次数为470，而在本研究的迭代次数为999，这样可以得到一个更优的神经网络模型。本文选择Shamekhi［10］的研究的结果作为对比，是因为它比其他研究［5，8，9］有更好的预测精度。

4　结论

本研究利用人工神经网络以发动机转速和进气歧管压力作为输入，预测以LPG为代用燃料的发动机的最佳点火提前角，并提出了神经网络模型显式优化方法和一种划分数据集的新方法，以提高神经网络模型的预测精度。该方法有助于实现训练、验证和测试数据的零误差。点火发动机对点火提前角的精度要求很高，预测精度较差的点火提前角预测模型可能经常会引起爆燃，损坏燃烧室以及发动机部件。本研究的模型预测精度很高，能有效避免爆震的发生，仅在发动机的工况发生变化或当燃料质量（在抗爆震性方面）发生变化时，才会发生燃烧爆震。

［1］Leshno，M.，et al.，Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural networks，1993. 6（6）：p. 861-867.

［2］Bhattacharyya，S. and U. Maulik，Soft Computing for Image and Multimedia Data Processing. 2013： Springer.

［3］Jain，A.K.，J. Mao，and K. Mohiuddin，Artificial neural networks： A tutorial. Computer，1996（3）： p. 31-44.

［4］Wu，B.，et al.，Using Artificial Neural Networks for Representing the Air Flow Rate through a 2.4 Liter VVT Engine，2004，SAE International.

［5］Nelles，O.，Nonlinear system identification： from classical approaches to neural networks and fuzzy models. 2001： Springer Science & Business Media.

［6］Papadimitriou，I.，et al.，Neural network based fastrunning engine models for control-oriented applications，2005，SAE Technical Paper.

［7］Yücesan，E.，et al.，Gausslan Radial Basis Functions for Simulation Metamodeling.

［8］El Hadef，J.，et al. Neural Model for Real-Time Engine Volumetric Efficiency Estimation. in 11th SAE International Conference on Engines & Vehicles-ICE2013，Capri： Italie （2013）. 2013.

［9］Zhang，Q.，et al.，Predicting the Nitrogen Oxides Emissions of a Diesel Engine using Neural Networks，2015，SAE Technical Paper.

［10］Shamekhi，A.-M. and A.H. Shamekhi，A new approach in improvement of mean value models for spark ignition engines using neural networks. Expert Systems with Applications，2015. 42（12）： p. 5192-5218.

［11］Wu，B.，et al.，Cam-phasing optimization using artificial neural networks as surrogate modelsmaximizing torque output，2005，SAE Technical Paper.

［12］Wu，B.，et al.，Cam-phasing optimization using artificial neural networks as surrogate models-fuel consumption and NOx emissions，2006，SAE Technical Paper.

［13］杜常清，颜伏伍，杨平龙，等. 基于BP神经网络的发动机转矩估计［J］. 汽车工程，2008，30（7）：588-591.

［14］Sayin，C.，et al.，Performance and exhaust emissions of a gasoline engine using artificial neural network. Applied thermal engineering，2007. 27（1）： p. 46-54.

［15］Kiani，M.K.D.，et al.，Application of artificial neural networks for the prediction of performance and exhaust emissions in SI engine using ethanol-gasoline blends. Energy，2010. 35（1）： p. 65-69.

［16］Forster，M.R.，Key concepts in model selection：Performance and generalizability. Journal of mathematical psychology，2000. 44（1）： p. 205-231.

［17］Foussias，G. and G. Remington，Negative symptoms in schizophrenia： avolition and Occam's razor. Schizophrenia Bulletin，2010. 36（2）： p. 359-369.

［18］Lourakis，M.I.，A brief description of the Levenberg-Marquardt algorithm implemented by levmar. Foundation of Research and Technology，2005. 4： p. 1-6.

［19］Thiery，C. and B. Scherrer. Least-squares λ policy iteration： Bias-variance trade-off in control problems. in International Conference on Machine Learning. 2010.

专家推荐

推荐理由：

文章利用人工神经网络预测发动机最佳点火提前角，详细分析了模型误差产生的原因，提出了模型优化方法，预测模型具有较高的精度。文章条理清晰，具有一定的创新性，并有较好的工程实用价值。

Engine Ignition Advance Timing PredictionModelBased On Artificial Neural Network

R. F. TURKSON1，3，YAN Fu-wu1，2，HOU Xian-jun1，2，M. K. A. ALI1，4，LIU Bo1
（ 1.Hubei Key Laboratory of Advanced Technology for Automotive Components （Wuhan university of technology），Wuhan 430070，China； 2.Hubei Collaborative Innovation Center for Automotive Components Technology，Wuhan 430070，Chian； 3.Mechanical Engineering Department，Ho Polytechnic，P. O. Box HP 217，Ghana； 4.Automotive and Tractors Engineering Department，Faculty of Engineering，Minia University，61111，El-Minia，Egypt ）

An artificial neural network was used in this current study to build the prediction model for engine ignition advance timing.Theprocedure for training and selecting an optimal network structure based on the explicit method of network structure optimization has been presented. The study also presents a novel approach for manipulating limited experimental data before partitioning into training，validation and test data sets for improved prediction accuracy. The results obtained by the proposed method for processing limited experimental data achieved virtually zero errors and a correlation coefficicent of unity for training，validation and testing. The improved prediction accuracy of the selected neural network model was attributed to the larger amount of data resulting from the proposed manipulation of experimental data before partitioning，as well as the comparatively higher （999）training epochs.

engine； artificial neural network； ignition advance timing； prediction model

2016-03-16

TK401

A

1005-2550（2016）04-0056-06

10.3969/j.issn.1005-2550.2016.04.010