基于稳态参数空调器的仿真研究与应用

张抗，杨孝鹏，李灏合肥工业大学建筑设计研究院

基于稳态参数空调器的仿真研究与应用

张抗1，杨孝鹏2，李灏3
合肥工业大学建筑设计研究院

为了提高空调产品的研发效率，节省实验成本，增强产品的理论研究，笔者对空调器进行了计算机仿真。本文主要介绍空调器中压缩机、换热器（冷凝器和蒸发器）、毛细管数学模型的建立与耦合求解。利用MATLAB软件对样机进行了仿真，求算出空调器的制冷剂充注量，毛细管长度，制冷量以及耗功率并与实验结果进行比较，取得了较好的效果。这一方法对空调器设计开发具有参考价值。

空调器；数学模型；仿真；迭代算法；产品设计

引言

近年来，空调系统计算机仿真得到了广泛的发展。空调各组件自身特性研究已经进入了微观领域，葛云亭博士对毛细管内制冷剂流动划分为五个阶段并分别建立了动态分布参数模型，并在国内率先分析了“延迟闪发”对管内制冷及流动的影响[1]。彦启森提出了使蒸发器模型方程封闭可解的界面关系方程,并对该动态参数数学模型所用的偏微分方程进行了离散；在冷凝器建模时考虑到流速不同时冷计侧可能出现不同的流型，建立了针对不同流型的动态方程组[2，3]。陈华俊提出了基于实验数据或者厂家样本数据的变频压缩机图形法模型，并通过修正输气系数提高了图形法模型的通用性[4,5]。

对于系统仿真而言，对于各参数的不同时刻分布并不太关心，而是要求各部件的计算量尽可能小，以满足快速计算的实用化要求。笔者认为，动态分布参数模型不是系统仿真的最佳模型，而稳态参数模型则能满足系统仿真要求。在建立系统各主要部件模型的基础上，以质量平衡，压力平衡，能量平衡为约束条件，使各部件模型有机结合起来构成整个系统的仿真模型。本文介绍空调器设计的算法，即冷凝器过冷度，蒸发器过热度和相关的结构与环境参数为已知条件，以蒸发温度和冷凝温度为迭代变量求解空调器制冷剂充注量、毛细管长度、制冷量和压缩机耗功率。

1　空调器部件仿真模型

部件数学模型包括压缩机模型，冷凝器模型，蒸发器模型和毛细管模型，下文将以R22为制冷剂的风冷式家用空调器为例，分别建立四大部件的仿真模型和充注量计算模型。

1.1压缩机模型

压缩机是制冷系统的心脏，其数学模型的优劣关系到空调器模拟的成败。对于装置的稳态仿真而言，从实用化角度出发，可考虑将压缩机与环境的换热环节并入压缩输气环节，由此造成的误差将通过调整压缩机的多边指数，输气系数和电效率来弥补[6]。

1.1.1压缩机出口制冷剂质量流量计算

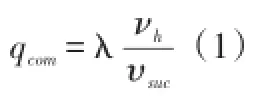
qcom--压缩机出口的制冷剂质量流量（kg/s）；

λ--压缩机输气系数；

νh--压缩机理论排气量（m3/s）；

υsuc--吸气阀处制冷机过热气体的比容（m3/kg）。

式中，D为缸径，S为活塞行程，n为转速；i为汽缸数，对于小型全封闭压缩机，一般取1。

输气系数，λ=λυ∙λp∙λT∙λD

λυ、λp、λT、λD分别为容积系数、压力系数、温度系数、泄漏系数。

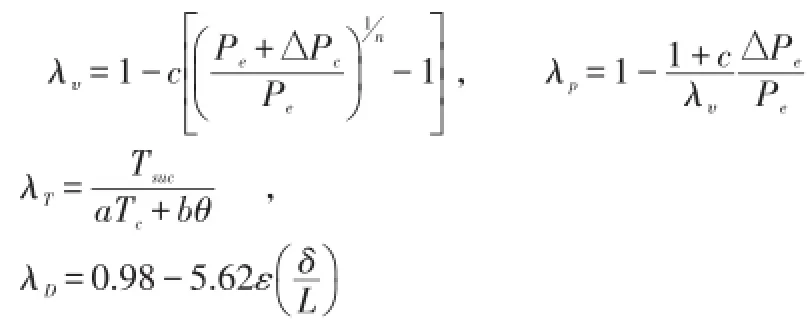
Pc、Pe--分别为冷凝压力、蒸发压力；

ΔPc、ΔPe--分别为排气和吸气压力损失；

n--多变指数；

c--压缩机的相对余隙容积；

θ--过热度；

Tsuc、Tc--分别为吸气温度、冷凝温度；

δ--活塞与气缸之间的径向间隙；

L--活塞环有效密封长度；

ε--压缩比。

1.1.2压缩机的功率计算

理论功率Pth=qcom∙(h2-h1)

式中h2、h1--分别为压缩机出口与进口焓值。

指示效率ηi=λυ+0.0025Te

摩擦功率Pm=Pth∙Vh∙10-3

式中Pm--平均摩擦压力（Pa）。

式中ηmo--平均摩擦压力（Pa）。

1.2冷凝器和蒸发器模型

冷凝器和蒸发器稳态分布参数模型将两者分为不同相区分别建模，即冷凝器分为过热区，两相区和过冷区，蒸发器分为两相区和过热区，由于是稳态模型，因而连续性方程（质量守恒方程）没必要描述，只需对动量守恒方程和能量方程离散化处理，按制冷剂焓值对各个相区分别划分一定数量的微元，迭代算法采用二分法，以换热管总长度的计算值收敛于其真实值为迭代收敛的判据。微元方程如下：

动量方程

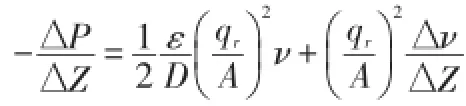
式中：q为质量流量（kg/s）；ε为摩擦系数；ν为制冷剂比容（m3/kg）；∆Z是微元长度（m）；D是换热管内径（m）；A是换热管内截面积（m2）；βf为空气侧换热倍率；P为压力（pa）；Δhj为j点与j－1点比焓值差（J/kg）；α对流换热系数（w/(m2·K)）；T为温度（K）。下标：j为微元序号；r为制冷剂；w为管壁；i为内侧；a为空气；o为外侧。

1.3毛细管模型

制冷剂在毛细管内的流动视为一维绝热流动。由于毛细管直径一般都很细，制冷剂在毛细管中流速相当高，所以在毛细管的仿真数学模型中，有关制冷剂质量、动量和能量方程的所有变量对时间的偏导项都假定为零。流速很高，两相间混合较均匀，故不考虑相间的滑动，采用均相模型。其控制方程如下：

式中：G为质流密度（kg/(m2·s)）；P为压力（pa）；ν为制冷剂比容（m3/kg）；h为比焓值（J/kg）；D是毛细管内径（m）；L是毛细管长度（m）；f为沿程阻力系数（沿程阻力系数采用Churchill关联式）。

1.4充注量计算

充注量的计算关键是选择空泡系数模型，现有的研究结果表明，Premoli模型准确度较好，这是一个经验修正模型，它是通过滑动比的计算进行的，滑动比的计算过程详见文献[6]。

2　系统仿真在产品设计中的应用

2.1仿真样机介绍

以实验方式进行产品设计无疑延长了产品的研发周期，浪费人力，财力。通过系统仿真则可以避免实验的弊端，提高工作效率，并对系统性能指标进行预测分析，为产品性能评价、部件合理匹配提供有价值的参考依据。

本文用系统仿真对样机的毛细管长度、充注量、制冷量以及压缩机耗功率进行了预测，并与参考文献[7]提供的实验数据进行了比较，取得了较好的效果，误差基本控制在±5%左右。样机结构参数如下：

（1）蒸发器

管型：紫铜光管 管根数：26根 高向 管排数：9排 高向管间距：25mm风向管间距：21mm管外径：9.525mm管壁厚：0.35mm单根管长：640mm肋片数：326片型：波纹铝肋片 片间距：1.96mm风向管排数：3片厚：0.12mm分夜路数：1

（2）冷凝器

管型：紫铜光管 管根数：24根 高向管排数：12排 高向管间距：25mm风向管间距：21mm管外径：9.525mm管壁厚：0.35mm单根管长：670mm肋片数：326片型：波纹铝肋片 片间距：1.96mm风向管排数：2片厚：0.12mm分夜路数：1

（3）毛细管

内径：1.37mm实际长度：0.600m

（4）系统标准充注量：520g

（5）仿真计算采用的环境参数如下：

冷凝器测空气参数：干球温度：35℃风量：1026m3/h

冷凝器测空气参数：干球温度：35℃ 湿球温度：19.5℃ 风量：400m3/h

2.2实验数据与仿真结果的比较

见图1。

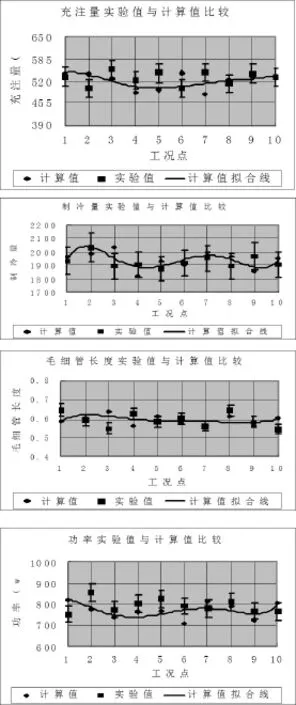
图1　实验值与计算值比较

3　结论及误差分析

（1）采用本文的系统仿真模型可以基本准确的计算制冷剂的充注量、毛细管长度、制冷量以及功率值。

（2）本文是在已知过热度和过冷度的情况下求算上述未知量的，充注量对系统性能的影响也较大，合理的过冷度表征着冷凝器面积在不同相态区上分配关系与整个系统的要求相适应。过冷度太小时，虽然冷凝器两相换热面积大、冷凝器换热能力强，但蒸发器入口处制冷剂干度增大、制冷能力下降；过冷度太大时，蒸发器入口制冷剂干度小、制冷能力强，但冷凝器两相换热面积减小，冷凝器换热能力下降，导致压缩机耗功率增加。

（3）数学模型是在忽略一些次要因素的情况下建立起来的，所以模型自身也存在一定的误差，导致对结果的计算出现误差。另外，在不同工况下模型的适应性差异较大，所以计算结果波动也较大，但基本波动基本控制在实验结果的±5%左右。

（4）由于实验条件有限，本文实验数据只是对文献[7]中提供的实验数据进行拟合后得到的结果，所以存在一定的误差。

[1]葛云亭.房间空调器系统仿真模型研究[博士学位论文].北京：清华大学热能工程系，1997，4.

[2]葛云亭，彦启森.蒸发器动态参数数学模型的建立与理论计算.制冷学报，1995,(1):9－17

[3]葛云亭，彦启森.冷凝器动态参数数学模型的建立与理论计算.制冷学报，1995,(1):17－26

[4]陈华俊，石文星.变频压缩机图形法模型研究.制冷学报，2001,(2):17－22

[5]Huajun CHEN,Wenxing SHI,Shuangquan SHAO.Study on Compressor Model for Simulation of Inerter Air Conditioner by Graph⁃ic Method.Proceedings of the 3rdinternational Compressor Technique onference(ICT2001).Wuxi,china:August 15-18,2001,110-116

张抗（1984－）,男,安徽和县人,合肥工业大学硕士生。