航空发动机立柱式柔性装配工装定位误差分析

李松林，刘思佳，石　宏

(沈阳航空航天大学 航空宇航工程学部(院),沈阳 110136)



航空发动机立柱式柔性装配工装定位误差分析

李松林，刘思佳，石宏

(沈阳航空航天大学 航空宇航工程学部(院),沈阳 110136)

摘要：为提高航空发动机转子类部件在数字化装配过程中的定位精度，采用具有3个平动自由度立柱式三坐标定位单元对航空发动机转子类部件进行数字化装配。对引起数字化装配工装定位误差因素进行综合分析，建立单元定位误差模型，在已建立的误差模型基础上利用MATLAB软件进行计算与仿真分析。结果表明，利用此方法可以找到航空发动机转子柔性装配最佳基准位置，从而提高转子类部件在装配过程中的定位精度。

关键词：航空发动机；立柱式；数字化装配；误差模型；精度分析

航空发动机装配过程是航空制造中的关键环节，同时也是航空制造过程中亟需加强的环节[1]。目前中国在航空发动机装配过程中，很多传统的刚性型架以及用于特定型号大部件的装配工艺已经不再能够胜任航空发动机数字化装配过程中提出的自动化以及柔性化的需求[2-3]。数字化装配技术因采用了柔性定位单元，从而改善了传统装配方式存在的弊端，提高了航空发动机的制造效率和装配质量。由于数字化装配工装的定位精度是影响航空发动机装配质量的重要因素[4]，所以需要设法减小误差源的影响，从而提高装配过程中的定位精度。 目前国外在航空制造过程中的数字化装配系统主要有柔性机翼壁板装配系统、机器人柔性装配系统、柔性翼梁装配系统以及机身柔性装配系统等[5]。空客系列A320、A380等便采用了柔性机翼壁板装配系统对机翼壁板进行数字化装配。国内专家在这方面也进行了大量研究工作，主要研究的是飞机大部件的柔性对接以及总装配[6-7]，而对装配过程中的柔性定位技术研究的比较少。 本文所设计的航空发动机转子柔性装配系统采用立柱式三坐标定位单元[8-9]其定位精度高，运行平稳、可靠。并且可以与自动制动技术、数字化检测技术等结合配置，调整相关配置和参数后，还可适用于不同机型、不同形状尺寸的转子类部件的自动化装配，突出了装配柔性化的优点。最后采用解析法对三坐标定位单元进行了综合误差分析，并建立了定位误差模型。通过对误差源的定量分析，然后对误差进行标定及补偿，进而提高航空发动机在柔性化装配过程中的精度[10]。利用MATLAB仿真分析表明，此定位单元可以提高航空发动机在装配过程中的定位精度。

1　柔性工装构型介绍

为了突出装配工装柔性定位的特点，本文采用模块化立柱式结构进行航空发动机转子的柔性化装配。如图1所示，整个装配工装可以分为三层，并且可以沿着X、Y、Z3个方向进行轴向进给运动，进给轴由伺服电机进行驱动，传动系统主要由导轨与滚珠丝杠组成。工作时，伺服电机驱动滚珠丝杠轴向运动，带动定位执行末端在导轨上移动到空间确定的位置，从而实现装配过程中航空发动机轴的精确定位。

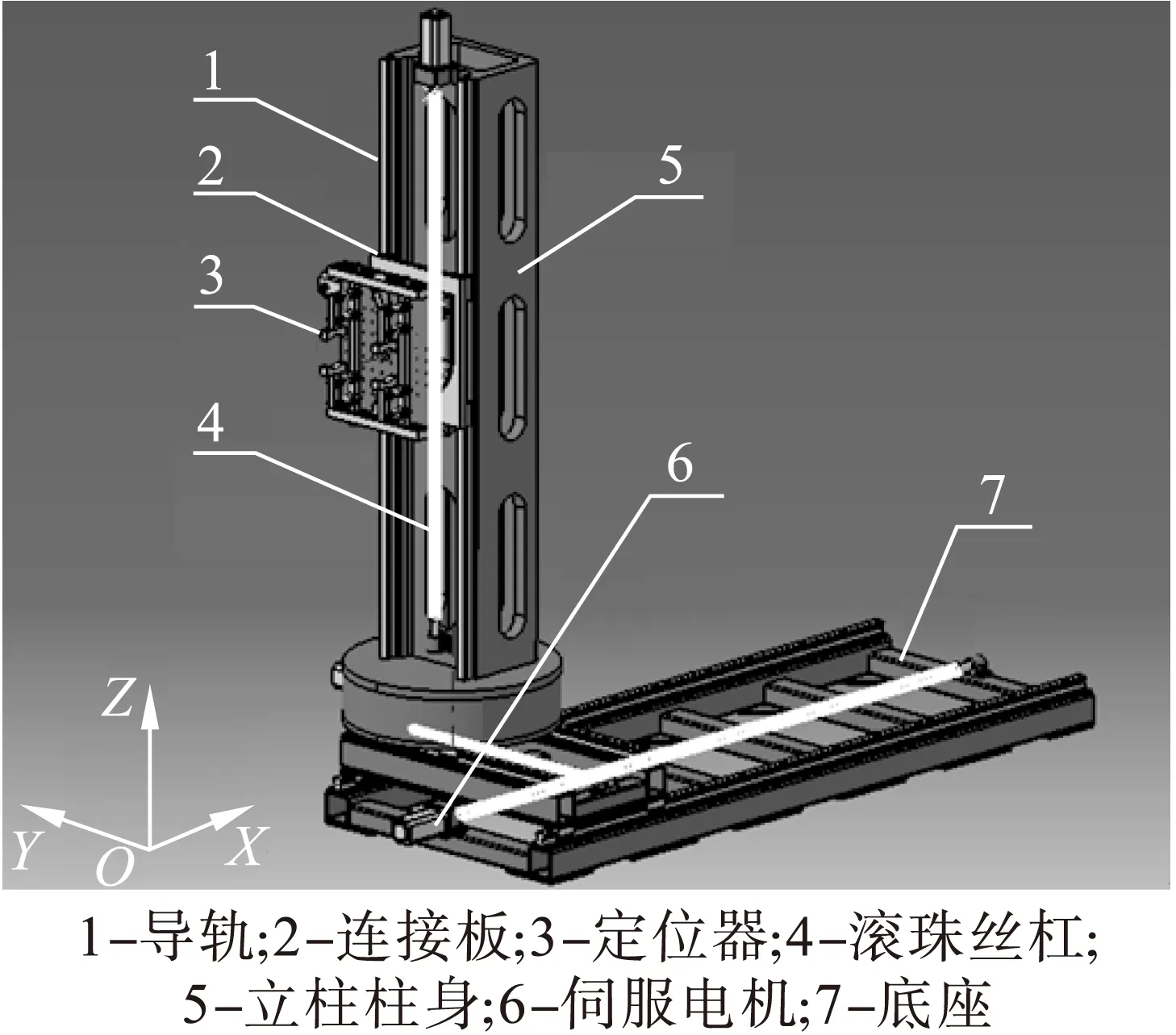
图1　柔性装配工装结构简图

模块化的柱式结构是由竖向运动机构、纵向运动机构、横向运动机构、底座机构以及外形定位器机构五大机构组成[11]。其中构成横向运动驱动系统和导轨导向系统的包括导轨、丝杠、伺服电机、光栅尺、浮动轴承座、联轴器、法兰、底座连接板和连接紧固件等[12]。纵向运动机构和竖向运动机构的传动原理方式与此相同。图2为定位单元传动原理图，3个轴方向上的伺服电机均带有抱闸制动，控制方式可以选择独立控制或者联动控制，并且在运动方向上均设有限位开关、封闭式光栅尺，整个系统采用全闭环控制的方式，从而使得整个伺服系统的安全性和精度得到了保障。

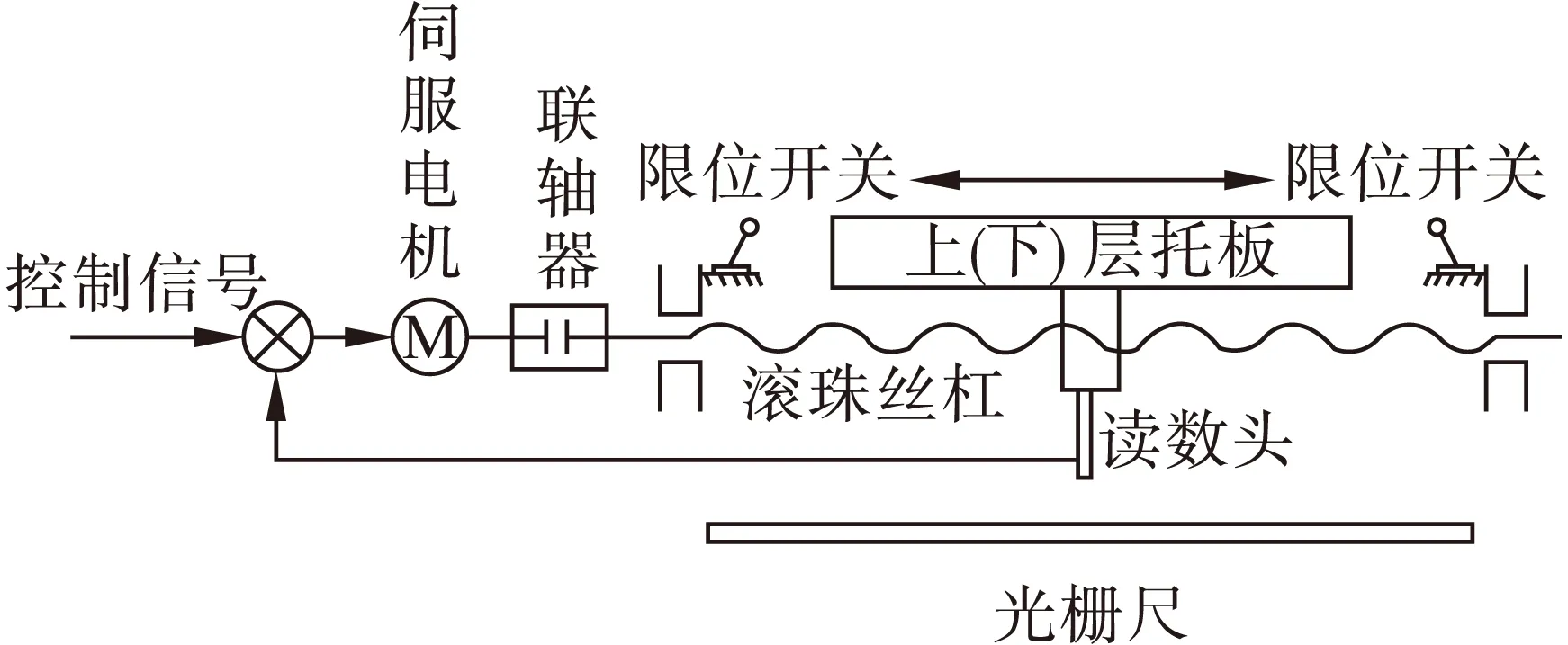
图2　定位单元X(Y/Z)方向传动原理图

2　定位误差分析

定位误差是指定位器在伺服电机的带动下从预定的起始位置开始，沿X、Y、Z3个轴线方向进行进给运动后到达空间中任一指定位置后，定位基准点的实际位置与理论位置的差值。在定位单元轴向进给过程中，暂不考虑由外力引起的变形误差，但由于运行、制造、安装、测量与控制过程中的不确定性，都不可避免的会对定位单元的定位误差产生一定影响。在这些因素中，影响定位执行末端定位误差最主要的因素是由定位单元运动部件的几何精度所产生的定位误差[13-14]，包括滚珠丝杠传动系统在3个轴向运动方向上的导程误差以及导轨导向传动系统的安装定向误差。导轨精度和导轨安装方向偏差直接影响轴向定位误差，而导轨安装基准面设计加工的定向精度则决定着安装定向误差的大小[15]。 柔性装配工装定位单元在轴向进给过程中，X、Y、Z3个方向的进给运动均有单独的伺服控制系统控制，为了便于对定位误差进行建模，认为定位器上定位基准点P的定位误差由X、Y、Z轴向进给位移大小和方向误差分别单独作用的结果。在单个轴向运动过程中，定位基准点P的定位误差由传动系统的轴向定位误差、导程误差与安装定向误差综合作用产生，构成各轴线方向上的线位移误差。以X轴向运动为例，定位单元进给运动过程中其定位基准点P所产生的误差模型如图3所示。

为了便于对误差模型进行分析研究，在底座上建立如图3所示3个直角坐标系。其中，D1(O1,X1,Y1,Z1)建立在底座对称中心点处,其坐标轴方向与定位单元轴向运动坐标轴方向完全重合；D2(O2,X2,Y2,Z2)建立在底座上方的连接板对称中心处，其坐标轴方向与固定直角坐标系D1的坐标轴方向一一平行，并且在连接板的轴向进给运动过程中，其坐标轴不会发生转动，始终与D1平行；D3(O2,X3,Y3,Z3)的建立是因为轴向传动系统的进给误差、导程误差与安装定向误差会引起定位基准点P的线位移误差，其坐标原点与D2坐标系原点重合。理想状态下导轨无安装定向误差，坐标系D2与D3是完全重合的，但在实际运动过程中，由于定位单元各运动部件存在几何误差，因此两坐标轴之间存在一定的夹角。

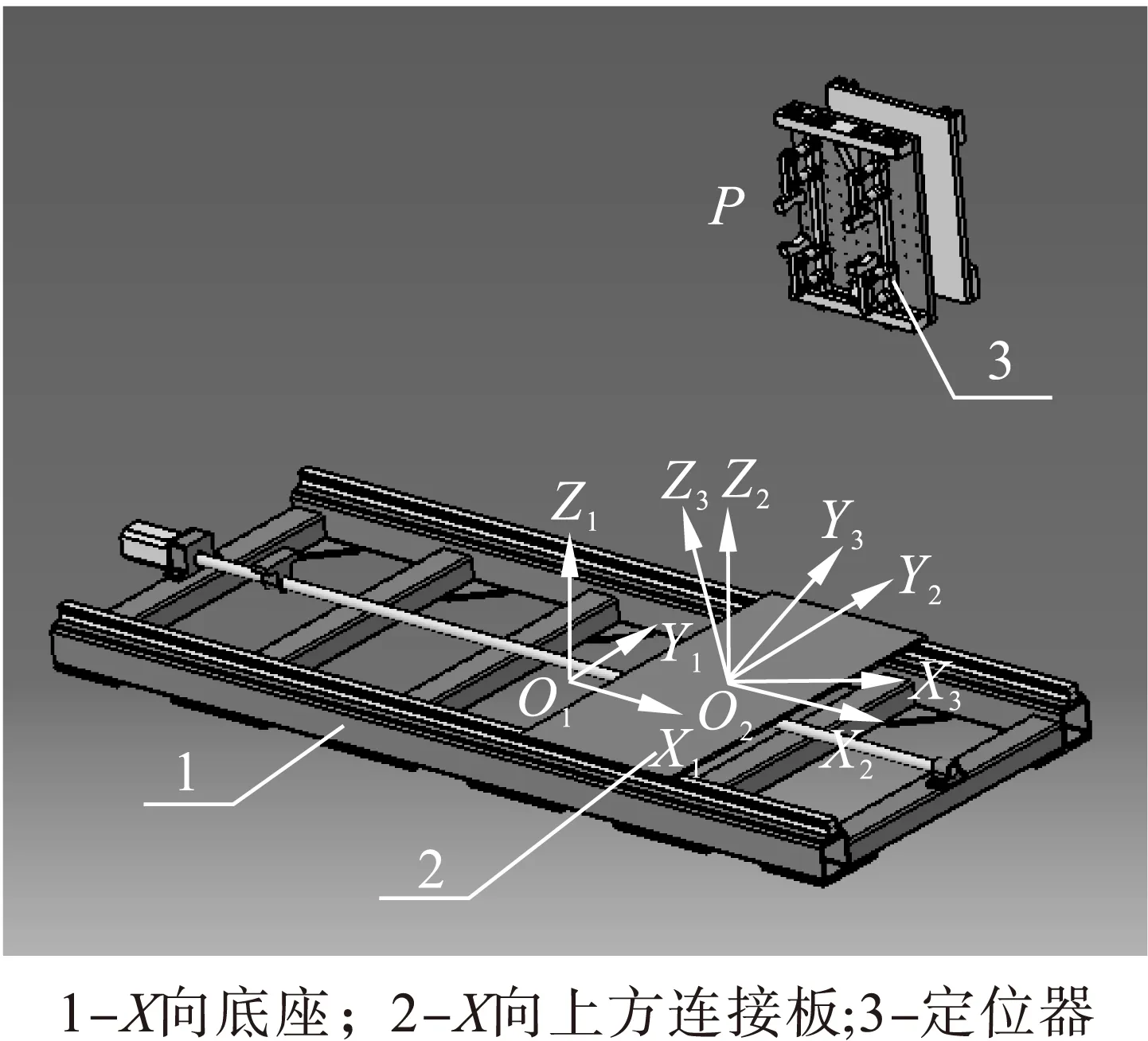
图3　X运动方向定位误差模型

3　误差模型建立

3.1导轨导向传动系统安装定向误差分析

设定定位基准点P的位置矢量OP在D2和D3中的坐标为(x，y，z)，当底座上方的连接板运动到x0处时，如果没有安装定向误差，那么P在D1中的理论坐标为(x+x0，y，z)。但实际运动过程中由于导轨直线度误差、平行度误差与相对基准轴线直线度误差的存在，P点处的位置矢量OP随同坐标系D3沿着Y1、Z1方向平移Δy 、Δz，绕X1、Y1、Z1轴分别转动α、β、γ角度，P点的真实位置就会偏离理论位置，移动至P′处，从而产生定位误差[15]。考虑到导轨导向传动系统的安装定向偏差α、β、γ，则位置矢量OP在坐标系D2中为矢量OP′，设其坐标为(x′,y′,z′)，则

OP′=R(X2,α)·R(Y2,β)·R(Z2,γ)·OP=E1·OP

(1)

式中，R(i,j)表示绕着i轴转动了j角度的旋转矩阵(i=X2、Y2、Z2;j=α,β,γ)；E1是旋转变换矩阵。由于角位移产生的误差非常小，近似令

cosk=1,sink=k(k=α,β,γ)

(2)

αβ=βγ=γα=0

(3)

由式(1)～(3)得

(4)

式中,α、β、γ角的正负号按右手定则来确定，而与绕X3、Y3、Z3轴转动的先后顺序无关。在不考虑坐标系D3平移误差的情况下，当X运动方向上方的连接板运动到x0处时，D3直角坐标系中定位基准点P在D1中的真实坐标是(x′+x0,y′,z′)。定位基准点P由传动系统的安装定向误差转变为定位基准点的线位移误差

(5)

3.2滚珠丝杠运行姿态变化产生的定位误差分析

滚珠丝杠的导程精度即滚珠丝杠轴中心点处的定位精度，通常需要测量丝杠中心点处到定位基准点的距离来计算。假设不考虑光栅尺的反馈测量作用，在传动系统中，因为滚珠丝杠中心位置处在垂直方向上和水平方向都不一样，所以在进给过程中由于运动姿态的改变，定位单元的定位精度也受到一定的影响，其中便包括了滚珠丝杠在水平方向上由于中心位置的不同所产生的左右误差以及在垂直方向上由于中心位置的不同所产生的垂直误差[16]，如图4所示。

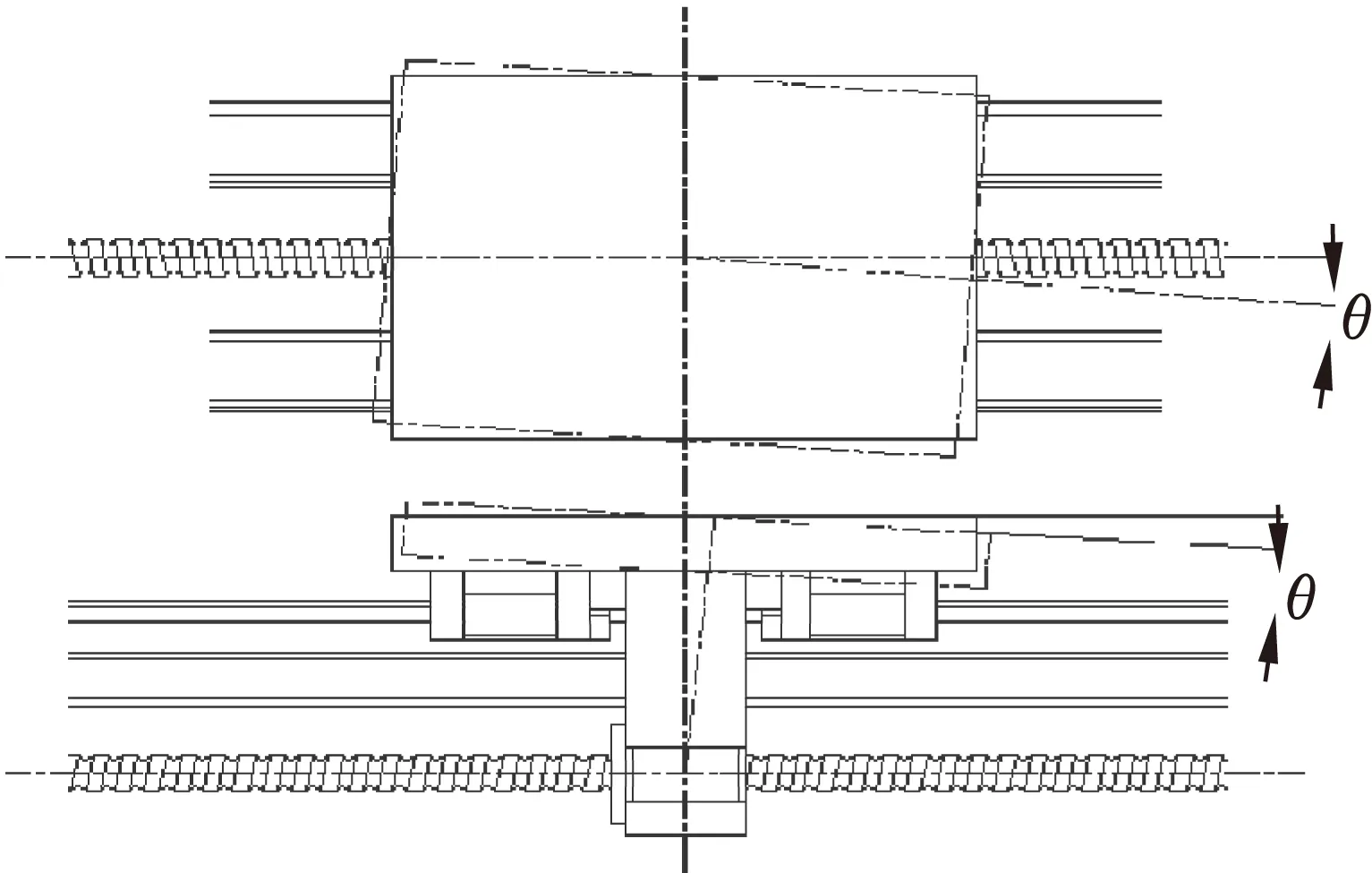
图4　滚珠丝杠运行姿态变化

在坐标系D2中，假设定位基准点P与滚珠丝杠中心的垂直(或水平)距离为L，位置矢量O2P与D2坐标系各坐标轴的夹角为α′、β′、γ′，垂直公差(或左右公差)为θ，则由垂直公差(或左右公差)对点P引起的定位误差W为

W=L·sinθ

(6)

将W进行分解，分别得到由垂直误差对定位基准点P产生的定位误差为

(7)

而由左右误差对定位基准点P产生的定位误差为

(8)

结合(7)式和(8)式，可得到滚珠丝杠的导程精度在运行过程中产生的姿态变化对基准点P的定位误差为

(9)

3.3滚珠丝杠轴向进给误差的定位误差分析

因为滚珠丝杠传动系统在运行过程中存在轴向进给误差Δxt，当给定柔性工装立柱定位单元控制系统中X运动方向的进给值x0，综合考虑所有导向误差以及进给系统的线位移误差与运行姿态变化，固连于定位单元上定位执行末端P点(x，y，z)的线位移误差为

(10)

同理，给定控制系统Y、Z轴向运动方向上的进给值y0、z0时，按照式(1)-式(10)的方法进行推导，同样也可以得出定位基准点P的线位移误差ΔYP和ΔZP分别是

(11)

(12)

3.4空间定位误差模型

根据之前的假设，X、Y、Z轴向进给方向上的位移大小和方向误差对定位基准点P所产生的误差都是单独作用且互不干扰的，可知定位执行末端上定位基准点P的空间总定位误差为各单轴运动方向上对定位基准点P产生的线位移误差之和。在综合误差计算中，考虑到极值情况，由式(1)-(12)按绝对值相加，可得定位基准点P在各运动方向上的误差结果为

[ΔX,ΔY,ΔZ]T=ΔXP+ΔYP+ΔZP

(13)

为了便于利用MATLAB软件对该定位单元误差模型进行分析与仿真，采用位置误差二范数来表示总的空间定位误差，即定位器的真实空间位置与理论空间位置的偏差二范数为

(14)

4　仿真结果与分析

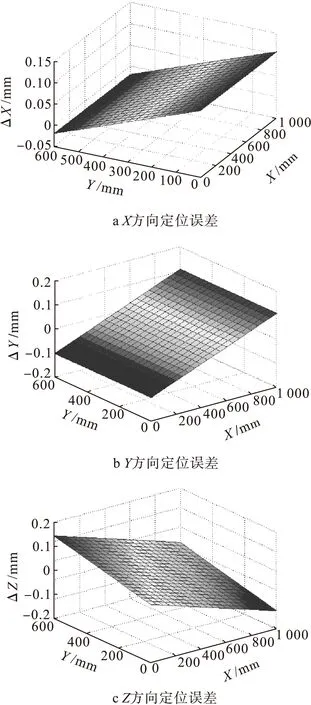
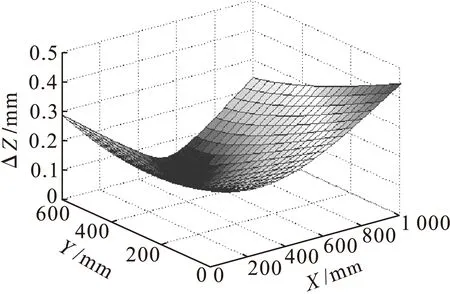
根据建立的定位误差模型，当给定柔性工装的几何参数、初始位置参数和误差参数时，便可以对定位误差进行仿真分析。依照柔性工装的实际尺寸，令定位器的执行末端位姿在z=500 mm，0 mm

表1　定位单元结构参数

根据定位单元单轴定位误差模型公式(10)～(12)在MATLAB软件上进行编程，然后将表1和表2的数据代入程序进行仿真计算，得到X、Y、Z3个方向的定位误差仿真结果如图5所示。由于工装整体属于沿3个方向独立运动的串联式结构，所以定位误差与运动方向理论上是线性关系，由图5可以看出仿真结果与此完全相符。分析图5(a)-(c)可以看出，沿X、Y、Z轴向运动方向定位误差绝对值的变化趋势是一致的，都是随着X、Y轴正向先减少后增大，同时误差浮动变化范围比较小。

表2　定位单元各方向结构参数误差及初始位姿　mm

图5　单轴定位误差

采用同样的方法对空间定位误差模型公式(14)在MATLAB软件上进行编程分析，得到的分析结果如图6所示。由图6可以看出，总的空间定位误差变化与上述结论也是相符合的，并且在接近X、Y轴500 mm处的定位误差变化较小，因此可以把这个位置作为航空发动机转子柔性装配的基准位置。

图6　空间定位误差

5　结论

本文结合航空发动机柔性化装配现状，设计了一种立柱式三坐标定位单元作为发动机转子部件的柔性装配工装，可以实现发动机盘以及转子的精确定位。对各误差源进行分析，并建立空间定位误差模型，应用MATLAB软件对误差模型进行实例仿真，得出了各个运动方向和总空间定位误差以及各误差源对定位精度的影响程度。未来工作中，将开展多轴协同运动精度的控制算法研究、设计集成数字化管理系统，将数字化测量系统与工装运动控制系统集成到同一个控制平台。本研究对航空发动机制造过程中的柔性化装配环节以及改善发动机的装配效率和精度具有重要意义。

参考文献(References)：

[1]石宏,陈英涛.航空发动机数字化装配技术浅析[C].第三届民用飞机先进制造技术及装备论坛，深圳：2011.

[2]邹冀华,刘志存,范玉青.大型飞机部件数字化对接装配技术研究[J].计算机集成制造系统,2007,13(7):1367-1373.

[3]CORBETT J,NAING S.Feature based design for jigless assembly[D].Bedfordshire,UK:Cranfield University,2004.

[4]肖庆东.飞机数字化装配定位技术研究[D].西安:西北工业大学,2007.

[5]范玉清.现代飞机制造技术.北京：北京航空航天大学出版社,2001.

[6]郭洪杰.大型飞机柔性装配技术[J].航空制造技术,2010(18):52-54.

[7]潘志毅,黄翔.飞机制造大型工装布局设计方法研究与实现[J].航空学报,2008,23(3):757-762.

[8]盖宇春,朱伟东,柯映林.三坐标定位器部件刚度配置方法[J].浙江大学学学报,2014,48(8):1434-1441.

[9]李晨,方强,李江雄.基于三坐标定位器的大部件调姿机构误差分析.机电工程,2010,27(3):6-12.

[10]朱宁,李伟楠,石宏,等.航空发动机柔性装配工装定位精度分析与研究[J].沈阳航空航天大学学报,2013,30(2):4-8.

[11]张远远,王仲奇.一种三坐标的双支臂定位器:中国,201210199030[P].2012-10-03.

[12]张远远,王仲奇,康永刚.基于多点技术的柔性支撑定位方法研究[J].机械设计与制造工程,2013,42(5):7-11.

[13]RICHEY M C.System and method for producing an assembly by directly implementing three-dimensional computer-aided design component definitions:USA,6922599B2[P].2005-07-26.

[14]周红力.数控机床定位精度研究[D].长沙:湖南大学,2008.

[15]郭志敏,蒋军霞,柯映林.一种精密三坐标POGO柱设计与精度研究[J].浙江大学学报,2009,43(9):1649-1654.

[16]郭飞燕,王仲奇,康永刚,等.飞机立柱式柔性工装定位误差分析与精度保障[J].计算机集成制造系统,2013,19(8):2036-2042.

(责任编辑：宋丽萍英文审校：王云雁)

收稿日期：2015-09-12

作者简介：李松林(1989-)，男，山东烟台人，硕士研究生，主要研究方向：航空发动机强度、振动及噪声，E-mail：lisonglin1225@163.com；石宏(1961-)，女，辽宁沈阳人，教授，主要研究方向：航空发动机制造与维修，E-mail：shihong0809@163.com。

文章编号：2095-1248(2016)02-0022-05

中图分类号：TN911.4

文献标志码：A

doi:10.3969/j.issn.2095-1248.2016.02.005

Error analysis of column flexible assembly tooling positioning of aero-engine

LI Song-lin，LIU Si-jia，SHI Hong

(Faculty of Aerospace Engineering，Shenyang Aerospace University，Shenyang 110136,China)

Abstract：A method of posture alignment based on a three-axis column locating unit was developed to improve the positioning accuracy in aero-engine digital assembly system.The positioning error model of locating unit was constructed through analysis of the factors affecting positioning accuracy.Then the comprehensive positioning error was calculated and the simulation analysis was conducted with MATLAB software.Simulation results show that the best reference position could be found and the accuracy of the locating units could be improved in the assembly process.

Key words：aero-engine;vertical column type;digital assembly;error model;accuracy analyzing