碳/碳复合材料薄壁壳结构在热声载荷作用下非线性响应
2016-08-15李华山沙云东唐晓宁赵奉同栾孝驰蒋金卓
李华山,沙云东,唐晓宁,赵奉同,栾孝驰,蒋金卓
(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136)
碳/碳复合材料薄壁壳结构在热声载荷作用下非线性响应
李华山,沙云东,唐晓宁,赵奉同,栾孝驰,蒋金卓
(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136)
摘要:复合材料壳结构在热声载荷下呈现复杂的振动响应。以四边简支复合材料壳结构为研究对象,采用有限元法计算了复合材料壳结构在不同温度和声压级组合下的振动响应。结合应力的时间历程、概率密度、功率谱密度进行研究。结果表明:屈曲前,应力概率密度基本服从正态分布;屈曲后,应力概率密度不服从正态分布,随着温度继续升高应力的概率密度变窄变尖,但是概率密度分布近似正态分布。热载荷产生的热应力会增加复合材料薄壁壳结构的刚度,改变壳结构基频,声载荷的增加会使复合材料薄壁壳结构的响应增大。
关键词:复合材料;壳结构;热声载荷;非线性响应
先进高速飞行器的热防护系统将由碳/碳复合材料构成[1],而航空发动机为了减轻结构重量,广泛采用薄壁结构。伴随新技术的发展,现代航空航天器的表面薄壁结构承受着高水平随机压力载荷的作用,由于复合材料具有强度质量比高的优点,正在逐步应用于航空发动机以及航空航天器[2-3]。随机压力载荷可能来源于发动机喷气噪声,也可能来源于边界层压力脉动。除了随机压力载荷,高速飞行器薄壁结构一般还处于气动加热引起的高温热载荷作用下[4]。由于发动机喷气的加热作用,直升飞机和垂直起降、短距降落飞机等低速飞行器的表面蒙皮同样处于严酷的热声载荷作用下[5-8]。本文进行复合材料薄壁结构在热声载荷作用下的响应计算,分析热载荷和声载荷对结构非线性响应的影响规律[9-11]。 C.Mei首先将FEM拓展到热-声载荷作用下的各向同性梁和板结构,假设热载荷为稳态温度分布,声载荷为零均值高斯白噪声[12],利用迭代法求解结构热屈曲控制方程,得到结构的热屈曲挠度和热应力,然后将热屈曲挠度和热应力作为随机声激励下振动响应分析的初始条件,使用热屈曲结构的线性模态振型以降低运动方程组的阶次[13],得到较低阶的非线性模态方程组,进行线性化处理后再次进行模态转换得到方程的解。Dhainaut和Mei研究了各向同性薄板由于非白噪声激励引起的非线性随机响应,结果显示带有非白噪声功率谱密度比相应的等价白噪声在实际飞行数据产生更高的应力特性并降低疲劳寿命[14]。本文以四边简支复合材料壳结构为研究对象,采用有限元法计算了在不同温度和声压级组合下的振动响应。
1 复合材料薄壁壳结构的控制方程和统计理论
复合材料薄壁壳结构应变[15-16]

(1)
(2)
式中,w为横向位移,[K]是线性刚度矩阵,[KT]热刚度矩阵,[Kr]是恢复力刚度矩阵,[N1]是一阶非线性刚度矩阵,[N2]是二阶非线性刚度矩阵,K是剪切修正系数,{PT}是热载荷,{Pr}是恢复力。利用迭代法求解热屈曲问题,公式(2)简化为
{w}={PT}-{Pr}
(3)
引入函数{Ψ(W)}到方程(3),公式(3)展开为
{Ψ(W)}=
{w}-{PT}+{Pr}=0
(4)
{Ψ(W)+δW)}={Ψ(W)}+
(5)
(6)
定义概率密度函数p(x)为
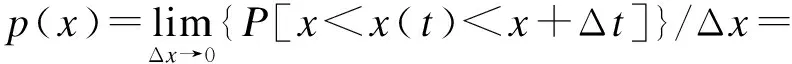
(7)
描述随机信号某一时间t的瞬时值和另一时刻t+τ瞬时值的依从关系的自相关函数Rx(τ)为
(8)
自相关函数Rx(τ)在时间上给出了平稳过程的基本统计特性,它的傅里叶变换记为
(9)
Sx(ω)是从频率域上描述平稳过程基本统计特性的函数,称为平稳随机过程{x(t)}的功率谱密度,简称谱密度。
2 算例及分析
本文选取碳/碳复合材料薄壁壳作为研究对象。薄壳几何尺数如图1所示,a·b·h=0.3 m×0.3 m×0.005 m,半径R=1.5 m,边界条件为四边简支。材料属性如表1所示,铺层数5,每层厚度0.001 m,铺角-45°/45°/-45°/45°/-45°。

图1 壳结构几何尺寸示意图

表1 复合材料(C/C)薄壁壳的材料参数
2.1噪声载荷
本文的声载荷为有限带宽高斯白噪声。高斯白噪声载荷的功率谱密度在带宽范围内是一条直线,概率密度服从正态分布。噪声载荷的功率谱密度(PSD)可用下面公式表示
式中,SPL为声压级,Δf表示频率带宽,截止频率1 500 Hz。图2为165 dB噪声载荷的时间历程,功率谱密度和概率密度。

图2 声载荷时间历程、功率谱密度、概率密度图
计算四边简支复合材料壳结构的模态频率与临界屈曲温度如表2、表3所示。

表2 复合材料壳结构模态频率

表3 复合材料壳结构临界屈曲温度
2.2响应计算与分析
应力的概率密度是应力的统计规律,计算复合材料壳结构的概率密度来分析应力响应的特性。声载荷的概率密度完全服从正态分布,那么线性材料的壳结构响应的概率密度也应该服从正态分布。从图4(a)中可以看出,在温度为零时,复合材料薄壁壳结构应力响应的概率密度基本服从正态分布。而图4(b)、图4(c)表明由于温度的影响,复合材料壳结构应力响应概率密度不服从正态分布。在屈曲后,复合材料壳结构中点x向应力时间历程处于压缩状态,如图4(d)-图4(f)所示,x向应力值为负值。同时,对比屈曲前后应力概率密度分布,可以发现,由于热屈曲的产生,应力概率密度不服从正态分布,从应力概率密度图中可以清晰看到屈曲后的应力幅值变化范围明显小与屈曲前的应力幅值的变化范围。结果表明温度对响应的影响,随着温度的逐渐升高,复合材料壳结构的应力均值绝对值增大,而应力幅值增加,概率密度逐渐不符合正态分布。
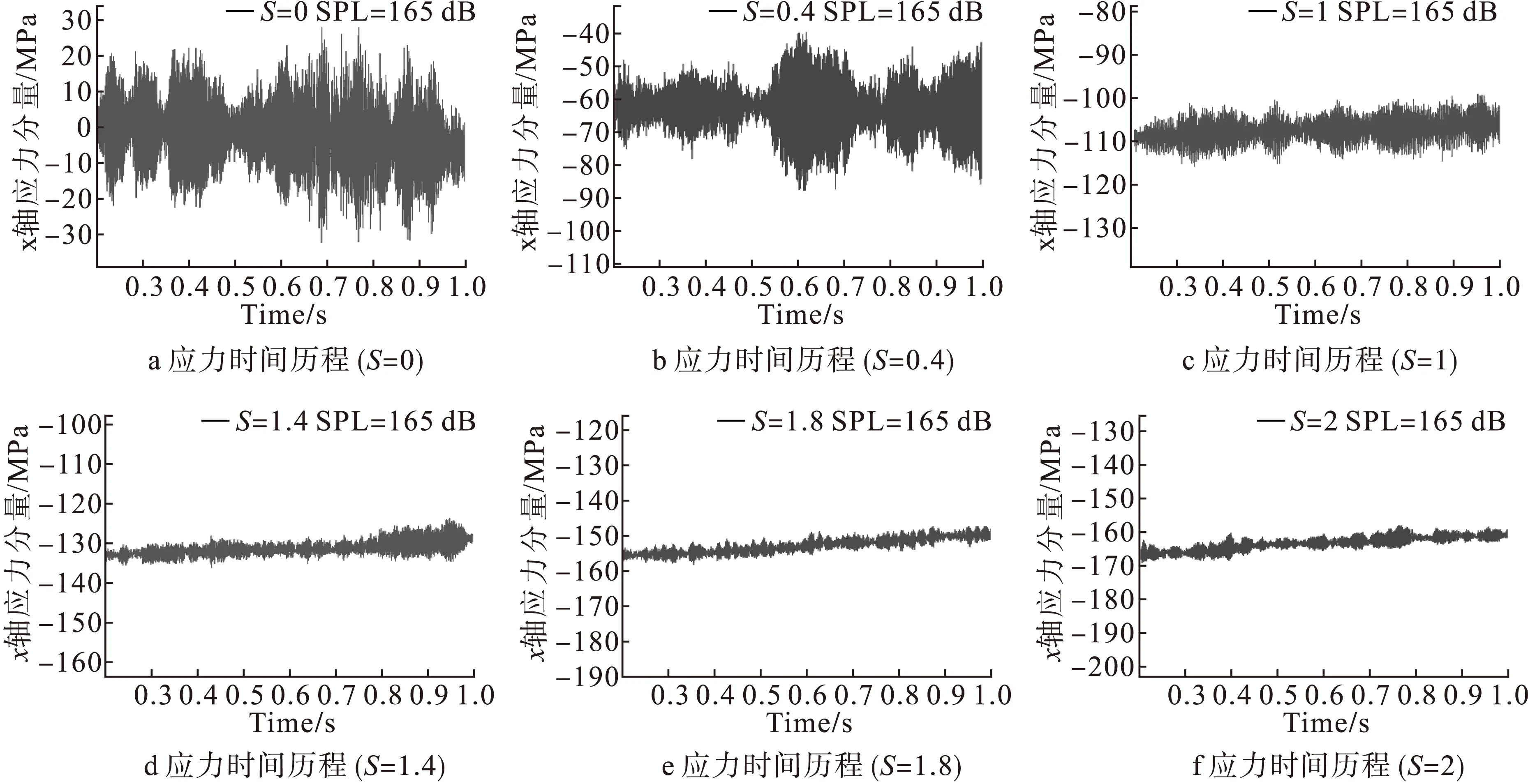
图3 简支壳中点x向应力响应时间历程(SPL=165 dB)
应力功率谱是应力的自相关函数的傅立叶变换,通过频域分析可以得到固有频率的变化情况。声压级为165 dB,S=0,0.4,1,1.4,1.8,2。考虑基频变化情况,定常声压级下,屈曲前如图5(a)所示,温度从S=0上升到S=1,复合材料薄壁壳结构基频从S=0时的633 Hz上升至S=1时的1 160 Hz;屈曲后,温度升高,导致复合材料壳结构基频由S=1.4时的1 300 Hz上升至S=2时的1 460 Hz。这是由于温度的增加致使薄板逐渐硬化,导致复合材料壳结构的刚度增加,从而使其基频升高。结果表明温度会是复合材料壳结构的刚度产生变化,会影响响应的特性。
由图6可知,在相同声压级165 dB下,随着温度升高,应力响应幅值和均值的绝对值都会增加。在S=3以上的时候复合材料壳结构的应力响应出现新的特性,相较与S=1.4,1.8,2发现应力响应在0.3s~0.4s之间会突然出现突变,从围绕屈曲后的一个平衡位置的随机振动跳变到围绕另一个屈曲后平衡位置的随机振动,两个平衡位置十分接近。如图7(a)所示应力的概率密度不服从正态分布,呈现单峰值状态。图6(b),图6(c)中所示应力的概率密度变窄变尖,但是应力的概率分布近似正态分布。

图5 简支壳中点x向应力功率谱密度密度(SPL=165 dB)

图6 简支壳中点x向应力响应时间历程(SPL=165 dB)

图7 简支壳中点x向应力响应概率密度(SPL=165 dB)
3 结论
本文利用有限元数值计算方法对复合材料壳结构进行热声激振计算,得到结论如下:
(1)在热屈曲前,随着温度的递增,复合材料壳结构响应均值绝对值增大,响应幅值增加,屈曲后较屈曲前应力均值绝对值增大,应力响应的幅值增加,应力浮动范围变窄。屈曲前,应力概率密度基本服从正态分布;屈曲后,应力概率密度不服从正态分布,出现单峰值状态,随着温度继续升高应力的概率密度变窄变尖,但是概率密度分布近似正态分布。
(2)温度会对复合材料壳结构的响应特性产生影响,在相同声压级下,温度增加产生的热应力会使复合材料壳结构逐渐硬化,导致复合材料壳结构的刚度增加,从而使其基频升高。
(3)壳结构在热声载荷作用下温度为零时应力响应围绕平衡位置进行随机振动,当温度略微增加时应力响应就会出现围绕屈曲后某个位置进行随机振动,壳结构处于压缩状态。当温度继续增大,应力响应在0.3s~0.4s之间会突然出现突变,从围绕屈曲后的一个平衡位置的随机振动跳变到围绕另一个屈曲后平衡位置的随机振动,两个平衡位置十分接近。
参考文献(References):
[1]CHEN L M.Mechanical analysis for composite materials,china science and technolog press.ISBN978-7-5046-4387-2/V 2008:188-190.
[2]RADU A G,YANG B,KIM K,et a1.Prediction of the dynamic response and fatigue life of paIlels subjected tothermo-acoustic loading[C].45th AIAA/ASME Structure,Structural DynaInics & Materials Conference,2004.
[3]DHAINAUT J M,X G,C M,et al.Nonlinear random response of panels in an elevated thermal-acoustic environment[J].Journal of Aircraft,2003,40(4):683-691.
[4]范绪箕.高速飞行器热结构分析与应用[M].北京:国防工业出版社,2009.
[5]MEI.C.Nonlinear random response of composite panels in an elevated thermal environment[R].Old Dominion University,Norfolk,VA,2000.
[6]ADAM J CULLER,JACK J MCNAMARA.Impact of fluid-thermal-structural coupling on response prediction of hypersonic skin panels[J].AIAA Journal,2011,49(11):59-65.
[7]JEAN-MICHEL DHAINAUT,XINYUN GUO,CHUH MEI,et al.Nonlinear random response of panels in an elevated thermal-acoustic environment[J].Journal of Aircraft,Vol.40,No.4,July-August 2003,40(4):85-94.
[8]A MATNEY,R A PEREZ,S M SPOTTSWOOD,et al.Nonlinear structural reduced order modeling methods for hypersonic structures.53rd AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics and Materials Conference,20th AI 23-26 April 2012,Honolulu,Hawaii.AIAA 2012-1972.
[9]鲍东东,沙云东,魏静.热声载荷作用下复合材料薄板的非线性响应[J].沈阳航空航天大学学报,2013,30(5):5-9.
[10]金奕山,李琳.随机振动载荷作用下结构Von Mises应力过程的研究[J].应用力学学报,2004,21(3):13-16.
[11]SHA Y D,LI J Y AND GAO Z J.Dynamic response of pre/post buckled thin-walled structure under thermo-acoustic loading[J].Applied Mechanics and Materials,2001(80):536-541.
[12]ADAM J.CULLER,JACK J.MCNAMARA.Coupled flow-thermal-structural analysis for response prediction of hypersonic vehicle skin panels[C].51st AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference,2010,Orlando,Florida.
[13]沙云东,朱林,栾孝驰,等.带有温度梯度的热载荷与声载荷作用下薄板动态响应[J].振动与冲击,2014,33(18):102-109.
[14]DHAINAUT J M,GUO X,MEI C,et al.Nonlinear random response of panels in an elevated thermal-acoustic environment[J].Journal of Aircraft,2003,40(4):683-691.
[15]徐芝纶.弹性力学[M].北京:高等教育出版社,2006.
[16]孙训方.材料力学[M].北京:高等教育出版社,2002.
(责任编辑:宋丽萍英文审校:王云雁)
收稿日期:2015-09-23
基金项目:航空科学基金(项目编号:02C54007)
作者简介:李华山(1990-),男,辽宁庄河人,硕士研究生,主要研究方向:航空发动机强度、振动及噪声,E-mail:1157665203@qq.com;沙云东(1966-),男,黑龙江阿城人,教授,主要研究方向:航空发动机强度、振动及噪声,E-mail:Ydsha2003@vip.sina.om。
文章编号:2095-1248(2016)02-0006-06
中图分类号:V232.6
文献标志码:A
doi:10.3969/j.issn.2095-1248.2016.02.002
Nonlinear response of carbon/carbon composite shell structure subject to thermo-acoustic loadings
LI Hua-shan,SHA Yun-dong,TANG Xiao-ning,ZHANG Feng-tong,LUAN Xiao-chi,JIANG Jin-zhou
(Liaoning Province Key Laboratory of Advanced Measurement and Test Technology of Aviation Propulsion Systems,Shenyang Aerospace University,Shenyang 110136,China)
Abstract:Composite shell structure presents complex vibration response under thermal acoustic loads.To calculate vibration response of simply supported composite shell structure under the different temperature and sound pressure levels,the finite element method is used.Combining with the time history of stress,vibration response of the probability density and power spectral density,the characteristic of vibration response is analyzed.The results show that stress probability density is in normal distribution before buckling but after buckling it is not in normal distribution.As temperature rises continually,stress probability density narrows and sharpens in approximate normal distribution.The thermal stress caused by thermal load increases the stiffness of composite shell structure,which changes the fundamental frequency of shell structure.The acoustic load rise leads to more response of the shell structure.
Key words:composite material;shell structure;thermal and acoustic loads;nonlinear response
