求解非线性约束优化问题的精确罚函数方法

谭　俊，陈建玲，苏江波

（1.运城学院　应用数学系；2.运城学院　物理与电子工程系，山西　运城　044000）

·国家自然科学基金项目

求解非线性约束优化问题的精确罚函数方法

谭俊1，陈建玲2，苏江波2

（1.运城学院应用数学系；2.运城学院物理与电子工程系，山西运城044000）

非线性约束优化问题属于一般形式的非线性规划问题范畴，它也是数学优化研究中的关键难点.用非约束优化问题来求解约束最优化问题的主要方法有两种：拉格朗日乘子函数法与罚函数法，本文将主要论述的就是求解非线性规划中的精确罚函数法，通过这种算法的相关理论与实践算例来求证它的有效性.

精确罚函数；非线性约束优化；规划；算例

罚函数法就是通过求解一个或多个罚问题来约束规划目标问题的解，一般来说所得到罚问题的解就是初始问题的最优解.如果罚参数达到一定指标时，单独罚问题的最优解就应该是原约束规划问题的最优解，所以此罚问题中的罚函数就应该被称为精确罚函数.精确罚函数也是求解非线性约束优化问题的有效方法之一，它在一定条件下所呈现的光滑性与精确性都是值得借鉴的.

1　精确罚函数

对于非线性约束优化问题而言，罚函数法是最有效的解决方法之一，但从方法属性层面看，罚函数法的天生病态性质又局限了它能力的发挥，所以人们希望给出一种基于精确角度的新罚函数法，以此来解决传统罚函数法中所固有的天生病态性质.

1.1罚函数法与精确罚函数法

在传统数学函数理论中，罚函数理论属于经典之一，它依靠对罚函数项的添加来实现对无约束优化问题的解决，使罚函数能够在趋于无限大的过程中获取原始规划问题的最优解.相比较而言，精确罚函数理论则通过求解个体无约束优化问题作为最优解，这就暴露了传统罚函数法的函数病态性质缺陷，也就是由于病态罚因子无限制增大或减小所引起的求解不够精确问题.精确罚函数法作为一类新的罚函数算法，可以将精确罚函数的非光滑属性光滑化.不过精确罚函数方法也有一定缺点，例如在实际计算中由于无法得知罚函数的具体数值，所以这就影响了诸如Newton算法的有效性，因此可以见得使用罚函数法的要点就是在于它的可微性、精确性与光滑性.罚函数的选择与计算应该满足某个基本要求，比如迭代过程中对罚函数极小化的操作与应用，它能够为原有非线性约束化问题寻找到一个局部的最优解，并且在适当条件下确保罚函数算法的全局收敛性，使函数估值更加简易化.

1.2精确罚函数的具体构造

作为解决约束优化问题精确罚函数，它解决问题的主要思路就是通过寻找某个容易的求解来替代问题，并满足一定条件，使所找到的解恰好符合原问题的解，这样整各求解问题就会变得相对简易化.因此在构造罚函数前，应该首先明确精确罚函数的构造原理，即对某一个罚参数所对应ρ的无约束优化问题最优解也就是对原问题的最优解.基于上述理论，可以阐述非线性约束优化问题中精确罚函数方法的基本构造结构:

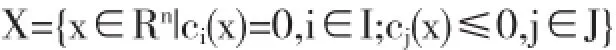
如果:Ø（y）=maxβ（0，y），β∈N，就可以基于Ø（y）推导出y的连续一阶导数.如果y≥0，就有Ø'（y）=βyβ-1，当y＜0时，就有:Ø'（y）=0.基于上述理论推理，对罚函数F（x，u）进行推导:

当F（x，u）≥0时，就可以考虑基于精确罚函数法下所对应的无约束优化问题:

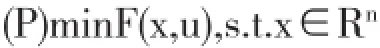
在上式中当设置最优解为xu*时，x，u取任意值，就有0≤F（xu*，u）≤（x，u），而且有F（xu*，u）=0，它的充要条件为:

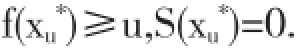
1.3精确罚函数的算法说明

根据精确罚函数的基本性质及原理，并参考P （x，M）函数的连续性就可以得知，如果选择已知函数f*的近似值，就能够通过对问题求解来得到非线性约束问题的最优解.所以在运用精确罚函数方法是可以基于这一思想来推导出该算法的具体流程步骤.

步骤1:首先输入函数f*的下界初值并满足f*≥α0，由此可以取得可行点x0.当有F（x0）=0时，将β0作为f*的上限值，并满足β0=f（x0）.或者在满足f*≤β0时，也可以求得minF（x）的值.

步骤2:当Mk=（1-θ）αk+θβk时，若参数θ的取值范围在0＜θ＜0.5，假设θ=0.3，就可以求解minP

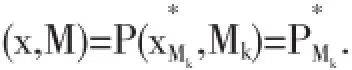
步骤4:重复第二、三步骤就可以得到算式βk+1-αk≤ε，此时问题的最优解就应该为:x*=x*Mk.在上述算法的四个步骤中，f*作为下界不能选择过小，选择过小就很容易产生溢出而导致计算无法成功，因此根据收敛性定理可知，当上述算法中若产生αk，βk时，它们应该满足αk≤f*≤βk，而且由于两参数之差等于0，因此可以得出结论，精确罚函数的算法是应该具备收敛性的.

通常情况下，传统的一般罚函数构造都是按照约束问题所给出的，所得到的罚问题的解也符合原始问题的近似解.而精确罚函数所能实现的就是一般罚函数的精确解，这也是精确罚函数的最重要特性.如上述算法步骤中如果f（x）在一阶具有可微性，那么精确罚函数P（x，M）在一阶也同样具有可微性.同理，f（x）与P（x，M）在二阶也具有可微性，因此可以证明罚函数P（x，M）应该是关于M的减函数，并且在满足相应条件下，精确罚函数的最优解就能够符合原问题规则，成为原问题的最优解，这就是对原问题的一种新形式算法设计，精确罚函数目前已经被广泛应用到计算机编程工作当中，应用相当灵活实用［1］.

2　逼近l1的精确罚函数算法

针对逼近l1的精确罚函数形式是一种全新的近似渐进计算方法，它能够证明罚函数的近似算法所能在序列上得到的聚点数量，并根据聚点来为原问题求得最优解.如果所得序列无界，就要根据实际状况相应的展示序列值的收敛性，直到为最优解创造充分条件［2］.另外，在Fromovitz约束规范下也可以证明一点［3］，即当β越大时，γ的充分值就越小，但是由此所产生的迭代极小点都存在可行性，它们间接为l1精确罚函数在不精确罚函数的情形下进行推广并允许通过简易化算例进行验证.

2.1逼近l1的精确罚函数算法的相关问题及方法解析

在对逼近l1精确罚函数算法进行解析之前，要考虑可微非线性规划问题，例如为ε≥0定义设计松弛可行集合，有:

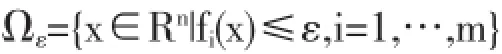
在公式中，当Ω0是精确罚函数的可行集合时，就可以列出以下假设:

当罚函数式中存在ε＞0，Ωε就是有界限的；

而如果罚函数式满足Fromovitz约束规范，就可以得到一个任意的最优解x*，当h∈Rn且ρ＞0时，罚函数式就会满足▽fi（x*）Th＜-ρ.如果对任意数i=1，…，m，设定条件为fi（x）＜0，则点x∈Rn就可以被称之为内点，此时按照Fromovitz约束规范就可以证明内点是一定存在的.以下可以给出逼近l1精确罚函数具有可微性的罚函数形式公式为:

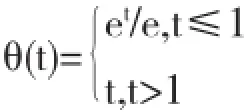
再进一步推算得出一阶导数应该为:

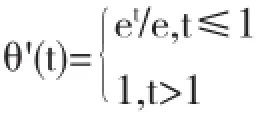
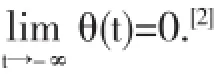
2.2逼近l1的精确罚函数算法的相关算法解析

为了证明逼近l1精确罚函数算法的可行性，本文假设了适应于任意函数的β、γ值，假设其满足: β0≥1，γ∈（0，1］，当fβ、γ（·）中含有极小点时，它的算法步骤如下:

步骤1:设置β0=1，γ0=1，且k=0.

步骤2:根据步骤1带入参数计算可得:

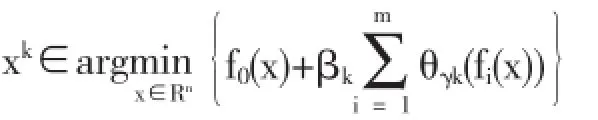
步骤3:γk+1=γk/2，如果xk为可行点，就有βk+1=βk；如果xk为不可行点，就有βk+1=2βk.

步骤4:当k=k+1时，按照步骤2就可求得逼近l1精确罚函数的值.

根据上述4步骤算法就可以得出以下结论，如果存在任意条件如t≤0或t＞1时，θγk（t）的逐点收敛值就应该为t+.而如果当βkγk≤1时，它的可行域内点x~就有:

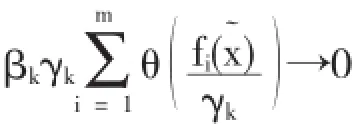
3　基于精确罚函数方法的非线性约束优化问题算例解析

3.1算例1

假设有:minx1+x2，且s.t.x12-x2≤0，-x1≤0

根据上述假设条件可以看出该算例的最优解应该为（x1*，x2*）=｛0，0｝，它的最优目标值应该是0，而其对应的非线性法函数应该被定义为以下:

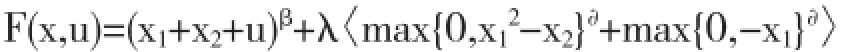
具体到各个参数则分别取值为:∂=5，β=3， λ=100.当u=-1时，非线性约束化问题minx∈XF（x，-1）就可以得出最优解x*的值就应该为（1/3，2/3），它所对应的目标数值就应该为F（x，-1）=0.

3.2算例2

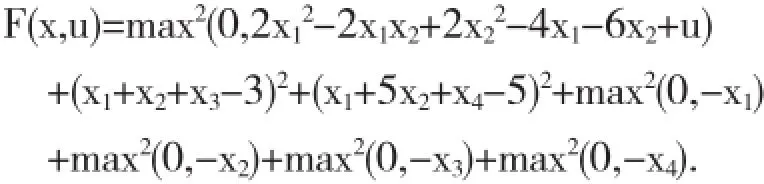
通过上述两个基于精确罚函数方法的非线性约束优化问题的计算就证明了该方法对解决原罚函数问题的有效性［6］.

4　总结

本文通过对精确罚函数的理论阐述与对非线性约束优化问题计算求解得出了诸多结论，例如关于逼近l1精确罚函数若干性质的实现.更重要的是对非线性约束优化问题中原罚函数的精确求解，在保留原有罚函数问题中不可微部分函数值不变的基础上，满足了罚函数式中的可微性与光滑性，进而提升了精确罚函数算法的效率与质量，提升了算法的收敛速度，证明了精确罚函数方法在非线性约束优化问题中求解的有效性与实用性.

〔1〕王桂艳.求解非线性约束优化问题的精确罚函数方法［D］.北京交通大学，2009.5-18.

〔2〕王银河.非线性优化问题的罚函数算法和拟Newton算法［D］.重庆大学，2010.10-22.

〔3〕魏大松.非线性优化问题的精确罚函数算法研究［D］.重庆大学，2007.13-15.

〔4〕程桂香.非线性最优化问题的一族新的罚函数方法研究［D］.首都师范大学，2006.15-34.

〔5〕张春慨，李霄峰，邵惠鹤，等.基于线性搜索的混沌优化及其在非线性约束优化问题中的应用［J］.控制与决策，2001，16（1）：123-125，12.

〔6〕蔡力，朱德通.整体收敛的非线性等式约束优化问题的不精确修正正割方法［J］.上海师范大学学报（自然科学版），2011，40（5）：441-45.

O221.2

A

1673-260X（2016）07-0001-03

2016-04-08

运城学院博士启动基金项目资助（YQ-2012011，YQ-2014013）；国家自然科学基金项目资助（U1431125）