两回路/三回路驾驶仪对闪烁背景下制导精度的影响

王广帅, 林德福

(北京理工大学宇航学院, 北京 100081)



两回路/三回路驾驶仪对闪烁背景下制导精度的影响

王广帅, 林德福

(北京理工大学宇航学院, 北京 100081)

针对闪烁噪声成为雷达末制导段主要随机误差之一,从控制系统设计的角度研究了闪烁背景下制导精度改进问题。建立了闪烁噪声作用下的制导控制模型,模型中引入了平台导引头动力学,研究了闪烁噪声对制导指令的影响;将控制系统设计指标选择为时域/频域混合的设计指标,选用开环穿越频率约束下极点配置方法完成了两回路/三回路过载驾驶仪的设计,研究了不同控制系统设计指标下的比例导引末制导脱靶量。研究表明，比例导引制导系统采用经典两回路过载驾驶仪时,通过适当增大开环穿越频率、适度减小系统阻尼,可以减小闪烁噪声造成的脱靶量;而当采用经典三回路过载驾驶仪时,则可以通过适当增大开环穿越频率、适当减小二阶阻尼或者增大一阶环节时间常数的方法来减小闪烁噪声下的脱靶量。

闪烁噪声; 比例导引; 开环穿越频率约束下极点配置; 脱靶量

0　引　言

目标闪烁是存在于雷达寻的导弹制导过程中的一种随机误差源,指由于扩展目标不同散射点产生的雷达回波信号相互干扰,使得回波信号相位波前失真,从而产生雷达导引头目标测角误差[1]。目标闪烁的根源来自目标回波信号的固有特性,难以通过对探测系统的设计来避免这种误差[2]。由于闪烁噪声的带宽与制导系统带宽接近,制导系统难以将其滤掉,使其成为末制导段影响导弹制导精度的主要随机误差源之一[3]。

国内外关于研究提高闪烁噪声下制导精度的文献比较多,主要分为两个方向:一个方向是从雷达导引头跟踪的角度,通过设计先进的滤波方法,来减小闪烁噪声对制导指令的影响;另一个方向则从宏观制导控制的角度,研究制导参数对闪烁作用下比例导引脱靶量的影响。

文献[4-8]具有一定代表性,主要研究闪烁噪声下雷达导引头对目标的跟踪,将其看作一个非高斯问题,采用了高斯混合卡尔曼滤波、鲁棒卡尔曼滤波、相互多模型等一系列滤波方法来提高目标跟踪精度,这类方法在提高跟踪精度的同时损失了制导系统的快速性,而且并没有明确证明这些方法提高了导弹的末制导精度。

文献[9-11]则主要通过采用蒙特卡罗方法和伴随法研究了闪烁噪声的影响,证明了闪烁噪声作用下的脱靶量不会随着末制导时间的增大收敛到零,提出了提高制导精度的一系列措施,例如降低比例导引有效导航比、减小末导段弹目相对速度等,但关于如何从控制系统设计的角度来降低噪声对制度精度的影响,尚未有明确的提法与分析。

本文建立了闪烁噪声作用下雷达寻的比例导引制导控制系统模型,并在模型中引入了平台导引头动力学;分析了采用两类常用控制系统时空地导弹的制导精度;从控制系统设计的角度,系统地研究了闪烁背景下提高雷达寻的制导精度的方法。对控制系统设计指标的权衡具有重要的参考意义。

1　闪烁噪声对制导指令的影响

1.1闪烁噪声的仿真

闪烁本质上是目标位置随机线偏差,反映到雷达导引头上则为随机视线角偏差;通过对大量实验中闪烁噪声的频谱分析发现,其属于低频有色噪声,可用白噪声通过一阶滤波器来近似[12]。因此工程上常用闪烁噪声引起的视线角均方根σ和一阶滤波器时间常数Tf来分别表征闪烁噪声的幅值与频率。

严格的白噪声是难以被模拟的,仿真中采用高斯分布伪随机序列来模拟白噪声,当伪随机序列的采样时间h远小于滤波器时间常数Tf时,可以将其视作白噪声[13],根据采样时间选取原则

(1)

取h=0.001s。

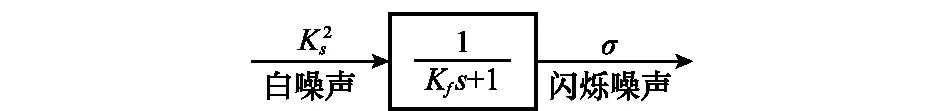
图1　闪烁噪声的仿真模型

(2)

得到白噪声的双边功率谱密度为

(3)

仿真时长取5s,仿真得到的闪烁噪声均方根为:σs=0.008rad×57.3=0.46°,闪烁噪声信号如图2所示。

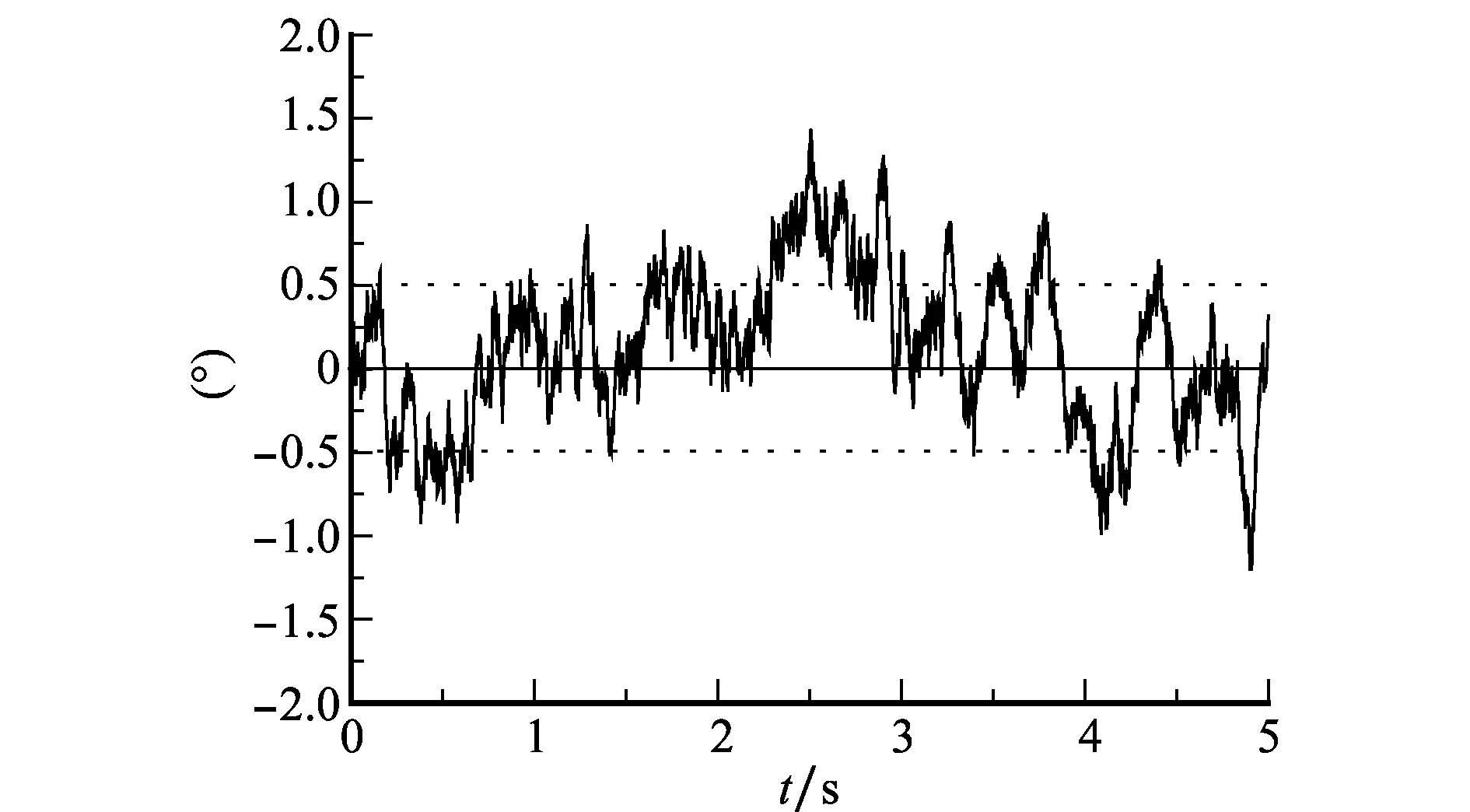
图2　仿真生成的闪烁噪声信号

1.2闪烁噪声对平台导引头制导指令的影响

图3　引入闪烁噪声的导引头近似动力学模型

噪声作用下的导引头角跟踪信号qs与输出的角速度制导指令信号如图4(a)所示。由于噪声频率与导引头频率接近,导致其对噪声的滤波作用较差,角跟踪信号qn能够响应闪烁噪声信号qs,从而使得制导指令信号受噪声的影响明显,如图4(b)所示。噪声对雷达制导系统的直接影响就是产生了较大的角速度制导指令偏差信号,根据比例导引制导律解析表达式[12]

(4)

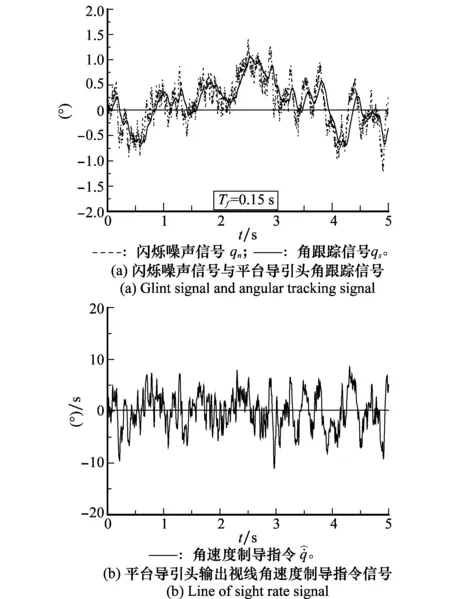
图4　闪烁噪声信号与平台导引头相关信号

制导指令偏差直接改变了进入控制系统的过载指令,由于导弹制导控制大回路难以通过负反馈闭环来消除闪烁噪声造成过载指令偏差带来的不利影响,因此闪烁噪声必将导致制导精度的下降。

2　闪烁作用下的比例导引制导模型

2.1雷达寻的比例导引制导模型建立

图5　闪烁噪声作用下的比例导引制导模型

2.2比例导引制导模型的伴随系统

求解噪声作用下的脱靶量主要有蒙特卡罗法和伴随法。蒙特卡罗法虽然直接在原制导系统的基础上进行实验,但是实验量很大,而且精度不高;伴随法是利用数学变换得到制导系统的伴随系统,通过一次仿真就可以得到不同末制导时间的脱靶量均方值。因此本文主要采用伴随法仿真比例导引脱靶量均方根σM。

采用伴随法对原制导系统进行变换,可以得到制导系统的伴随系统,具体步骤参考文献[13]。伴随模型如图6所示,其中Gs(s)和Gc(s)仍分别为导引头与控制系统动力学。分析模型可直接得出,闪烁噪声作用下的比例导引制导脱靶量与弹目相对速度Vc成正比,弹目相对速度越小,脱靶量越小。

图6　比例导引制导系统伴随模型

3　雷达寻的导弹控制系统设计

3.1比例导引制导体制下的控制系统

比例导引制导律产生过载指令,对应的控制系统为过载驾驶仪。目前工程上应用的典型过载驾驶仪主要有经典两回路过载驾驶仪、经典三回路过载驾驶仪等。

两回路过载驾驶仪存在静态响应误差,且受气动变化影响,但是由于其结构简单,容易实现,目前工程上仍在使用。三回路过载驾驶仪性能不受气动变化的影响,对高频噪声有较强的滤波能力,关键其可以降低雷达导引头天线罩斜率寄生回路的影响[16]。

两种控制系统的模型如图7和图8所示,模型中均忽略舵机动力学。模型中均忽略了舵机等硬件动力学。模型中Ks表示舵机增益,对尾舵控制方式,取为-1;对于鸭舵控制方式,取为1。c表示加速度计相对重心的超前安装距离。KA、Kg、ωI表示输出反馈增益,Kd表示闭环增益调节系数。

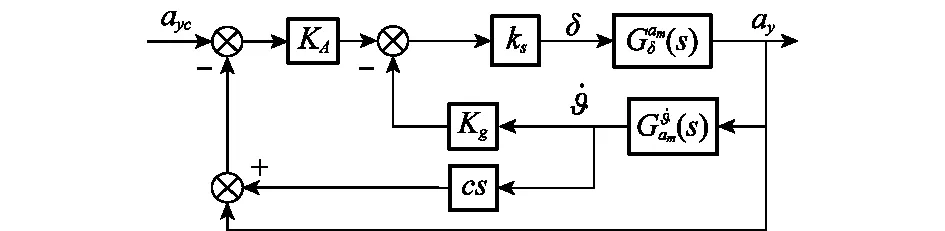
图7　经典两回路过载驾驶仪模型

图8　经典三回路过载驾驶仪模型

3.2开环穿越频率约束下的控制系统设计

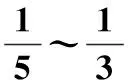
(5)

式中,ζs为舵机阻尼。若取ζs=0.7,舵机在开环频率处的相位滞后为[16.3°,27.7°],可见硬件动力学对控制系统频域性能影响明显。将开环穿越频率作为一项设计指标可以确保控制系统的频域性能。

为兼顾控制系统时域性能,将控制系统设计指标取为时域/频域的混合设计指标。两回路驾驶仪取为开环穿越频率ωCR1、闭环阻尼ζ1。三回路驾驶仪时域性能主要取决于一阶环节时间常数TIn,其值为0.10～0.3s,其二阶阻尼在0.7左右[19],因此三回路驾驶仪设计指标取为开环穿越频率ωCR2、一阶环节时间常数TIn和二阶频率阻尼ζ2。

表2给出了某典型空地导弹的气动数据。当前硬件发展水平下典型舵机的频率ωs=220rad/s,阻尼ζs=0.65。

表2　弹体气动数据

两回路、三回路驾驶仪设计指标分别设为4组、5组,具体分别见表3、表4。

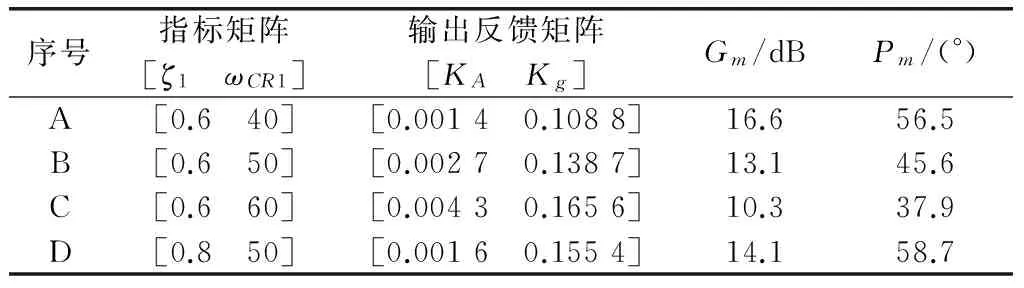
表3　两回路驾驶仪设计指标及结果

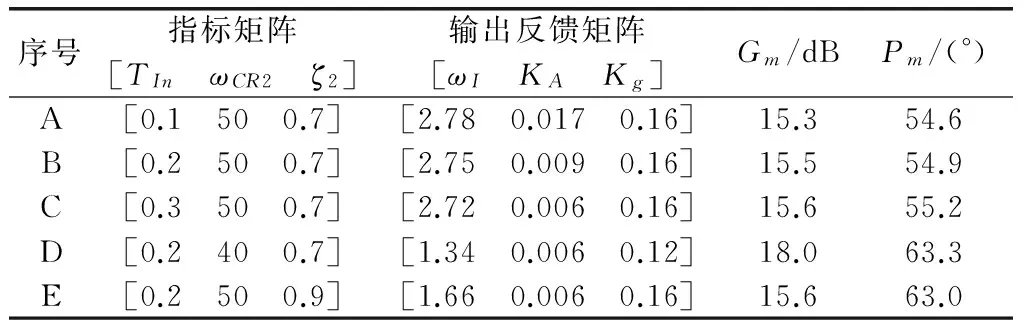
表4　三回路驾驶仪设计指标及结果

控制系统其他指标确定时,两回路/三回路驾驶仪的开环穿越频率ωCR与其闭环二阶频率ωc之间存在一一映射的关系,表示为

(6)

利用这个映射关系,可得出两回路/三回路驾驶仪的二阶震荡频率。从而将时域/频域混合设计指标转换为控制系统的期望闭环极点,通过传统的极点配置方法完成控制系统设计。

3.3线性系统输出反馈的极点配置

两回路与三回路驾驶仪的极点配置方法没有本质区别,此处仅阐述两回路过载驾驶仪的极点配置设计思想。

从而可将弹体模型描述为状态空间的形式,即

(7)

y=Cx+Du

(8)

两回路作为典型的线性系统,尽管状态反馈可实现其极点任意配置,但由于攻角信息难以直接测量,因此导弹控制系统全状态反馈不能实现,而当全状态可观时,可将全状态反馈转换为输出反馈,通过输出反馈实现极点配置的目的。

定义状态反馈为

(9)

根据图7两回路驾驶仪模型将输出反馈定义为

(10)

经过简单推导容易得到二者关系为

(11)

式(11)成立的条件是(I-KC-1D)-1,即系统全状态可观。从而可得出两回路驾驶仪的两个输出反馈增益的具体形式为

(12)

3.4设计指标对控制系统性能的影响

为研究问题本质,此处不考虑c。两回路驾驶仪的开环穿越频率ωCR一般在开环弹体自振频率ωn的5倍左右[13],同时由于驾驶仪二阶频率远大于开环弹体阻尼,即

(13)

从而可得

(14)

(15)

根据图7推导两回路驾驶仪开环传函为

(16)

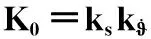
(17)

(18)

令幅频特性等于1,结合式(15)可得到穿越频率与开环弹体频率的近似关系为

(19)

驾驶仪闭环传函可表示为

(20)

同时闭环传函还可表示为

(21)

式中，ωc表示驾驶仪二阶频率。两种形式表达分母相等,结合式(19)可得到方程组

(22)

利用方程组式(22)可解得

(23)

结合式(14)、式(15),式(23)可近似为

(24)

将式(24)代入式(17),可得到由设计指标表示的相位裕度为

(25)

另外,驾驶仪阶跃响应上升时间[20]表示为

(26)

将式(24)代入式(26),得到

(27)

经过类似的理论推导可得到由设计指标表示的三回路驾驶仪相位裕度为

(28)

以及上升时间为

(29)

分析式(25)和式(27),对于两回路驾驶仪,增大开环穿越频率或减小闭环阻尼,均会降低系统的稳定裕度,同时使得系统阶跃响应上升时间减小,带来时域响应速度的提高。

分析式(28)和式(29),对于三回路驾驶仪,一阶时间常数TIn对稳定裕度基本没有影响,增大二阶阻尼ζ2或减小开环穿越频率ωCR2均可以提高系统稳定裕度;同时,系统的时域响应速度主要取决于一阶环节时间常数,而二阶阻尼和穿越频率对其没有明显影响。

取不同的设计指标分别设计两回路、三回路驾驶仪,得到对应的反馈增益、稳定裕度(考虑舵机动力学)分别如表3、表4所示。图9、图10为两种控制系统单位阶跃响应曲线。经过对比不同指标下驾驶仪稳定裕度和时域响应曲线,验证了上述结论的正确性。

图9　两回路驾驶仪时域阶跃响应

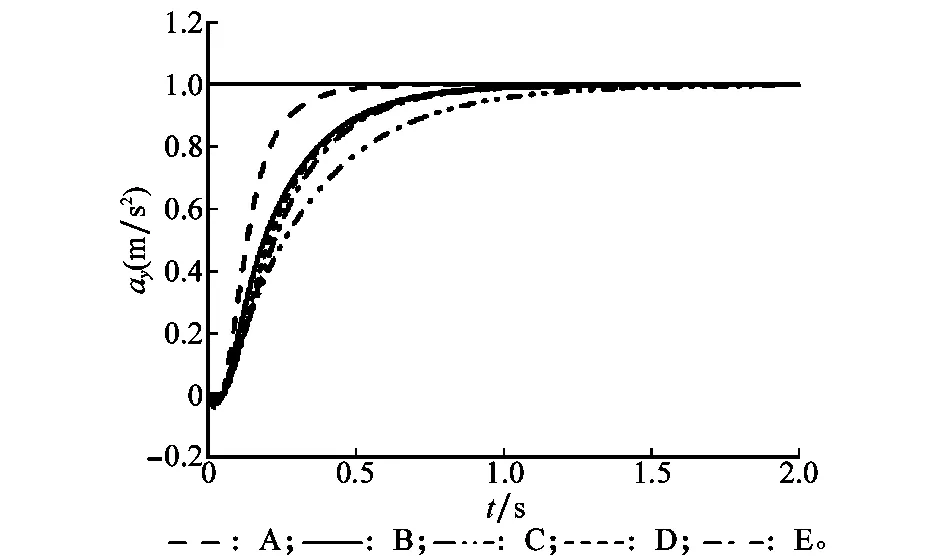
图10　三回路驾驶仪时域阶跃响应

4　提高制导精度的控制策略研究

4.1两回路/三回路驾驶仪下的比例导引脱靶量

空地作战方式下,采用伴随法,研究闪烁噪声作用下的比例导引制导精度,此时弹体速度远大于目标速度,弹体速度约等于弹目相对速度。制导模型中的控制系统采用表3、表4中不同设计指标下的两回路、三回路过载驾驶仪,得到九组不同动力学制导系统模型,其时间常数如表5所示。模型的仿真参数如表6所示。此处闪烁噪声作用下的比例导引脱靶量指的是脱靶量均方根。

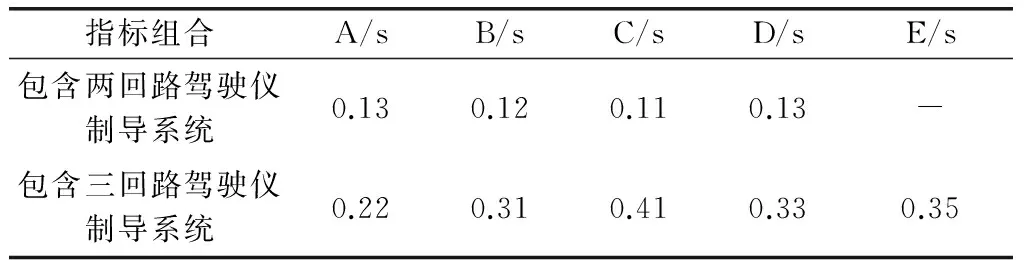
表5　制导控制系统动力学时间常数

表6　系统仿真参数设定

当导弹控制系统为两回路驾驶仪时,分析仿真结果如图11和图12所示。

图11　控制系统为两回路驾驶仪时的脱靶量(N=3)

图12　控制系统为两回路驾驶仪时的脱靶量(N=4)

(1) 闪烁噪声产生的脱靶量并不随着末制导时间的增大而减小到零,而是随着其增大而增大,在10倍左右的制导时间常数时收敛到一个稳定值;有效导航比N越大,脱靶量稳定值越大;

(2) 适当减小闭环阻尼ζ1,脱靶量减小;

(3) 当开环穿越频率在50 rad/s左右时,脱靶量达到极小值。

当导弹控制系统为三回路驾驶仪时,分析得到的仿真结果如图13和图14所示。

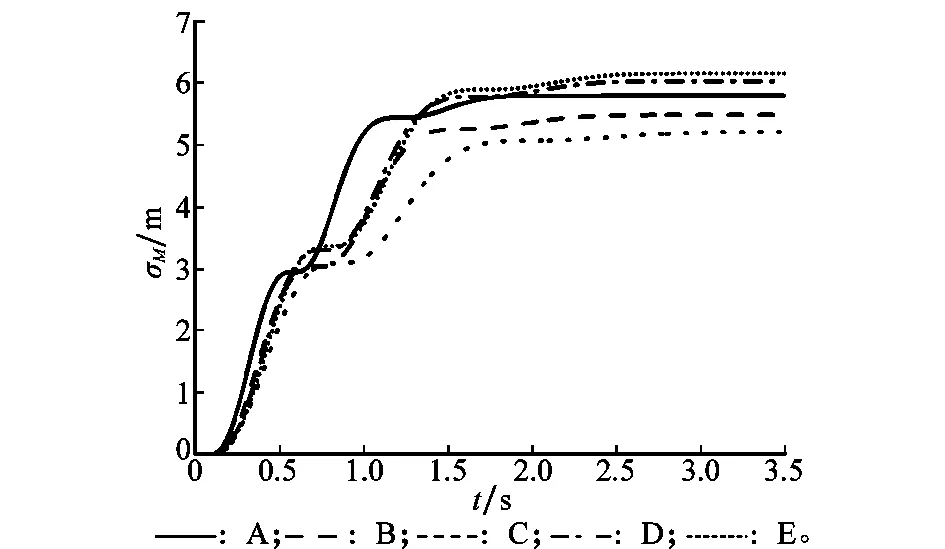
图13　控制系统为三回路驾驶仪时的脱靶量(N=3)

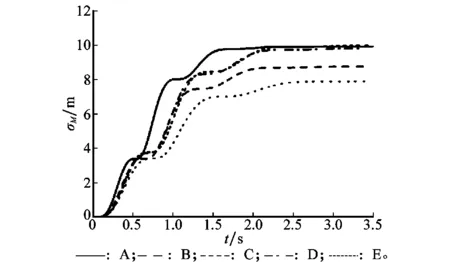
图14　控制系统为三回路驾驶仪时的脱靶量(N=4)

(1) 脱靶量同样在10倍制导系统时间常数处收敛到稳定值,有效导航比N越大,脱靶量稳定值越大;

(2) 一阶环节时间常数越大,脱靶量越小;

(3) 开环穿越频率越大,二阶阻尼越小,脱靶量越小。

4.2闪烁背景下比例导引制导精度改进方案

综合之前的分析与仿真,从制导律的角度提高闪烁噪声下制导精度的方案为:降低有效导航比,降低末制导段弹目相对速度;同时降低有效导航比可能导致末端弹体过载饱和,降低弹目相对速度则可能降低弹头的打击效能。

从控制系统设计的角度,当控制系统为两回路驾驶仪,制导精度改进方案为:减小闭环阻尼指标,适当增大开环穿越频率指标。当控制系统为三回路驾驶仪时,制导精度改进方案为:增大一阶时间常数指标,减小二阶阻尼指标,增大开环穿越频率指标。

在调节控制系统设计指标提高制导精度的同时,又影响控制系统时域和频率性能。

5　结　论

低频的闪烁噪声进入平台导引头后,首先引起角速度制导指令的变化,进而产生比例导引脱靶量,而且脱靶量不随末制导时间的增大收敛到零。

采用开环穿越频率约束下极点配置的方法设计了典型两回路、三回路过载驾驶仪,研究了控制系统设计指标对闪烁噪声背景下比例导引制导精度的影响。

研究结果表明:从控制系统设计角度,通过增大开环穿越频率、增大一阶时间常数或降低阻尼指标的方法，均可以实现闪烁噪声下制导精度的提高;同时,又会带来控制系统时域或频域性能的损失。工程师应该综合考虑,在制导精度指标与控制系统的性能之间进行权衡,以求达到二者的一个最优组合。

采用比例导引制导律时,低频闪烁噪声对导引头角速度信号影响较大,而对角度信号影响相对较小,未来可以研究采用角度制导律代替比例导引来提高闪烁噪声存在时的制导精度。

[1] Kajenski P J. Comparison of two theories of angle glint: polarization consideration[J].IEEETrans.onAerospaceandElectronicSystems, 2006, 42(1): 206-210.

[2] Sui M, Xu J. Angular glint calculation via adaptive cross approximation algorithm[C]∥Proc.oftheIEEEInternationalSymposiumonAntennasandPropagation, 2011: 2746-2749.

[3] Ananthasayanam M R, Sarkar A K, Tiwari P K. Nonlinear observer state estimation from seeker measurements and seeker-radar measurements fusion[C]∥Proc.oftheAIAAGuidance,Navigation,andControlConferenceandExhibit,2005:6066-6090.

[4] Gordon N, Whitby A. Bayes approach to guidance in the present of glint[J].JournalofGuidance,Control,andDynamics, 1999, 22(3): 478-485.

[5] Jinwhan K, Monish T, Menon P K. Particle filter for ballistic target tracking with glint noise[C]∥Proc.oftheAIAAGuidance,Navigation,andControlConference, 2010: 7881-7892.

[6] Hu H T, Jing Z L, Li A P. Target tracking in glint noise using a MCMC particle filter[J].JournalofSystemsEngineeringandElectronics, 2005,16(2): 305-309.

[7] Rusnak I. Bounds on the miss of multiple-model-based terminal guidance laws[J].JournalofGuidance,Control,andDynamics, 2014,37(3): 729-940.

[8] Bilik I, Tabrikian J. Target tracking in glint noise environment using nonlinear non-Gaussian Kalman filter[C]∥Proc.oftheIEEERadarConference, 2006: 282-287.

[9] Zhang H, Lin D F, Qi Z K, et al. Influence of radar guidance system noise on precision of guidance and control[J].JournalofSystemSimulation, 2008, 20(5): 1295-1233.(张宏,林德福, 祁载康, 等. 雷达制导系统噪声对制导精度的影响[J].系统仿真学报,2008, 20(5): 1295-1233.)

[10] Lin D F, Shen H, Qi Z K. Influence of target glint on the precision of guidance and control[J].TransactionsofBeijingInstituteofTechnology, 2007, 27(1): 9-12.(林德福,沈浩,祁载康. 目标闪烁对制导精度的影响[J].北京理工大学学报,2007,27(1):9-12.)

[11] Xia Q L, Liu Y Y, Qi Z K, et al. Study of proportional navigation guidance error caused by angular noise and glint effect[J].SystemsEngineeringandElectronics, 2008, 30(8): 1460-1463. (夏群力,刘轶英,祁载康,等. 由角噪声及目标闪烁引起的比例导引制导误差研究[J].系统工程与电子技术,2008,30(8): 1460-1463.)

[12] Garnell P.Guidedweaponcontrolsystem[M]. London: Pergammon Press, 1980: 231-232.

[13] Zanchan P.Tacticalandstrategicmissileguidance[M]. 6th ed. Reston, VA: Progress in Astronautics and Aeronautics, 2012.

[14] Song T. Research on disturbance rejection rate and online state estimation technology of seekers applied in air-to-air surface-to-air missiles[D].Beijing: Beijing Institute of Technology,2014.(宋韬.新一代空空/地空导弹导引头隔离度及在线状态估计与补偿技术研究[D]. 北京:北京理工大学,2014.)

[15] Luo P F.Analysisandprocessingofrandomsignal[M]. Beijing: Tsinghua University Press,2006:123-125.(罗鹏飞.随信号分析与处理[M].北京:清华大学出版社,2006:123-125.)

[16] Wang H, Lin D F, Qi Z K. Design and analysis of missile three-loop autopilot with pseudo-angle of attack feedback[J].SystemsEngineeringandElectronics,2012,34(1):129-135.(王辉,林德福,祁载康.导弹伪攻角三回路驾驶仪设计分析[J].系统工程与电子技术,2012,34(1):129-135.)

[17] Fan J F, Lin D F, Qi Z K, et al. Design and analysis of a two-loop autopilot[J].SystemsEngineeringandElectronics, 2008, 30(12): 2447-2450. (范军芳,林德福,祁载康,等. 两回路自动驾驶仪设计与分析[J].系统工程与电子技术,2008, 30(12): 2447-2450.)

[18] William N F, Mark N L. How autopilot requirements constrain the aerodynamic design of homing missiles[C]∥Proc.oftheAmericanControlConference, 1984: 716-730.

[19] Devaud E, Siguerdidjane H, Font S. Some control strategies for a high-angle-of-attack missile autopilot[J].ControlEngineeringPractice, 2000,8(8): 885-896.

[20] Hu S S.Automaticcontroltheroy[M]. Beijing: Science Press, 2005: 80-82.(胡寿松.自动控制原理[M]. 北京:科学出版社,2005: 80-82.)

Influence of two-loop/three-loop autopilot on precision of guidance and control with glint noise

WANG Guang-shuai, LIN De-fu

(School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)

Glint noise comes to one of the main random error sources for the terminal radar guidance system. In this kind of background, the improvement of impact precision for radar guided missile in the presence of glint noise is studied, from the control system design perspective. With glint noise as its input, noisy model of guidance and control including approximate gimbal seeker dynamics is established. The control system design index is chose within both time and frequency domain, and then the pole placement design procedure with open-loop crossover frequency constraint for typical two-loop and three-loop autopilots is accomplished. The effect of design index on the miss distance of impact is estimated. The results show that when two-loop autopilot is used in the proportional guidance and control system, properly increasing open-loop crossover frequency index, or softly decreasing the system damping index could always lead to more precise impact, and when three-loop autopilot is adopted, enlarging the simple phase-lag element (three-loop autopilot) is the third effective way besides the two ones proposed before.

glint noise; proportional navigation; the pole placement design procedure with open-loop crossover frequency constraint; miss distance

2015-04-20；

2015-09-09；网络优先出版日期：2016-02-15。

国家自然科学基金(61172182)资助课题

TJ 765.2

A

10.3969/j.issn.1001-506X.2016.08.24

王广帅(1987-),男,博士研究生,主要研究方向为飞行器制导与控制。

E-mail: justbeatit@bit.edu.cn

林德福(1971-),男,教授,博士,主要研究方向为飞行器制导与控制。

E-mail: lindf@bit.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160215.1437.008.html