混合蛙跳算法自适应参数调整改进策略

2016-08-15肖莹莹林廷宇李伯虎侯宝存施国强

系统工程与电子技术 2016年8期

肖莹莹, 林廷宇, 李伯虎, 侯宝存,3, 施国强,3

(1.北京市复杂产品先进制造系统工程技术研究中心, 北京仿真中心, 北京 100854;2. 复杂产品智能制造系统技术国家重点实验室, 北京电子工程总体研究所, 北京 100854;3. 航天系统仿真重点实验室, 北京仿真中心, 北京 100854)

混合蛙跳算法自适应参数调整改进策略

肖莹莹1,2, 林廷宇1,2, 李伯虎2,3, 侯宝存1,2,3, 施国强1,2,3

针对基本混合蛙跳算法(shuffled frog leaping algorithm, SFL)在求解高维复杂问题时的不足,本文提出一种自适应参数调整的改进策略。首先,利用变公比数列分析了SFL更新轨迹的收敛性;在此基础上,利用系统稳定性分析方法,提出在SFL更新公式中基于比例系数和适应度标准差来自适应调整更新的方法。最后,基于3组共8个标准测试函数将本文改进SFL与基本SFL和4个改进型粒子群优化算法(particle swarm optimization,PSO)作对比,验证了本文改进策略对各类复杂函数的高效性;同时,对比了改进SFL与基本SFL和wPSO在求解高维问题时的性能,验证了改进SFL对高维问题求解的有效性。

混合蛙跳算法; 收敛性; 自适应参数调整; 智能计算

0　引　言

作为新兴的计算智能技术,以蚁群优化算法和粒子群优化算法为代表的群体智能优化技术受到了世界各国科研工作者的广泛重视,通过对它们进行深入和细致的研究,取得了丰硕的研究成果。这种基于种群的进化算法具有隐含的并行特征,可以在单次模拟过程中得到多个解,因此非常适合求解多目标优化问题。目前,群体智能技术在多目标优化、数据分类、模式识别、系统建模、决策支持、系统辨识、信号处理、过程控制等方面得到广泛应用,展现了群体智能技术解决优化问题的独特优势。

混合蛙跳算法(shuffled frog leaping,SFL)是由M. Eusutl和E. Lansey于2003年提出的基于群体智能的新型优化算法[1],它结合了粒子群优化算法(particle swarm optimization,PSO)良好的全局搜索能力和元算法Metric较强的局部搜索能力,具有实现简单、适应性强、鲁棒性好等优点,是群体智能优化技术研究与发展的重要方向,已经应用于多项工程优化问题[2-4]。此外,文献[5]通过比较遗传算法(genetic algorithm,GA)、文化基因算法(memetic algorithm,MA)、粒子群算法(particle swarm algorithm,PSO)、蚁群算法(ant colony optimization,ACO)和SFL,指出PSO在多数单模平滑/无噪声问题上有很好的求解成功率和求解质量,但在某些复杂奇异/多模问题上不如SFL。总的来说,PSO和SFL具有与问题无关的特性,很适合应用于复杂工程问题求解。

但和PSO算法一样,基本SFL算法也存在早熟收敛和收敛较慢的难题[6]:随着迭代次数的增加,个体之间变得越来越相似,容易陷入局部最优,出现早熟收敛。由于算法权系数变化范围固定,无法自适应地调整搜索步长,在初始状态寻找次优解时速度较慢,在次优解附近精确定位最优解时需要很多次迭代,导致算法收敛较慢。

为提高SFL的收敛性,加快其收敛速度,国内外学者先后做出一些改进,例如:文献[7]将SFL与遗传算法结合,并使用K邻域聚类改进选择算子,文中使用11种典型问题测试了混合算法的性能。文献[8]通过对SFL算法收敛行为的分析,引入一种新的认知组件到每个个体中,增强个体的自主决策能力,文中使用6个benchmark问题验证了改进算法的效率。文献[9]受到离散SFL算法启发,通过改进蛙群的分组方法得到一种新的改进算法,通过与标准SFL的性能对比验证了改进策略的有效性。文献[10]通过扩展跳跃步长范围和引入跳跃惯性分量,有效地改善了跳跃规则,但是所提出的跳跃规则缺少理论依据。

这些改进策略有些缺乏理论支撑,无法适用于求解所有类型的问题;有些在做算法比较时使用的测试问题较为简单(维数较低/单模问题),无法反映求解真实多目标高维问题的效率。因此,本文后续部分着重以SFL的收敛性理论分析为基础,给出合理的改进策略,并使用丰富的测试函数与目前流行的算法做对比,保证改进策略在求解后续复杂问题时依然有效。

1　基本混合蛙跳算法

基本SFL算法原理[1]如下图1所示。

步骤 1初始化算法条件,包括种群大小P、种群个数M和步长;

步骤 2随机产生包含P只青蛙的群体,并计算每只青蛙的适应度;

步骤 3迭代搜索开始:将整个蛙群根据适应度大小排序后划分成M个族群,并对每个族群执行it次局部搜索以更新本族群的最差解(记为Xw) (具体流程如图1中所示A-B)。

步骤 4所有族群完成局部搜索后,将所有青蛙混合在一起重新分组,当次迭代结束;

步骤 5判断当前结果是否满足收敛条件,若不满足则重新排序并划分族群执行上述局部搜索过程,若满足则算法结束。

步骤3局部搜索是SFL算法的核心,其核心思想是根据组内的最优解Xb和群体最优解Xg来更新最差解Xw。标准SFL算法的第k次迭代的更新策略具体描述如下:

(1)

(2)

(3)

图1　基本SFL算法流程图

由上述算法的基本流程可知,SFL算法是一种通过不断迭代利用多个个体在搜索空间中寻找最优解的随机群体优化算法。决定SFL算法求解效率的核心是局部搜索的更新策略,为了保证在有限次迭代中找到满足收敛精度的解,算法必须在逐步收敛的前提下扩大解的随机性,保持尽可能多地遍历整个搜索空间,避免“早熟”,提高收敛精度和全局搜索能力。同时,若无限制的提高随机性,则算法会陷入无规则的尝试中,浪费大量计算时间,降低了算法的收敛速度。因此,收敛速度和收敛精度的平衡是保证SFL能够适用于应用问题要解决的重要方面,下面将详细分析SFL算法的收敛性,以得到平衡精度和速度的改进策略。

2　收敛性分析

为便于分析,假设Xb=Xg,且为了分析新解的可变轨迹,将式(1)～(3)扩展描述为

第k次迭代:

(4)

第k+1次迭代:

(5)

由式(4)和(5)得

(6)

记ΔXk+1=Xk+1-Xk,式(6)整理为

(7)

则有

(8)

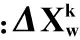
结论 2SFL算法的收敛速度和精度与系数α，β和l有关。根据l合理的调节α，β,可以在保证算法按概率收敛的前提下,具有更快的收敛速度,使算法具有更强的全局搜索能力和全局/局部平衡能力。

假设α是α∈[αmin,αmax]范围的随机数,β是β∈[βmin,βmax]范围的随机数,那么q=(α+βl)可以划分为2个区域:

(9)

式中,{q|0<|q|<1}是保证数列收敛的区间;{q||q|≥1}是数列不收敛的区间,用于增强解的随机性避免早熟。因此系数α、β和l决定了q落入收敛区间0<|q|<1的概率,即

(10)

l值是迭代中间量,在概率表达式P=f(α,β|l)中属于先验知识,讨论中可假设为常数,则P只与α和β有关,即P=f(α,β)。因此可以通过调节α和β来平衡收敛速度和精度,使得当P很大时,算法沿较强的收敛轨迹运动;P减小时,跳出局部最优解的能力加强。

综上所述,在迭代过程中,根据群体的状态和中间量l合理设置α和β的随机区间,以自适应的改变公比q的取值范围,可以扩大全局搜索能力,保证算法具有较快的收敛速度和较高的收敛精度。

3　改进策略

本节将从控制理论中的系统稳定性分析理论出发,定量给出SFL搜索性能与α和β的取值范围区间的关系分析,得到α和β的取值范围确定准则。为便于表述,最差解的更新公式可表示为

(11)

(12)

则由式(11)～式(12)得到

(13)

该方程可以看作是系统的差分方程表达形式,利用Z变换原理,得到系统传递函数

(14)

(15)

3.1比例系数l的作用

比例系数l代表了本次迭代中,最差解的变化速率与(局部/全局)最优解的变化速率之间的关系,是表征系统随机性的重要特征。因此，根据l取值范围,更新策略分析如下:

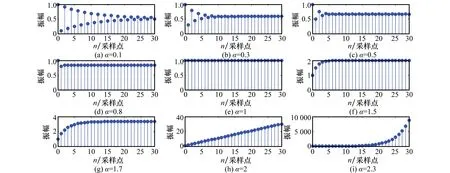
图2　不同α的阶跃响应

当0<α<1,阶跃响应是逐步收敛的,并且α越大,收敛速度越快;当α=1,阶跃响应是完全收敛的,最差解直接跳到最优解位置;当1<α<2,阶跃响应是逐步收敛的,并且α越小,收敛速度越快;当α≥2,阶跃响应是发散的,并且α越大,发散速度越快。

图2所示不同α的阶跃响应结果进一步验证了当β=1且α∈(0,2),最差解Xw将在有限迭代次数内收敛到最优解Xb,且当α越靠近0或2,收敛速度就越慢。因此,可将α的取值范围设置为α∈(1-Δ,1+Δ),则Δ∈(0,1),且Δ越小,收敛速度越快。同时,为了保持算法具有一定的随机性,避免陷入某个局部解无法突破,可以将β扩展成(0.95,1.05)的随机数,以增强算法的全局搜索能力。此时,最差解Xw的变化区域是围绕着最优解Xb的一个狭长四边形(如图3所示)。

图3　当l>0时最差解的变化区域

总之,当l>0时,α和β可以使用公式(16)生成,即

(16)

此时,新解的变化区域面积为S=0.1×2Δ=0.2Δ。

图4所示不同β的阶跃响应结果进一步验证了当α=1 且β∈(0,2),最差解Xw将在有限迭代次数内收敛到最优解Xb,且当β越靠近0或2,收敛速度就越慢。因此,可将β的取值范围设置为β∈(1-Δ,1+Δ),则Δ∈(0,1),且Δ越小,收敛速度越快。同时,为了保持算法具有一定的随机性,避免陷入某个局部解无法突破,可以将α扩展成(0.95,1.05)的随机数,以增强算法的全局搜索能力。此时,最差解Xw的变化区域是围绕着D=(Xb-Xw)或D=(Xg-Xw)的狭长四边形(见图5)。

总之,当l<0时,α和β可以使用式(19)生成,即

(19)

图4　不同β的阶跃响应

图5　当l=0时最差解的变化区域

总之,当l=0时,α和β可以使用式(17)生成,即

(17)

此时,新解的变化区域面积为S=0.1×2Δ=0.2Δ。

(18)

为求解上述不等式,图6给出了不同Δ取值下极点位置随β的变化曲线。从图中看出,不论Δ如何取值,只要β∈(Δ,2-Δ),则可满足极点位于单位圆内的要求(红线所示区域)。

图6　不同Δ取值的极点位置

此时,新解变化区域是与Δ相关的平行四边形(见图7),面积为S=2Δ×(2-2Δ)=4Δ-4Δ2,S∈(0,1)。Δ越小,该四边形越是朝着纵向方向压缩,变成围绕D=(Xb-Xw)或D=(Xg-Xw)的狭长四边形;反之,该四边形越是朝着横向方向压缩,变成围绕最优解的狭长四边形。当Δ=0.5时,面积最大且为等边四边形。

因此,随机产生Δ,并使用公式(19)生成α和β可以保证算法保持一定的随机性且收敛。为了进一步明确Δ的取值对系统响应的影响,图8给出了不同Δ条件下的阶跃响应曲线。

图7　当l<0时最差解的变化区域

图8　不同Δ条件下的阶跃响应

如上图8所示,每行代表某个Δ随机产生的3组α和β的系统阶跃响应,包括Δ=0.1,Δ=0.5和Δ=0.9 3种情况。从图中9个响应曲线发现,所有响应曲线均在有限步长内收敛。同时,收敛速度是随机的,如图最大为25步。因此,进一步验证了使用公式(19)随机产生α和β可以平衡全局搜索能力和局部搜索效率。

总之,从比例系数的3种情况阶跃响应分析可以得到如下结论:

(1) 使用不同方法产生系数α和β决定了最差解的进化特性,从而影响了整个群体的行为特征,例如保持更大的随机性以增强全局搜索能力,或加速收敛速度保持收敛效率。

(2) 基于比例系数l的取值,合理调节Δ,并基于式(16)、式(17)、式(19)随机生成α和β可以平衡算法的全局收敛能力和局部搜索效率。Δ的调节方法将在下节详细论述。

3.2适应度标准差的作用

如上所述,本文改进策略的基本原则是在每次局部搜索的迭代中,根据l取值自适应选择不同的系数取值范围来更新最差解,即

(20)

(21)

这种改进策略可以保证算法在有限步长内收敛,并保持一定的随机性,很好的平衡了全局搜索能力和收敛效率。但同时应该注意到,上述方法中Δ是一定范围变化的随机数,而收敛步长与Δ的取值有关,造成阶跃响应的收敛步长与算法当前状态无关,无法根据群体的聚集程度和最优解的更新频率等自适应地扩大/缩小步长,因此无法加快收敛速度。

为自适应调整Δ以加快收敛速度,本节引入全局最优解序列Xg(k)在当前迭代附近时间窗子序列标准差stdJi来度量算法的当前状态,作为调整Δ的依据。stdJi是反映Xg(k)离散程度的统计值,可预测全局最优解的更新频率。当Xg(k)变化缓慢(或几次迭代均未更新)时应增强随机性使得新解具有突破当前位置的能力,来避免陷入局部最优;反之,应保持一定的随机性来跟随最优解,在其附近探索新解。

(22)

式中,Ji是全局最优解在第i-th迭代的适应度值。所以,当stdJi较小时,Xg(k)变化缓慢;当stdJi较大时,Xg(k)变化较快。因此,使用stdJi调节Δ的取值方法如下式(23)所示。

(23)

总之,根据迭代过程中的stdJi,实现自适应调节Δ,是本文加快收敛速度的策略。

3.3基于比例系数和适应度标准差的调节策略

综上所述,本文改进策略可以总结为一种根据比例系数l和适应度标准差stdJi来自适应调整更新系数α和β的技术。详细的系数产生策略如表1所示。

表1给出了根据比例系数l和适应度标准差stdJi选择最差解Xw更新公式的系数α和β及Δ的具体方法。直观上看,对每行l<0情况下Xw的可变范围要大于l>0,意味着无论标准差stdJi是多少,都需要减小随机性来确保最差解能在最优解附近区域搜索。在每一列,stdJi越小,Δ的取值范围越大,意味着需要增强随机性来确保最差解能在更大区域搜索,使得算法具有跳出当前最优解的能力,避免陷入局部最优。

为了进一步验证本文改进策略对收敛特性的影响,下图9给出了不同l和Δ条件下的系统阶跃效应。

表1　自适应系数调整策略

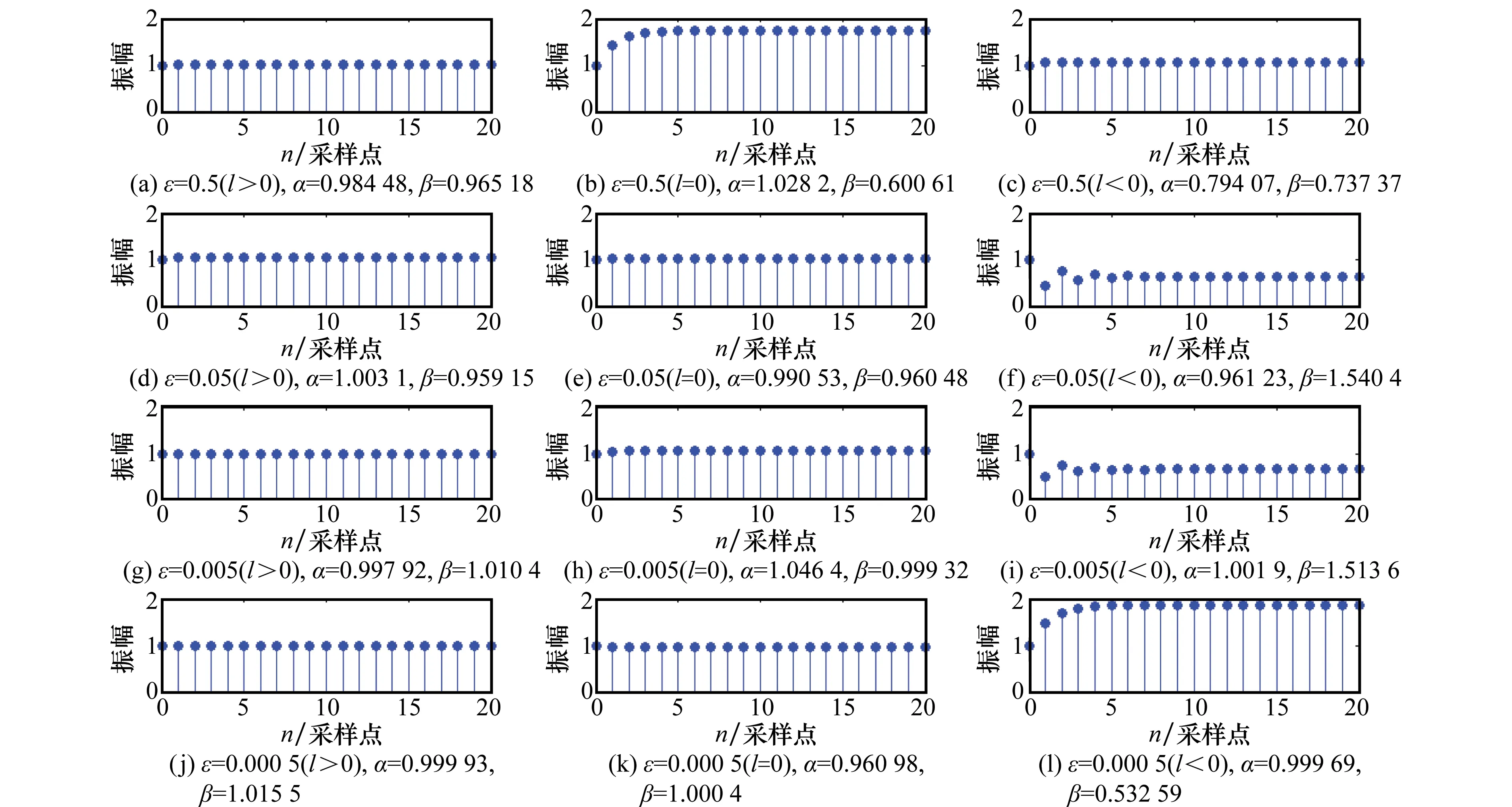
图9　不同l和Δ条件下的系统阶跃效应

图9所示阶跃响应验证了本节所论述的观点。当l>0时,从阶跃响应可以看出,系统在1～2步内快速稳定收敛;当l<0时,则需要1～7步才能收敛。由此说明l<0时的系统随机性保持的很好,达到稳定所需的步长是随机的;而l>0在一定随机性下将以更快的速度收敛。

总之,比例系数l和适应度标准差stdJi是两个重要的指标,分别对算法的收敛性和收敛速度产生影响。本文提出的改进策略是一种动态平衡新解可变范围和收敛速度的方法。当迭代过程中,群体聚集度高容易陷入局部最优时,通过调节Δ增大系统的随机性;反之,应该更加关注最优解附近区域避免不必要的尝试,以此来提高收敛速度。

4　性能测试

4.1不同特性的标准测试集

为了测试改进混合蛙跳算法对不同问题的求解性能,本文根据文献[11-14],选择3组共8个标准测试函数(如表2)做对比。包括:①单模函数测试组:F1 Sphere测试收敛速度;F2 Rosenbrock评价优化算法执行效率;F3 Ackley函数在狭长的全局最优点周围拥有很多局部极值点,测试全局搜索能力;F4 Easom是一个非线性函数,全局最小解分布在很窄的洞中而外围几乎是平面,很难找到最优解。②多模函数测试组:F5 Rastrigrin测试种群多样性;F6 Griewank测试收敛速度;F7 Schwefel包含很多峰值且全局最小值周围有很平滑的区域,很难求解。③带噪声多模函数:F8 Levy有很多局部最小点,同时含有噪声,常用来测试多模噪声环境下的算法搜索性能。

表2　标准测试函数

为评估改进混合蛙跳算法的性能,本文选取标准SFL和4种PSO算法做对比。① wPSO:由Shi和Ebehart R于1998年提出的时变惯性权重PSO算法[15];② cPSO:由Clerc和 Kennedy于2002年提出的带约束因素的改进PSO算法[16];③ vPSO:由Y. Volkan于2012年提出的多频率震动PSO算法[17];④ clPSO:由Liang于2006年提出的带复杂自学习的PSO算法[18]。所有算法参数设置如表3所示。

对上述测试函数,所有算法都独立执行30次。算法使用Matlab 2009b实现,运行在Intel Core i5处理器(2.5 GHz)/4GB RAM的PC机上。表4给出了运行结果,分别从30次运行结果的最差适应度(Worst)、最好适应度(Best)、平均适应度(Mean)、成功率(Suc.)和运行时间(Time)5个方面做对比。需要注意的是,评价标准解为0的测试函数是否求解成功时,本文假设当求解精度高于10-8就认为本次运行求解成功。下图10同时给出了不同测试函数的运行最好的一次求解结果的收敛曲线。

表3　算法的参数设置

图10　同测试函数的收敛曲线

算法测试函数评价wPSOcPSOvPSOclPSOBasicSFLMSFLF1SphereWorst11.3143184.56112.2716e-0571.4222e-0151.4364e-53.055e-110Best0.0275450.735511.1908e-0697.4753e-0181.6565e-81.3556e-154Mean2.352931.48951.3678e-0582.3297e-0162.6292e-0061.0183e-111Suc.(%d)00100%100%0100%Time/s1.20981.14531.25144.722317.920332.1029F2RosenbrockWorst00.0390079.9104e-0168.9014e-0100.0581450Best007.7835e-0211.5306e-0142.6059e-0060Mean00.00136195.1948e-0172.5287e-0100.00627990Suc.(%d)100%86.7%100%100%0100%Time/s0.23940.210031.04573.625118.133932.4479F3AckleyWorst3.22288.6132.814317.92153.2638e-0053.5527e-015Best3.5527e-0150.02451200.171961.5737e-0090Mean0.575191.75980.3356611.34012.0342e-0062.3685e-016Suc.(%d)73.3%083.3%016.7%100%Time/s1.28751.26321.06674.204517.33930.8249F4EasomWorst-8.0683e-005-8.1102e-005-10-1-1Best-1-1-1-0.99999-1-1Mean-0.96667-0.72622-1-0.96296-1-1Suc.(%d)96.7%50%100%0100%100%Time/s0.238530.999030.445573.539217.156931.6668F5RastrigrinWorst25.869429.209816.91887.225930.34060Best2.98495.98512.9850.711042.98490Mean12.513914.10378.75693.483411.47740Suc.(%d)00000100%Time/s1.07751.13171.10544.678416.883130.6665F6GriewankWorst2.76883.17450.5516633.95180.375040Best0.278350.637480.04189610.30820.0503160Mean1.2341.67760.2683821.96680.157930Suc.(%d)00000100%Time/s1.4331.37811.38015.061617.438730.8855F7SchwefelWorst-601.0891-572.6518-620.8247-601.0886-719.5274-837.9658Best-837.9658-837.9657-837.9658-837.9657-837.9658-837.9658Mean-710.1637-691.5232-758.2083-766.6481-833.6939-837.9658Suc.(%d)13.3%06.7%063.3%100%Time/s1.2371.19451.25323.716417.370731.8599F8LevyWorst-147.2612-146.8709-166.9959-186.5909-170.5308-186.3406Best-186.7309-186.7309-186.7309-186.7309-186.7309-186.7309Mean-178.7279-179.4437-182.4145-186.7173-182.5721-185.5468Suc.(%d)46.7%40%60%36.7%40%66.7%Time/s1.01310.985471.03993.553717.051431.4902

从表4和图10结果可以得到以下结论:

(1)对第一组单模测试集,MSFL几乎对4个函数都有最好的性能(收敛速度快,成功次数多),其次是vPSO对这组测试函数也有较好的求解结果。另外,从图30中F2 Rosenbrock函数的收敛曲线看出,cPSO的收敛速度是最快的,但是它在成功率上比wPSO vPSO clPSO和MSFL要差;从F3 Ackley的收敛曲线看,wPSO vPSO和MSFL都有不错的全局搜索能力,但是MSFL是收敛速度最快的,成功率最高;F4 Easom测试函数既是单模函数,又含有噪声,wPSO vPSO BasicSFL MSFL都能以较高的成功率求解该函数,但MSFL的收敛速度是最快的。因此,可以明显看出MSFL比其他5类算法在求解单模问题时具有更好的收敛速度和精度。

(2)对第二组多模测试集,从表5中可以看出只有MSFL对3个测试函数均有效。对F5 Rastrigrin和F6 Griewank,其他5种算法几乎都无法求解,这说明它们的保持种群分布能力和收敛速度都比MSFL差;对F7 Schwefel,MSFL和BasicSFL具有很高的求解成功率,而wPSO和vPSO虽然能在30次运算中成功求解该函数,但成功率不高,cPSO和clPSO最多只能得到与标准解接近的结果。因此,可以看出BasicSFL和MSFL比4种PSO算法有更好的全局搜索能力,同时,MSFL在求解多模问题的成功率和收敛速度上是最好的。

(3)对第三组多模-带噪声的测试集,6种算法都能在30次运算中成功求解F8 Levy,但成功率都基本只到50%左右。虽然MSFL的成功率最高,但仍不能达到90%以上。

总之,从三组不同特性的测试函数结果可以看出,MSFL在求解成功率、收敛速度、收敛精度上比其他5种算法好,证明本文改进策略是有效的。但同时也要注意,MSFL的计算时间是最长的,这主要是因为在局部搜索中加入了复杂的最差解更新逻辑。但在实际问题求解中,使用更高性能的计算设备或对实时性要求不高的场合,MSFL具有很高的应用价值。

4.2低维/高维特性对比

上节讨论的8个测试函数结果验证了MSFL在求解单/多模带噪声问题的效率是最高的,但其中的测试函数维数都不高。因此,还需要进一步验证MSFL是否在低维/高维问题中同样有效。以下将8个测试函数中维度可扩展的F1 Sphere、F2 Rosenbrock、F5 Rastrigrin和F6 Griewank四类函数作为本节标准测试函数集,对比wPSO、BasicSFL和MSFL的性能。其中wPSO算法粒子共30个,惯性权重w∈[0,0.9]、C1=C2=2;BasicSFL/MSFL算法中,种群规模30只分为6组,且局部迭代6次。性能评估采用2组实验对比:

(1)固定迭代精度的5维/30维函数性能测试

为了对比测试结果,分别从成功率、最差解、最好解、平均值和平均迭代次数对性能进行对比,每种算法分别用于5维和30维函数性能测试。每组测试运行100次,最大迭代次数为1 000次,统计结果如表5所示。

表5　固定迭代精度的5维/30维函数性能测试结果

分析表5中结果可得以下结论:

(1) 由F1测试结果可知:wPSO和MSFL对低维F1函数都具有很好的性能,可以达到预定的搜索精度(1E-32),且MSFL的成功率和平均值的精度要高于wPSO;当F1测试函数的维数增大到30时,wPSO的求解性能明显下降(成功率为0),而MSFL则无影响,仍然可以100%得到标准解。因此,在简单单模函数求解时,MSFL比wPSO/SFL的鲁棒性好,几乎不受维数约束。

(2) 由F2测试结果可知:求解低维F2时,wPSO和MSFL都有很好的性能;但当维数增大到30维时,wPSO的成功率迅速下降到0,此时MSFL的成功率仍然可以达到100%。对比结果说明,MSFL在求解非凸的病态单模函数时,也几乎不受问题维数的影响。

(3) 由F5/F6测试结果可知,wPSO在低维F5问题求解时,还能在多次运算中求得标准解,但一旦问题维度提高到30维时,成功率又下降为0。而MSFL的成功率始终保持在100%。因此,MSFL在多模问题上的求解性能,也几乎不受问题维度的影响。

(2)固定迭代次数(1 000次)的100维测试函数

第一组测试结果问题维数虽然提高到了30维,可以满足一般工程应用的维度要求,但是对于更加复杂的问题,其求解维度优势会达到更高。因此,还需要分析更高维度下算法的性能,下文采用D=100的4种测试函数 (有效精度范围设置在10-64),每组测试运行10。测试结果以迭代过程中的最优解曲线表示,如图11所示。

图11　D=100测试结果

由图11所示100维求解结果可以看出:MSFL对高维Sphere函数仍然有效,能够在第600次迭代时找到满足收敛精度的解,其他两类

算法均失效;SFL、MSFL、wPSO 3种方法对高维Rosenbrock函数都无能为力,但MSFL在收敛速度和精度上还是优于其他两类算法;MSFL对高维Rastrigrin函数是有效的,只是需要花费更多迭代次数(800次左右)才能找到满足精度的解,其他两类算法均失败;MSFL对高维Griewank函数是有效的,需要大概400次迭代找到满足精度的解,其他两类算法均失败。因此,MSFL在处理更高维复杂问题时仍具有很强的优势,收敛速度和精度比其他2种算法都好。

总之,通过对不同特性标准函数测试集的求解结果对比,以及相同函数低维/高维/更高维时的求解性能对比,验证了本文所提出的MSFL具有很好的全局搜索能力和搜索效率,收敛精度和收敛速度能够在迭代中保持平衡,适用于线性/非线性、单模/多模、低维/高维等多种问题的求解,可以作为本文模型求解器的核心算法。

5　小　结

本文研究了一类新型群体智能算法的收敛性及其改进策略。文中首先分析了基本SFL的计算步骤,从而找到影响算法收敛精度和速度的关键步骤是局部迭代的更新过程。然后,分析了算法收敛性的影响要素:将更新公式变形整理成数列形式,使用等比数列的性质证明了收敛性与系数α和β的取值范围相关;进一步将更新公式整理成系统传递函数形式,使用数字信号处理的稳定性原理分析了不同α和β的取值方法和调节方法对系统阶跃响应稳定性的影响。在此基础上提出一种基于比例系数和适应度标准差的自适应调节策略用于算法改进。最后,使用不同特性的3组共计8种标准测试函数做对比,并对其中4种函数在低维/高维/更高维情况下的测试性能做对比,验证了本文改进策略在改进算法收敛精度和收敛速度的有效性,为复杂问题的求解提供了有效的求解算法支撑。

[1] Eusuff M M, Lansey K E. Optimization of water distribution network design using the shuffled frog leaping algorithm[J].JournalofWaterResourcesPlanningandManagement, 2003, 129(3): 210-225.

[2] Emad E, Tarek H, Donald G. A modified shuffled frog-leaping optimization algorithm: applications to project management[J].StructureandInfrastructureEngineering, 2007, 3(1): 53-60.

[3] Bhattacharjee K K, Sarmah S P. Shuffled frog leaping algorithm and its application to 0/1 knapsack problem[J].AppliedSoftComputing, 2014, 19(19): 252-263.

[4] Luo X H, Yang Y, Li X. Modified shuffled frog-leaping algorithm to solve traveling salesman problem[J].JournalonCommunications, 2009, 30(7):130-135.(罗雪辉,杨烨,李霞. 改进混合蛙跳算法求解旅行商问题[J].通信学报, 2009, 30(7): 130-135.)

[5] Elbeltagi E, Hegazy T, Grierson D. Comparison among five evolutionary-based optimization algorithms[J].AdvancedEngineeringInformatics, 2005, 19(1): 43-53.

[6] Xiao Y Y, Chai X D, Li B H, et al. Convergence analysis of shuffled frog leaping algorithm and its modified algorithm[J].JournalofHuazhongUniversityofScienceandTechnology(NatureScienceEdition),2012,40(7):15-18.(肖莹莹,柴旭东, 李伯虎, 等. 混合蛙跳算法的收敛性分析及其改进[J].华中科技大学学报(自然科学版), 2012, 40(7): 15-18.)

[7] Yang C S, Chuang L Y, Ke C H, et.al. A combination of shuffled frog-leaping algorithm and genetic algorithm for gene selection[J].JournalofAdvancedComputationalIntelligenceandIntelligentInformatics, 2008, 12(3): 218-226.

[8] Zhang X, Hu X, Cui G, et al. An improved shuffled frog leaping algorithm with cognitive behavior[C]∥Proc.ofthe7thIEEEWorldCongressonIntelligentControlandAutomation, 2008: 6197-6202.

[9] Zhen Z, Wang D, Liu Y. Improved shuffled frog leaping algorithm for continuous optimization problem[C]∥Proc.oftheIEEECongressonEvolutionaryComputation, 2009: 2992-2995.

[10] Huynh T H. A modified shuffled frog leaping algorithm for optimal tuning of multivariable PID controllers[C]∥Proc.oftheIEEEInternationalConferenceonIndustrialTechnology, 2008: 1-6.

[11] Ping D A, Fang W H. Adaptive particle swarm optimization algorithm with dynamically changing inertia weight[J].Control&Decision, 2008, 23(11): 1253-1257.

[12] Chen W N, Zhang J, Lin Y, et al. Particle swarm optimization with an aging leader and challengers[J].IEEETrans.onEvolutionaryComputation, 2013, 17(2): 241-258.

[13] Mehrabian A R, Lucas C. A novel numerical optimization algorithm inspired from weed colonization[J].EcologicalInformatics, 2006, 1(4): 355-366

[14] Hao G, Hao L W, Bo X W. A global convergence algorithm of particle swarm optimization and its convergence analysis[J].Control&Decision, 2009, 24(2): 196-201.

[15] Shi Y, Eberhart R. A modified particle swarm optimizer[C]∥Proc.oftheIEEEInternationalConferenceonEvolutionaryComputation, 1998: 69-73.

[16] Clerc M, Kennedy J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J].IEEETrans.onEvolutionaryComputation, 2002, 6(1): 58-73.

[17] Pehlivanoglu Y V. A new particle swarm optimization method enhanced with a periodic mutation strategy and neural networks[J].IEEETrans.onEvolutionaryComputation,2013,17(3):436-452.

[18] Liang J J, Qin A K, Suganthan P N, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEETrans.onEvolutionaryComputation, 2006, 10(3): 281-295.

Improvement strategy of adaptive parameter adjustment for shuffled frog leaping algorithm

XIAO Ying-ying1,2, LIN Ting-yu1,2, LI Bo-hu2,3, HOU Bao-cun1,2,3, SHI Guo-qiang1,2,3

(1. Beijing Complex Product Advanced Manufacturing Engineering Research Center, Beijing Simulation Center, Beijing 100854; 2. State Key Laboratory of Intelligent Manufacturing System Technology,Beijing Institute of Electronic System Engineering, Beijing 100854; 3. Science and Technology on Space System Simulation Laboratory, Beijing Simulation Center, Beijing 100854)

An improvement strategy of adaptive parameter adjustment is proposed to improve the efficiency of the shuffled frog leaping algorithm (SFL) in solving high dimensional complex problems. First of all, the convergence feature of the SFL is analyzed based on the theory of geometrical sequence. Then, an improvement strategy of adaptive parameter adjustment based on proportional coefficient and fitness standard deviation is proposed to the update the formula. Finally, based on three groups of eight criteria functions, the performance of the modified SFL with basic SFL and four modified particle swarm optimization (PSO) is compared, and the results verify the high-efficiency of the improvement strategy for various complex functions. Meanwhile, the performance of the modified SFL with basic SFL and wPSO on solving high dimension problems is compared, and the results verify the validity of the modified SFL.

shuffled frog leaping (SFL) algorithm; convergence feature; adaptive parameter adjustment; intelligent computing

2016-02-22；

2016-03-28；网络优先出版日期：2016-06-19。

国家高技术研究发展计划(863计划)(2015AA042101)资助课题

TP 391

10.3969/j.issn.1001-506X.2016.08.34

肖莹莹(1987-),女,博士研究生,主要研究方向为智能制造、智能优化算法。

E-mail: xiaoyingying504@126.com

林廷宇(1984-),男,博士,主要研究方向为智能制造、云制造、网络化建模与仿真系统。

E-mail:lintingyu2003@sina.com

李伯虎(1938-),男,中国工程院院士,博士研究生导师,主要研究方向为网络化建模与仿真系统、虚拟样机工程、网格化、智能化、服务化制造系统。

E-mail: bohuli@moon.bjnet.edu.cn