基于压缩感知的高动态范围混合信号采样方法研究

罗浚溢 刘涛

摘 要：为能够有效获取高动态范围混合信号的弱信号，提出一种基于压缩感知的信号采样方法。通过弱信号与预估值之间的最小均方差得到一种新的感知矩阵，该感知矩阵可以在抑制强信号的同时保留弱信号；利用相干分析法验证该矩阵满足约束等距性条件，并对噪声误差进行分析。实验结果表明：该方法可实现高动态范围混合信号的弱信号的采样与重构。

关键词：压缩感知；混合信号；高动态范围；最小均方差

文献标志码：A 文章编号：1674-5124（2016）09-0112-04

0 引 言

高动态范围的混合信号可以被视为由高幅值（即强信号）和低幅值（即弱信号）组成。对这类信号进行分析的过程中有效地获取到弱信号，主要挑战在于在对混合信号的采样过程中避免由于量化值过高造成的弱信号不可逆的损失。

在工程上的传统做法是使用ACG等器件适当放大输入信号满足ADC最优的转换范围[1]。这种方法的缺点是由于强信号与弱信号在时域中是混合的，在放大弱信号的同时强信号也会被放大，当强信号放大的幅值超过允许的输入范围时，ADC将无法正常工作。

有效采样弱信号的另一种方法是抑制强信号效应。对高动态混合稀疏或可压缩信号而言，压缩感知（CS）[2]技术提供了一种很好的方法。由于基于压缩感知的信号采集和处理机制对噪聲和外部干扰非常敏感，为了能够确保弱信号重构的准确度，必须首先抑制强信号的效应[3]。文献[4]提出了基于正交投影的感知矩阵生成方法，文献[5]提出一种基于斜投影的感知矩阵生成方法。这两种方法都可以有效抑制强信号的干扰，但是并没有考虑噪声信号对弱信号的影响。

本文提出一种新的感知矩阵的生成方法，这种矩阵可以在噪声和外部干扰的条件下有效地实现对弱信号的采样。

4.4 重构信噪比实验与分析

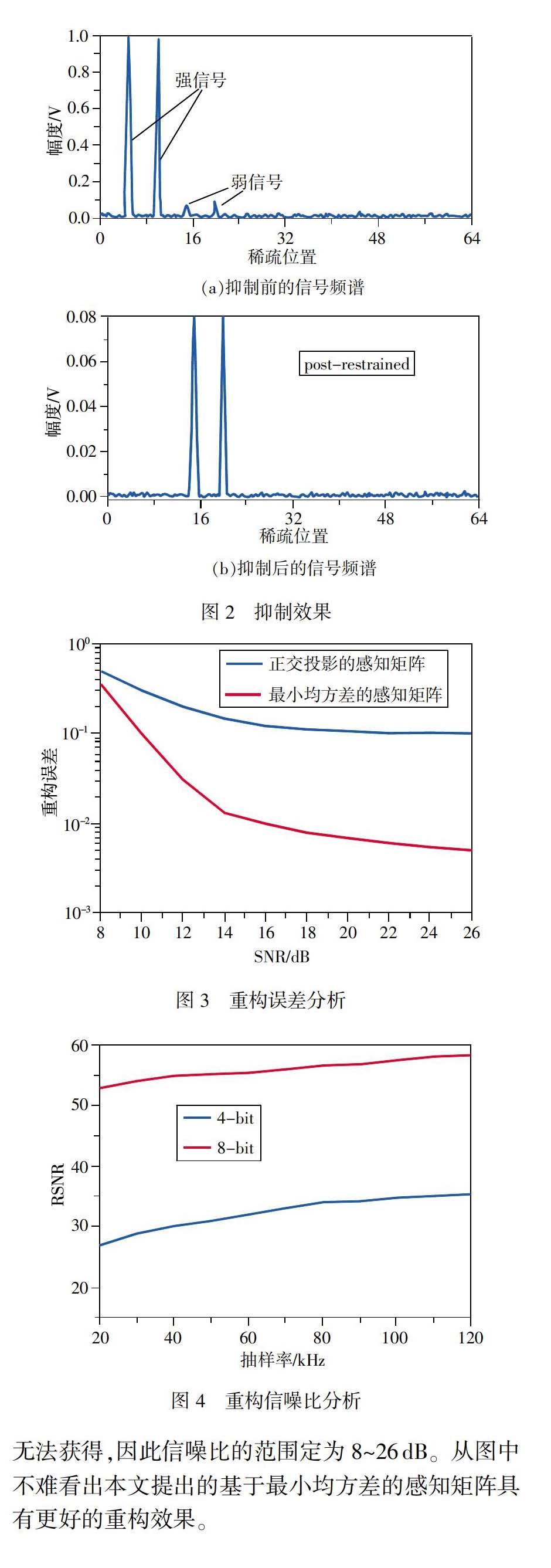
为能够更好地说明本文提出的感知矩阵获取方法的有效性，需要对新系统的重构信噪比进行分析。如图4，输入信号为0.5 MHz（弱信号）和1 MHz（强信号）的正弦混合信号，动态范围为100 dB。现分别选取分辨率为4-bit和8-bit的ADC对信号进行采样。从图中可以看出，在采样率为20 kHz时，4-bit和8-bit对应的信噪比为27 dB和53 dB，都优于传统的香农采样方法。

5 结束语

本文重点研究了高动态范围的混合信号采样方法。提出了一种新的方法来抑制强信号并保留弱信号。该方法在考虑噪声影响的条件下，以重构后的弱信号和估计值之间的最小均方误差（MSE）得出感知矩阵。对比实验表明，本文所提出的方法的有效性和优越性。

参考文献

[1] DENNIS R. MGRGAN. A/D conversion using geometric feedback AGC[J]. IEEE Trans. On Computer，1975，24（11）：1074-1078.

[2] DONOHO D. Compressed sensing[J]. IEEE Trans Inform Theory，2006（52）：1289-1306.

[3] MARK A， PETROS T. Signal processing with compressive measurements[J]. IEEE Journal of Selected Topics in Signal Processing，2010，4（2）：445-460.

[4] DAVENPORT M， BOUFOUNOS P， BARANIUK R. Compressive domain interference cancellation. Proceedings of the workshop： signal processing with adaptive sparse structured representations（SPARS）[J]. Saint-Malo：Interna

tional Center for Mathematical Sciences，2009（3）：1-5.

[5] 田鹏武，康荣宗，于宏毅. 基于斜投影算子的压缩域滤波法[J]. 北京邮电大学学报，2012，35（3）：108-111.

[6] CANDES E， WAKIN M. An introduction to compressive sampling[J]. IEEE Sigproc Mag，2006，52（2）：21-30.

[7] CAND E J， ROMBERG S J， Tao T. Robust uncertainty principles： Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transaction on Information Theory，2006，52（2）：489-509.

[8] EMMANUEL J C. The restricted isometry property and its implications for compressed sensing[J]. C. R. Math. Acad. Sci. Paris，2008，346（9-10）：589-592.

[9] RICHARD B， MARK D， RONALD D， et al. A simple proof of the restricted isometry property for random matrices[J]. Constructive Approximation，2008，28（3）：253-263.

[10] 罗浚溢，田书林，刘涛. 最小L1范数实现周期非均匀采样与重构研究[J]. 电子科技大学学报，2012，5（3）：418-423.

（编辑：刘杨）