改进的物元分析法在水质监测断面布设优化中的应用
2016-08-13蒋艳君谢悦波
蒋艳君,谢悦波,黄 旻
(1.河海大学水文水资源学院,江苏 南京 210098; 2.金华市浦江县环境监测站,浙江 金华 322200)
改进的物元分析法在水质监测断面布设优化中的应用
蒋艳君1,谢悦波1,黄旻2
(1.河海大学水文水资源学院,江苏 南京210098; 2.金华市浦江县环境监测站,浙江 金华322200)
摘要:依据传统物元分析法的原理,使用层次分析法结合熵权法的组合权重法对物元分析法的权重计算进行改进,对关联度进行聚类分析,使传统的物元分析法得到改进与拓展。以浦阳江干流9个水质监测断面,主要监测指标CODMn、COD、TP、NH3-N及氟化物的2012年监测数据为基础,采用改进的物元分析法对水质监测断面进行优化,将原有9个断面优化为7个断面,并对优化结果进行一致性检验,结果显示,改进的物元分析法优化结果准确、有效。
关键词:层次分析法;熵权法;组合权重法;断面优化;改进的物元分析法;聚类分析
水质监测断面的布设方案直接影响水质监测结果,断面优化布设体现监测工作的科学性、合理性,水质监测断面布设的总原则为以最少的断面、测点数,取得最全面、科学、合理的水质监测信息[1]。传统的水质监测断面常依据水资源保护管理的需要以及相关条例的规定而布设[2],具有较强的主观性,并不能完全符合水质监测断面布设的总原则。可利用数理统计的方法对水质监测断面布设进行优化,常用的数理统计方法有物元分析法[3-4]、历史数据相关分析法[5]、模糊聚类分析法[6]、人工神经网络模型[7]等。
物元分析法能有效地解决多项水质指标优选监测断面存在的不相容问题[8],笔者将层次分析法与熵权法结合,对物元分析法的权重计算进行改进,对关联度进行聚类分析,提出利用改进的物元分析法对水质监测断面布设进行优化。
1 改进的物元分析法
基于监测断面多项水质监测指标的监测值和将其标准化处理后得到的标准值,利用物元分析法建立系列物元矩阵进行对比分析,计算多项指标的综合关联函数,分析其关联度,划分断面的亲近关系。
1.1构造物元矩阵和节域物元矩阵
根据各监测断面指标监测数据,计算各项监测指标的平均值,构造平均值矩阵C,对于值越大表示水质越差的指标,分别取其平均值的最小值和最大值,构成最优值矩阵A和最劣值矩阵B;对于值越小表示水质越差的指标,分别取其平均值的最小值和最大值的倒数,构成相应矩阵。监测指标的平均值、最优值、最劣值构成的标准物元矩阵[8]表达式为
式中:RAC为最优值标准物元矩阵;RCB为最劣值标准物元矩阵;MAC、MCB为标准事物;n为监测指标数;Qj为各项监测指标;aj、bj、cj分别为各项监测指标年均值的最小值、最大值、平均值。
由监测指标的最大值与最小值构成的节域物元矩阵为
(3)
再将每一个采样点的水质监测数据作为一个物元,构成物元矩阵
(4)
式中:RAB为节域物元矩阵;Ri为物元矩阵;Mi为对象;xij为第i个监测断面各监测指标的平均值。
1.2改进权重计算
笔者将计算主观权重的层次分析法与计算客观权重的熵权法结合,构成组合权重法对物元分析法的权重计算进行改进,组合权重法能很好地表达监测指标对优选结果的作用,同时反映出各监测指标之间的相互作用,形成互补,使权重系数更具合理性。
1.2.1层次分析法
根据水质监测指标与地表水环境质量标准的5级水质类别[9],构建水质的递阶层次结构[10],见图1。
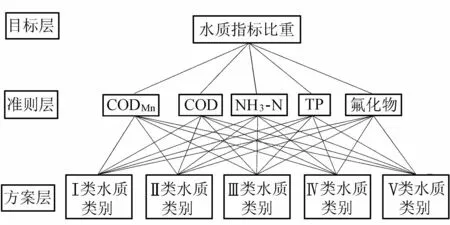
图1 层次分析法结构
层次分析法步骤[11]如下:
a. 筛选水质监测指标。笔者选取CODMn、COD、TP、NH3-N及氟化物作为主要监测指标。
b. 构造判断矩阵。以各准则层相对重要度构建判断矩阵D=(dij)n×n,见表1,Bk为准则层中的指标准则(k=1,2,…,5),dCODMn、dCOD、dNH3-N、dTP、dF分别为CODMn、COD、TP、NH3-N及氟化物的监测值。
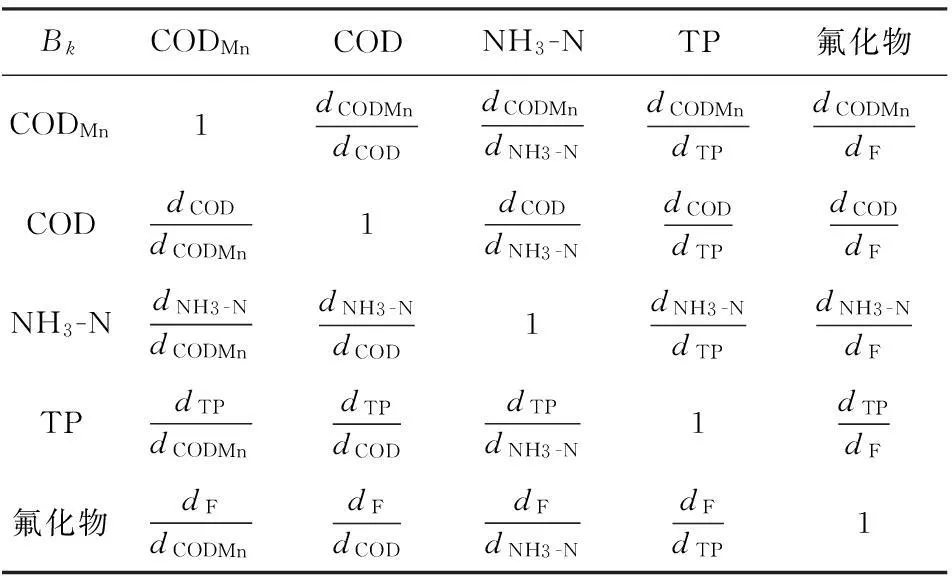
表1 判断矩阵
c. 求解最大特征值。采用特征向量法,使用Matlab软件编程,对判断矩阵的最大特征值λmax进行求解。
d. 一致性检验。采用判断矩阵D除去最大特征值λmax的其他特征值的负均值,作为衡量判断矩阵是否一致的数值指标,即一致性检验指标CI:
(5)
其中,CI值越小,表示一致性越好;反之越差。
1.2.2熵权法
熵权法具体步骤[12]如下:

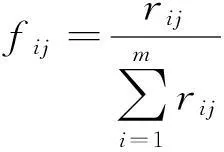
c. 信息熵值计算。第j个监测指标的信息熵值计算表达式为
(6)
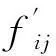
(7)
d. 熵权计算。熵权计算表达式为
(8)
熵权向量为ω2=(ω21,ω22,…,ω2j,…,ω2n),其中ω2j为权重向量的分量。
1.2.3组合权重
笔者将层次分析法与熵权法结合,构成组合权重法对物元分析法赋权,计算式[13]为
(9)
式中:ω1i、ω2i分别是层次分析法与熵权法计算得到的权重向量的分量,i=1,2,…,5。
1.3关联函数
关联函数K(xij)用来描述监测断面物元与标准物元的符合程度[14],其含义为:①当K(xij)≥0时,表示比较对象符合标准对象要求,其值越大,符合程度越高;②当-1≤K(xij)<0时,表示比较对象不符合标准对象要求,但具备转化为标准对象的条件,其绝对值越大,越容易转化;③当K(xij)<-1时,表示比较对象不符合标准对象要求,且不具备转化为标准对象的条件。
分别建立每一监测断面各项监测指标对A、B的线性关联函数[15]:
(10)
(11)
所有监测指标对A、B的综合关联函数为
(12)
(13)
式中:KA(xij)、KB(xij)分别为第i个监测断面第j个监测指标对A、B的线性关联函数;KA(xi)、KB(xi)分别为第i个监测断面对A、B的综合关联函数;xij为断面各项指标的监测值;aj、bj、cj分别为监测指标年均值的最小值、最大值与平均值;ωj为各监测指标的权重系数;xi为第i个监测断面监测指标的最小值和最大值的平均值。以最优、最劣综合关联函数值为基础,采用SPSS软件实现系统聚类分析过程[16]。
2 实例应用
2.1研究区域简介
以浦阳江干流9个水质监测断面,2012年主要监测指标CODMn、COD、TP、NH3-N及氟化物的年均值数据为基础,上游至下游监测断面依次编号1~9号,位置见图2。应用改进的物元分析法对9个断面进行优化分析,主要监测指标的质量浓度年均值见表2。
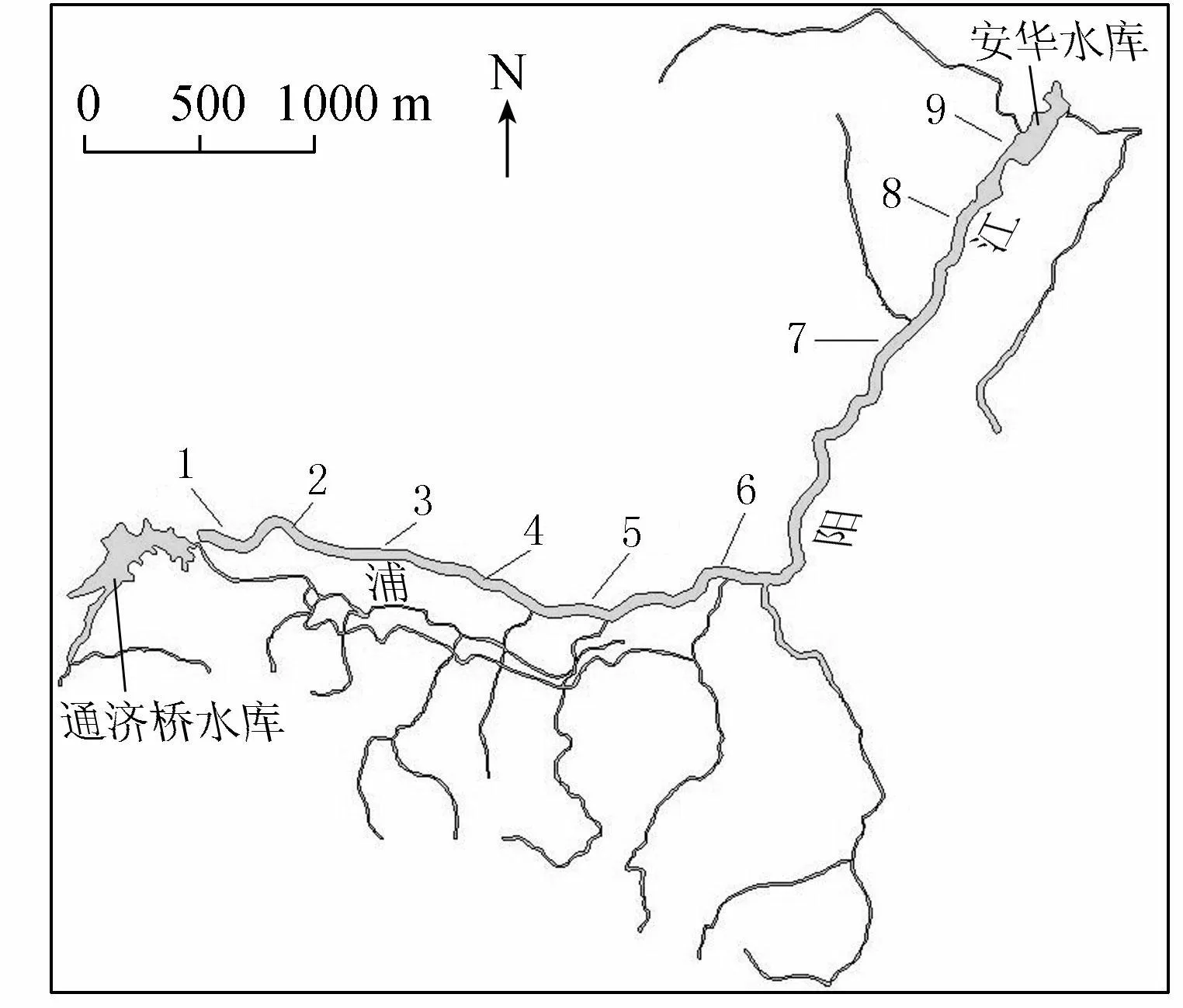
图2 浦阳江水系及断面位置分布
2.2物元矩阵及权重确定
根据式(1)~(2),计算所得标准物元矩阵及节域物元矩阵如下,Q1为CODMn;Q2为COD;Q3为TP;Q4为NH3-N;Q5为氟化物。
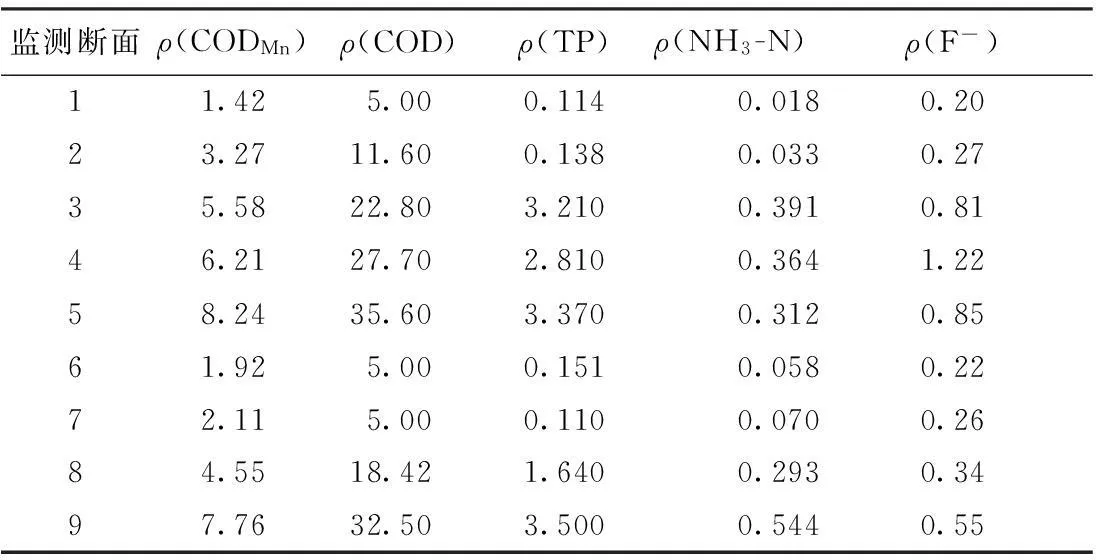
(14)
(15)
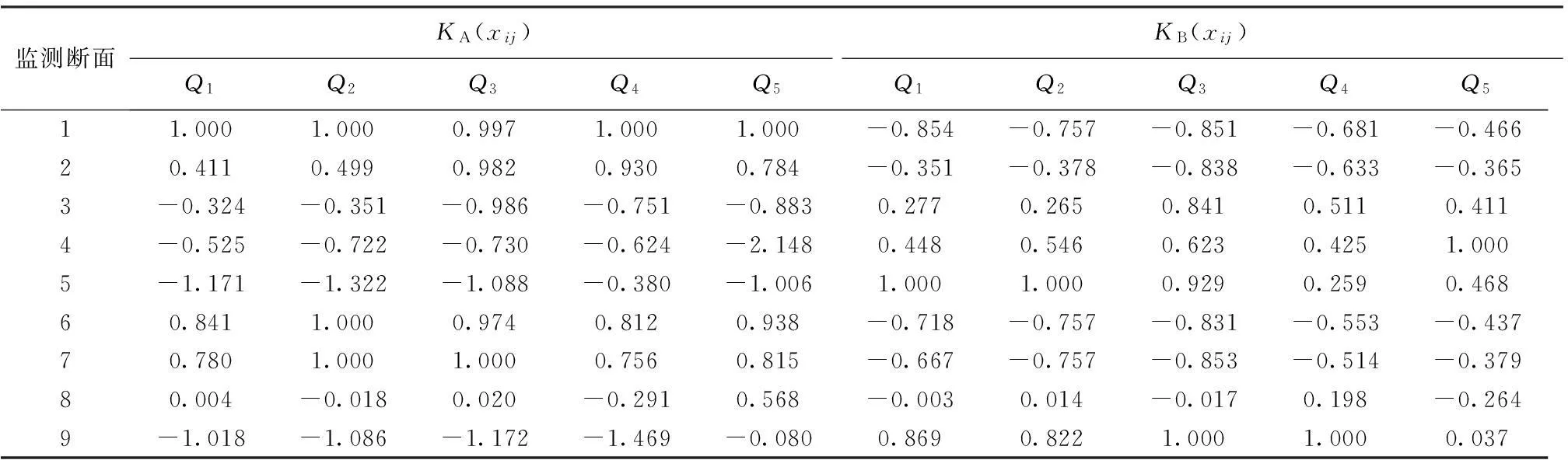
(16)
根据式(16)计算得到9个监测断面的物元矩阵Ri(i=1,2,…,9),给出1号断面的物元矩阵R1作为示例:
(17)
运用层次分析法及熵权法计算所得权重结果分别为:ω1=(0.202,0.717,0.049,0.008,0.024),ω2=(0.232,0.252,0.134,0.204,0.181)。组合权重为:ω=(0.261,0.513,0.098,0.049,0.079)。
2.3关联函数值确定及聚类分析
根据式(14)~(15)计算9个断面的线性关联函数结果,见表3。
根据式(6)~(7),计算最优、最劣综合关联函数,结果见表4。
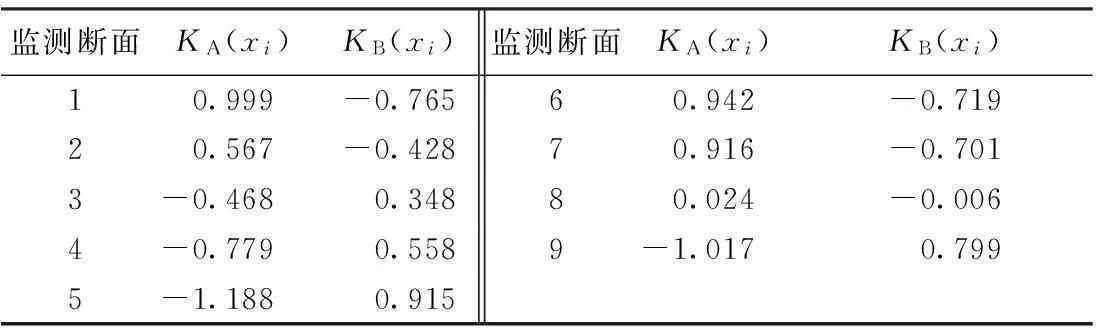
表4 最优、最劣综合关联函数值
以最优综合关联函数KA为纵坐标,以最劣综合关联函数KB为横坐标,绘制每个监测断面关联函数点聚图,见图3。

图3 最优、最劣综合关联函数点聚图
将每个监测断面的最优、最劣综合关联函数值作为监测断面系统聚类分析的基础数据,使用SPSS软件对各监测断面进行系统聚类分析,结果见图4。
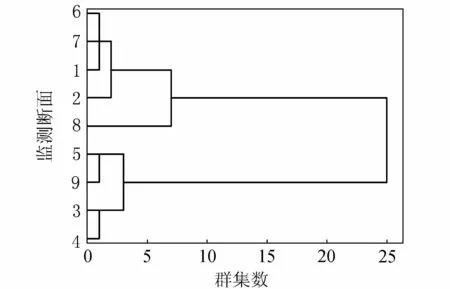
图4 系统聚类分析树状图
根据水质监测断面的实际位置及检测功能作用,本实例将9个水质监测断面分为3大类,聚类优化结果见表5。
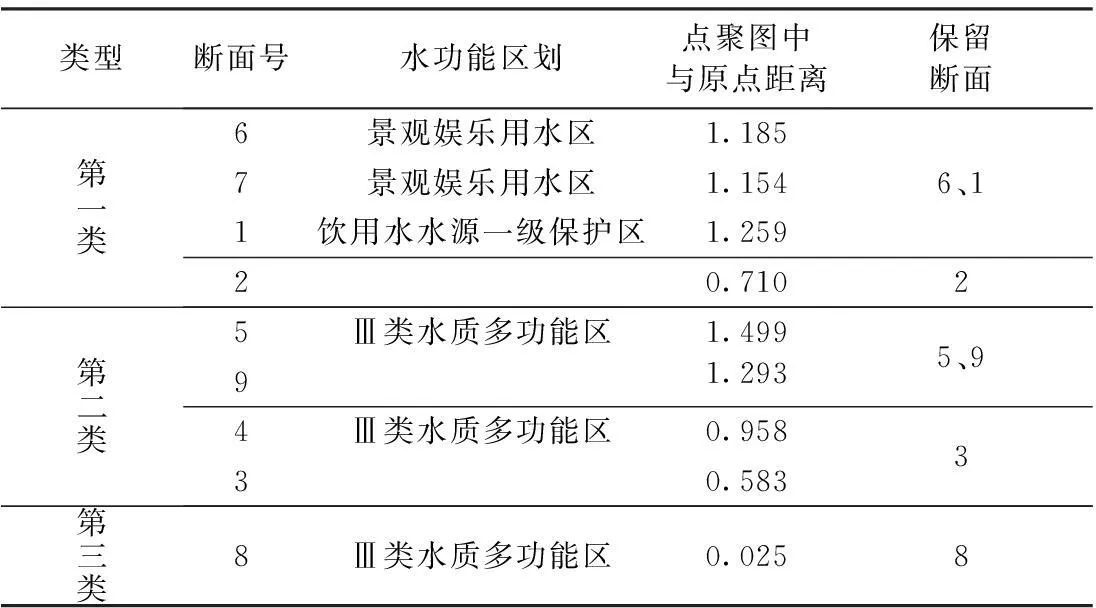
表5 聚类优化结果
对于第一类的4个监测断面6、7、1、2,根据断面实际地理位置及监测功能分析,6、7号监测断面相距较近且监测功能一致,1号监测断面位于流域入口且为监测饮用水水源地之用,2号监测断面与6、7号监测断面相距较远,故保留6、1、2号监测断面;对于第二类的4个监测断面5、9、4、3,5、4号监测断面相距较近检测功能一致,9号监测断面位于支流与干流汇流处,故保留5、9号监测断面,3号断面监测功能与5、9号断面不同,故作为保留;第三类的8号断面作为保留。
将优化前水质监测数据与优化后水质监测数据作为两个样本,采用F检验与t检验对两个样本的均值做一致性检验,检验结果见表6。
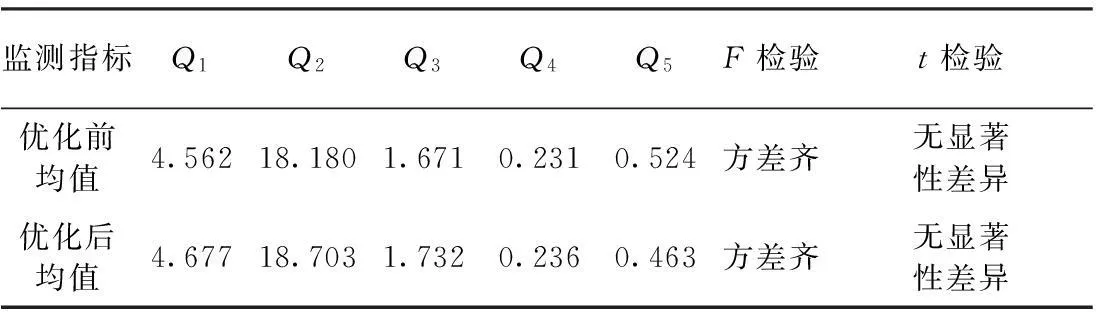
表6 优化前后断面水质监测数据及相关性检验结果
综上所述,通过改进的物元分析法对浦江县9个水质监测断面进行优化分析,将9个监测断面最终优化为7个监测断面1、2、3、5、6、8、9,删减2个监测断面节约了资源与成本,实现断面优化布设的科学性。
3 结 语
笔者对传统物元分析法的权重计算方法及关联函数方面进行了改进,使传统物元分析法得到拓展与改进,分析结果更为科学合理,适用于各种监测断面的优化选择。利用改进的物元分析法对浦江县9个水质监测断面进行优化选择,结合主观权重与客观权重对各个断面主要监测指标进行赋权,使权重计算更为科学合理,使用SPSS软件对综合关联函数值进行聚类分析,相比目测聚类更为科学。得到的优化结果通过了一致性检验,改进的物元分析法为水质监测断面优化提供了一种科学、实用、有效的方法。
参考文献:
[1] 谢悦波.水信息技术[M].北京:中国水利水电出版社,2009.
[2] 樊引琴,李婳,刘婷婷,等.物元分析法在水质监测断面优化中的应用[J].人民黄河,2012,34(11):82-84.(FAN Yinqin,LI Hua,LIU Tingting,et al.Application of matter element analysis method in optimized sections of water quality monitoring[J].Yellow River,2012,34(11):82-84.(in Chinese))
[3] 蔡文.物元分析[M].广州:广东高等教育出版社,1987.
[4] 朱慧君,于永斌.物元分析法在大气监测优化布点中的应用[J].云南环境科学,1987,17(4):51-53.(ZHU Huijun,YU Yongbin.Application of matter element analysis to optimized sites of atmospheric monitoring[J].Yunnan Environmental Science,1987,17(4):51-53.(in Chinese))
[5] 赵吉国.东江流域地表水监测省控断面优化布点[J].广东水利水电,2004(6):27-29.(ZHAO Jiguo.Optimization of province controlled surface water monitoring section in the Dongjiang distribution[J].Guangdong Water Resources and Hydropower,2004(6):27-29.(in Chinese))
[6] 王晶,孙世群,邵超,等.模糊聚类分析法在水质监测断面优化中的应用[J].广州化工,2012,40(7):153-154,160.(WANG Jing,SUN Shiqun,SHAO Chao,et al.Fuzzy cluster analysis in the optimization of water quality monitoring sections[J].Guangdong Chemical Industry.2012,40(7):153-154,160.(in Chinese))
[7] 何璠.基于BP人工神经网络的环境质量评价模型研究[D].成都:四川大学,2006.
[8] 曹毅.物元分析法在水质监测优化布点中的应用[J].环境监控与预警,2012,4(1):43-45,52.(CAO Yi.Application of metter-element analysis in optimized points selection of water quality monitoring[J].Environmental Monitoring and Forewarning,2012,4(1):43-45,52.(in Chinese))
[9] 中华人民共和国国家环境保护总局.GB3838—2002地表环境质量标准[S].北京: 中国环境科学出版社,2002.
[10] 邓雪,李家铭,曾浩健,等.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识,2012,42(7): 93-100.(DENG Xue,LI Jiaming,ZENG Haojian,et al.Research on computation methods of AHP wight vector and its applications[J].Mathematics in Practice and Theory,2012,42(7): 93-100.(in Chinese))
[11] 卢文喜,李迪,张蕾,等.基于层次分析法的模糊综合评价在水质评价中的应用[J].节水灌溉,2011(3):43-46.(LU Wenxi,LI Di,ZHANG Lei,et al.Application of fuzzy comprehensive evaluation based on AHP in water quality evaluation[J].Water Saving and Irrigation,2011(3):43-46.(in Chinese))
[12] 冯斌.模糊综合评价的熵权法在地下水水质评价中的应用[J].中国水运,2012,12(7): 186-187.(FENG Bin.Fuzzy comprehensive evaluation of entropy method in groundwater quality evaluation[J].China Water Transport,2012,12(7): 186-187.(in Chinese))
[13] 乔雨,梁秀娟,王宇博,等.组合权重模糊数学法在水质评价中的应用[J].人民黄河,2015,37(5):77-79.(QIAO Yu,LIANG Xiujuan,WANG Yubo,et al.Evaluation of groundwater quality using combined weight fuzzy mathematical method[J].Yellow River,2015,37(5):77-79.(in Chinese))
[14] 孙学颖,唐德善,张新娇.改进物元分析模型在北之江流域水质评价中的应用[J].南水北调与水利科技,2014,12(3):55-58.(SUN Xueying,TANG Deshan,ZHANG Xinjiao.Application of improved metter-element model in water quality assessment of Beizhijiang Drainage Basin[J],South-to-North Water Transfers and Water Science & Technology,2014,12(3):55-58.(in Chinese))
[15] 马飞,蒋莉.河流水质监测断面优化设置研究: 以南运河为例[J].环境科学与管理,2006,31(8):171-172.(MA Fei,JIANG Li.Research of optimized setting of water quality monitoring sections in rivers: take South Canal as an example[J].Environmental Science and Management,2006,31(8):171-172.(in Chinese))
[16] 杨静.改进的模糊综合评价法在水质评价中的应用[D].重庆:重庆大学,2014.
DOI:10.3880/j.issn.1004-6933.2016.04.023
作者简介:蒋艳君(1992—),女,硕士研究生,研究方向为水生态修复。E-mail:640483090@qq.com 通信作者:谢悦波,教授。E-mail:xyb@hhu.edu.cn
中图分类号:TV213.4;X832
文献标志码:A
文章编号:1004-6933(2016)04-0136-06
(收稿日期:2015-09-13编辑:王芳)
Application of improved matter element analysis method to optimization of water quality monitoring sections
JIANG Yanjun1, XIE Yuebo1, Huang Min2
(1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China;2.EnvironmentalMonitoringStationofPujiangCounty,JinhuaCity,Jinhua322200,China)
Abstract:According to the principles of traditional matter element analysis methods, the combined weight method, which is the combination of the AHP method and the entropy method, was used to modify the weights in the matter element analysis method. Then, the relevance was studied through cluster analysis, and thus the traditional matter element analysis method was improved and expanded. Based on monitoring data involving CODMn, COD, TP, NH3-N, and fluoride, at nine water quality monitoring sections on the main stream of the Puyang River in 2012, the improved matter element analysis method was used to optimize these water quality monitoring sections. As a result, the original nine sections were decreased to seven sections after optimization. The results were verified by the consistency test, indicating that the improved matter element analysis method can provide accurate and effective optimization results.
Key words:AHP; entropy method; combined weight method; section optimization; improved matter element analysis method; cluster analysis
