空间索形悬索桥吊装施工过程分析方法

王晓明， 贺耀北， 陈　多

(1. 长安大学 桥梁工程研究所, 陕西 西安 710064； 2. 长安大学 旧桥检测与加固技术交通行业重点实验室, 陕西 西安 710064；3. 湖南省交通规划勘察设计院, 湖南 长沙 410008； 4. 上海市政工程设计研究总院(集团)有限公司， 上海 200092)



空间索形悬索桥吊装施工过程分析方法

王晓明1,2， 贺耀北3， 陈多4

(1. 长安大学 桥梁工程研究所, 陕西 西安 710064； 2. 长安大学 旧桥检测与加固技术交通行业重点实验室, 陕西 西安 710064；3. 湖南省交通规划勘察设计院, 湖南 长沙 410008； 4. 上海市政工程设计研究总院(集团)有限公司， 上海 200092)

摘要：以主缆与吊索的下料长度、索夹安装位置为联系，构建吊索下端力矩阵，并建立各个施工阶段临时体系相互独立的平衡方程.分别采用考虑重力的多段二力杆、分段三维悬链线来分析空间索的双向垂度特征，并提出了2种主梁吊装过程的解析解.利用数值迭代法，实现不依赖于前行施工阶段，独立求解任一工况的物理状态.算例分析表明，该方法对施工状态的实时变动能迅速作出响应，适合施工过程的实时监控与技术决策分析.

关键词：悬索桥; 空间索形; 施工过程; 二力杆; 分段空间悬链线

空间索形悬索桥不仅造型优美，而且同时存在竖向与横向垂度，其主缆和吊索形成一个三维的索系.从静力上讲，这种体系在对竖向承载能力影响不大的情况下，缆索系统的横向承载能力得到显著提高；从动力上讲,横桥向倾斜的吊杆与加劲梁构成一个稳定的三角形，每对斜吊杆中的横桥向水平分力将加劲梁夹住，使得主梁有类似钟摆的回复力，提高了整体扭转刚度.这种缆索体系的改变可以有效抵抗桥梁的气动失稳[1].

目前国内外的空间索形悬索桥都属于自锚式体系，由于主缆需要锚固在梁上后才能承重，故绝大多数采用“先梁后缆”吊索张拉施工，典型的有韩国的永宗大桥[2-3]、美国的奥克兰海湾新桥、天津的富民桥、广州的猎德大桥和杭州江东大桥.为了克服这种“先梁后缆”施工对下穿航道或路面交通的影响，同时避免传统临时地锚法[4]对地基、地形及投资的高要求，通过改进施工工艺[5]，“先缆后梁”吊装施工已经成功应用于大跨径空间索形自锚式悬索体系——东苕溪大桥(75 m+228 m+75 m)[6]，改进后的“先缆后梁”吊装施工法经济、社会效应明显，能够有效推动此类桥型的广泛应用.

对于空间索形悬索桥，已有文献主要集中于成桥状态分析方法和“先梁后缆”吊索张拉过程分析方法的研究.成桥状态分析方面，文献[7]为初始平衡状态建立了主缆、吊索相互耦合的空间解析模型，提出了一种高效的空间缆索耦合体系分析方法.文献[8]针对空间索形自锚式悬索桥的空间缆索系统耦合特性及自锚式的自平衡特性，提出了该体系初始平衡状态的2种解析解.文献[9]直接从三维索的几何方程和平衡方程出发，将三维主缆投影到2个平面上，分别考虑几何边界条件和力的平衡条件以及倾斜吊杆的影响，引入梯度迭代法，推导了三维主缆的迭代方程.文献[10]采用空间分析模型,提出了空间主缆悬索桥成桥状态和空缆状态主缆线形分析的数值计算方法.文献[11]推导了主缆找形目标变量变化值与迭代变量变化值之间的关系，从而为空间主缆自锚式悬索桥建立了确定成桥状态的高效方法.吊索张拉过程分析方面，文献[12]介绍了一套模拟平面索形自锚式悬索桥施工的精细迭代算法，该算法将施工过程仅分为2个施工阶段(全部自重阶段和二期恒载阶段)来处理.文献[13]给出了调整吊索无应力长度的降温法，在有限元程序中模拟自锚式悬索桥体系转换过程中吊索张拉力及张拉程序.文献[14]依据桃花峪大桥1∶30的缩尺模型试验结果，研究了自锚式悬索桥张拉施工过程中的力学行为，分析出边、中跨主缆不同的非线性效应和变形规律及吊索索力随施工过程的变化规律.

关于空间索形自锚式悬索桥“先缆后梁”吊装施工过程的分析研究，工程上主要采用有限元程序计算[15]，尚未见专门的分析方法报道.采用有限元程序分析空间索形悬索桥的吊装施工过程，存在以下不足：① 收敛耗时长.除了存在传统平面索形悬索桥吊装过程中的大变形问题，空间索形悬索桥的吊索是横桥向倾斜的，会产生随施工过程变化的横桥向分力，故分析过程非线性更强，对有限元分析程序的收敛能力要求非常高，每个工况耗时很长.② 依赖先行工况，分析时效性较差.有限元的正装分析依赖于上一个施工阶段的内力和线形状态，通过继承前行阶段的效应状态，利用叠加作用变化量引起的效应增量，来确定当前阶段的平衡，如果当前阶段的作用发生变化，为了得到实时效应结果，需要全部从头重新分析一遍，非常费时.因此，虽然便于预测前面工况对后续工况的影响，但不便于反映当前工况施工状态的动态变化，难以适用于施工阶段多且需要实时分析的复杂工程.

实际工程中，施工过程的方案调整与工况变化时有发生，作为技术决策直接支撑的模型分析，在监控过程需要反复地主动或被动调整，时间紧迫.由于上述不足引起的时效性低下，往往导致影响因素作用规律分析不足，技术决策思路不连贯，对于紧急情况常常出现模型分析滞后于工程需求.

本文从施工过程临时体系的力学平衡角度入手，为吊装各个阶段建立平衡条件的递推式，结合边界条件求解吊装各个阶段的几何、内力状态.各个吊装工况通过主缆、吊索下料长度及索夹安装位置相互联系，各自的力学平衡方程相互独立，求解可单独进行，无需继承上一阶段的效应状态.

1　分析假定

在吊装施工过程中，各个施工阶段形成的临时体系都能达到相互独立的力学平衡状态，各阶段之间相互联系的纽带是：主缆与吊索的下料长度及索夹安装位置保持不变.

本文以主缆、吊索的下料长度为联系，建立各个施工阶段相互独立的力学平衡方程，通过构建吊索下端力矩阵对其依次求解，从而实现施工阶段的全过程解析分析.其中，每一列对应一个吊装工况，可以独立求解任意工况的物理状态，无需依赖于前行施工阶段.

根据制定的吊装顺序，构建如式(1)所示的吊杆下端竖向力矩阵Py.每一列对应一个吊装工况，分别采用本文算法，即可确定此工况下的几何、力学参数.

(1)

(2)

其中，wi为吊索i对应梁段的恒载重力.

2　吊装阶段平衡状态的二力杆解

根据吊装施工过程，作如下假定：

(1) 吊装过程中吊索仅沿横桥向倾斜，忽略该过程可能存在的吊索顺桥向的微小倾斜.

(2) 主缆缆段、吊索简化为考虑自重的二力杆.

在上述假定下，存在如下基本定理：

(1) 主缆吊点的顺桥向坐标x、竖向坐标y，以及主缆吊点的顺桥向水平力、竖向力不受横桥向力的影响.

(2) 主缆吊点的横桥向坐标z，以及主缆吊点的横桥向水平力不受竖向力的影响.

(3) 吊杆竖向力只引起主缆在竖直平面内的伸长,横向力只引起主缆在水平面内的伸长.

因此，采用二力杆模拟时，竖直投影面与水平投影面是可以解耦独立求解的.

2.1竖直投影面

如图1所示，以吊点为研究对象，可建立如下力的平衡方程:

(3)

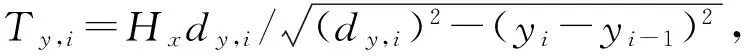
图1　主缆竖直投影面计算图式

(4)

当i=1～(n+1)/2时取加号，当i=(n+3)/2～n时取减号.

主缆吊点的顺桥向坐标xi的递推公式如下

(5)

边界条件为

(6)

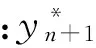
对于主缆缆段在竖直平面内的有应力长度dy,i可由下式确定:

dy,i=Si+ΔSy,i=

(7)

需要指出的是，采用第1种表达，需要迭代，初值为dy,i=Si，直至前后2次dy,i的差值满足误差允许；本文采用第2种表达.

2.2水平投影面

根据假定(1)，主缆在各节点处受吊杆横向分力Pz,i的作用，计算图式如图2所示.

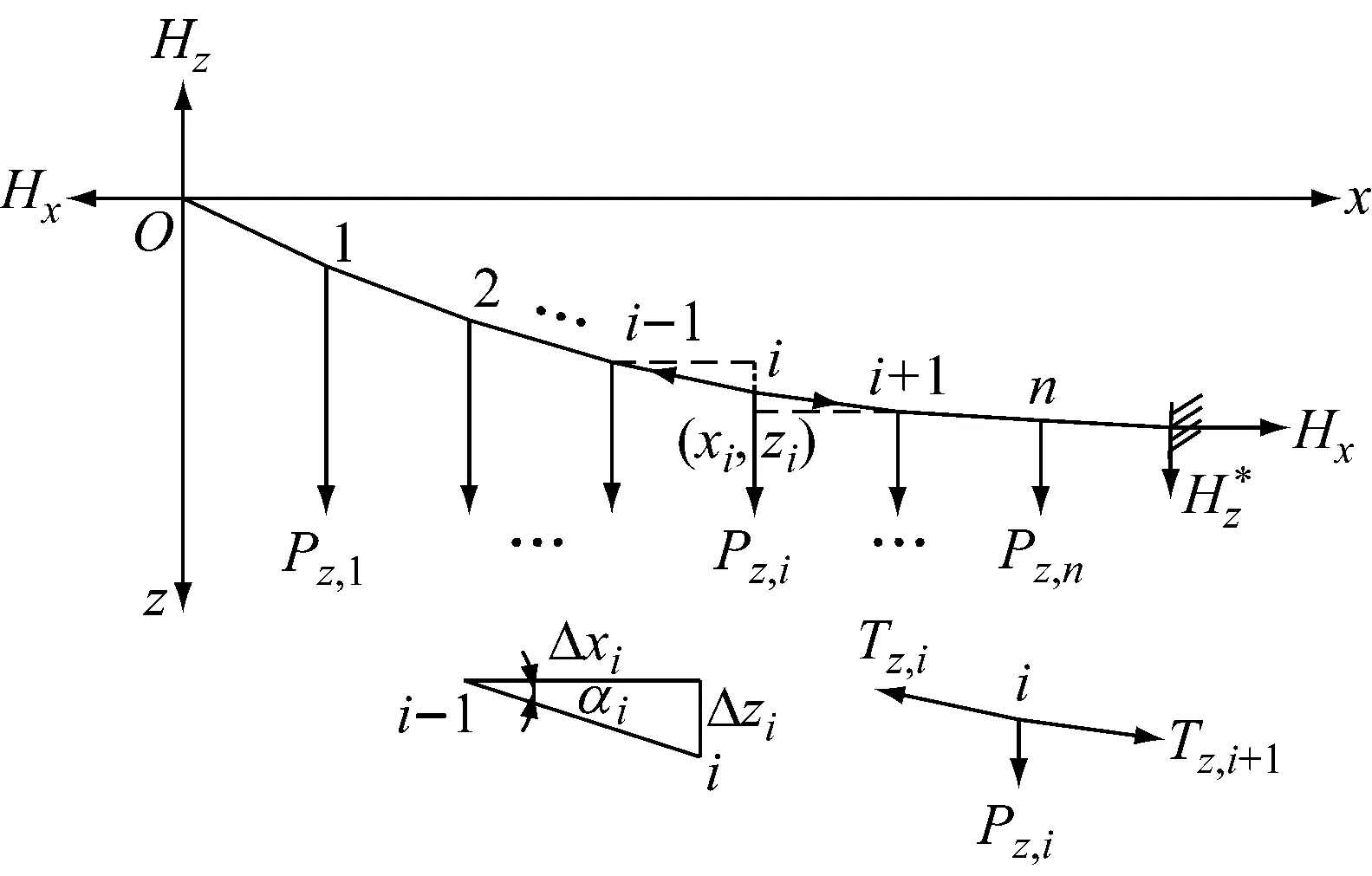
图2　主缆水平投影面计算图式

如图2所示，以节点i为研究对象.在水平投影面内，节点i在主缆与吊索的横桥向分力作用下保持平衡，即

(8)

当把斜吊索简化为二力杆时，Pz,i可用下式表达:

Pz,i=

(9)

其中，dd,i为吊索的有应力长度，zd,i为吊索梁端锚固点的横桥向坐标.dd,i可用下式计算:

dd,i=Sd,i+ΔSd,i=

(10)

式中:Ed、Ad分别为吊索的弹性模量和面积.与主缆缆段类似，若采用第1种表达，需要迭代，初值为dd,i=Sd,i，直至前后2次dd,i的差值满足误差允许.本文采用第2种表达.主缆吊点的横桥向坐标zi递推公式为

(11)

边界条件为

(12)

3　吊装阶段平衡状态的分段悬链线解

3.1基本方程

对于空间索形悬索桥，在主梁吊装过程的各个阶段中，在竖向荷载作用下，两吊点间的缆段总在一个铅垂面上.受横桥向倾斜的吊索力影响，各缆段在水平面上的投影与桥轴线的夹角各不相同，计算图式如图3所示.

图3　空间索形主缆计算图式

各缆段在各自铅垂面内满足

(13)

3.2递推公式

对于主梁吊装过程临时体系达到的力学平衡中，式中已知量为：主缆缆段的下料长度Si、弹性模量E、面积A、单位长度重力q；吊索单位长度重力qd，下端竖向分力Py,i，以及吊索下料长度Sd,i.未知量为：主缆吊点坐标xi、yi、zi，主缆张力的3个分力Hx,i、Hz,i、Vi，吊索横向分力Pz,i.

如图3所示，结合图1，可建立主缆吊点坐标xi、yi、zi的递推式为

(14)

根据计算图式(图1和2)，建立力的递推式

(15)

边界条件为

(16)

4　主索鞍偏移量

在主梁吊装过程中，为了保证主塔不受水平推力作用，需要使得主跨与边跨顺桥向水平力相等，即需要在不同工况下调整主索鞍的偏移量Δsk.

本文针对无吊杆形式的边跨，建立第k边跨的平衡方程为

(17)

式中:Sb,k、Lb,k、hb,k皆为已知量，分别为边跨k的主缆下料长度、成桥状态下散索鞍与主索鞍IP点的平距与竖距；Δsk与Vb,k为未知量，分别指边跨k处主索鞍的偏移量、主索鞍处的竖向力.其他符号与主跨一致.

5　算例

一座双塔单跨空间索形悬索桥(见图5)，跨径布置69 m+240 m+69 m，中跨竖向矢跨比为1∶6.8，塔顶IP点与吊杆下锚点横向距离为7.132 m.主要构件的材料特性和截面特性见表1.边跨为混凝土箱梁，中跨采用钢箱梁.

图4　桥型布置图

中跨主梁采用吊装施工方案，吊装工况见表2.

分别采用本文2种解析方法，应用编制的程序SASB-HCPA对算例求解，同时为了验证精度，结果与有限元软件BNLAS进行了对比.

表1　材料特性

表2　吊装施工工况

5.1主索鞍偏移量

主索鞍偏移量见图5，图中的柱状曲线代表本文方法与悬索桥专用有限元软件的差值.由图可见，各施工工况下主索鞍偏移量的精度都很好，有限元解与分段悬链线解相差不超过1 mm，二力杆解最大偏差小于3 mm，能够保证工程精度.

5.2主缆节点坐标

图6～8给出各工况下主缆跨中节点坐标的变化情况.

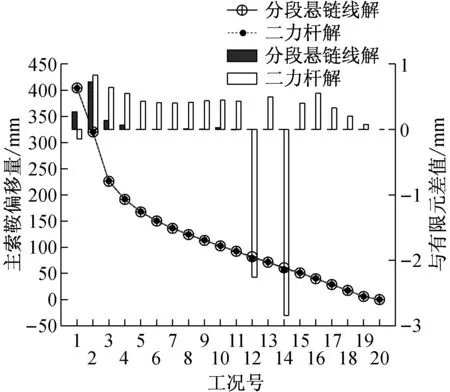
图5　主索鞍偏移量

就竖向坐标而言，分段悬链线解、有限元解两者吻合很好(见图6)，最大偏差为7 mm，偏差表现为随机正负摇摆，未呈现系统性规律，属于数值迭代差异.采用二力杆解的主缆跨中节点(见图6)，在空缆状态和成桥状态下，偏差为2.7 cm；在吊装过程的其他工况与分段悬链线解存在不超过18.4 cm的偏差；偏差规律表现为系统性偏大，呈两头小中间大，即空缆状态和成桥状态偏差最小，吊装过程的其他工况偏差增大.

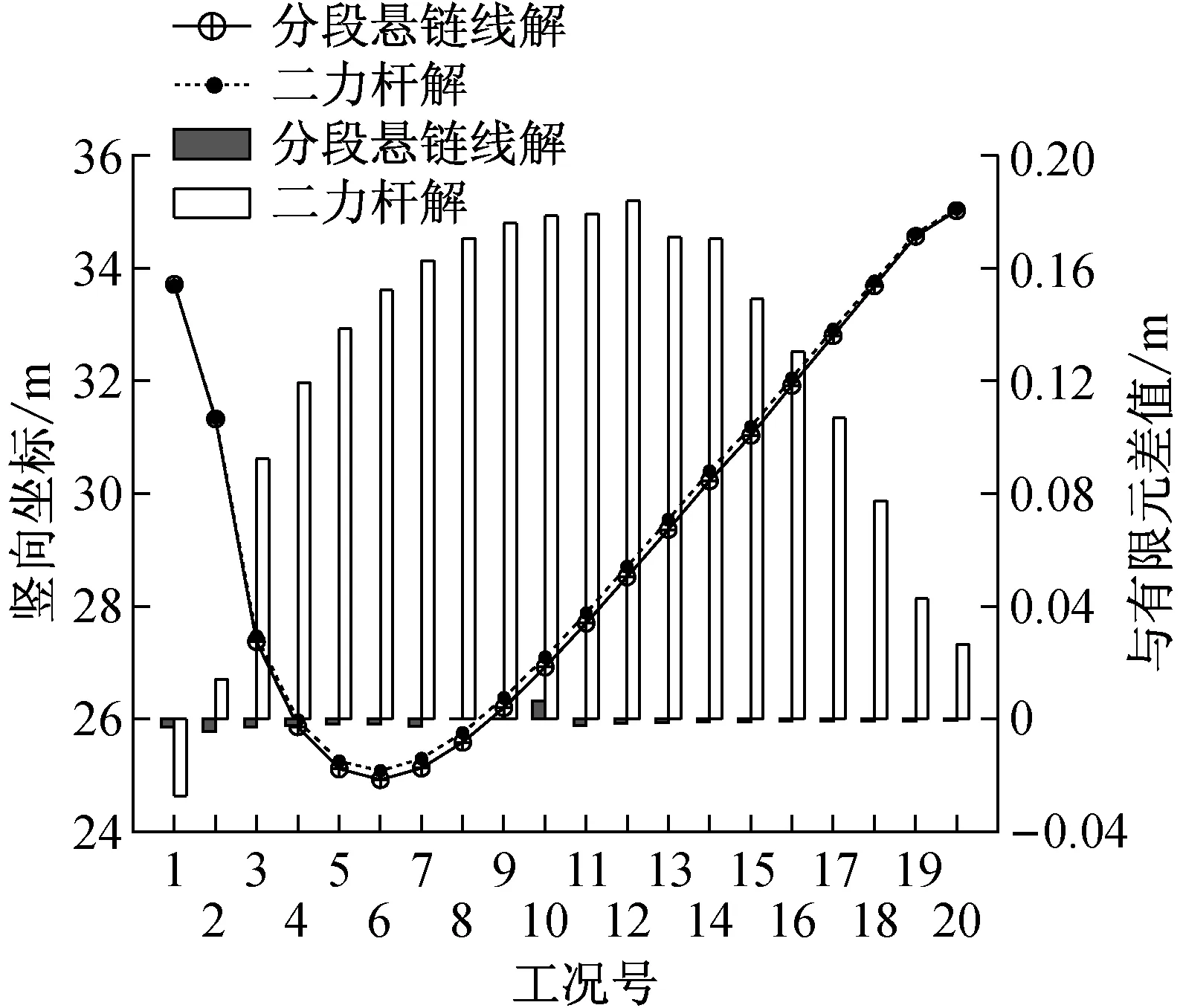
图6　跨中节点竖向坐标

就横向坐标而言，分段悬链线解、有限元解两者吻合很好(见图7)，最大偏差为7 mm，偏差呈现系统性偏大.采用二力杆解的主缆跨中节点(见图7)，最大偏差为2 cm；偏差规律表现为系统性偏大，呈两头小中间大，即空缆状态和成桥状态偏差最小，吊装过程的其他工况偏差增大.

就顺桥向坐标而言，分段悬链线解、有限元解基本一致(见图8)，除了10号工况在跨中有4 mm偏差外，其余工况偏差不超过1 mm，属于数值运算差异.采用二力杆解的主缆跨中节点(见图8)，最大偏差为6.0 cm，发生在空缆状态；随着吊装的进行，跨中节点偏差逐渐减小，成桥状态时偏差为4 mm.

图7　跨中节点横向坐标

图8　跨中节点顺桥向坐标

6　结语

本文针对空间索形悬索桥，在已有研究基础上，建立了此类桥型的吊装施工过程分析方法.本文方法不仅可以求解吊装施工全过程，也可以无需依赖于上一阶段的效应状态而单独求解任意工况.应用本文方法，可以方便地进行吊装过程的正装、倒拆分析，以及任一吊装阶段的单独分析，非常适合当前工况的影响因素规律分析，能迅速给出施工现场变动引起的理论值变化，有效解决上述施工过程实时分析的时效性问题，是有限元方法的一个有益补充.

参考文献:

[1]王晓明,郝宪武,石雪飞,等. 特大跨悬索桥的缆索体系优化[J]. 昆明理工大学学报:理工版, 2008, 33(6): 55.

WANG Xiaoming, HAO Xianwu, SHI Xuefei,etal. The large span suspension bridge cable system optimization [J]. Journal of Kunming University of Science and Technology:Technology, 2008, 33(6): 55.

[2]Kim H-K, Lee M-J, Chang S-P. Non-linear shape-finding analysis of a self-anchored suspension bridge[J]. Engineer Structures, 2002, 24: 1547.

[3]Kim K-S, Lee H-S. Analysis of target configurations under dead loads for cable-supported bridges[J]. Computers and Structures, 2001, 79: 2681.

[4]田汉州.京杭运河特大桥设计计算与临时锚固分析研究[D]. 大连:大连理工大学,2006.

TIAN Hanzhou. The design and calculation of Jinghang Cannel Bridge and research on provisional anchor[D]. Dalian: Dalian University of Technology,2006.

[5]王晓明,李红玉,段瑞芳,等.大跨度自锚式悬索桥吊装施工方法及塔梁临时锚固装置:中国, ZL201520042747.3 [P].2015-01-21.

WANG Xiaoming, LI Hongyu, DUAN Ruifang,etal. Since the anchor span suspension bridge hoisting beam temporary construction methods and tower anchorage device: China, ZL201520042747.3 [P].2015-01-21.

[6]黄亮,赵云安,盛亮,等. 东苕溪大桥主桥设计思路[J]. 公路交通科技:应用技术版, 2014, 114(6): 280.

HUANG Liang,ZHAO Yun’an,SHENG Liang,etal. East Tiao stream bridge design ideas [J]. Highway Traffic Science and Technology: Technology, 2014, 114(6): 280.

[7]王晓明,郝宪武,段瑞芳. 基于Steffens-Newton法的空间索形悬索桥初始平衡状态分析[J]. 计算力学学报, 2011, 28(5): 717.

WANG Xiaoming, HAO Xianwu, DUAN Ruifang. The initial equilibrium state analysis for spatial cable suspension bridge based on Steffens-Newton method [J]. Chinese Journal of Computational Mechanics, 2011, 28(5): 717.

[8]王晓明,贺耀北,石雪飞,等. 空间索形自锚式悬索桥初始平衡状态分析[J]. 同济大学学报:自然科学版, 2010, 38(5): 625.

WANG Xiaoming, HE Yaobei, SHI Xuefei,etal. Initial equilibrium state analysis of self-anchored suspension bridge with spatial cable[J]. Journal of Tongji University: Natural Science, 2010, 38(5): 625.

[9]周勇,张峰,叶见曙,等. 悬索桥空间主缆分析[J]. 东南大学

学报:自然科学版, 2009, 39(1): 101.

ZHOU Yong, ZHANG Feng, YE Jianshu,etal. Analysis of spatial cable of suspension bridge [J]. Journal of Southeast University: Natural Science Edition, 2009, 39(1): 101.

[10]韩艳,陈政清,罗世东,等. 自锚式悬索桥空间主缆线形的计算方法[J]. 湖南大学学报:自然科学版, 2007, 34(12): 20.

HAN Yan, CHEN Zhengqing, LUO Shidong,etal. The calculation method of spatial cable configuration self-anchored suspension bridge [J]. Journal of Hunan University: Natural Sciences, 2007, 34(12): 20.

[11]李传习,柯红军,刘海波,等. 空间主缆自锚式悬索桥成桥状态的确定方法[J]. 工程力学, 2010, 27(5): 137.

LI Chuanxi, KE Hongjun, LIU Haibo,etal. The finished state determination method of spatial cable self-anchored suspension bridge [J]. Engineering Mechanics, 2010, 27(5): 137.

[12]杨孟刚,陈政清. 自锚式悬索桥施工过程模拟分析[J]. 湖南大学学报: 自然科学版, 2006, 33(2): 26.

YANG Menggang,CHEN Zhengqing. An analysis of construction stages simulation for self-anchored suspension bridges[J]. Journal of Hunan University: Natural Sciences , 2006, 33(2): 26.

[13]牛登辉,周志祥,吴海军,等.自锚式悬索桥体系转换过程的无应力状态控制法[J]. 重庆交通大学学报:自然科学版, 2014, 33(1): 21.

NIU Denghui, ZHOU Zhixiang, WU Haijun,etal. Method of stress-free status in transition process of structural system for self-anchored suspension bridge[J]. Journal of Chongqing Jiaotong University: Natural Science, 2014, 33(1): 21.

[14]王邵锐,周志祥,吴海军. 超大跨自锚式悬索桥施工过程中力学性能的试验研究[J]. 土木工程学报, 2014, 47(6): 70.

WANG Shaorui, ZHOU Zhixiang, WU Haijun. Experimental study on the mechanical performance of super long-span self-anchored suspension bridge in construction process [J]. China Civil Engineering Journal, 2014, 47(6): 70.

[15]李方柯. 自锚式斜拉-悬吊组合体系桥梁主梁施工方法分析及模型试验研究[D]. 成都:西南交通大学, 2012.

LI Fangke. Research on main girder’s construction control of the self-anchored cable-stayed suspension composite system bridge and experimental investigation[D]. Chengdu:Southwest Jiaotong University, 2012.

收稿日期：2015-09-28

基金项目：国家自然科学基金(51308055); 教育部高校博士新教师基金(20130205120001); 中国博士后科学基金(2013M532000); 中央高校基本科研业务费专项资金(CHD2013G1211010)

中图分类号：U448.25

文献标志码：A

Analysis Method for Hoisting Construction Process of Suspension Bridge With Spatial Cables

WANG Xiaoming1,2, HE Yaobei3, CHEN Duo4

(1. Institute of Bridge Engineering, Chang’an University, Xi’an 710064, China; 2. Key Laboratory of Bridge Detection Reinforcement Technology of the Ministry of Transport, Chang’an University, Xi’an 710064, China; 3. Transportation Planning Survey and Design Institute of Hunan Province, Changsha 410008, China； 4. Shanghai Municipal Engineering Design Institute (Group) Co., Ltd., Shanghai 200092， China)

Abstract：Based on the fabrication length of main cable and hangers and the installation location of cable clamps, the lower end force matrix of hanger was established, and independent equilibrium equations of temporary system were established for each construction stage. Multi-segment two-force bars considering gravity and multi-stage spatial catenary were respectively employed to simulate bidirectional sag characteristics of spatial cables, and two analytical methods were proposed for construction processes during hoisting girder. The proposed methods can separately solve the physical effect of any construction stages, without depending on the effect of any previous stages. The example shows that the proposed methods can rapidly respond to the real-time changes of construction state, and are very suitable for the real-time monitoring of construction process and technical decision analysis.

Key words：suspension bridge; spatial cable-hanger system; construction process; two-force bar; multi-segment spatial catenary

第一作者： 王晓明(1983—),男,副教授,工学博士,主要研究方向为桥梁安全评估与工程控制.E-mail:wxm512061228@gmail.com