基于遗传算法的多服务模式公交优化设计

杨熙宇， 暨育雄， 王同根

(同济大学 道路与交通工程教育部重点实验室， 上海 201804)



基于遗传算法的多服务模式公交优化设计

杨熙宇， 暨育雄， 王同根

(同济大学 道路与交通工程教育部重点实验室， 上海 201804)

摘要：基于独立公交走廊需求特征，利用公交客流起点到终点(OD)数据，建立了以发车频率和公交车型为主要输出参数的多服务模式公交优化设计模型.针对模型求解的复杂性，应用遗传算法进行求解.最后，结合上海公交737路公交客流走廊数据给出了优化算例.结果表明，模型具有较强的实用性，能快速有效地求解出多服务模式的公交优化组合.

关键词：交通规划； 多服务模式公交； 公交走廊； 遗传算法

城市公共交通在城市客运交通体系中处于骨干地位，是大客流输送的主要方式，其客运功能的实现往往需要多服务模式公交的紧密配合.目前，除全程公交以外的公交模式主要有大站公交和区间公交，以下简称大站车和区间车.图1所示公交线路1为全程车模式，线路服务沿线有7个公交站点；公交线路2为大站车模式，服务沿线有3个重要的客流公交站点；公交线路3为区间车模式，服务固定区间段内的公交站点.以上3种不同公交模式共同设置在同一公交客流走廊上，如何优化协调设计此类多服务模式公交问题，已经成为当前研究的重点.

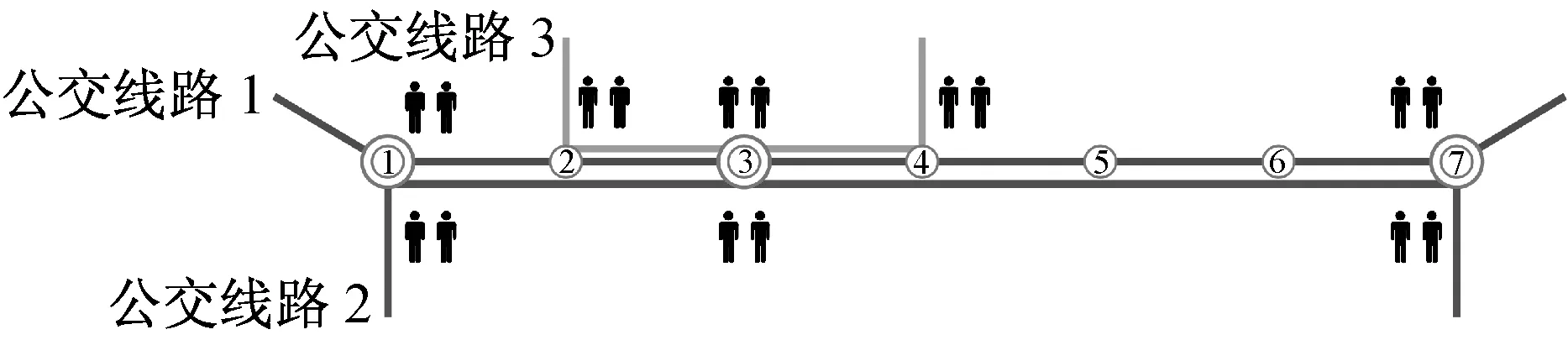
图1　多服务模式公交服务示意图

多服务模式公交优化问题的研究最早可追溯到1987年，Furth[1]将研究的重点集中在多服务模式公交的优化协调问题上，以发车频率和车头时距偏差作为模型重要的输出参数，但目标函数没有反映公交总成本对多服务模式公交优化的影响[1].后续的研究逐渐克服了这一缺点，采用不同的数理模型优化成本目标函数[2-7].其中，Site等[2]在模型中考虑了多服务模式公交之间换乘时间费用，从而使模型更加符合实际情况.Leiva等[4]将双层模型的适用性推广到多服务模式公交优化问题中，并且其适用性和有效性也得到了证明.以上这些研究关注的重点都在公交服务主体，对公交服务客体(乘客)的关注微乎其微.

直到近些年来，研究的热点才逐渐由公交服务主体导向转变为公交服务客体导向，模型中更加着重考虑公交自身服务对乘客的影响.2013年，Ceder等[6]通过对公交容量进行定义，针对不同的公交模式采用不同的容量公交车，并应用公交线路起点到终点(OD)计算出不同模式下的优化指标，结果表明乘客对于公交容量的敏感性较高，公交运行距离越长，容量要求就越高.2015年，Larrain等[7]利用已知的出行OD，假定公交存在拥挤和非拥挤2种状态，分别就两类状态建立优化模型求解多服务模式公交的发车频率.

就多服务模式公交优化设计的方法而言，从国内外的研究现状来看，主要存在如下问题：首先，考虑公交服务对乘客影响的研究不多；其次，缺少对于多服务模式公交优化组合的深入探讨；再者，模型的求解算法大多还停留在传统的枚举法，求解过程繁杂且效率低下.

基于以上考虑，本文提出了在OD需求条件下基于遗传算法的多服务模式公交优化设计问题.以实际的公交线路为现实背景，分析多服务模式公交特征，解析优化设计的机理，建立实用模型，并应用遗传算法求解.

1　多服务模式公交优化设计问题

1.1问题描述

优质的多服务模式公交服务是体现公交运营“以人为本”的重要指标之一.多服务模式公交服务成本量化过程为将运行成本、等候时间成本和车内行驶时间成本综合量化为费用成本的过程.研究表明，多服务模式公交优化问题并不是简单的调度优化问题，更多地需要考虑各种模式之间的组合优化[8]，才能有效地提高公交的服务质量，多元化地满足不同乘客的出行需求.

由此定位，本文研究的是如何有效地在多服务模式公交优化模型中融入公交服务对乘客的影响，并考虑多服务模式的组合优化，最后应用遗传算法快速高效求解.为简化叙述起见，将乘客上车点定义为出行的起点O点，乘客下车点定义为终点D点，OD出行叠加到公交线路上，每个出行者在出行过程中都形成一条出行路径.

1.2建模环境

1.3目标的选取

本次研究目标针对多服务模式公交车辆运行，采用协调优化策略，车辆资源调度面向指定线路的客运运输任务.在线路客流需求确定的情况下，其总成本主要通过优化发车频率和车型来控制.

以往的研究中[4]，以总成本最小为优化目标建立了多服务模式公交模型来提高系统的运行效率.因此，下文在以往研究的基础上考虑公交对乘客的影响，改进以往模型，建立以最小总成本为优化目标的多服务模式公交优化模型.本文对于建模作如下的假设：

(1) 线路运营完全独立,不受相邻线路的影响.

(2) 服务需求独立于发车频率和车型.

(3) 乘客服务服从“先到先服务” 的原则, 即先到达车站的乘客先上车.

(4) 站间区间内车辆运行速度为恒定值, 且途中无特殊事件发生.

(5) 研究时段内车辆发车间隔不变, 各公交站点均相同.

(6) 乘客对公交服务的感知受乘客所处状态(座位、站立或拥挤程度)和乘坐公交的时长有关.

2　模型建立

2.1目标函数

建立以公交自身的运营成本、乘客候车时间成本和车内时间成本总和为最小的目标模型.

(1) 单位时间公交运营成本c1

单位时间内的公交运营成本c1与车型大小、公交线路长度和发车频率成如下函数关系[4]：

(1)

(2) 单位时间乘客候车成本c2

假设公交车辆到达公交站点服从泊松分布，候车成本与发车频率成反比,和站点上车人数成正比，且不同模式的公交乘客候车时间还与不同模式的公交发车间距存在如下关系[2]：

(2)

式中：hr为全程车的车头时距，等于全程车发车频率的倒数.

基于上述假设，单位时间乘客候车成本如下所示：

(3)

(3) 单位时间车内时间成本c3

(4)

其中,

(5)

综合以上论述，目标函数为以上三部分总成本之和的最小值，即

(6)

2.2约束条件

上述3个模型中变量存在如下约束条件:

(7)

fr≥0, i∈N

(8)

(9)

2.3遗传算法

遗传算法是模拟生物遗传进化机制而发展起来的启发式算法，是一种模仿生物界自然选择原理和自然遗传机制的随机搜索最优算法，具有“生物+检测”特性.遗传算法的过程主要分为选择、交叉、变异和用作下一代4个主要步骤，如图2所示.

基于上述理论，本次研究通过以下7个步骤求解多服务模式公交优化设计问题：

步骤1初始化.初始化多服务模式公交初始方案、交叉概率以及变异概率，利用设定的选择价值产生种群.

步骤2评估染色体.对种群中的每个染色体进行目标值计算.

步骤3检验.更新选择最佳值，如果产生的数量超过了预先设定的门槛，停止计算.

步骤4计算产生的适应性.计算所有的染色体选择适应性概率.

图2　遗传算法过程示意图

步骤5选择父母.基于选择性概率来选择优秀的父母个体.

步骤6执行交叉.交叉父母来产生下一代.只有在产生染色体可行的情况下，下一代染色体才能替代父母.

步骤7执行变异.

3　实例应用

以上海公交737路作为研究多服务模式公交的样本，该线路途经18个公交站，选择早高峰时刻对该线路各公交站点上下客人数进行多次调查.经统计分析，通过已有的公交OD反推模型得到各站点的OD数据[9]，如表1所示，并将OD叠加到公交路段上，各站点间路段客流量统计如图3所示.

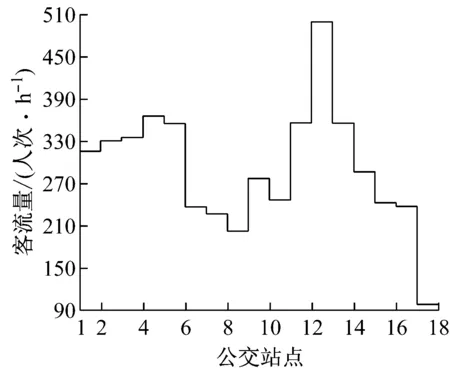
图3　公交站点间公交客流量示意图

针对客流量数据，采用遗传算法进行计算，种群规模取18，交叉概率取0.85，变异概率取0.2[7].最终通过不少于180次的收敛计算出最小目标函数值为6 124元，计算收敛迭代过程如图4所示.

对多模式优化计算和单模式(仅全程车模式)计算的结果进行对比，结果表明，多服务模式公交优化组合比单模式服务减少总成本约15.4%.如图5所示，多模式优化方案中大站车公交线的服务站点为1、9、11、12和18，区间车公交线路的服务站点为9、10、11、12、13、14和15.

表1　公交客流OD矩阵

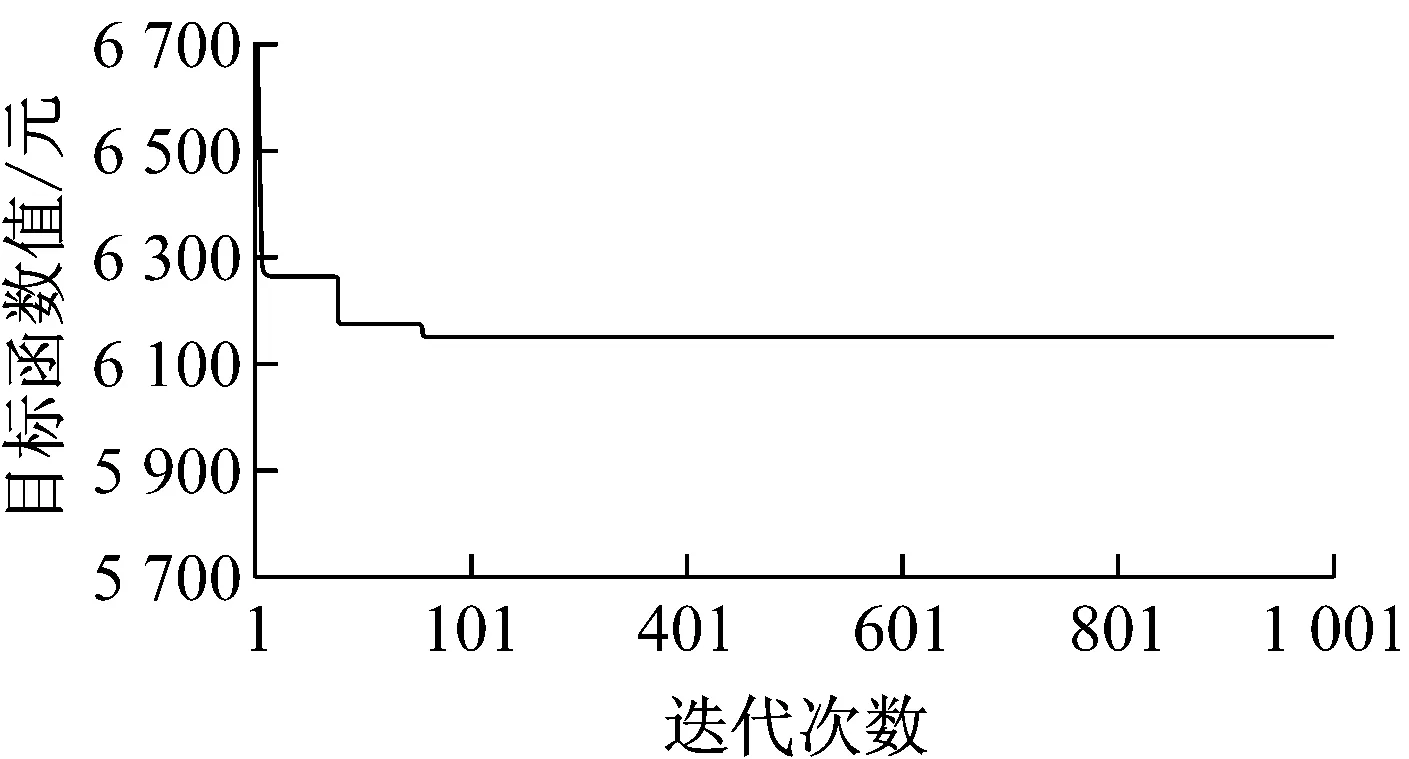
图4　遗传算法计算收敛过程图

3条不同模式的公交线路在客流交集的8个站点存在一定的客流竞争，如出行起点为站点9到终点为站点11的乘客，存在3种不同的选择竞争(全程车、大站车和区间车).沿线存在客流竞争的8个站点的多服务模式公交客流竞争结果如图6所示.结果显示，全程车随着经过站点数目的增大，客流竞争力下降；反之，大站车和区间车随经过站点数目的增加，客流竞争力上升.

图5　多服务模式公交优化设计结果示意图

本次研究的优化模型与Furth提出的传统模型[1]对比结果如表2所示.分析表明，车内时间成本比Furth模型显著增加25.95%，同时对车型容量的大小要求下降约6.67%.造成这类差异的主要原因为模型中加入服务水平对乘客影响这一重要因素，这样大大提高了公交服务水平.

对优化模型和传统模型计算结果在重要节点的

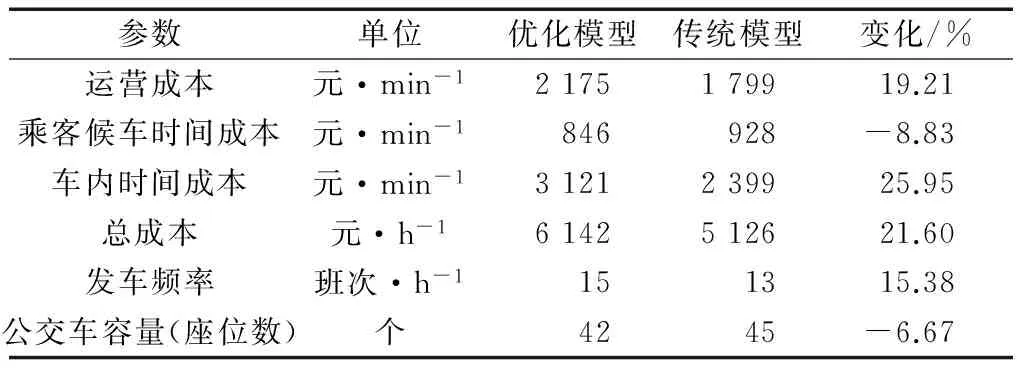
表2　优化模型与传统模型结果比较

图6　多服务模式公交站点客流竞争百分比示意图

客流变化进行统计分析，结果如图7所示.公交车内人数达到一定数量，车内逐渐拥挤的情况下，优化模式的公交车吸引力将下降，也就是说乘客可能会选择继续等候下一辆其他模式的公交车，这也是本次优化模型中加入容量参数，强调公交服务水平的原因.这一结论和现实情况有很强的一致性.

a 全程车

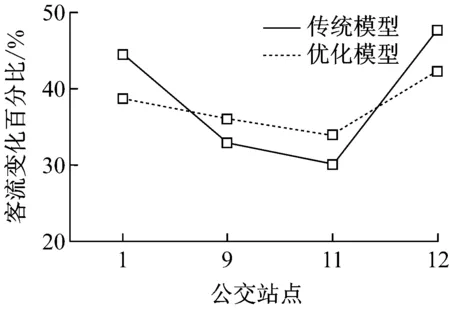
b 大站车

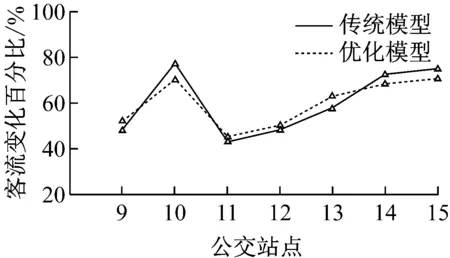
c 区间车

在优化模型不变的情况下，逐渐放大交通需求量，将原有的矩阵乘以相应的系数进行扩大，如图8所示.结果表明，优化模型和传统模型之间随需求的增大，计算的函数值也逐渐加大.

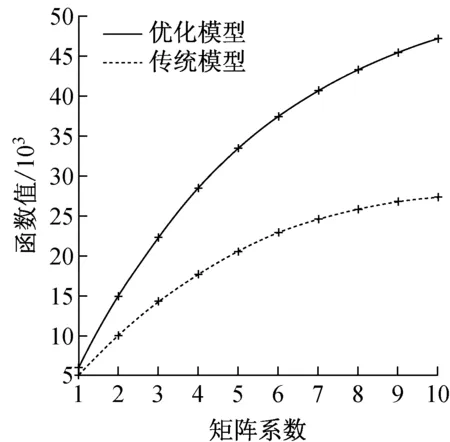
图8　不同交通需求下优化模型和传统模型的敏感性分析

Fig.8Sensitivity analysis of optimization and traditional models with different demands

对研究案例中的大站车和区间车线路进行组合研究，如图9所示，当大站车的线路为1条，区间车线路为2条时，目标函数取得最小值.

图9　不同模式公交线路组合敏感性分析

为了检验遗传算法的效率，本文对公交站点个数从10～18进行了不同方案下的计算效率统计,如表3所示.随着车站数量的增加，运行的次数并没有显著增加，运行的误差率也基本维持在10%左右.

4　结语

本文基于公交站点OD出行数据，考虑公交服务对乘客的影响，构建多服务模式公交优化模型，并应用遗传算法求解.该方法不仅能真实地反映乘客的出行成本，同时能够优化公交运营调度系统，对发车频率和车型大小提出了新的要求，且运用遗传算法克服了传统枚举法繁杂、效率低下的特点.

本文提出的多服务模式公交优化模型，从理论上可以推广到多服务模式公交网络的优化，但实际上由于网络问题有一定的复杂性，可能会导致计算过程中收敛于指定线路的最优值并非整个系统的最优值.同时本文提出的公交服务对公交乘客的影响中没有对在车内有座位和无座位的人群进行区分，尤其是在考虑先站立到有座的情况下，模型变得相对复杂，进一步的研究工作可以考虑在模型中加入新变量来完善.

表3　遗传算法敏感性分析

注：误差指遗传算法找到的优化值与传统算法之间的差异.

参考文献:

[1]Furth P G. Short turning on transit routes[J]. Transportation Research Record, 1987, 1108: 42.

[2]Site P D, Filippi F. Service optimization for bus corridors with short-turn strategies and variable vehicle size[J]. Transportation Research Part A: Policy & Practice, 1998, 32(1):19.

[3]Homero L, Ricardo G, Juan C M. Choosing the right express services for bus corridor with capacity restrictions[J]. Journal of the Transportation Research Board, 2010, 13(2197):63.

[5]Tirachini A, Cortés C E, Jara-Díaz S R. Optimal design and benefits of a short turning strategy for a bus corridor[J]. Transportation, 2011, 38(1):169.

[6]Ceder A, Hassold S, Dano B. Approaching even-load and even-headway transit timetables using different bus sizes[J]. Public Transport, 2013, 5(3):193.

[7]Larrain H, Muoz J C, Giesen R. Generation and design heuristics for zonal express services[J]. Transportation Research, Part E: Logistics & Transportation Review, 2015, 79:201.

[8]Ibarra-Rojas O J, Delgado F, Giesen R,etal. Planning, operation, and control of bus transport systems: a literature review[J]. Transportation Research Part, B: Methodological, 2015, 77:38.

[9]周雪梅，杨熙宇，吴晓飞. 基于IC卡信息的公交客流起止点反推方法[J]．同济大学学报：自然科学版，2012，40(7)：1027.

ZHOU Xuemei, YANG Xiyu, WU Xiaofei. Origin-destination matrix estimation method of public transportation flow based on data from bus integrated-circuit cards [J]. Journal of Tongji University：Natural Science, 2012，40(7)：1027.

收稿日期：2015-08-11

基金项目：国家自然科学基金(51308410)；上海市科委项目(15DZ1204402)

通讯作者：暨育雄(1978—),男,副教授，工学博士,主要研究方向为公交管理与控制.E-mail：yxji@tongji.edu.cn

中图分类号：U491

文献标志码：A

Optimization Design of Multiple Services for Urban Bus Corridor With Genetic Algorithm

YANG Xiyu， JI Yuxiong， WANG Tonggen

(Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University， Shanghai 201804，China)

Abstract：Based on the urban transportation demand of bus corridor, this paper studies the optimization design of multiple services with urban transit. For the operation characteristics of bus lines, the optimization model of minimum costs in terms of waiting time, in-vehicle travel time and operator cost is developed with genetic algorithm(GA). An application of the model to the case of No.737 bus line in Shanghai shows that the optimization model is practical and effective for satisfying the demand of passengers and improving the operating efficiency of bus transit system.

Key words：public transit; multiple services; bus corridor; genetic algorithm(GA)

第一作者： 杨熙宇(1982—),男,博士生,主要研究方向为交通运输规划与管理.E-mail：yangxiyu001@163.com