异质性预期、投资者行为与房价波动：上海和广州的双城记*

张　浩

(广东外语外贸大学 金融学院，广东 广州 510240)



异质性预期、投资者行为与房价波动：上海和广州的双城记*

张浩

(广东外语外贸大学 金融学院，广东 广州 510240)

摘要：房地产市场中存在大量的投资者，其市场行为会使房价出现大幅的波动，从而引起市场不稳定。文章在引入投资者异质性预期假设的基础上，构建了包含房地产消费者、投资者、供给者在内的房地产市场均衡模型，分析了房地产市场中基本面型投资者和趋势型投资者的异质性行为对房价变动的影响，并利用上海和广州两个一线城市的实际数据进行了对比分析。研究结果表明：在房地产市场中，两类投资者对于未来房价不同的预期以及投资行为会引起房价的变动；上海投资者的行为整体上会使上海的房价始终处于不断上涨的趋势中，而广州投资者的行为会随着投资策略的转变而使静态下的“整体上推动房价趋势型变化”转变为“整体上将房价‘拉回’基本面价格”；房地产市场中的投资者占比会显著影响房价的变动趋势，当基本面型投资者占比上升时，房价偏离度和房价变动率降低，而当这类投资者占比达到峰值时，房价会出现拐点；投资者之间的策略转换速度也会通过引起基本面型投资者占比的变化，引起房价的频繁波动，而且策略转换速度越快，房价波动越频繁。

关键词：异质性预期；策略演化；房地产市场；房价

一、引言与文献回顾

近年来，我国住房市场投机盛行，房价快速上涨，房地产市场存在泡沫隐患。2008年，美国发生次贷危机，房地产市场价格波动被认为是罪魁祸首之一，逐渐引起各国政府的重视，纷纷纳入宏观经济管理中。西南财经大学中国家庭金融调查与研究中心对我国个人金融资产状况的调查显示，房产已经占到我国居民家庭净资产的62.9%，如果房地产价格出现大幅波动，必将引起经济和社会的动荡。早期的文献研究表明，房地产价格主要受到需求、成本等多方面因素的影响，其波动也由宏观基本面的变量波动所引起(李仲飞和张浩，2015)。因此，国内学者大多将房价波动归因于房地产开发信贷规模、实际利率、经济增长率、人口变动等宏观基本面因素(梁云芳和高铁梅，2007；周晖和王擎，2009；况伟大，2010；徐建炜等，2012)和市场预期(黄静等，2013；王先柱和杨义武，2015)。然而，对于外部因素没有发生较大变化时的房价波动现象，以上结论却无法给出很好的解释。

事实上，房价的波动很难用人口增长、成本增加以及经济基本面变化来解释(Shiller，2005)。Gallin(2006)以及Mikhed和Zemcik(2009)的研究表明，个人收入、房屋建造成本和人口等因素的变动已经无法解释美国2000年之后的房价波动。Quigley(1999)指出，对房价而言，尽管收入、利率、人口结构等基础因素起到了重要作用，但是它们的解释力度甚至不足50%。总之，房价的短期波动无法用基础因素来解释，而更多地可能是由购房者的行为所引起的。

那么，应该采用何种方法来研究房地产市场上的投资者行为呢？部分学者认为经典金融理论的同质代理人和理性预期假设可能是理论的突破点。Zeeman(1974)在突变理论框架下，引入了基本面分析者和技术分析者两类投资者，成功展示了股市在牛市与熊市之间转换的机制。20世纪90年代之后，异质代理人模型得到了迅速的发展。Day和Huang(1990)、Chiarella(1992)等通过建立异质代理人模型(heterogeneous-agentmodel，HAM)研究发现，异质代理人在市场中的相互作用可以引起市场波动，而且在没有外部随机干扰的情况下，市场的内部机制也会引起价格波动。在此基础上，Pagan(1996)、Lux(1998)以及Lux和Marchesi(2000)进一步建立了带有策略转换的HAM，并探讨了市场中参与者的策略转换对资产价格波动的影响。Brock和Hommes(1997，1998)构建的模型成为HAM的基准框架。在此基础上，大量相关研究表明，资产价格的变动在很大程度上取决于市场参与者的交易决策。Hommes(2005)指出，基本面分析者推动价格趋向均衡价格，技术分析者推动价格偏离均衡价格；当技术分析者的比例超过某一阈值时，价格在短期内会持续偏离均衡价格，而基本面分析者的均值回归策略则从长期决定了市场均衡价格。

随着异质代理人模型的不断完善，其应用也更加广泛，并逐渐被用来解释房价的波动现象。Kouwenberg和Zwinkels(2011)采用超额需求的价格调整法则，建立了一个包含基本面分析者和技术分析者的房地产HAM，并使用1962-2000年美国房地产市场数据进行了实证分析。结果表明，房地产市场参与者的异质性行为确实造成了美国房价的波动。Bolt等(2014)通过构建一个均衡定价框架下的HAM，研究了OECD中5个国家1970-2012年的房价波动现象，结果再次证实了HAM的结论。而Dieci和Westerhoff(2012，2013)则建立了包含实际需求和投资需求的HAM，使用动力系统方法讨论了各参数对系统均衡点的影响，研究了系统均衡点失去稳定性时的变化情况，并刻画了房地产市场中“繁荣-萧条”的周期性波动。

基于此，本文在分析房地产市场中不同参与者行为的基础上，建立了带有市场转换行为的异质代理人模型，并以上海和广州两个城市为样本进行了实证分析。与以往的研究相比，本文在基本假设中区分了房地产市场中的投资者和消费者，采用“净需求”的概念，考虑了房屋的市场再交易情况，并将房地产市场中存在折旧和动态供给行为纳入模型中。文章进一步探讨了上海和和广州两个一线城市的投资者行为对房价的影响，为异质代理人模型在我国房地产市场上的应用提供了实证依据。

二、理论模型

(一)房地产市场中的参与者行为

假设房地产市场中房产的需求方有两类：一是房产消费者，二是房产投资者。房产消费者以自住为目的购买房产，而房产投资者则主要通过房屋买卖差价来获利。假设房地产市场中投资者具有异质性，主要表现为对房价的预期存在差异以及由此带来的投资行为差异。本文参考Kouwenberg和Zwinkels(2011)以及Bolt等(2014)的研究，假设房地产市场中存在两类投资者：一类是基本面型投资者(f)；另一类是趋势型投资者(c)。

(1)

其中，α(0<α<1)为基本面型投资者预期未来房价向基准价格回归的速度。α越大，意味着当房价发生偏离时，基本面型投资者预期房价向基准价格回归的速度越快。

趋势型投资者则认为，未来房地产价格会继续保持目前的上涨或下跌趋势，因而其对未来房价的预期可以表示为：

Ec,t(pt+1)=pt+β(pt-pt-1)

(2)

其中，pt-1为t-1期的房价，β(β>0)为趋势型投资者预期未来房价的外推强度。β越大，意味着趋势型投资者对当前房价变化的反应越敏感。假设投资者在t期的房产持有量为Wt=f(pt)=φpt+φ，则从t期到t+1期，投资者的需求量(买入或卖出)可以近似表示为：

这样，基本面型投资者在t+1期的新增需求为：

(3)

其中，a<0意味着基本面型投资者下一期的需求与实际房价对基准房价的偏离程度负相关。即如果实际房价高于基准房价，基本面型投资者会认为房价过高，从而在下一期减少需求(卖出手中的房产)；而如果实际房价低于基准房价，基本面型投资者会认为房价具有投资价值，从而在下一期增加需求。趋势型投资者在t+1期的新增需求为：

(4)

其中，b>0意味着趋势型投资者下一期的需求与当期房价的变动正相关。即如果当期房价高于前期房价，趋势型投资者会认为房价未来会继续升高，从而在下一期增加需求；而如果当期房价低于前期房价，趋势型投资者会认为房价会继续呈下跌的态势，从而在下一期减少房产持有量(卖出手中的房产)。令Wf,t+1、Wf,t和Wc,t+1、Wc,t分别表示基本面型投资者和趋势型投资者在t+1期和t期的房产持有量，则有：

(5)

(6)

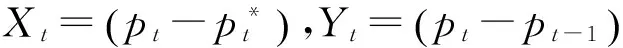
(7)

(8)

在房地产市场中，假设市场的新增供给由房地产开发商提供，新增供给量取决于开发商对价格变化的预期。记t+1期的新增供给为：

(9)

如果市场在t+1期达到均衡，则有：

(10)

(11)

(12)

如果t+1期市场处于均衡状态，则均衡价格pt+1可以表示为：

(13)

(二)投资者行为的演化

投资者会通过观察房地产市场的变化来不断优化自己的投资策略，实现投资收益最大化。因此，房地产市场中的投资者会根据市场的变化转换投资策略。本文假设两类投资者依据投资收益转换策略。两类投资者的投资业绩函数分别定义为：

(14)

(15)

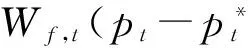
(16)

(17)

其中，κ(κ>0)为选择强度，衡量两类投资者信念演化的速度。当κ较大时，两类投资者的转换速度较快；如果κ→∞，则表明投资者对两类投资策略的收益越来越敏感。这意味着如果两种投资策略的收益稍有差异，投资者便会立刻转换投资策略。而如果κ→0，则ηf,t+1=ηc,t+1=0.5，这意味着市场中两类投资者各占一半，且相互之间不存在转换。进一步地，nf,t和nc,t可以表示为：

(18)

ηc,t+1=1-ηf,t+1

(19)

(三)基准房价的确定

(20)

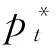
三、中国房地产市场中的投资行为与房价波动分析

(一)计量模型建立

pt+1=γ0+γ1pt+γ2ηf,t+1Xt+γ3ηc,t+1Yt+εt

(21)

(18)式也可以进一步表示为：

(22)

结合(19)式、(21)式和(22)式，可以得到如下的非线性方程系统：

pt+1=γ0+γ1pt+γ2ηf,t+1Xt+γ3ηc,t+1Yt+εt

ηc,t+1=1-ηf,t+1其中，γ1体现了房价的延续性，根据Shiller(1998)的结论，房价具有较强的正向自相关性，且由 (9)式和 (11)式中需求和供给的基本关系可知，ξ>0，m<0，故我们预期γ1>0。γ2体现了基本面型投资者对房价的影响，由于a<0，我们预期γ2<0，即实际房价偏离基准房价程度的增加会引起房价的下降。γ2<0反映了基本面型投资者的行为对于房价偏离的“拉回”能力。γ3体现了趋势型投资者对房价的影响，由于b>0，我们预期γ3>0，即趋势型投资者的行为会使房价延续之前的变化趋势。γ4体现了两类投资者之间的转换速度，我们预期γ4>0。

(二)数据选取

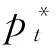
(三)房价偏离程度分析

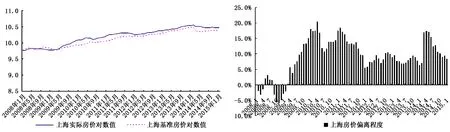
图1　2008年1月-2015年1月上海房价偏离程度

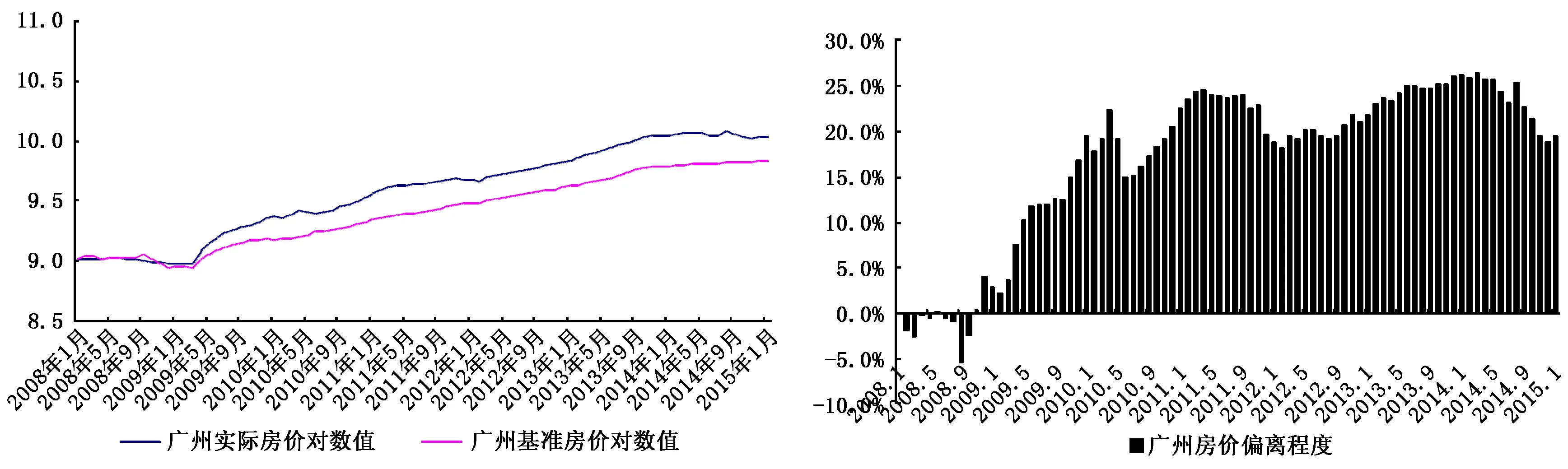
图2　2008年1月-2015年1月广州房价偏离程度

(四)投资者行为差异分析

表1　参数估计结果

注：括号内为p值。

表1中HAM回归结果显示，γ2<0，表明实际房价对基准房价的正向偏离会使其在下一期下降，体现了房地产市场中基本面型投资者对于房价偏离的拉回能力。γ3>0，表明房价的变动具有延续性，即当期房价的变动会影响下一期的房价，且两者同向变化。γ4>0，表明市场中两类投资者之间具有较快的转换速度，他们一旦发现另一种投资方式具有更高的收益，便会改变投资策略。这说明在HAM框架下，投资者存在投资行为的转换，上海投资者对于市场的变化更加敏感，投资策略的转换速度更快，房价波动的延续性也更加明显。这说明上海房产市场中趋势型投资者的力量更强，上海房价的上涨(或下跌)态势更加明显、速度也更快。这与上海现实的房价表现基本一致。

总体来看，无论是在HAM框架下还是在静态状态下，上海和广州两地房地产市场中的投资者对房价的影响基本一致，即趋势型投资者的市场行为会使房价进一步上涨，而基本面型投资者的行为则会使房价上涨的速度放慢。由于上海和广州两地房地产市场中投资者的作用不同，两地的房价变动程度存在较大差异。

四、投资者行为对房价影响的再分析：上海与广州的对比

(一)上海与广州的房价偏离度对比

图1和图2表明，与广州相比，上海实际房价偏离基准房价的程度始终处于较低水平，且从2011年开始，两地的这种差距呈现不断扩大的趋势。这意味着尽管上海的房价较高，但“泡沫”却相对较小。这主要是因为：上海作为国际金融中心，良好的区位优势吸引了大量外来人口；而上海本身城区面积较小，地处江苏和浙江之间，外扩难度较大；同时，上海的常住人口密度远大于广州，且收入水平较高，使得房租水平也较高，从而基准房价相对较高。此外，上海的房租与实际房价保持相近的上涨态势，因此相对而言，房地产市场“泡沫”问题并不突出。而尽管广州在一线城市中的房价水平并不高，但作为传统的区域性中心城市，随着近年来外来人口占比的逐渐降低，而行政区域面积相对较大，广州的人口密度在不断下降；此外，广州市区内存在大量城中村，居住着众多外来人员，使得广州的房租整体偏低，从而基准房价较低，其房地产市场“泡沫”反而较大。

表1结果已表明，相对而言，广州基本面型投资者的影响更大，这意味着广州的基本面型投资者可以在一定程度上缓解实际房价的持续偏离。但为什么广州反而出现了较大的房地产泡沫呢？我们猜测这可能与广州相对较低的基本面型投资者占比有关，本文将对此做进一步的深入分析。

从反映趋势型投资者的影响程度γ3来看，当κ→0和κ→∞时，上海和广州两地的差异并不明显；而一旦投资者的策略可以发生转换，即在HAM框架下，两地趋势型投资者的影响程度则出现明显差异。那么，这一变化是否会对房价变化产生影响？我们也将对此做进一步分析。

(二)投资者行为差异对房价的影响

当存在投资策略转换机制时，表1中HAM的结果表明，两类投资者会根据以往的投资经验和收益较为迅速地实现投资策略的转换。从数值上看，当发生策略转换时，γ2系数的绝对值都增大，而γ3的系数则减少，这可能是由ηf小于0.5所致，即两个城市的趋势型投资者占比较高，易引发市场泡沫。事实上，根据表1中的回归结果，利用(22)式可以计算出上海和广州基本面型投资者的占比。其中，上海基本面型投资者占比的均值为49.32%，广州的则为48.24%。由于上海和广州两地的基本面型投资者占比均值都接近50%，HAM框架下的回归结果较为接近κ→0时的情况。但广州相对较低的基本面型投资者占比导致市场中的投机行为较多，造成广州的房价尽管不高，但“泡沫”却较大。

为进一步分析HAM框架下两类投资者行为的差异，结合(21)式以及ηf和ηc的均值，可以得到投资者行为对下一期房价的影响，具体结果见表2。

注：当κ→0时，ηf=ηc=0.5；在HAM框架下，ηf的取值为均值，ηc=1-ηf。

(三)投资者占比与房价变化

从图3和图4中可以看到，当基本面型投资者占比上升时，房价偏离度和房价变动率呈现下降的趋势。当基本面型投资者占比达到峰值时，房价将出现阶段性的低点(房价变动率达到极小值)，房价变动率和偏离度也会出现阶段性拐点。而当基本面型投资者占比达到谷值(即趋势型投资者占比达到峰值)时，房价总是保持之前的变动趋势，要么继续冲高，要么继续回落，房价偏离度则呈现进一步扩大或缩小的态势。

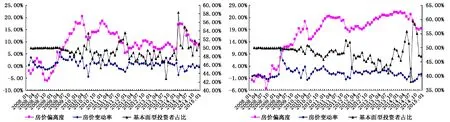
图3　上海基本面型投资者占比与房价偏离度和房价变动率的关系　　　　　　　　图4　广州基本面型投资者占比与房价偏离度和房价变动率的关系

结合表1以及图3和图4的结果，上海的投资者转换速度γ4相对较大，则ηf的变动较为频繁，使得上海房价的变动率和偏离度的波动也较为频繁，而广州房价的变动率和偏离度则相对稳定。这一结果也印证了Zhang等(2015)的结论。

综上所述，上海和广州等一线城市的房地产市场中存在大量市场投资者，且投资者存在异质的市场预期和投资行为，这会造成房价产生波动并逐渐偏离基准价格。从实际数据来看，上海和广州的房地产市场在具有共同上涨趋势的同时，又存在明显的差异化特征。这主要是因为在两个城市的房地产市场中，投资者占比及影响存在明显的差异。本文的研究为进一步揭示我国一线城市的房价上涨和波动存在差异提供了新的视角。

五、结论与启示

房地产市场中不仅存在具有“刚性需求”的消费者，还有大量投资者，由于各类投资者的行为存在差异，房价变动表现出不同的特征。分析投资者行为，对于解释当前房地产市场特别是一线城市的房价“暴涨”现象，具有一定的现实意义。本文从理论上构建了包含消费者、投资者和供给者的房地产市场局部均衡模型，通过引入投资者异质性行为假设，分析了房地产市场中基本面型投资者和趋势型投资者的异质性行为对房价变动的影响。文章进一步建立非线性方程系统，利用上海和广州两个一线城市的数据，采用非线性最小二乘法，实证分析了投资者的异质性行为对房价的影响，并比较了两个城市的差异。本文主要得到以下结论：

第一，在房地产市场中，基本面型投资者和趋势型投资者对于未来价格不同的预期以及各自的投资行为会引起房价的变动。实证结果表明，实际房价对基准房价的正向偏离会使房价在下一期下降，基本面型投资者对于房价偏离具有明显的“拉回”作用；而在趋势型投资者的作用下，房价变动具有延续性，当期房价的变动会进一步影响下一期的变动。

第二，在上海和广州两地，房地产市场中投资者行为的影响存在明显的差异。静态条件下，上海和广州两地房地产市场中的投资者对房价的影响差异并不明显；而一旦投资者行为发生了转换，两地趋势型投资者的影响程度则出现明显差异：广州趋势型投资者的整体影响不仅会变小，而且由于变化幅度过大，投资者行为对房价的整体影响会发生反转，即投资者行为会使静态下的“整体上推动房价趋势型变化”转变为“整体上将房价‘拉回’基准价格”。

第三，房地产市场中的投资者占比会显著影响房价的变动趋势。当基本面型投资者占比上升时，房价偏离度和房价变动率下降；当基本面型投资者占比达到峰值时，房价将出现阶段性的低点(或高点)，房价变动率和偏离度也会出现阶段性拐点；当基本面型投资者占比达到谷值时，房价总是保持之前的变动趋势，要么继续冲高，要么继续回落，房价偏离度会进一步扩大或缩小。房价正是在基本面型投资者占比的不断变化中呈现频繁波动的状态，而由于上海的投资者转换速度较快，其房价变动率和偏离度的波动较为频繁。

第四，投资者之间的策略转换速度也会通过引起基本面型投资者占比的变化而导致房价频繁波动。实证结果表明，上海的投资者转换速度相对较快，则其基本面型投资者占比的波动较为频繁，从而上海房价变动率和偏离度的波动也较为频繁。

整体上看，由于我国一线房地产市场中存在异质性的投资者，市场会出现不必要的波动，且投资者行为对房价变动会产生巨大影响。基于此，本文提出以下政策建议：一是规范一线城市房地产市场发展，严防部分城市房价过快上涨，通过强化购房条件、提高购房首付比例、从严认定购房资格、尝试推行房产税等方式，提高投资者成本，减少投资和投机行为，防止房价频繁大幅波动，维持楼市平稳健康发展。二是规范房地产市场预期，合理引导购房者的追涨心理。投资者的市场行为源于对未来房价的预期，因此当地政府需要合理引导房地产市场参与者的预期，正确引导社会舆论方向，从而实现市场预期管理，规范市场参与者的行为。

*本文还得到广东外语外贸大学高层次人才项目及科研创新团队项目(TD1604)的资助。

主要参考文献：

[1]黄静，王洪卫，柯昇沛.基于行为金融学的房价预期对地价的动态作用机制研究[J].财经研究，2013，(7)：134-144.

[2]况伟大.预期、投机与中国城市房价波动[J].经济研究，2010，(9)：67-78.

[3]李仲飞，张浩.成本推动、需求拉动——什么推动了中国房价上涨?[J].中国管理科学，2015，(5)：143-150.

[4]梁云芳，高铁梅.中国房地产价格波动区域差异的实证分析[J].经济研究，2007，(8)：133-142.

[5]王先柱，杨义武.差异化预期、政策调控与房价波动——基于中国35个大中城市的实证研究[J].财经研究，2015，(12)：51-61.

[6]徐建炜，徐奇渊，何帆.房价上涨背后的人口结构因素：国际经验与中国证据[J].世界经济，2012，(1)：24-42.

[7]Bolt W, Demertzis M, Diks C, et al. Bubbles and crashes in house prices under heterogeneous expectations[R]. Working Paper, 2014.

[8]Brock W A, Hommes C H. Heterogeneous beliefs and routes to chaos in a simple asset pricing model[J]. Journal of Economic Dynamics and Control, 1998, 22(8-9): 1235-1274.

[9]Day R H, Huang W. Bulls, bears and market sheep[J]. Journal of Economic Behavior & Organization, 1990, 14(3): 299-329.

[10]Dieci R, Westerhoff F. A simple model of a speculative housing market[J]. Journal of Evolutionary Economics, 2012, 22(2): 303-329.

[11]Hommes C H. Heterogeneous agent models in economics and finance[R]. Tinbergen Institute Discussion Paper No.TI05-056/1,2005.

[12]Hott C, Monnin P. Fundamental real estate prices: An empirical estimation with international data[J]. Journal of Real Estate and Finance and Economics, 2008, 6(4): 427-440.

[13]Kouwenberg R, Zwinkels R C J. Chasing trends in the U.S. housing market[R]. Erasmus University Rotterdam Working Paper, 2011.

[14]Lux T, Marchesi M. Volatility clustering in financial markets: A micro-simulation of interacting agents[J]. International Journal of Theoretical and Applied Finance, 2000, 3(4): 675-702.

[15]Mikhed V, Zemcik P. Do house prices reflect fundamentals? Aggregate and panel data evidence[J]. Journal of Housing Economics, 2009, 18 (2): 140-149.

[16]Pagan A. The econometrics of financial markets[J]. Journal of Empirical Finance, 1996, 3(1): 15-102.

[17]Quigley J M. Real estate prices and economic cycles[J]. International Real Estate Review, 1999, 2(1):1-20.

[18]Shiller R. Irrational exuberance[M]. 2nd ed. Princeton：Princeton University Press, 2005.

[19]Zhang H, Huang Y, Yao H. Heterogeneous expectation, beliefs evolution and house price volatility[J]. Economic Modeling, 2015, 53(2): 409-418.

(责任编辑康健)

收稿日期：2015-11-25

基金项目：国家自然科学基金项目(71231008，71373057，71402037)；教育部人文社科青年基金项目(14YJC790048)；广东省高等教育“创新强校工程项目”(GWTP-GC-2014-01)

作者简介：张浩(1983- )，男，陕西宝鸡人，广东外语外贸大学金融学院讲师，云山青年学者，金融学博士。

中图分类号：F830.9；F293.3

文献标识码：A

文章编号：1001-9952(2016)08-0051-12

DOI:10.16538/j.cnki.jfe.2016.08.005

Heterogeneous Expectation, Investor Behavior and Fluctuations in Housing Prices:Tale of Two Cities between Shanghai and Guangzhou

Zhang Hao

(SchoolofFinance,GuangdongUniversityofForeignStudies,Guangzhou510240,China)

Abstract：In real estate market, there are a lot of investors, and their market behavior leads to fluctuations in housing prices to a big margin, thus resulting in market instability. Based on the introduction of investors’ heterogeneous expectation assumptions, this paper builds up the equilibrium model of real estate market including real estate consumers, investors and suppliers. It analyzes the impact of heterogeneous behavior of fundamental-based and trend-based investors on fluctuations in housing prices and makes a comparative

study by using the real data of Shanghai and Guangzhou as two first-tier cities. It comes to the results as follows:firstly, in real estate market, different expectation of future housing prices by these two categories of investors and investment behavior can result in changes in housing prices; secondly, Shanghai investor behavior overall leads to constantly rising trend in Shanghai housing prices all the time,and Guangzhou investor behavior results in the transformation from overall pushing trend-based changes in housing prices under original static condition to overall pulling housing prices back to the fundamental prices with changes in investment strategy; thirdly, investor proportion in real estate market significantly affects change trend of housing prices; when the proportion of fundamental-based investors rises, the deviation and change rate of housing prices reduce, and when the proportion of fundamental-based investors reaches the peak, housing prices are at an inflection point; fourthly, the strategy change speed among investors also gives rise to changes in the proportion of fundamental-based investors and thereby frequent fluctuations in housing prices, and quicker strategy change speed leads to more frequent fluctuations in housing prices.

Key words:heterogeneous expectation; strategy evolution; real estate market; housing price