双目标规划问题的像集与求解
2016-08-11马赞甫刘妍珺
马赞甫 刘妍珺
摘要经济管理的决策目标往往与成本、收益相关,双目标规划在经济管理中具有广泛应用.然而,尚缺乏成熟的算法确定双目标规划问题的全部解.给出双目标规划问题像集的一般性确定法,以求其解,为研究目的所在.具体而言,构造一个带等式约束的单目标规划问题,以确定双目标规划问题像集之部分边界,并借助拉格朗日乘子符号判断其单调性,据此确定原问题的帕累托解与弱帕累托解.这相当于提供了一个求解双目标规划问题的一般性框架.
关键词最优化;双目标规划解法;单目标规划;像集;弱帕累托解
中图分类号F224-3 文献标识码A
AbstractThe objective of decisionmaking in economic management is often related to cost and benefit. A good case in point is that biobjective programming based on costbenefit analysis is widely used in economic management. However, so far, there is still a lack of mature algorithms to determine the full solution of the Bi objective programming problem. A general method, which was used to get the Pareto solution or weak Pareto solution for double objective optimization problems, was put forward in this research. To be specific, we constructed a single objective programming with equality constrain to determine the frontier of the image set of double objective optimization problems. Furthermore, we could determine the frontier's functional monotonicity using Lagrange multiplier and finally get the Pareto solution or weak Pareto solution. Base on above steps, A general framework was presented to solve double objective programming problem.
Key wordsOptimization, The Method of Solving DoubleObjective Programming, SingleObjective Programming, Image Set, Weak Pareto Solution
1引言
多目标规划的解法可区分为间接算法与直接算法两种.间接法的一般思路是将多个目标转换为单一目标进行处理,往往只能得到问题的一个解或部分解.如杨轶华、吕显瑞、刘庆怀等(2006)所指出的,间接法存在顾此失彼之缺点[1].直接法则以同伦法为代表,通过构造同伦映射确定多目标规划问题的解,直指多目标规划问题本身,可回避间接法之缺点.其中,刘庆怀、林正华(2000)考察采用该算法确定问题的最小弱有效解[2],而杨轶华、吕显瑞、刘庆怀等(2006)则采用该算法确定多目标规划问题的一个有效解集[1].
考虑到万事万物好与坏、收益与成本等双分类的普遍性,多目标规划中的双目标规划具有极为重要的应用价值,常用于企业管理决策[3-5]、交通设置优化[6-7]等现实问题.不失一般性,双目标规划问题的求解也可借助多目标规划求解方法.事实上,杨轶华、吕显瑞、刘庆怀等(2006)考虑了同伦内点算法在双目标规划求解中的应用[1],而曾玉华、彭拯(2010)同样考虑了双目标规划问题的一种直接算法,即非精确交替方向法[8].下文拟提出双目标规划的一个更具一般性的应用分析框架,从属于直接法,从问题的像集结构入手,试图确定问题的全部解.
2双目标规划相关概念
考虑如下一般形式的双目标规划问题:
min x∈Xθ1x,
min x∈Xθ2x.(1)
假设目标函数θ1x,θ2x都可微.
称xp∈X为其帕累托解,如果不存在x∈X,使得
θ1x≤θ1xp,
θ2x≤θ2xp.
且其中至少有一个为严格不等式.
称xw∈X为问题(1)的弱帕累托解,如果不存在x∈X,使得下列不等式组成立:
θ1x<θ1xw,
θ2x<θ2xw.
多目标规划问题的帕累托解或弱帕累托解其定义依据是目标函数值,因此,研究多目标规划问题的像集是求解多目标规划问题确定其帕累托解与弱帕累托解的最直接手段.特别是,双目标规划问题的像集不仅易于确定,且具有几何直观性,是求取双目标规划问题的便利工具.问题(1)的像集定义为
F=θ1x,θ2x|x∈X.(2)
与多目标规划问题的帕累托解与弱帕累托解相对应,可分别定义其像集中的帕累托点与弱帕累托点.
称θp1,θp2∈F为F中的帕累托点,如果不存在θ1,θ2∈F使得
θ1≤θp1,
θ2≤θp2.
其中至少存在一个严格不等式.
称θw1,θw2∈F为F中的弱帕累托点,如果不存在θ1,θ2∈F使得
θ1<θw1,
θ2<θw2.
显然,如果xp∈X为多目标规划问题的帕累托解,则其像θ1xp,θ2xp必为F中的帕累托点,反之亦然.类似地,如果xw∈X为问题的弱帕累托解,则其像θ1xw,θ2xw必为F中的弱帕累托点,反之亦然.基于此,可构造单目标规划问题确定双目标规划问题像集的基本特征,以达到确定其帕累托解及与弱帕累托解之目的.
2双目标规划像集的确定
确定像集的方法较多,不过,一般具有问题针对性.比如,单一决策变量事实上可定义双目标函数之间的一个参数方程,可采用消除变量方式确定目标函数之间的函数关系.又如,若问题为多目标线性规划形式,可采用凸组合方式确定像集[9].针对双目标规划问题,本项研究考察其像集的一般性确定方法.
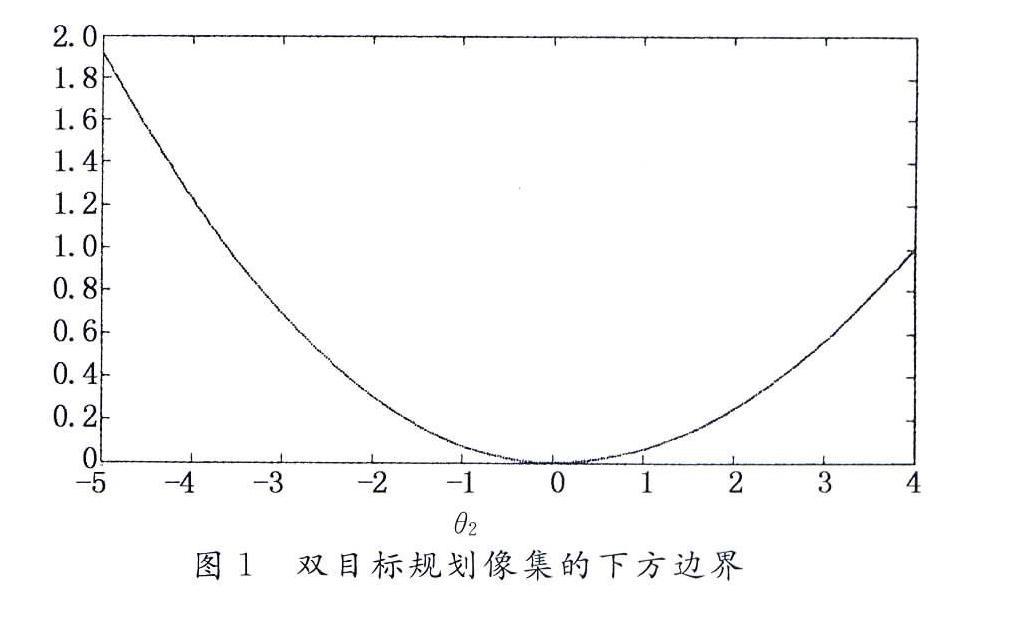
不论变量x维度如何,双目标规划问题的像集总是二维空间中的点集.因此,可通过探究像集的结构特别是下边界形式确定双目标规划问题的弱帕累托解.为此,考察如下单目标规划问题:
min θ2x,
s.t.θ1x=θ1,x∈X.(3)
其中θ1∈θ1x|x∈X.问题(3)旨在界定多目标规划问题像集的下方边界.该问题为等式约束问题,按照通常的做法,就x∈X,构造拉格朗日函数
Lx,λ=θ2x+λθ1-θ1x.
问题的一阶条件等价于如下方程组:
θ1x=θ1,θ2xx=λθ1xx.
这里θixx为函数θix的梯度向量,i=1,2.针对给定的参数θ1,假设存在满足拉格朗日条件的xθ1与λθ1,其中xθ1∈X为问题(3)的最优解,记相应的目标函数最小值为θ2θ1.
现需要判断单目标规划问题的最优解是否为多目标规划问题的帕累托解.
若θ2θ1在θ1处可导,且λθ1>0,则根据包络定理(Envelope Theorem)有[10]
dθ2θ1dθ1=λθ1>0,
或者说函数θ2θ1在θ1处单调递增,这表明xθ1并非多目标规划问题的弱帕累托解.
反之,若λθ1<0,此时
dθ2θ1dθ1=λθ1<0.
表明在xθ1的某领域范围内,两目标函数之间存在此消彼长关系,xθ1为多目标规划问题的局部帕累托解.除此之外,若λθ1=0,暂不能确定xθ1是否为双目标规划问题的弱帕累托解.
综上,利用单目标规划问题确定多目标规划问题的解,主要关注如下两点:其一,给定参数θ1一个可能的取值,函数θ2x能否在方程θ1x=θ1的解集中取到最小值.如果单目标规划问题最优值负无穷,则满足θ1x=θ1的可行解满足帕累托解的定义,是多目标规划问题的帕累托解.换言之,即便2θ1在θ1处无定义,也不影响求取双目标规划问题的帕累托解.
其二,该最小值点是否满足局部弱帕累托性,即相应的拉格朗日乘子符号如何.若乘子为负,则单目标规划问题的解是多目标规划问题的局部弱帕累托解,否则该解并非弱帕累托解.当然,如果目标函数满足凸性,局部弱帕累托解必然是整体弱帕累托解.
进一步地,若就每一个可能的θ1∈θ1x|x∈X都确定了问题(3)的值,则可据此绘取最小值函数2θ1的图像,从而不难确定像集中的帕累托点与弱帕累托点,同时也得到了双目标规划问题的帕累托解与弱帕累托解.
出于求解需要,问题(3)并未完全确定双目标规划问题的像集,仅仅得到其下边界.我们还可以求解如下最大化问题以确定像集之上边界:
max θ2xs.t.θ1x=θ1,x∈X.(4)
设问题存在最优值,并记为2θ1.于是,在给定目标函数1取值θ1的情况下,我们确定了目标函数2的变动范围,有θ2∈2θ1,2θ1,从而得到双目标规划问题像集的一个大致认识.
3步骤与示例
综上,为确定双目标规划问题(1)的像集及弱帕累托解集,其基本步骤可细分为如下三步:首先,确定目标函数θ1x在可行解集X上的值域;其次,针对目标函数θ1x在其值域中的所有取值θ1,求单目标规划问题(3)与(4)的最优解,以确定双目标规划问题像集的下边界与上边界;最后,根据问题(3)的拉格朗日乘子符号,判断可行解是否为双目标规划问题的局部弱帕累托解.当然,视问题不同可将两个目标函数的主次关系进行相应调整,即,也可在给定目标函数θ2x取值基础上探讨目标函数θ1x的取值范围.
第二步要求针对某一目标函数的所有可能取值去确定另一个目标函数的最大值与最小值,事实上已将双目标规划问题转化为单目标规划问题.在数值解法之余,有时亦可确定一个目标函数的最大、最小值相应于另一个目标函数具体取值的函数关系式.
4 经济学应用
经济学往往面临价值取向的二维性.经济人总是权衡成本与收益,就生产者而言,产出最大而投入最小;就消费者而言,效用最大而支付最小;就投资者而言,收益最大而风险最小,等等,都是经济人理所当然的考虑.事实上,经济学研究源于资源的稀缺性,经济决策的核心是优化稀缺资源的配置与利用,其中不乏经典的双目标规划问题,也采用了类似的处理方式.
比如,微观经济学中生产函数与成本函数的定义.任何生产总是涉及到投入与产出两类目标,问题的像集表现为生产可能集.具有帕累托特征或弱帕累托特征的生产方式需具备如下条件:给定投入的情况下,获得最大的产出;或者,在给定产出的情况下,投入成本最小.这两个条件分别定义了生产函数与成本函数,事实上确定了生产可能集的部分边界.显然,这一机理与确定像集边界一致.
又比如,金融经济学中资产组合前沿边界的确定事实上即等价于双目标规划问题像集的确定,其决策变量为资产组合权重向量,两个目标函数分别是资产组合权重的方差函数与期望收益函数.问题的经典处理方式即Harry Markowitz (1952)提出的均值-方差模型[11]采用了双目标规划像集求解方法,即,在给定期望收益的前提下考察方差的最小值,或者,在给定方差的前提下谋求期望收益的最大值.处理结果的表现方式亦然,得到了双目标规划问题像集的上下边界,也就是资产组合前沿边界.
5 结论
利用像集探究多目标规划问题的帕累托解与弱帕累托解是一种传统思路,当问题为双目标规划类型时,尤具可行性.从确定双目标规划问题的像集边界入手,以拉格朗日乘子符号或像集边界函数单调性求取问题的局部弱帕累托解,这提供了双目标规划问题的一个分析框架.必须承认,囿于作者学识,此处仅提出一个分析框架,相关结论并未给出严格的数学证明,不过,该分析框架确实具有较好的应用前景.
参考文献
[1]杨轶华, 吕显瑞, 刘庆怀等. 求双目标凸规划问题有效解集的内点同伦算法[J]. 吉林大学学报, 2006, 44 (1): 39-43.
[2]刘庆怀, 林正华. 求解多目标规划最小弱有效解的同伦内点方法[J]. 应用数学学报, 2000, 23 (2): 188-195.
[3]于丽英, 杨雷. 生产计划的双目标混合整数规划模型及其求解[J]. 上海交通大学学报, 2001, 35 (7): 1100-1102.
[4]王兆杰, 高峰, 翟桥柱等. 高耗能企业关口平衡问题的双目标规划模型[J]. 西安交通大学学报, 2013, 47 (8): 26-32.
[5]张人千, 张兰慷. 基于收益-风险双目标规划的随机能力扩张模型[J]. 系统工程理论与实践, 2015, 35 (7): 1678-1688.
[6]杜进有, 谢汶莉. 城市群环路的双目标规划模型[J]. 西南交通大学学报, 2006, 41 (1): 102-106.
[7]隽海民, 裴玉龙, 申翔浩. 城市客运交通结构生态效用双目标优化模型[J]. 公路交通科技, 2012, 29 (7): 139-143.
[8]曾玉华, 彭拯. 一种求解双目标规划的非精确交替方向法[J]. 运筹学学报, 2010, 14 (4): 121-128.
[9]魏权龄. 经济与管理中的数学规划[M]. 北京: 中国人民大学出版社, 2011.
[10]Paul Milgrom, Ilya Segal. Envelope Theorem for Arbitrary Choice Sets [J]. Econometrica, 2002, 70 (2): 583-601.
[11]Harry Markowitz. Portfolio Selection [J]. Journal of Finance, 1952, 7 (1): 77-91.
[12]林锉云, 董加礼. 多目标优化的方法与理论[M]. 长春: 吉林教育出版社, 1992.
[13]胡毓达. 多目标规划有效性理论[M]. 上海: 上海科学技术出版社, 1994.
