快递企业末端共同配送联盟利益分配研究——基于改进的Shapley值法

李　赫

(安徽财经大学 工商管理学院，安徽　蚌埠　233030)



快递企业末端共同配送联盟利益分配研究
——基于改进的Shapley值法

李赫

(安徽财经大学 工商管理学院，安徽蚌埠233030)

文章从静态和动态两个方面，综合考虑联盟利益分配的风险因素、服务质量因素、入盟时间因素和核心竞争力因素，改进Shapley值法，旨在探索实现末端共同配送联盟利益公平分配的方法，促进快递企业末端共同配送联盟的可持续发展。

快递企业；末端共同配送联盟；Shapley值法；利益分配

一、引　言

近年来随着电子商务的不断发展，我国快递业市场需求激增。一方面随着外资快递企业的入驻及国有快递改革和民营快递的壮大，我国快递市场竞争日益激烈；另一方面快递末端配送紧贴消费者，消费者感知到的配送服务的时效性和便捷性直接影响快递企业市场地位。现阶段由于单个快递企业配送能力和服务区域的局限性，使得企业难以在抵御市场风险的同时满足消费者繁多的服务需求。因此，快递企业间结成末端共同配送联盟是解决末端配送问题、适应市场竞争和更好地服务消费者的必然趋势。

快递末端共同配送联盟是物流联盟的一种形式。它是指多个快递企业，在物流配送的末端环节，采用共同配送的模式，坚持共同的经营理念，结成优势互补，风险共担，收益共享的统一联盟体。其所具有的集约化特点，能够有效整合和利用配送资源，弥补配送能力的不足，同时规避企业单独运营的风险。[1]共同配送联盟优势具体表现为通过成员共同协作，扩大配送市场份额，提高联盟配送效率，优化联盟配送服务，降低配送成本，从而增加联盟配送收益，提升快递业竞争力。然而，随着市场竞争的加剧，联盟成员间逐步演化为合作与竞争的关系，快递企业间既需强化协作增加共同收益，又要维护企业自身利益和竞争优势。利益作为成员加入联盟的诱导因素，其分配的公平与合理性对于调动成员的合作积极性，协调成员间的关系，维持联盟稳定和可持续发展，实现整体和个体的双优化具有重要的意义。

二、利益分配研究述评

现阶段关于企业联盟利益分配问题，大多采用博弈论对其进行研究。曹巍等(2015)[2]。研究快递企业、物流企业和便利店三方合作的物流模式，得出Shapley值法是一种相对公平的利润分配方法。魏学成(2010)[3]考虑了供应链中成员的风险系数，并运用模糊综合评价法改进传统的Shapley值法，实现供应链联盟利益分配的合理化。对绿色供应链的利益分配方法进行改进时，在考虑风险因素的同时，还需进一步考虑各成员的投入因素和努力程度(穆慧萍等，2013)[4]。栾东庆等(2013)[5]从服务供应链利益来源的角度出发，运用eSCM-SP(服务提供商外包能力模型)优化传统的服务供应链利益分配机制。王永明等(2014)[6]基于鲜活农产品的特性，通过损耗控制、质量安全、准时性等多因素修正Shapley值法，并运用组合权重法综合确定修正系数，解决农产品三级供应链利益分配问题。张玉春等(2014)[7]结合果蔬农产品配送联盟特点，对联盟中的配送企业和零售商企业，分别根据入盟时间和配送距离进行传统Shapley值法修正，实现联盟利益分配的公平合理。吕萍等(2011)[8]构建了包含激励因素的总承包商与分包商间的利益分配模型，以Shapley值法为基础，综合考虑成员间风险差异与创新对供应链核心竞争力提升的积极作用，使得供应链的利益分配趋于合理化。

上述文献基本都考虑了Shaply值法的不足，并结合各行业情况，综合考虑利益分配主体间风险和资源投入等差异，对Shapley值法实施修正，保证利益分配的有效性和合理性。但现有研究仅静态的对现有整体利益进行公平分配，没有将利益分配与整体价值增值动态联系起来，借助利益分配促进整体和个体利益持续最大化，实现整体可持续发展。本文基于电子商务环境下，快递企业末端共同配送联盟的不断兴起，研究联盟利益分配问题。在Shapley值法的基础上，结合风险和服务质量因素实现静态环境下联盟利益分配优化，并动态的考虑联盟内企业的入盟时间和核心竞争力对现有收益和未来收益取得的影响，保证动态环境下联盟的可持续发展。

三、快递企业末端共同配送联盟利益分配

(一)利益分配的基本原则

公平公正的利益分配是共同配送联盟存在和壮大的关键，合理的利益分配，能够协调联盟成员间关系，调动联盟成员共同协作的积极性，同时增强彼此间信任。由于市场环境的可变性，因此末端配送联盟应遵循利益分配的基本原则，提升联盟的市场适应性和竞争力。

1.平等共存，互帮互惠原则

末端共同配送联盟中的每个成员都是联盟不可或缺的组成部分。联盟内成员实力参差不齐，但都渴望通过协作增加共同利益，同时借鉴同行业经验，提升自身市场竞争力。联盟的壮大和发展，不能仅依靠哪一个企业。因此联盟利益分配过程中，需平等对待每个成员，在保证良好的合作关系的基础上，综合考虑每个成员的状况，给予其生存和发展所需财力。

2.风险、投入与收益成正比

利益分配过程中，快递企业为联盟所付出的努力和承担的风险应与其所分得的收益匹配。成员的付出和回报成正比是调动成员协作积极性，维护联盟合作关系的基本保障。

3.动态与静态相结合原则

联盟利益分配方案是协调联盟成员间关系和贯彻联盟发展战略的有效途径。因此，需用发展的眼光去看待利益分配问题，在动态考虑成员过去的投入对现有收益影响的同时，将静态与动态相结合，注重现有收益的分配与未来收益取得间的关系，实现联盟稳定、持久的发展。

(二)利益分配的影响因素

收益是联盟成员为联盟做出贡献所获得的回报。结合快递企业的服务特点和末端共同配送联盟利益分配的基本原则，快递企业在利益分配时应考虑风险、入盟时间、末端配送服务质量和快递企业核心竞争力对合作收益取得的影响。

联盟内快递企业因承担的配送区域、服务对象和配送要求的不同，所面临的风险也不同。快递企业的风险包括外部风险、业务风险和自身风险[9]。风险越大，企业遭受损失的可能性就越大，同时应获得的收益更多。因此利益分配过程中考虑风险因素，能够鼓舞成员勇于面对风险，使分配更加公平合理[10]。

末端共同配送服务质量是影响利益分配的核心要素，也是取得收益的重要保障。末端配送直接服务于消费者，优质的配送服务是联盟赖以生存的基础。电子商务环境下，消费者对服务质量的满意程度，不仅关乎联盟市场配送份额和形象，更关乎电子商务企业的形象和消费者的体验。利益分配时考虑末端配送服务质量的因素，有助于激励联盟成员注重提升服务质量，巩固联盟实力，为联盟的稳定和发展奠定基础。

入盟时间也是利益分配时应考虑的因素之一。联盟建立初期，资金、设施和设备短缺。此刻加入的快递企业相比较此后加入的企业，需要付出更多的沉没成本和努力，承担更多的风险。基于货币时间价值和固定资产累计折旧的考虑，初期入盟的企业投入相同的资源要比此后的企业对联盟共同收益的取得助力更大。因此，利益分配时动态的考虑入盟时间对现有收益分配的影响，既有利于坚定初期入盟者继续留下的决心和维护已入盟者对联盟的信任，也有利于吸引更多有实力的快递企业尽早加入联盟。

快递企业核心竞争力是快递末端共同配送联盟的灵魂。整体的可持续发展是个体可持续发展的前提，但任何一个整体的永续存在不能仅仅考虑眼前的得失，需要用发展的眼光去处理利益分配问题。激烈的市场竞争中，快递企业核心竞争力可以帮助联盟适应市场竞争环境，满足消费者日益增加的个性化配送需求，寻求联盟持久发展的动力[11]。因此利益分配过程中动态的考虑快递企业核心竞争力，可以促进联盟成员加大对自身核心竞争力的培养，提升联盟抵御市场风险的能力，寻求联盟和快递企业个体可持续发展。

四、Shapley值法分配策略

(一) 快递企业末端配送联盟合作博弈模型

1.快递企业集合

在末端配送过程中，有n个快递企业参与联盟I，则I={1,2,3...,n}。

2. 特征函数

对于n个快递企业随机的一种集合S⊆I都对应着一个实数值v(s),v(s)表示i个快递企业在实施末端共同配送后的总收益。

当v(s)满足以下三个条件时，则称集合[I,v]为n个快递企业间的合作博弈，v为博弈的特征函数。

(1) v(ø)=0即当末端共同配送联盟中的快递企业都不愿意合作时，整体收益为0。

用中国苏州纽迈电子科技有限公司生产的MesoMR23-060H-I核磁共振分析仪测定。该仪器的共振频率为23.4033 MHz，磁体强度为0.5 T，线圈直径为60 mm，磁体温度为32℃。

(2) v(S1∪S2)v(S1)+v(S2)

条件 (2)和(3)表明联盟获得的收益一定大于快递企业单独运营时收益之和。

(二)Shapley值法公理

保证收益分配的公正是合作继续进行的基石，但各快递企业合作博弈问题有很多解，Shapley值三公理是寻求最优解的有效途径。

公理一：快递企业从联盟中分配的利润与其被标注的记号无关。

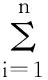
公理三：快递企业同时参加两项合作时，分配的总报酬分别为两项合作之和，即φi(U+V)=φi(U)+φi(V)。

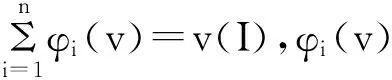
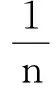
五、Shapley值法的改进

(一)考虑风险(Risk)因素的Shapley值修正算法

(二)考虑末端配送服务质量(The end of the distribution service quality) 因素的Shapley值修正算法

末端共同配送服务质量是联盟主营业务实力的直接体现，消费者对配送服务质量的满意程度直接决定了联盟收益的大小，因而利益分配中考虑配送服务质量因素，是保障分配合理与有效的基础。

(三)考虑入盟时间(Entry time)因素的Shapley值修正算法

早期的入盟者相较于后期的入盟者，为联盟的建设承担了更多的风险和付出了更多的努力。动态的考虑入盟时间对利益分配的影响，能够防止联盟成员的流失并吸引更多入盟者，有利于联盟良性发展。

(四)考虑快递企业核心竞争力(Express delivery enterprise core competitiveness)因素的Shapley值修正算法

(五)综合考虑上述因素

六、算例分析

假设甲、乙、丙三家快递企业组成末端共同配送联盟，若三者独立经营，则各自获利情况分别为8万元，6万元和2万元。若甲与乙合作，获利为18万元；甲与丙合作，获利为14万元；乙与丙合作，获利为10万元；甲、乙、丙共同合作时，获利为20万元。各项假设如表1。

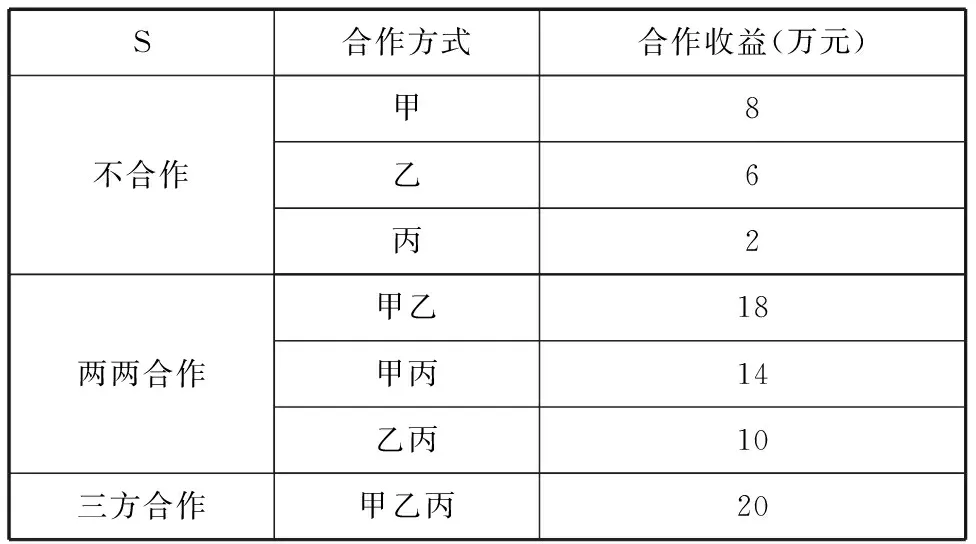
表1　快递企业末端共同配送联盟收益情况

由表1可知，快递企业通过合作结成联盟比不合作更加有利于单个企业收益的增加。

(一)Shapley值法

根据Shapley值法计算出快递企业甲应分配的收益见表2。

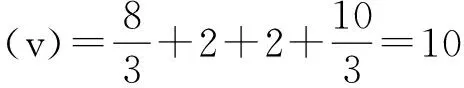
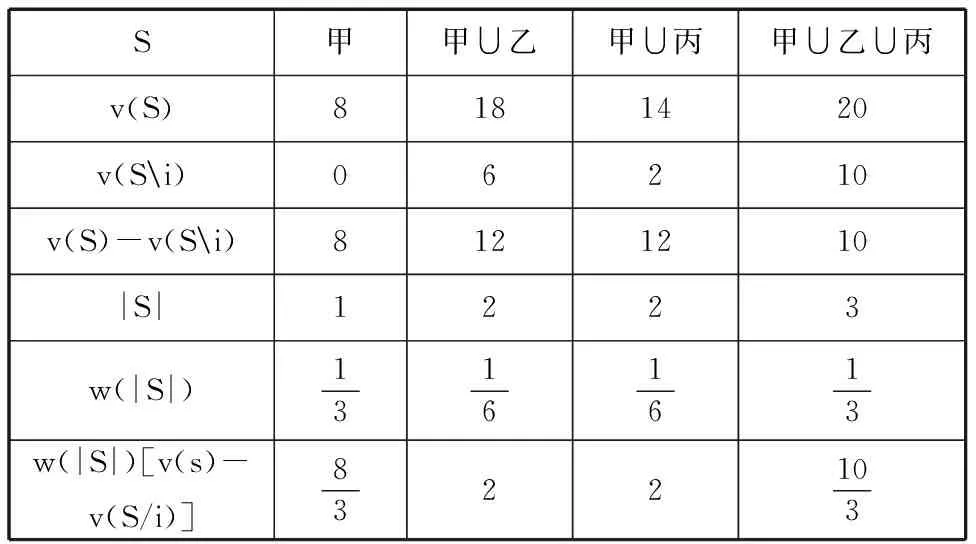
表2　快递企业甲分得的收益

(二)改进的Shapley值法

假设快递企业甲、乙和丙承担的风险系数分别为30%、30%和40%。考虑风险因素修正后的联盟收益分配如表3。联盟中丙所承担的风险最大，大于平均风险，风险修正因子大于0，因此丙有权利多分配些收益。

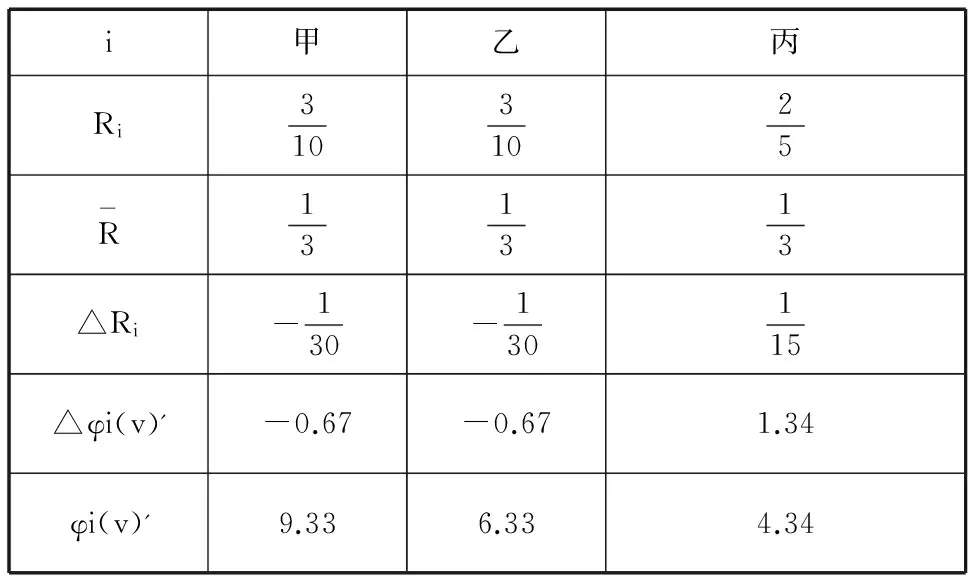
表3　考虑风险修正因子的利益分配

假设快递配送行业最优质的服务质量为100分，快递企业甲、乙和丙末端配送服务质量分别为90分、84分和81分。则考虑末端配送服务质量因素修正后的联盟收益分配如表4。联盟成员中，甲的末端配送服务质量高于联盟平均水平，较接近于行业领先水平，末端配送服务质量修正因子大于0。联盟利益分配时，应多分配些收益激励甲继续保持良好的服务质量，同时通过收益分配的减少，提醒乙和丙向甲学习。

表4　考虑末端配送服务质量修正因子的利益分配

假设快递企业甲、乙和丙入盟时间分别为90、93和105个月，则考虑入盟时间因素修正后的联盟收益分配如表5。联盟成员中丙入盟较早，其入盟时间修正因子大于0，考虑入盟时间因素后，其分配利益会有所增加。甲和乙相较于丙，入盟时间略晚，考虑入盟时间修正后，其所得收益有所减少，但是若甲和乙继续保持参加联盟的决心，随着联盟的持续存在和不断壮大，甲和乙的这种状况会逐步消失。

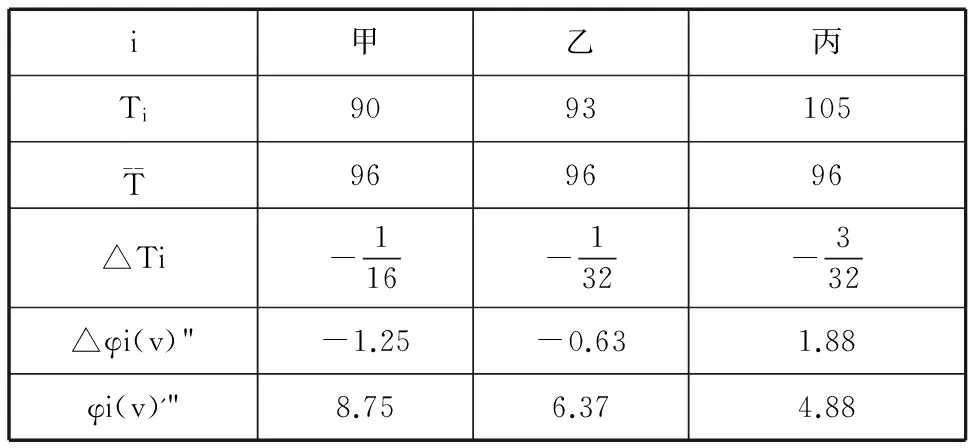
表5　考虑入盟时间修正因子的利益分配

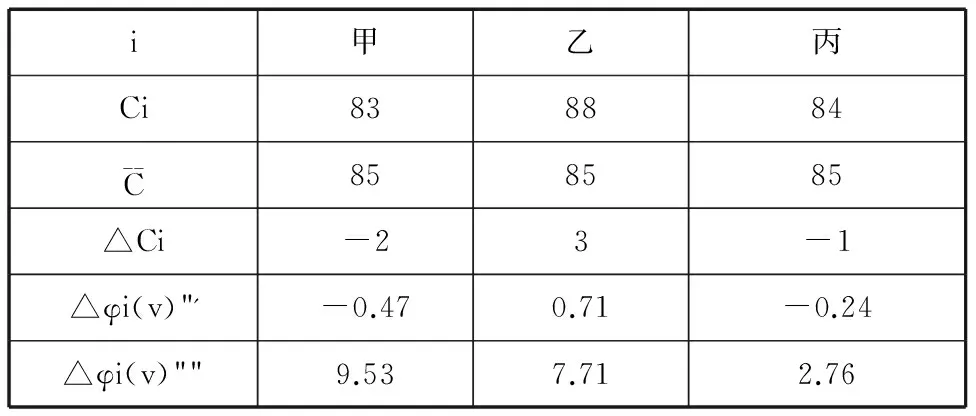
假设快递行业最强的核心竞争力为100分，联盟中快递企业甲、乙和丙分别为83、88和84分，则考虑快递企业核心竞争力因素修正后的联盟收益分配如表6。联盟中乙企业核心竞争力最接近于行业最强核心竞争力，企业核心竞争力修正因子大于0，其对联盟持续发展具有深远的影响。因此考虑核心竞争力因素，分配乙更多收益，鼓励其继续提升企业实力，同时督促甲和丙对核心竞争力的提升付出更多的努力。

表6考虑快递企业核心竞争力修正因子的利益分配

i甲乙丙Ci838884C__858585△Ci-23-1△φi(v)"'-0.470.71-0.24△φi(v)""9.537.712.76

综合考虑以上四种因素，运用AHP法得出快递末端共同配送利益分配影响因素的权重向量λ=[0.25,0.25,0.25,0.25]，则得出快递企业甲乙和丙最终分配的收益为：

φ甲(v)＾=λ1φ甲(v)'+λ2φ甲(v)"+λ3φ甲(v)"'+λ4φ甲(v)""=9.70万元

φ乙(v)＾=λ1φ乙(v)'+λ2φ乙(v)"+λ3φ乙(v)"'+λ4φ乙(v)""=6.79万元

φ丙(v)＾=λ1φ丙(v)'+λ2φ丙(v)"+λ3φ丙(v)"'+λ4φ丙(v)""=3.51万元

上述计算结果表明，综合考虑四种因素后改进的Shapley值法与仅考联盟成员贡献的Shapley值法相比，联盟内快递企业获得的收益有所差别。因为考虑多因素对利益分配机制的调整可以更加公平合理的分配共同利润，增加联盟成员间的信任和增强协作关系，确保快递企业利润最大化和联盟可持续发展。

七、结　论

对于快递企业之间的利益分配，组建联盟前后和Shapley值改进前后的对比如表7所示。

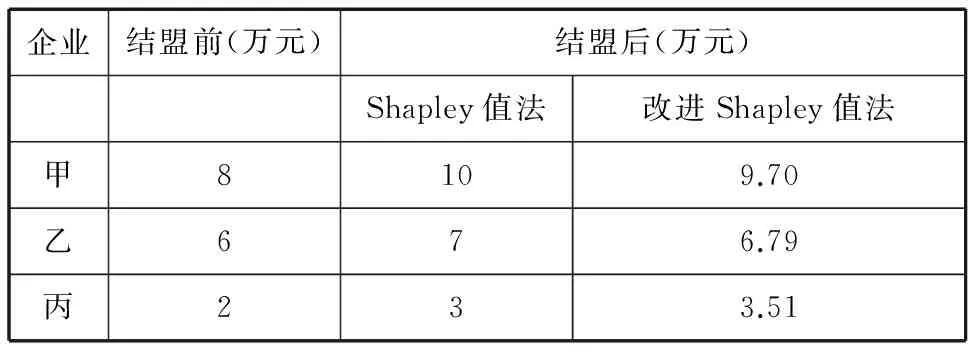
表7　快递企业结盟前后利益对比

可见，结盟后，每个快递企业的收益都比单独运营时收益有所增加，在仅仅考虑贡献因素的条件下，甲企业的收益最大。但在联盟可持续发展目标下，综合考虑风险、配送服务质量、入盟时间和快递企业核心竞争力因素，丙企业由于承担的风险较大，入盟时间较长，快递企业核心竞争力较强，使其相比之前获得更多的收益。

电子商务环境下，快递市场竞争日趋激烈。消费者服务要求日益提高，因此快递企业结成联盟共同完成末端配送任务，是扩大配送市场，保障配送服务质量，提升配送能力的必然趋势。与此同时，联盟的利益分配也是影响成员间合作意愿，协调合作关系和达成合作目的的关键。合理而公正的分配能够有效调动成员积极性，实现联盟整体和个体利益的最大化，保证联盟可持续发展。Shapley值法在现有收益的分配中，仅仅考虑了快递企业对联盟的贡献，是静态的理论意义上的“公平”与“合理”。但联盟是一个动态变化的过程，现有的利益分配策略作为联盟战略的一部分，对联盟未来收益的取得和规模的不断壮大具有积极的影响，因此在对Shapley值法改进时，不仅应静态的考虑现有收益分配的优化，还应动态考虑利益分配对联盟未来战略实现的影响。

本文引入风险因素、快递末端配送服务质量因素、入盟时间因素和快递企业核心竞争力因素，构建改进的Shapley值法分配模型，算例表明这种方法是有效且合理的，优势表现为：首先，静态的考虑风险因素和快递末端配送服务质量对现有收益取得的影响，所承担的风险系数越大，配送服务质量越好，获得收益越多，体现风险、投入与收入成正比的原则。其次动态考虑入盟时间和快递企业核心竞争力对联盟收益持续取得的影响，对坚定成员入盟决心和不断寻求自身进步，具有一定的激励作用。最后，修正后的分配方案更加符合快递企业末端共同配送联盟的实际情况，解决了利益分配中的矛盾，有助于保证利益分配稳定性和合理性。

[1]吕庆敏，李美燕.快递企业共同配送流程服务质量优化研究[J].商场现代化，2014，(21)：62-64.

[2]曹巍,刘南.终端网点参与下电子商务物流外包的协调策略研究[J].管理工程学报,2015,29(4):194-203.[3]魏学成,李文涛.基于改进Shapley值法的供应链联盟利益分配研究[J].统计与决策,2010,(23):53-55.

[4]穆慧萍,郜红虎,曹飞.基于Shapley值修正的绿色供应链系统利益分配策略研究[J].物流技术,2014,33(1):280-282.

[5]栾东庆,吴忠,夏志杰.基于改进Shapley值法的服务供应链利益分配研究[J].物流技术,2014,33(6):249-251.

[6]王永明,蒋家忠,苏文彬.鲜活农产品供应链的收益分配研究——基于Shapley值法和组合权重法[J].物流商论,2014,(09):156-157.

[7]张玉春,周金华,申风平,任小洋.基于Shapley值法的果蔬农产品配送联盟的利益分配[J].生产力研究,2014,(11):50-52.

[8]吕萍,张云,慕芬芳.总承包商和分包商供应链利益分配研究——基于改进的Shapley值法[J].运筹与管理,2012,21,(6):211-216.

[9]陈平,快递末端物流配送的风险分析与防范措施研究——以申通快递为例[J].物流工程与管理,2013,35(6):53-57.

[10]杨从明,朱海彬,任晓冬.基于Shapley值法的矿产资源开发利益相关者利益分配博弈分析[J].地球与环境,2014,42,(3):424-429.

[11]王莲花,牟丹凤.基于层次分析法的民营快递企业竞争力模糊综合评价研究[J].物流技术,2013,32(7):163-165.

责任编校：陈强，王彩红

Study on Revenue Allocation Strategy of the End Joint Distribution of Express Delivery Enterprises

LI He

(School of Business Administration,Anhui University of Finance & Economics,Bengbu 233030,China)

In this paper, on the basis of current studies on application of Shapley value method in revenue allocation, we further research the revenue allocation mechanism of the end joint distribution of express delivery enterprises.From two aspects of static and dynamic, we considered comprehensively the factors influencing the revenue allocation of the end joint distribution of express delivery enterprises and modified the Shapley value method. It helps alliance explore the fair revenue allocation strategy and promote the sustainable development of alliance.

express delivery enterprises; end joint distribution alliance; Shapley value; revenue allocation

2016-03-24

安徽财经大学研究生科研创新基金项目(ACYC2015132)

李赫，女，安徽芜湖人，硕士，研究方向为物流与供应链管理。

F253

A

1007-9734(2016)04-0071-07

DOI:10.19327/j.cnki.zuaxb.1007-9734.2016.04.012