基于描述函数法的航天器非储能喷气控制器分析与设计*

邓 雅 张锦江 马艳红,2 蔡 彪

1.北京控制工程研究所, 北京100190 2.空间智能控制技术重点实验室, 北京100190



基于描述函数法的航天器非储能喷气控制器分析与设计*

邓 雅1张锦江1马艳红1,2蔡 彪1

1.北京控制工程研究所, 北京100190 2.空间智能控制技术重点实验室, 北京100190

针对航天器喷气发动机模拟式控制器中的非储能型非线性控制系统进行分析设计。以Schmitt触发器环节为例，基于描述函数法计算极限环交点，并利用系统稳态输出，得到稳态极限环特性，计算描述函数意义下极限环频率误差界，给出控制器参数整定方法。通过仿真实例验证该方法通用、有效，为工程应用提供参考。 关键词 喷气控制; 描述函数法; 非线性环节; Nyquist图

作为航天器上重要的执行机构之一，喷气发动机(或称推力器)能够提供较大的控制力矩，但通常只有开和关两种状态，使得控制输出不连续，是一类典型的非线性系统，其控制器的分析和设计存在较大难度。

按照喷气控制器的类别，可分为模拟式控制器与数字式控制器[1]。其中模拟式控制器主要以Schmitt触发器为基本组件，附加校正环节，结构简单，性能可靠，可采用模拟电路实现，是早期航天器控制的主要实现方式。在此基础上，依据附加校正环节的不同，通常有PWPF(Pulse-Width Pulse-Frequency)调制器、PRM(Pseudo-rate Modulator)调制器等[2]。文献[3]给出几类调制器的结构及静态特性，所得结果可以为控制器的设计提供参考。数字计算机出现后，数字式控制器应运而生，例如相平面控制器[4-5]，效率提升的同时也增加了复杂程度。文献[6-9]分别给出了航天飞机和国际空间站俄罗斯舱段的反作用喷气相平面控制系统结构。然而，无论是模拟式还是数字式控制器均不可避免地引入了非线性环节，工程上处理非线性的一个重要方法是描述函数法，也称谐波平衡法，由P. J. Daniel于1940年首先提出。文献[10-12]介绍了NASA开发的基于描述函数法的INCA (Interactive Controls Analysis)软件，该软件基于描述函数的定义，给出了描述函数的数值辨识方法，可以用来辅助带挠性附件航天器的喷气控制系统的分析和设计。文献[13]基于描述函数的数值辨识，分析相平面喷气控制器的稳定性并评估稳定裕度。

由于计算的复杂性，目前针对基于描述函数法的研究大多局限于定性分析，设计上仍依靠经验试凑法，急需一种更加精确实用的分析和设计方法。

本文考虑模拟式喷气控制器，以Schmitt触发器构成的系统为例，对非储能型非线性控制系统进行分析设计。计算描述函数意义下的极限环交点，分析极限环稳态特性。继而分析极限环频率误差，给出控制器参数调整方法。最后通过仿真实例进行验证，该方法具有通用性，能够为工程应用提供参考。

1 描述函数法

图1为典型非线性系统框图，其中G(s)为系统的线性环节，具有低通滤波特性，N(A)为系统的非线性环节。对于非储能型的非线性环节，其描述函数是输入正弦信号幅值为A的函数[14]，记为N(A)。

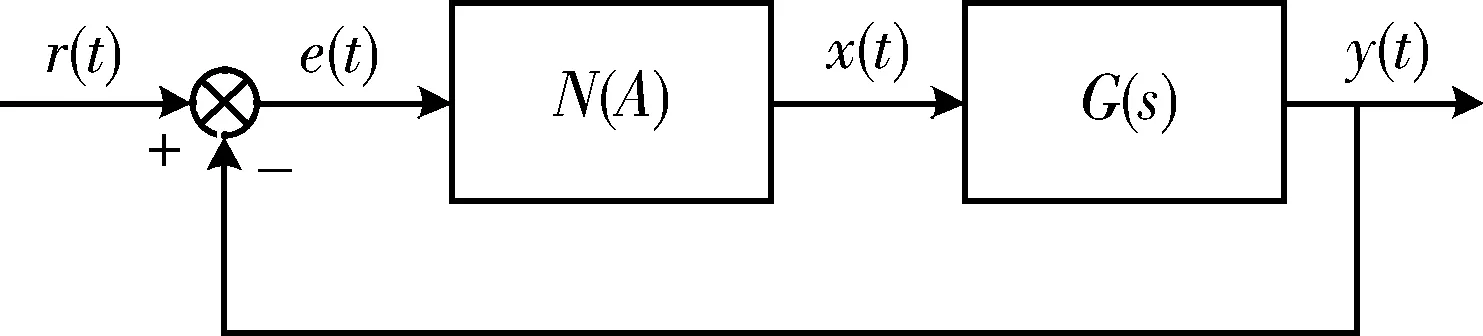
图1 非线性系统框图

该闭环系统的稳定性分析采用将-1/N(A)和G(jω)绘制在同一个Nyquist图中，若G(jω)曲线不包围-1/N(A)曲线，则非线性系统稳定；若包围，则不稳定；若存在交点，则可能形成极限环，需要进一步根据运动方向分析稳定性[14]。根据系统特征方程

N(A)G(jω)+1=0

产生极限环的条件为

(1)

2 以Schmitt触发器为例的非储能非线性环节描述函数分析和设计

Schmitt触发器是构成模拟式喷气控制器的重要元素，具有典型的非储能型非线性特性，根据前述基于描述函数法的分析和设计流程，本节以Schmitt触发器构成的控制系统为例进行分析。

2.1Schmitt触发器控制系统结构

Schmitt触发器为带有死区和滞环的典型非储能非线性环节，结构形式如图 2所示，其中，uon和uoff分别为Schmitt触发器的开门限和关门限电压，ui和uc分别为输入和输出电压，输入输出函数关系[1]见式(2)。

图2 Schmitt触发器

(2)

由Schmitt触发器及带有速度反馈的超前校正网络构成的系统结构如图3所示。

图3 带有Schmitt触发器的航天器控制系统

其中，I为航天器惯量，u为Schmitt触发器输出，Tc为额定控制力矩，τ为速率反馈增益。输入θr为期望姿态角度，输出θ为实际姿态角度。

2.2 基于描述函数的频域特性分析

首先将Schmitt触发器构成的控制系统变换为图 1所示的标准形式，系统回路中线性部分

(3)

非线性部分为Schmitt触发器，其描述函数具有解析表达式[14]

(4)

定义

huon-uoff

针对该系统，给出描述函数意义下极限环交点的解析表达式。

定理1 考虑如图3所示的系统，其描述函数意义下的极限环交点为SDF(ADF,ωDF)

(5)

(6)

其中，ΔDF

ωDF为极限环频率，ADF为极限环幅值，即姿态角稳态误差幅值。

(7)

(8)

联立方程组(7)的第2式和式(8)，消去ξ，可得关于ω的方程，由于ω为实数，取方程实根

其中，ΔDF

相应的极限环幅值为将ωDF代入方程组(7)的第2式解得

2.3 基于极限环分析的稳态性能计算

由于Schmitt触发器结构简单，稳态信号确定，根据文献[8]给出的结论，直接利用其稳态极限环时域特性，可以得到精确的极限环的解ST(AT,ωT)，其中AT为极限环幅值，表示姿态控制精度，ωT为极限环频率，即2π/P，P为极限环周期。

引理1 考虑如图 3所示的系统，其稳态极限环特性为

(9)

(10)

ωT为极限环频率，AT为极限环幅值。

(11)

如图4所示，其稳态极限环左右两端为抛物线，中间段为平行于横轴的直线，开关线方程在图中标出，状态运动轨迹沿实线箭头方向，ta，tb，tc，td为状态切换时刻。

联立抛物线和开关线方程，可得ta和td时刻对应开关点的纵坐标xa 2和xd 2，二者相等，可解得极限环幅值为

从而

即为姿态角速度控制精度。

将ta和td时刻对应开关点的横坐标xa1和xd1作差，由tda，tbc阶段为匀速运动，得

故极限环周期为

频率为

图4 Schmitt触发器稳态极限环示意图

2.4 基于描述函数法和极限环分析的辅助设计

在所得极限环特性基础上，描述函数法可以用来为控制器设计提供帮助，根据图 3可以分别画出线性部分和非线性环节描述函数的Nyquist图，易知该交点为稳定极限环交点。由于描述函数法为近似方法，存在一定的误差，通过比较式(5)和式(9)，可给出下面的定理。

定理2 考虑如图 3所示的系统，其在描述函数下所求得的极限环频率与频率真值存在误差，误差上界为

Δω=ωT-ωDF

误差绝对值下界为

证明 利用式(5)和式(9)计算频率误差可得

(12)

得到极限环频率误差上界。

研究误差绝对值的下界，利用Minkowski不等式的伴随不等式：若r>1，则

等号成立条件为ab…l=0。于是，

由于不等号右边均为正项，因而不存在取等式的情形。进一步化简可得

于是，

为得到适当的控制器参数，可依据以下步骤进行基于描述函数法的Schmitt触发器设计：

步骤1：将闭环系统中的线性部分整理为一个环节G(jω)；

步骤2：选取一组初始参数，根据式(5)和式(6)计算初始极限环频率ωDF和幅值ADF，在同一个Nyquist图中绘出此时的G(jω)和-1/N(A)，初始交点处的系统性能通常是可能引发共振的且不满足指标要求的；

步骤3：在初始参数处分别计算∂ω/∂uon，∂ω/∂uoff和∂ω/∂τ，得到参数调节的方向；

步骤4：根据步骤3的结果对参数进行调节和数学仿真。

该方法给出的是针对Schmitt触发器回路的设计，但具有较强的通用性，其他非储能非线性环节可采用类似的方法进行基于描述函数方法设计。

3 仿真实例

本节将针对某航天器模型，采用Schmitt触发器构成的控制回路，验证上述非储能环节的描述函数方法。

3.1 被控对象

以某带有挠性附件的航天器为例，其传递函数模型可写成：

(13)

给定模型参数如下：

α=0.15，ωa=-0.0023±0.45j，Ka=1。

3.2Schmitt触发器仿真

给定初始Schmitt触发器参数如下：

uon=0.7，uoff=0.3，τ=0.7。

根据定理1和定理2分别计算极限环频率，可得

ωT=0.4298rad/s，ωDF=0.4281rad/s。

振荡环节频率ωa=0.45rad/s，即所形成极限环的交点与振荡频率非常接近。仿真结果如图5所示。

图5 Schmitt触发器共振情形下仿真结果

通过仿真可以看出，由于极限环频率与挠性固有频率接近，引发了明显共振现象，对系统性能产生较大影响，需要通过调节参数使极限环频率远离挠性固有频率。

经计算

根据上述规则调节参数为

参数调整前后的系统Nyquist图如图6所示，在不改变稳定性的前提下，将交点向远离挠性固有频率方向移动，调整后的极限环频率为

图6 参数调整前后的系统Nyquist图

调整后仿真结果如图(7)所示。从仿真结果可以看出，将极限环频率移走后，共振现象明显减弱，稳态误差不变，系统动态性能提升。

4 结论

基于描述函数法，研究了模拟式喷气姿态控制系统的分析和设计问题。考虑能够写出解析表达式的非储能非线性环节的描述函数，以Schmitt触发器为例，联立方程，可求得其与线性环节交点的解析表达式。进一步通过时域下稳态极限环的特性，可求得极限环精确解，将二者进行比较，给出了描述函数法的误差界。在此基础上，给出了控制器参数调节步骤和依据。最后，通过仿真实例，验证了算法的有效性和实用性。

图7 Schmitt触发器非共振情形下仿真结果

本文论述的控制器分析和设计方法，具有一定的通用性，可适应大多数非储能型非线性环节的分析。同时，文中的设计准则，给出了参数调整的依据和方向，改进了以往仅依据经验的试凑，为工程应用提供了参考。

[1] 屠善澄. 卫星姿态动力学与控制[M]. 北京: 宇航出版社, 1998.

[2]NavabiM,RangrazH.ComparingOptimumOperationofPulseWidth-PulseFrequencyandPseudo-RateModulatorsinSpacecraftAttitudeControlSubsystemEmployingThruster[C]//RecentAdvancesinSpaceTechnologies.Istanbul:IEEE, 2013：625-630.

[3]AnthonyTC,WeiB,CarrollS.Pulse-ModulatedControlSynthesisforaFlexibleSpacecraft[J].JournalofGuidance,Control,andDynamics, 1990，13(6): 1014-1022.

[4]XiaXiwang,JingWuxing,LiChaoyong,GaoChangsh-

eng.Time-SharedSchemeDesignforAttitudeControlSystemDuringSpaceSeparation[J].AerospaceScienceandTechnology, 2011，15(2): 108-116.

[5]JangJW,PlummerM,BedrossianN,HallC,JacksonM.AbsoluteStabilityAnalysisofaPhasePlaneControlledSpacecraft[R].NASAM10-0025, 2010.

[6]YangL,GriffithE.Flex-ControllerInteractionDuringSpaceStationReboost[C]//ProceedingsoftheAAS/AIAAAstrodynamicsConference.SanDiego,California：AAS, 2003：1515-1531.

[7]BennettGJ,SebeliusKP,BarthAL,NguyenLH.ISSRussianSegmentMotionControlSystemOperatingStrategyduringOrbiterRepairManeuver[C]//AIAAGuidance,Navigation,andControlConferenceandExhibit.SanFrancisco,California:AIAA, 2005. 1-10.

[8]WieB.SpaceVehicleDynamicsandControl[M].AlexanderBellDrive,Reston,VA:AmericanInstituteofAeronauticsandAstronautics, 2008.

[9]KirchweyCB,SackettLL.StabilityoftheShuttleOn-OrbitFlightControlSystemforaClassofFlexiblePayloads[C]//AIAAGuidance,Navigation,andControlConference.Gatlinburg,TN:AIAA, 1983:128-141.

[10]DowningJP,BauerFH,ThorpeCJ.ASTEC:ControlsAnalysisforPersonalComputers[R].NASA90N23052, 1990.

[11]WieB,AnthonyT.AComputer-AidedApproachtoNonlinearControlSysthesis[R].NASANAS8-36224, 1988.

[12]BauerFH,DowningJP,ThorpeCJ.NewMultivariableCapabilitiesoftheINCAProgram[R].NASAN90-23049, 1990.

[13] 张国琪, 刘洁, 董文强, 何英姿.基于描述函数法的相平面喷气姿态控制的稳定性分析[J]. 空间控制技术与应用, 2015, 41(1): 15-20. (ZhangGuoqi,LiuJie,DongWenqiang,HeYingzi.StabilityAnalysisofPhase-PlaneJetAttitudesControlSystemUsingtheDescribingFunctionMethod[J].AerospaceControlandApplication, 2015,41(1): 15-20.)

[14] 胡寿松.自动控制原理[M].第五版.北京: 科学出版社, 2007.

Analysis and Design of Nonstorage Jet Controller of Spacecraft Based on Describing Function Method

Deng Ya1, Zhang Jinjiang1, Ma Yanhong1,2, Cai Biao1

1. Beijing Institute of Control Engineering, Beijing 100190, China 2. Science and Technology on Space Intelligent Control Laboratory, Beijing 100190, China

Tosolvethenonlinearelementprobleminjetcontrollerofspacevehicleactuators,describingfunctionisemployedtostudytheanalyzinganddesigningmethod.Asatypicalnonstoragenonlinearelement, Schmitttriggerisusedasanexampletogivetheanalyticalsolutionoflimitcycle.Accordingtothesteadystateoutputofthesystem,thecharacteristicsoflimitcyclearegiven.Toestimatetheaccuracyofdescribingfunction,errorboundsoffrequencyarecalculated.Atlast,themethodisverifiedfromnonlinearsimulations.

Jetcontrol;Describingfunction;Nonlinearelement; Nyquistdiagram

*空间智能控制技术重点实验室基金(9140C590107130C59211)

2015-05-21

邓 雅(1988-)，女，石家庄人，博士研究生，主要研究方向为航天器控制；张锦江(1973-)，男，黑龙江人，博士，研究员，主要研究方向为航天器控制、制导与仿真；马艳红(1980-)，女，山西人，博士，高级工程师, 主要研究方向为大型航天结构体的姿态控制和鲁棒控制；蔡 彪(1980-)，男，山西人，高级工程师，主要研究方向为航天器导航、制导与控制系统设计和集成测试。

V448

A

1006-3242(2016)01-0064-06