基于增益分配的航天器高精度指向跟踪控制

董天舒 何英姿,2

1.北京控制工程研究所，北京 100190 2.空间智能控制技术重点实验室，北京 100190



基于增益分配的航天器高精度指向跟踪控制

董天舒1何英姿1,2

1.北京控制工程研究所，北京 100190 2.空间智能控制技术重点实验室，北京 100190

研究刚体卫星的高精度大角度指向跟踪控制问题。为保证姿态描述的全局性，由修正Rodrigues参数描述相对姿态。设计PD型姿态指向跟踪控制器，可同时实现角度跟踪和角速度跟踪。为提高控制精度，同时避免控制输出进入饱和域，本文在控制器的基础上设计了增益分配律。通过数值仿真，在存在初始指向偏差和输出饱和约束条件下，控制器可实现大椭圆轨道卫星对静止轨道卫星的高精度姿态指向跟踪。当转动惯量存在常值误差时，控制器仍然适用。 关键词 姿态指向跟踪；PD型控制；增益分配

在一些空间任务中，需要航天器对合作或非合作目标进行大角度指向跟踪，例如进行监视、抓捕或者加注任务。其中难度较大的是大椭圆轨道卫星对静止轨道卫星进行姿态指向跟踪任务，在任务中卫星本体系X轴要实时指向静止轨道上的目标卫星。由于两星轨道交会时间短、视线方向变化大、变化快，卫星指向跟踪过程需要进行大角度快速机动，对控制器要求具备高精度的大角度跟踪和角速度跟踪能力。

文献[1-2]说明了非线性状态反馈控制方法能实现刚体航天器姿态rest-to-rest 型机动控制。文献[3]指出了利用期望姿态和航天器实际姿态的相对姿态建立的运动学和动力学方程，可将姿态跟踪问题转化为对相对姿态的调节问题。文献[4]给出一种基于四元数的PD型控制器，可实现角度跟踪和角速度跟踪。文献[5]针对刚体卫星受外力矩干扰时的姿态跟踪控制问题，设计了在一定条件下相对姿态可全局渐进稳定的PD型控制器。文献[6]对近地轨道小卫星的跟踪控制问题进行了研究，对输出力矩存在饱和约束，给出一个近似全局收敛的PD型姿态跟踪控制器。文献[7]针对刚体卫星，给出基于磁力矩器和单/双反作用轮的PD型姿态跟踪控制器。

本文在相对姿态运动学和动力学方程的基础上，设计了PD型姿态指向跟踪控制器，实现卫星大角度跟踪和角速度跟踪。由于控制输出存在饱和约束，本文设计了增益分配律，可在提高控制精度的同时避免控制输出进入饱和域。通过仿真表明，该控制器能实现大椭圆轨道卫星对静止轨道卫星高精度姿态指向跟踪，同时对转动惯量常值误差有很好的鲁棒性。

1 问题描述

1.1 刚体卫星姿态运动学和动力学模型

本体系下，卫星姿态运动学方程为：

(1)

其中，C为卫星本体系相对惯性系的方向余弦矩阵，ω为卫星本体相对惯性系的角速度。(·)×运算定义为：

刚体卫星姿态动力学方程为：

(2)

其中,J为转动惯量矩阵，Td为空间环境干扰力矩，uc为控制力矩。

1.2 指向跟踪期望姿态描述

与姿态跟踪不同的是，指向跟踪中的期望姿态有明确的定义。根据任务要求，跟踪卫星的本体X轴要实时指向目标卫星，首先在轨道系下定义指向方位角α和仰角β。

图1 期望姿态的定义

图1中,Ooxoyozo系为卫星的第二轨道坐标系，zo轴由卫星质心指向地心，xo轴在轨道平面内与zo轴垂直并指向卫星速度方向，yo轴与xo和zo轴右手正交并垂直于轨道平面的法线；rbt为由卫星质心指向目标卫星质心的单位向量；方位角α为rbt在xoOozo平面上的投影与xo轴的夹角，仰角β为rbt与rbt在xoOozo平面上的投影之间的夹角。

指向跟踪期望姿态可通过2次主轴转动得到，方向余弦矩阵Cro：

(3)

相对惯性系的期望角速度可表示为

(4)

其中，ωo为卫星第二轨道系相对惯性系的角速度。

1.3 相对姿态运动学和动力学模型

描述相对姿态有多种方法，例如欧拉角法、四元数法、Rodrigues参数法和修正Rodrigues参数法(MRPs)。但是，欧拉角法在姿态转角为π/2时，存在奇异点，不适用于描述相对姿态大范围变化的情况；四元数法不存在奇异点，有很好的全局性，但在SO(3)空间内不连续，可能引起unwinding现象[8]；Rodrigues参数在姿态转角为π时，存在奇异，同样不适用于描述相对姿态大范围变化的情况。MRPs是刚体姿态近似全局的最小描述方法，不存在四元数的单位约束条件，易于实现。其在姿态转角为2π时存在奇异，在实际应用中相对姿态不容易达到这一点，可认为是近似全局的，因此本文采用MRPs描述相对姿态。定义MRPs：

(5)

其中，q0，qi(i=1,2,3)为四元数参数。

方向余弦矩阵表示相对姿态，可表示为：

(6)

式中,Cbo为卫星本体系相对轨道系的方向余弦矩阵，δσ为由MRPs描述的相对姿态。根据MRPs定义，δσ与四元数[δq0,δqv]有如下关系：

(7)

式(7)等号两侧对时间求导数

(8)

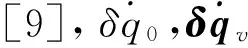
(9)

δω为航天器角速度误差，定义为：

δω=ω-Cbr(δσ)ωri

(10)

其中，ω为卫星本体相对惯性系的角速度，ωri的定义参见式(4)。

将式(7)和(9)带入式(8)，可得到相对姿态运动学方程：

(11)

式(10)等号两侧对时间求导数，有

式(12)等号两侧乘以卫星转动惯量矩阵J，再将式(2)带入式(12)，可得到相对姿态的动力学方程：

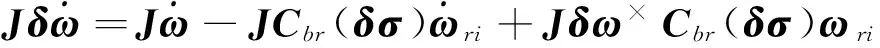
JCbr(δσ)ωri-J(Cbr(δσ)ωri)×δω-

(13)

2 姿态指向跟踪控制律设计

2.1 输出饱和约束

考虑到卫星能提供的输出力矩是有限的，为贴近实际情况，这里对控制力矩设定饱和约束条件。控制力矩uc在本体系下表述为：

(14)

其中,ucx，ucy和ucz为投影在本体系主轴上的控制力矩，统一表示为uci,i=x,y,z。

输出饱和约束可表示为：

(15)

2.2PD型控制器设计

本节设计了PD型控制器，并严格证明控制器可使相对姿态δσ和相对角速度δω渐进稳定。式(15)可见，输出力矩的饱和约束为强非线性，本节假设控制器输出是在线性域内。参考文献[4]的PD型控制器设计思路，定义中间变量ωc和ωt,

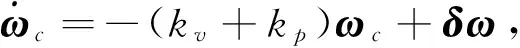
(16)

其中，kv,kp为正实数。

ωt定义为：

(17)

假设ωt满足以下条件：

(18)

为使ωt满足式(18)条件，将式(17)等号两侧乘以转动惯量J并对时间求导，有

(19)

并将式(11)和(13)带入式(19)，可得到控制律uc为

(20)

下面利用Lyapunov理论证明控制器(式(20))可使相对姿态δσ和相对角速度δω渐进稳定。选择Lyapunov函数为：

(21)

式(21)等号两侧对时间求导数，并将式(11),(17)和(18)代入，有

(22)

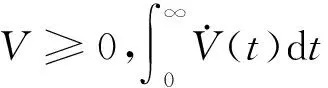
(23)

(24)

证毕。PD型控制器可使相对姿态δσ和相对角速度δω渐进稳定，说明控制器能够实现姿态指向跟踪。

3 增益分配律

当航天器指向跟踪存在初始指向偏差时，若控制器参数kp和kv的取值较大，控制输出会进入饱和域；如果控制器参数选取的数值较小，使控制输出保持在线性域内，当指向跟踪稳定后，控制器又难以敏感小角度偏差，无法实现高精度的指向跟踪。为解决这一矛盾，本文设计了增益分配律：

(25)

其中，t0，tt为增益切换时刻，(kv 0,kp0)和(kvt,kpt)分别为初始控制参数和稳态控制参数。

通过初始控制参数(kv 0,kp0)的选取，可实现初始指向误差的收敛，并且避免控制输出进入饱和域；通过稳态控制参数(kv t,kpt)的选取可实现指向跟踪进入稳态后高精度指向跟踪。增益分配律则提供了控制参数从(kv0,kp0)到(kvt,kpt)的途径，保证在参数切换过程中闭环系统稳定，同时控制输出在过程中不发生跳变，这一结论可通过仿真证明。

4 数值仿真

4.1 仿真参数

为验证控制器的有效性，利用Simulink软件搭建闭环系统，对大椭圆轨道卫星(跟踪星)指向跟踪静止轨道卫星(目标星)进行数值仿真。下面给出仿真中的关键参数。

跟踪星和目标星轨道要素如表1。

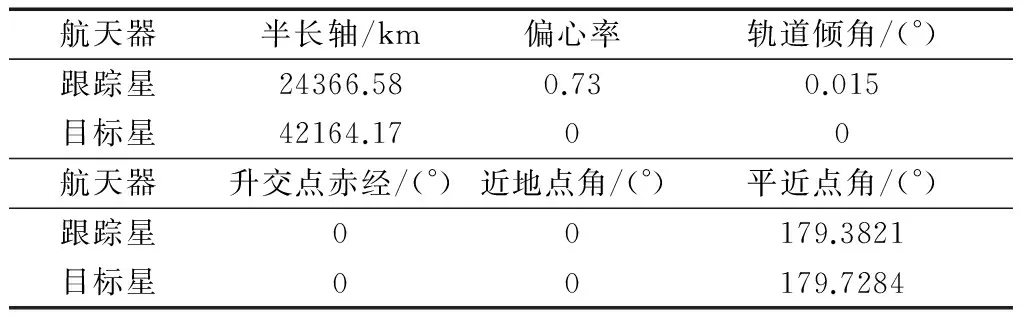
表1 卫星轨道要素

跟踪星转动惯量矩阵为：

为验证控制器的鲁棒性，设定转动惯量误差阵δJ，主轴误差取1%：

跟踪星初始角速度ω(0)设为0，初始姿态由初始指向偏差设定，初始指向偏差为：初始方位角α0=2°，初始仰角β0=1°。控制器饱和约束设定为：ucimax=60N·m,ucimin=-60N·m,i=x,y,z。

控制器参数kv与kp的对应关系见图2(a)，kv随时间的变化曲线见图2(b)。

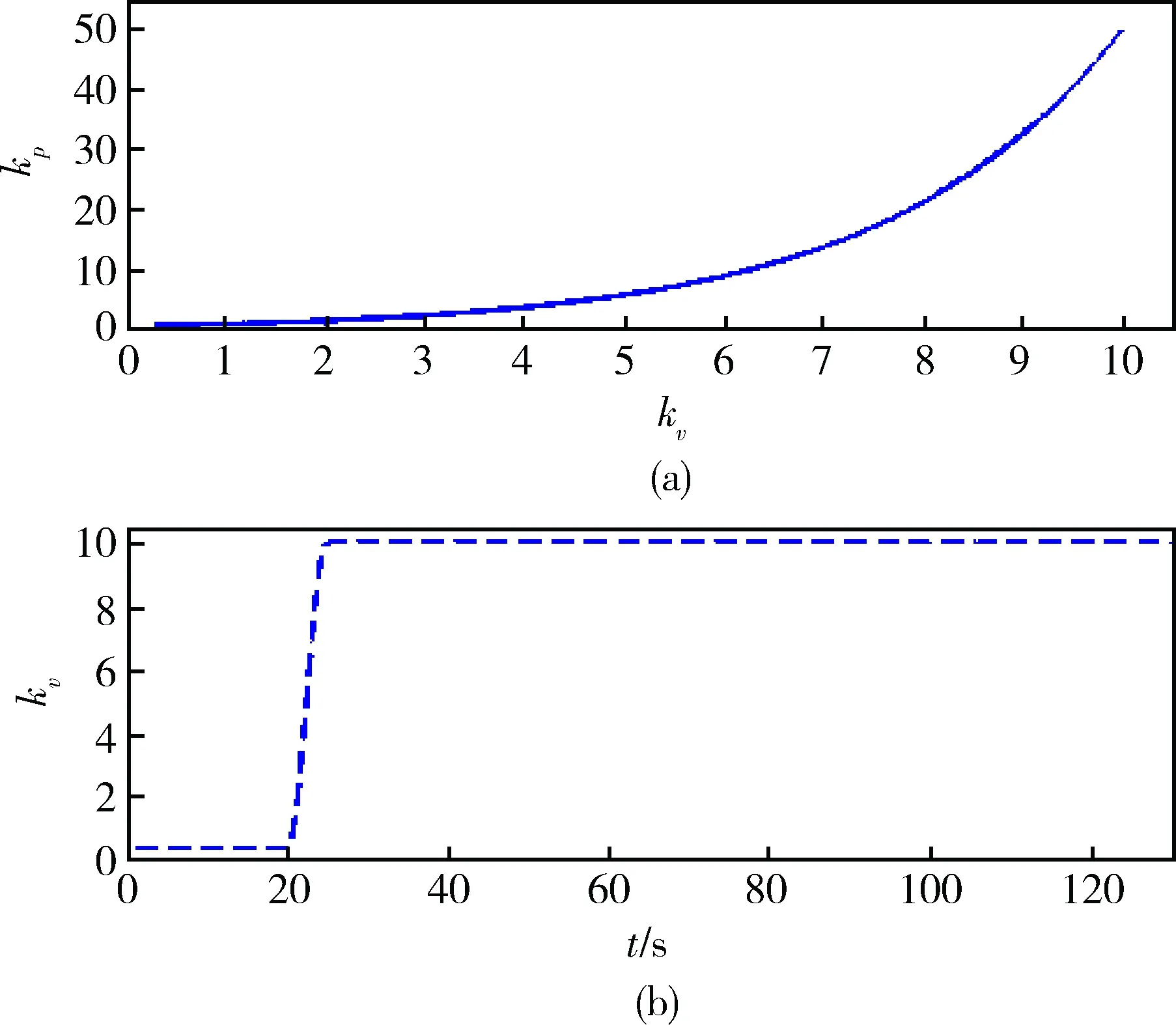
图2 控制器参数变化曲线

4.2 仿真结果及分析

仿真结果可见图3～9。图3为跟踪星与目标星相对距离随时间的变化曲线。图4为期望姿态、期望角速度曲线。从图3和4中可见两星交会时间很短，从初始时刻到两星距离10km处仅65s，整个指向跟踪过程仅130s，在整个跟踪过程中，期望姿态的变化在俯仰轴方向有范围大、变化快的特点。

图5为由修正Rodrigues参数描述的相对姿态的变化曲线。图6为相对角速度变化曲线。图7为跟踪过程中控制力矩输出曲线。由图5～7可见，存在初始指向偏差和输出饱和约束的条件下，控制器能实现大椭圆轨道卫星对静止轨道目标卫星的指向跟踪，相对姿态δσ和相对角速度δω可在20s内收敛，说明控制器具有良好的跟踪性能。通过增益分配律的设计，控制输出力矩没有进入饱和域，并且始终为平滑曲线。

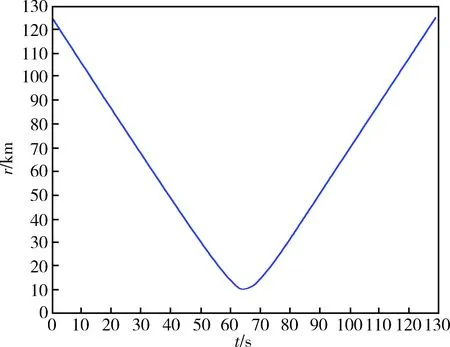
图3 大椭圆轨道卫星与目标星相对距离曲线

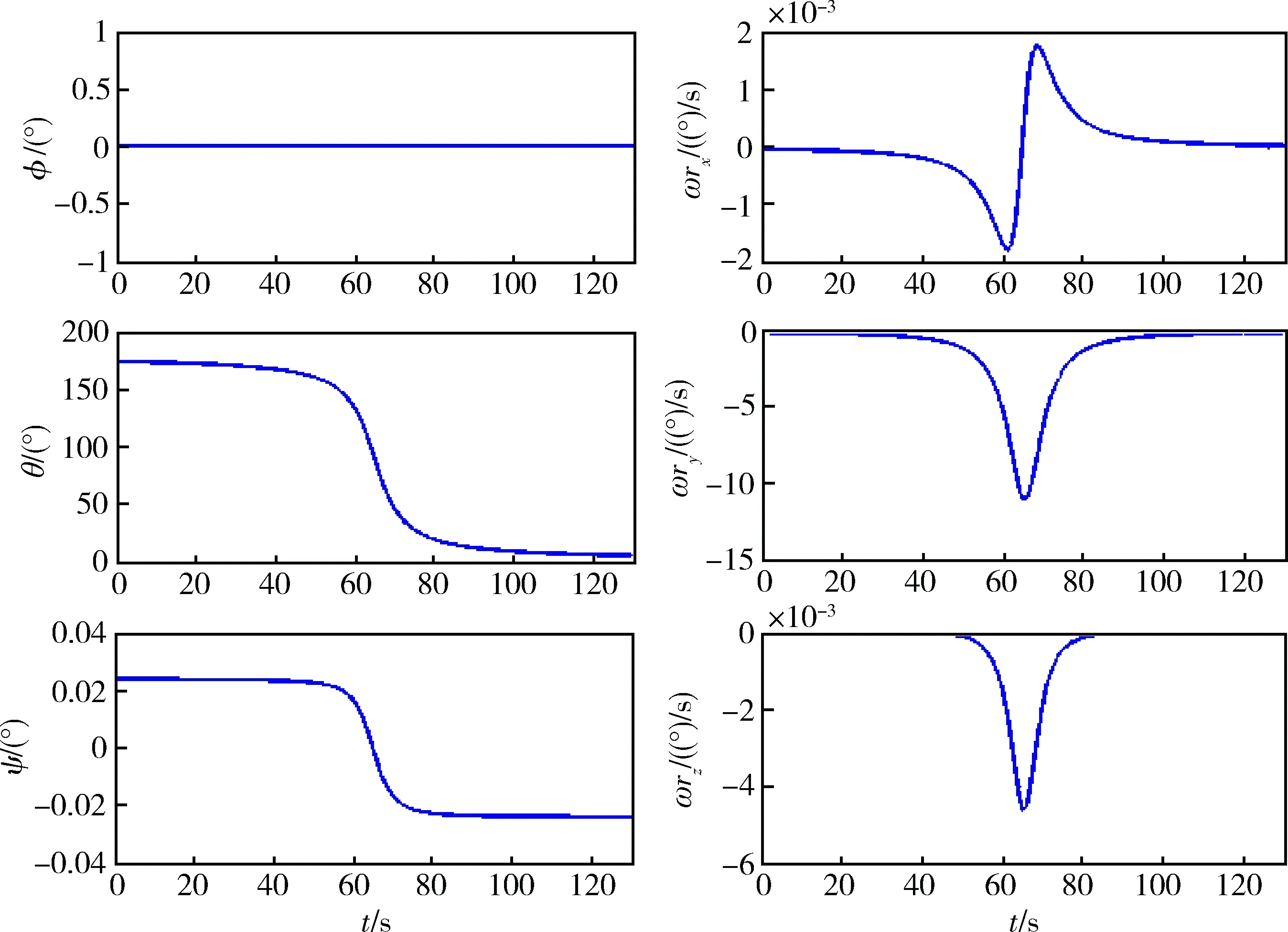
图4 期望姿态及期望角速度曲线

为比较不同控制器的控制精度，在相同仿真环境内对文献[4]中的“PD+型姿态跟踪控制器”进行仿真，并与本文设计的控制器仿真结果对比，见图8，“PD+”表示文献[4]的仿真结果，“MRP”为本文设计的控制器的仿真结果。定义指向夹角ε为卫星本体X轴与rbt(见图1)的夹角，由ε衡量指向跟踪精度。从图8(a)可见，两种控制器均能实现指向跟踪，初始指向误差收敛并一直保持；图8(b)为ε的放大图， 40s后本文设计的控制器的跟踪精度可达到2″，可见在精度上要明显优于“PD+”控制器。

为贴近实际情况，考虑航天器质量会发生变化，对无惯量误差、1倍、6倍、10倍、20倍、30倍、40倍和50倍惯量误差δJ的情况进行仿真。由图9可见，尽管指向夹角ε随惯量误差的增大而降低，但仍可进行角秒级精度的指向跟踪控制，说明指向跟踪控制器仍然适用。

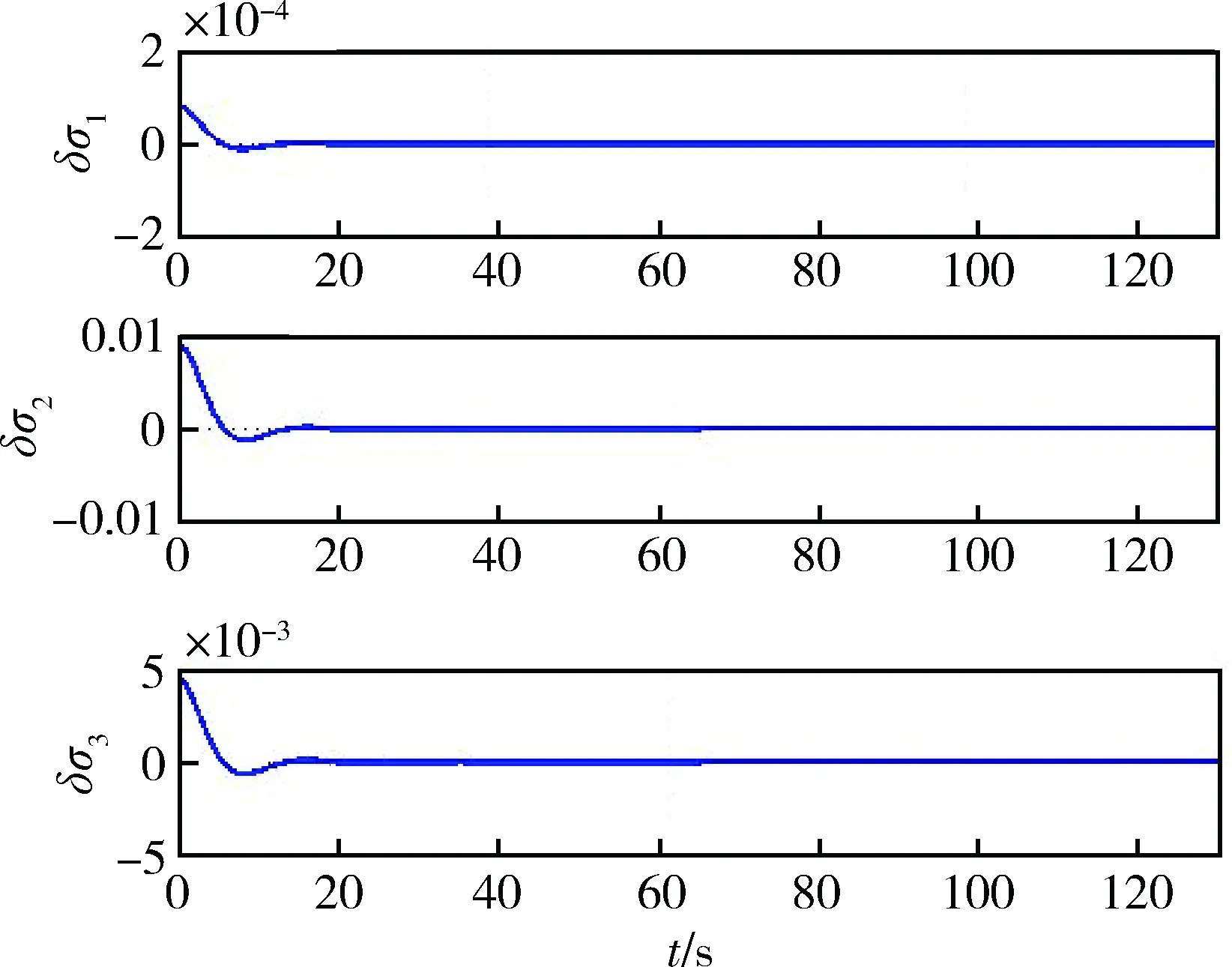
图5 相对姿态曲线

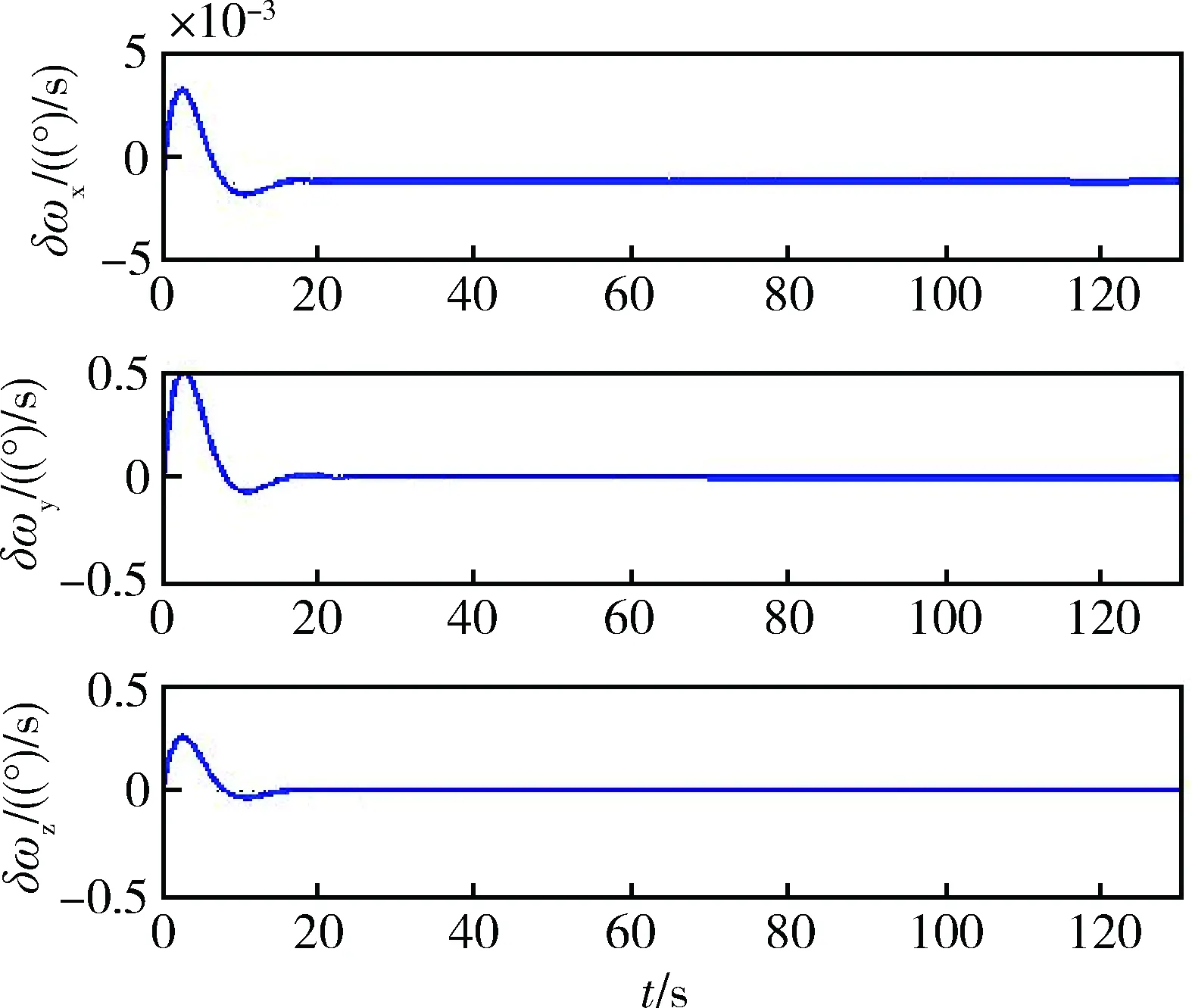
图6 相对角速度曲线

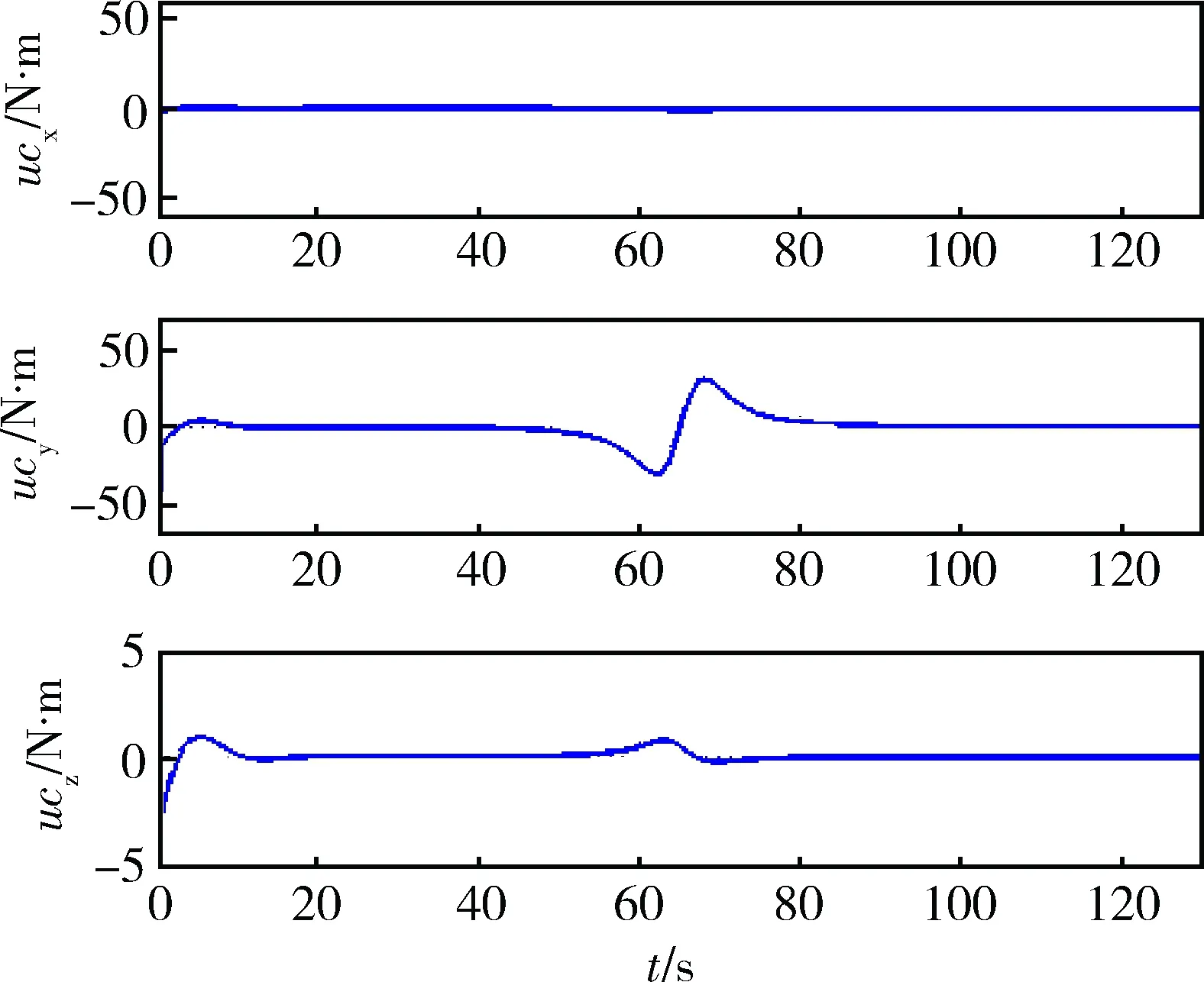
图7 控制输出曲线

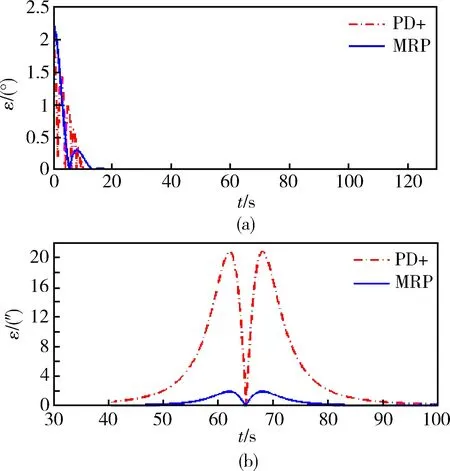
图8 不同控制律的指向夹角曲线和放大图

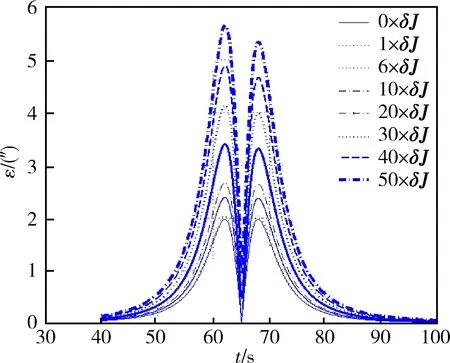
图9 不同惯量误差指向夹角放大图

5 结论

采用修正Rodrigues参数描述相对姿态，给出一种可实现角度跟踪和速度跟踪的PD型姿态指向跟踪控制器，并应用Lyapunov理论严格证明相对姿态和相对角速度渐进稳定。对控制中经常遇到的输出饱和约束问题，本文设计了增益分配律，可在提高精度的同时避免控制器输出进入饱和域。仿真结果表明，在存在初始指向偏差和饱和约束的情况下，该控制器能实现大椭圆轨道卫星对静止轨道卫星高精度姿态指向跟踪，稳态跟踪精度达到2″。当存在惯量误差时，控制器仍能实现高精度指向跟踪。

[1]WieB,WeissH,ArapostathisA.QuarternionFeedbackRegulatorforSpacecraftEigenaxisRotations[J].JournalofGuidance,Control,andDynamics, 1989, 12(3): 375-380.

[2]BilimoriaKD,WieB.Time-optimalThree-axisReorientationofaRigidSpacecraft[J].JournalofGuidance,Control,andDynamics, 1993, 16(3): 446-452.

[3]YangQ,GangC,MinX,etal.TheNonlinearControllerDesigningForSpacecraftLargeAngleAttitudeStateTracking[C]//14thAIAA/AHISpacePlanesandHypersonicSystemsandTechnologiesConference. 2006.

[4]SeoD,AkellaMR.SeparationPropertyfortheRigid-bodyAttitudeTrackingControlProblem[J].JournalofGuidance,Control,andDynamics, 2007, 30(6): 1569-1576.

[5]SanyalAK,ChaturvediNA.AlmostGlobalRobustAttitudeTrackingControlofSpacecraftinGravity[C]//AIAAGuidance,NavigationandControlConference,Honolulu,HI,pp.AIAA-2008-6979. 2008.

[6]SanyalAK,Lee-HoZ.AttitudeTrackingControlofaSmallSatelliteinLowEarthOrbit[C]//Proc.AIAAGuidance,NavigationandControlConference. 2009.

[7]ZhouZQ.SpacecraftAttitudeTrackingandManeuverUsingCombinedMagneticActuators[C]//AIAAGuidance,Navigation,andControlConference. 2010: 2-5.

[8]BhatSP,BernsteinDS.ATopologicalObstructiontoContinuousGlobalStabilizationofRotationalMotionandtheUnwindingPhenomenon[J].Systems&ControlLetters,2000,39:63-70.

[9]ThakurD,AkellaMR,MazencF.PartialLyapunovStrictification:SmoothAngularVelocityObserversforAttitudeTrackingControl[C]//AIAASpaceandAstronauticsForumandExposition,SanDiego,CA. 2014.

A High Precision Attitude Pointing Tracking Control for Spacecraft Based on the Gain Schedule

Dong Tianshu1, He Yingzi1,2

1. Beijing Institute of Control Engineering, Beijing 100190, China 2. Science and Technology on Space Intelligent Control Laboratory, Beijing 100190, China

Itisinvestigatedthatthehighprecisionandlargeangleofattitudepointingtrackingcontrolproblemforrigidspacecraftinthispaper.Forensuringtherepresentationofattitudeisgloballydefined,weusethemodifiedRodriguesparameterstorepresenttherelativeattitude.AkindofPDtypeattitudepointingtrackingcontrollerisdeveloped,whichcanguaranteetherelativeattitudeandrelativeangularvelocitybeasymptoticallystable.Furthermore,akindofgainscheduleisdesignedtoimprovetheaccuracyofcontrolandavoidthesaturationlimits.Numericalsimulationresultsthatthecontrolalgorithmisabletokeepthehigheccentricobitsatellitepointingtrackingthegeostationarysatelliteunderthesituationofexistinginitialpointingerrorandthesaturationlimits.Thecontrolalgorithmperformsrobustness,duringchangingofsatelliteinertiamatrix.

Attitudetrackingcontrol; PDtypecontrol;Gainschedule

2015-06-18

董天舒(1991-)，男，北京人，硕士研究生，主要研究方向为航天器控制技术；何英姿(1970-)，女，湖南人，博士，研究员，主要研究方向为航天器制导、导航与控制系统方案设计。

V448

A

1006-3242(2016)01-0050-07