一种可用于飞行器群系统编队及简捷重构的算法

曾志峰 陈士橹 徐敏

1.西北工业大学航天学院, 西安 710072 2.航天飞行动力学技术重点实验室, 西安 710072



一种可用于飞行器群系统编队及简捷重构的算法

曾志峰1，2陈士橹1,2徐敏1,2

1.西北工业大学航天学院, 西安 710072 2.航天飞行动力学技术重点实验室, 西安 710072

针对集中式编队法弊端及重构简捷化考虑，基于跨临界分岔变种形式提出了一种分布式群系统编队法，可使群系统在有限感知信息条件下自组织无碰撞地实现期望编队。该法通信压力低、计算资源省、鲁棒性高、扩展性好、柔性强，核心优势在于重构时仅需调节少量分岔参数便可简捷地调整切换构型。该法基于人工势场技术主要分三部分：基于跨临界分岔变种形式构造全局有序汇聚势场，基于Morse势构造成员间避碰势场及速度依赖型耗散机制。通过可行性验证及特性仿真，验证了方法的有效性和优越性。分析表明，将该法对应不同平台特征进行相应改造，可较方便地用来实施诸如小卫星群等飞行器群系统的编队任务。关键词 飞行器; 编队; 重构; 跨临界分岔; 人工势场

随着MEMS(微机电系统)技术的发展[1]，人们把更多目光投向了微小型任务平台，诸如小卫星、小型无人机等微小型飞行器。相对大型平台，微小型平台虽结构简单、功能较单一，但其可通过集群化任务应用形式来实现甚至超越大型平台的功用。

作为群系统任务的一种典型任务形式，编队由于其高任务性价比，越来越得到人们的重视并得到了广泛的研究。编队方法本质上主要分为集中式和分布式两种。集中式方法诸如跟随领航者法、虚拟结构法等在群系统成员不多、任务简单及环境不复杂的情况下尚能有效遂行编队任务，但在成员数规模较大、任务及环境复杂的情形下就显露出诸如鲁棒性低、扩展性差和柔性小等弊端。分布式方法主要以基于行为法为代表，其中行为建模多基于人工势场技术，其分布式的体系结构可以很好地克服以上集中式方法所面临的弊端[2]。Izzo基于人工势场技术开发了名为“Equilibrium Shaping Approach”的编队方法[3]，此法利用目标构型的几何对称性来消减方程数量从而求得人工行为势场各参数，可使群体成员仅在局部感知信息下自组织地编成目标空间构型。Pinciroli C等人[4]利用著名的双体势经验模型伦纳德-琼斯势[5](LJP, Lennard-Jones potential)构造局部势场，使成员在避碰同时编制成带中心正六边形局部构型，且构型中相邻成员间距与设定值几乎保持一致。诸如以上两法的分布式编队方法，均能有效地克服集中式方法存在的弊端，但同时也存在构型切换的相对不便捷问题，诸如Izzo法在切换构型时需要重新依据新构型设定目标点处驻留势场以及依据新构型的对称性来确定所有未定势场参数，Pinciroli C法在切换构型时则一般需要更换所用到的原子/分子经验势模型。

基于以上分析，本文基于跨临界分岔变种形式提出了一种分布式群系统编队方法，可使诸如微小型飞行器群等群系统有限感知信息条件下自组织无碰撞地实现期望编队，且仅需更改分岔参数便可实现不同构型间的快速切换。首先对所提方法进行简单介绍；其次通过理想任务仿真验证该法可行性；再其次通过特性仿真对方法的鲁棒性、扩展性以及柔性进行分析，最后总结该法并对其在飞行器群编队任务中的应用发展做了分析展望。

1 方法介绍

方法基于人工势场技术对群系统成员各虚拟行为进行建模，包括：基于跨临界分岔变种形式构造全局人工势场诱导成员的有序汇聚行为；基于Morse势[6]构造成员间局部人工势场遂行成员间的避碰行为。群系统各成员经前二者的协调作用，将逐步自组织、无碰撞地汇聚于预设编队点周围，并编成期望构型。在此基础上，引入速度依赖型耗散机制以确保任意初始分布条件下群系统编队均收敛。

不失一般性，采用二阶群系统模型，考虑N个同质，质量均为m，大小可忽略成员的编队任务，成员i位置、速度矢量分别为xi，vi。此时群系统中成员i的二阶运动方程可写为如下形式：

(1)

式中，US为全局有序汇聚势场，采用跨临界分岔变种形式对应势函数形式；UR为成员间避碰势场，基于Morse势构造；σ为耗散因子控制耗散快慢。

下文详细介绍各人工势场构造。

1.1 全局有序汇聚势场

动力系统中，当某个或某些系统参数以平滑方式作缓慢改变时引起系统发生性质或拓扑结构上的突变谓之“分岔”，而这些参数即为“分岔参数”。分岔可进一步分为静态、动态分岔两大类，前者讨论平衡态数目和稳定性的变化，典型如叉形分岔、跨临界分岔等；后者讨论系统在相空间中轨线拓扑结构的变化，典型如霍普夫分岔等。

利用分岔来构建全局人工势场主要利用的是分岔对应动力系统的有序演化特性以及改变分岔参数所引起的系统性质突变性。前者可用来汇聚成员并编制目标构型，后者则可用来进行目标构型间的快速切换重构。基于此思想，Derek.J.Bennet等[7]研究了利用叉式分岔、跨临界分岔及霍普夫分岔等分岔构建势场进行编队的可能。

与Derek.J.Bennet方法不同，本文基于跨临界分岔的变种形式进行全局势场设置。该变种形式一方面继承了跨临界分岔形式简单的优点，可弥补跨临界分岔在不同分岔情形下稳定平衡态均单一且对应势场最小位置非全局最小的劣势；另一方面分岔效果又与叉式分岔相似，同时对应势场函数的阶次又比叉式分岔对应阶次低，故而利用该变种形式进行编队时，一方面可获得比跨临界分岔编队法更丰富的构型；另一方面由于其势场函数阶次低，对应人工势场比叉式分岔人工势场要更平缓，将更有利于编队的控制实施及燃料节省。

本文所用跨临界分岔变种形式如下：

(2)

式中，x为动力系统状态参量，μ为分岔参数。

(3)

其平衡态稳定性可由系统雅可比矩阵特征值性质来决定，其中雅可比矩阵J为：

(4)

易知其特征值：

(5)

从而依李雅普诺夫间接法知平衡态稳定情形如下：

(6)

对应分岔图如图1所示。

图1 跨临界分岔变种形式分岔图

该变种分岔对应的势场函数为：

(7)

图2为跨临界分岔变种形式对应的势场图，当μ<0时，势场只有1个极小值点，对应于系统的稳定平衡点xe=0；而当μ>0时，势场有1个极大值点及2个极小值点，对应于系统的1个不稳定平衡点xe=0及2个稳定平衡点xe=±μ。

图2 跨临界分岔变种形式对应势场图(μ=±4)

考虑如下的二维系统：

(8)

图3(a)和(b)分别对应存在耗散机制下跨临界分岔动力系统在分岔参数μ<0，μ>0时的相图。

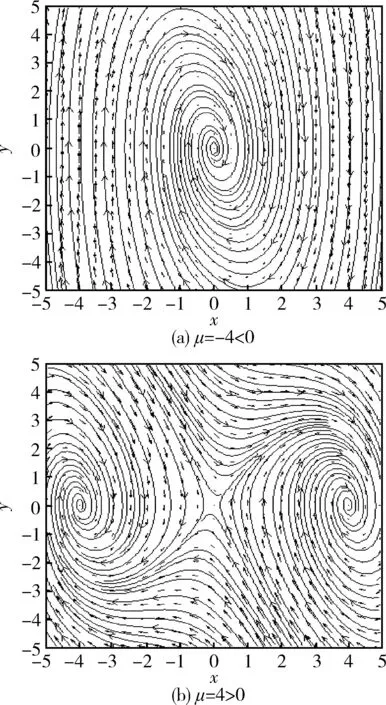
图3 跨临界分岔变种形式相图(σ=1)

图1～3从不同角度展示了跨临界变种形式对应动力系统的演化稳定及分岔特性。本法即相中这些特性，基于式(7)建立全局有序汇聚势场US，以期达到有序汇聚群系统成员编制目标构型，并在不同构型间进行简捷重构的目的。但需说明的是，式(7)仅为势场函数基本形式，实际使用时一般依据编队构型进行相应改造，具体参见下文仿真部分。

1.2 成员间避碰势场

基于Morse势建立如下成员间避碰势场：

(9)

式中，Cr为势场幅度参数；Lr为势场影响范围参数；xij=xi-xj为成员间位置矢量差。

2 仿真验证

考虑含50个同质成员的群系统，各成员大小忽略，质量均为m，零初始速度随机分布于参考坐标系o-xyz内，以原点o为圆心，rs为半径的球域内，成员i位置、速度矢量分别为xi，vi。理想条件下，假设各成员不受任何外力，可感知自身位置、速度信息及周边其它成员的位置信息，并能根据编队需要提供相应加速度。

仿真基于式(1)所示二阶群系统模型进行，其中有序汇聚势场函数基于式(7)基本形式构建：

(10)

仿真参数及结果如表1和图4所示。

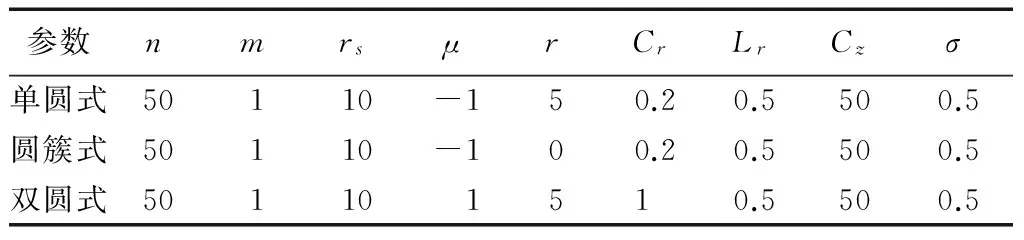
表1 仿真验证所用参数

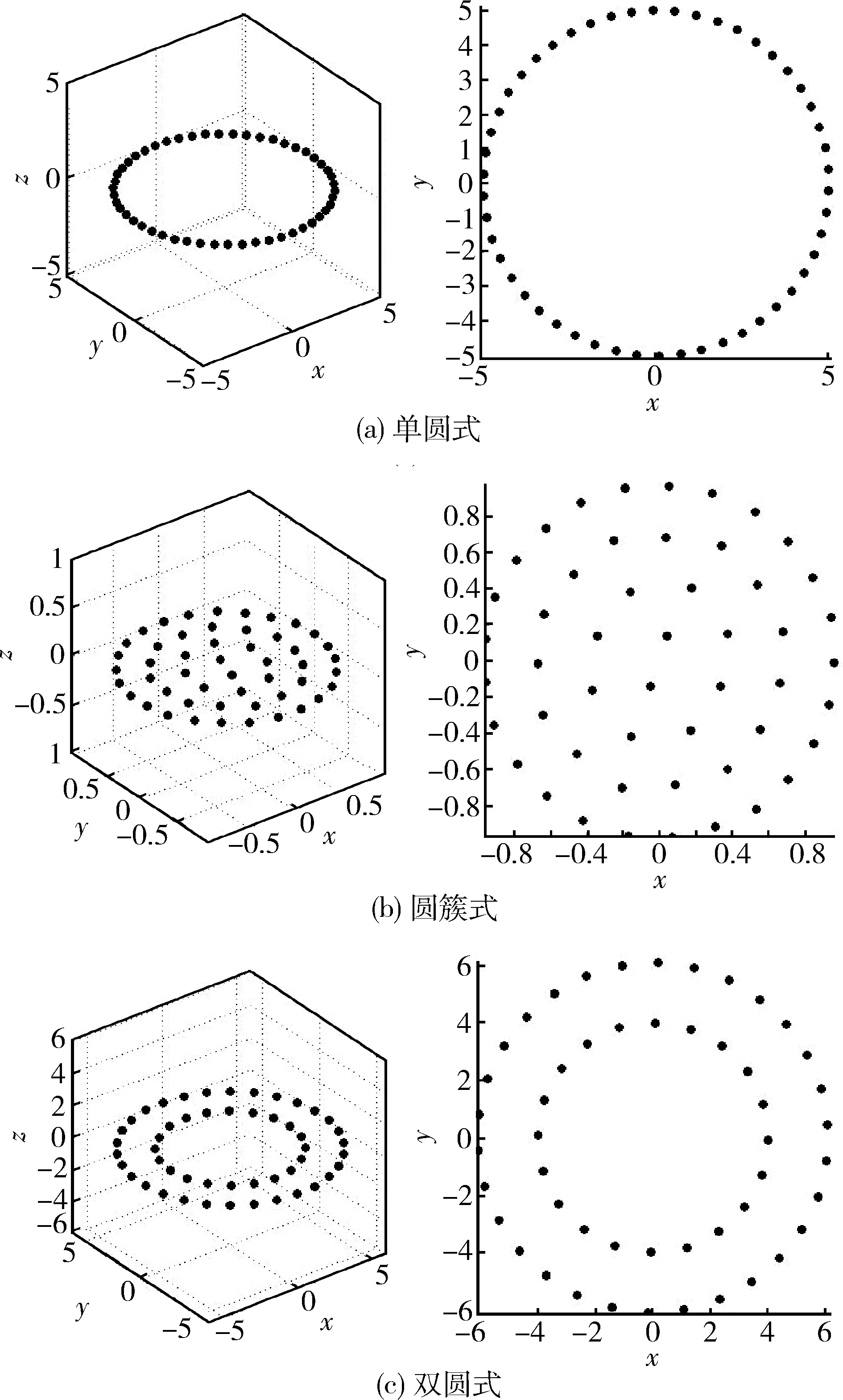
图4 仿真3D图、xy平面图

由图4可知，自由空间、理想任务条件下，基于本文方法，通过将跨临界分岔变种形式所对应势场函数的基本形式改造为式(10)所示形式，从而建立起全局有序汇聚势场，可很方便地在有限感知信息条件下使群系统自组织无碰撞地编成单圆式、圆簇式和双圆式构型，从而从仿真角度验证了本编队方法的有效性。

方法介绍部分提到了本文基于跨临界分岔变种形式进行编队的优势，即与Derek. J. Bennet文中基于跨临界分岔及叉式分岔编队相比，一方面可获得比跨临界分岔编队法更丰富的构型(跨临界分岔由于稳定平衡态单一且对应势场最小位置非全局最小，不能采用类似式(10)的处理方式编制单圆式、双圆式等构型)；另一方面可编制出叉式分岔编队法类似的构型种类，由于势场函数阶次更低，相同情形下较后者更省力省能源。以下通过相同任务条件下采用本文方法和叉式分岔编队法进行单圆、圆簇及双圆式构型的3组仿真进行对比说明以上结论。

表2 编队方法对比仿真所用参数(法一：本文编队法；法二：叉式分岔编队法)

由图5各子图可看出，相同任务条件下，无论是单圆式、圆簇式还是双圆式编队情形，本文编队法较叉式分岔编队法在系统成员动能之和∑Ei及控制力大小之和∑‖Fi‖两个指标上均具明显优势，说明同等任务条件下本文编队法较叉式分岔编队法更为省力节能。

需要说明的是，上文仿真均采用了类似式(10)的思路，对所用分岔型势场函数基本形式进行改造，实际上还可采用多种不同改造思路来得到其它构型类别，诸如图6～9所示的多种对称构型。

3 特性分析

在验证方法有效性后，以下继续考察该法在诸如失效减员、升级增员及行进间避障，并进行构型切换情形下的特性，即考察该法的鲁棒性、扩展性以及柔性(亦称“灵活性”)。简便但不失普适性，本节依然基于上节脚本进行各仿真分析。

3.1 鲁棒性

图10各子图分别对应上节完成单圆式、圆簇式及双圆式构型编队后，发生成员失效情形下(假定随机有10个成员失效，简便但不失有效性，进一步假定失效成员失效同时立即从任务空间消失)，剩余成员自动调整的各仿真过程图。由以上各图可看出，本文方法具有良好的鲁棒性，当构型发生成员失效后，剩余成员可以在其它条件不变的前提下，自动地快速进行调整，调整前后编队构型类型保持不变。

图5 编队方法对比仿真图

图6 簇式对称构型仿真对比图

图7 直线式对称构型仿真对比图

图8 单双球面、单双椭球面构型仿真对比图

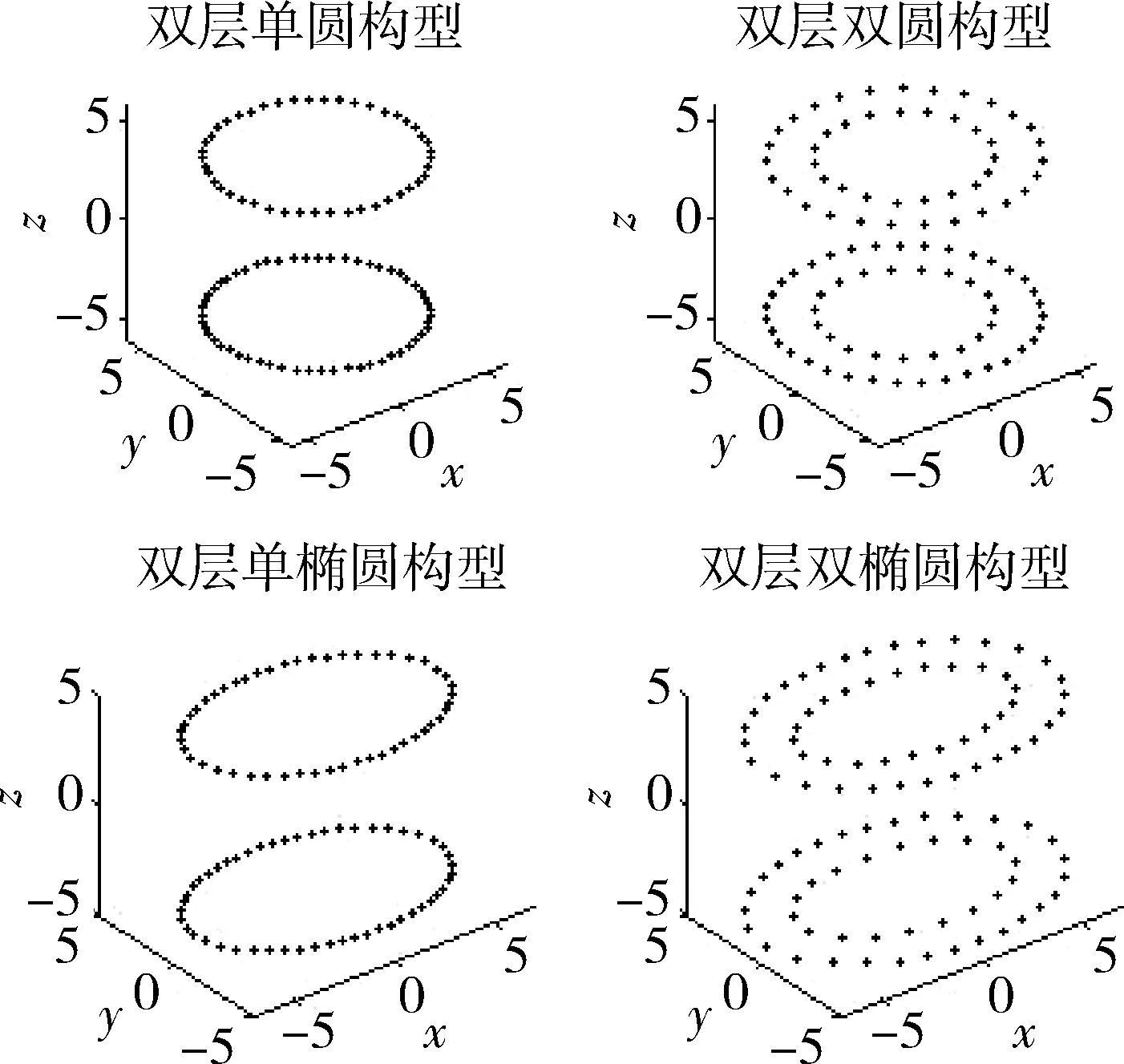
图9 层式构型仿真对比图

图10 鲁棒性仿真图

3.2 扩展性

图11各子图分别对应上节完成单圆式、圆簇式及双圆式构型编队后，增加成员情形下(假定随机增加10个成员，初始化机制与原成员相同)，新老成员一起自动扩展调整的各仿真过程图。由以上各图可以看出，本文方法具有良好的扩展性，当编队完成在构型周围随机增加成员后，新老成员可以在其它条件不变的前提下，自动地快速进行扩展性调整，调整前后编队构型类型保持不变。

3.3 柔性

通过对障碍避让及构型间灵活调整切换等脚本来考察本文方法的柔性。仿真脚本大致设置如下：

阶段1：50个成员由初始随机状态开始，匀速沿x轴正方向行进，同时编为圆簇式构型；

阶段2：成员保持圆簇式构型继续匀速前进，随后进入障碍区并在避障通过后恢复原构型；

阶段3：行进过程中，簇式构型切换为xy平面内，半径r=3的单圆构型；

阶段4：行进过程中，调整单圆构型的半径为r=5，同时改变编队平面为xz平面；

阶段5：行进最后阶段，将阶段4的单圆构型切换为双圆构型，构型处于xy平面上，内外圈半径分别为4和6。

图11 扩展性仿真图(黑点：原成员；白圈：新增成员)

具体仿真结果如图12所示，为使视角清晰不致遮蔽成员，图12(c)中采用黑圆圈表达三障碍。

由图12各子图可以看出，成员完全按照预设脚本行进，且在行进过程中顺利完成避障、构型调整、切换动作，体现了方法一定的柔性特质。方法柔性尤其体现在构型通过避障区时，由图12(a) 及(c)可看出，原圆簇式构型虽因障碍排斥发生变形但又因编队势场的作用而不至完全被破坏，并且能在通过障碍区之后迅速恢复原编队构型。

4 结束语

基于跨临界分岔变种形式提出了一种分布式群系统编队方法，可使群系统自组织无碰撞地实现期望编队。整个编队过程中，成员只需知道自身位置、速度信息以及感知周边其它成员的位置信息，即只需有限的感知信息，通信压力小；成员也无须进行复杂的积分运算而仅需简单的代数运算来进行自身的路径规划，节省计算资源。相对于传统集中式编队法，本文方法鲁棒性更高、扩展性更好、柔性更大，其最大的优势在于，仅需通过简单的分岔参数变换便能实现快速地调整性及切换性重构。此外，本文方法可编制构型丰富，可用来实施不同的任务，诸如：小卫星群系统或无人机群系统可基于团簇式或圆式构型，利用本法的简捷重构特性实施干涉测量任务；航天结构单元群系统利用簇式对称、直线式对称及层式等构型来实施空间建造任务；甚至军事平台群系统利用单双球面、单双椭球面构型实施群攻群防任务。

图12 柔性仿真图(黑点：成员；黑圆柱/黑圆圈：障碍)

显然，不同的群系统平台在利用本法实施编队任务时，需要考虑实际的通信、动力条件及其它约束，结合平台的运动特性及控制方式进行相应改造，诸如：连续小推力小卫星平台可直接基于二阶群系统模型，将本法设置的人工势场力项及速度依赖型耗散项添加到小卫星相应轨道二阶运动方程的右端，便可得到编队过程中各成员星的运动方程，进一步设定各成员感知半径、动力幅值后便可顺利实施编队，篇幅所限，具体改造过程另文阐述。

[1]OsianderR,DarrinMG,ChampionJL.MEMSandMicrostructuresinAerospaceApplication[M].Florida:CRCPress, 2006.

[2] 王祥科，李迅，郑志强.多智能体系统编队控制相关问题研究综述[J].控制与决策，2013，28(11)：1601-1613. (WangXiangke,LiXun,ZhengZhiqiang.SurveyofDevelopmentsonMulti-agentFormationControlRelatedProblems[J].ControlandDecision, 2013，28(11)：1601-1613.)

[3]IzzoD,PettazziL.AutonomousandDistributedMotionPlanningforSatelliteSwarm[J].JournalofGuidance,ControlandDynamics, 2007, 30(2): 449-459.

[4]PinciroliC,BirattariM,TuciE,etal.Self-OrganizingandScalableShapeFormationforaSwarmofPicoSatellites[R].IRIDIA-TechnicalReportSeries,TechnicalReport,No.TR/IRIDIA/2008-009,Bruxelles:IRIDIA, 2008.

[5]BurkertU,AllingerNL.MolecularMechanics[M].Washington.D.C:AmericanChemicalSociety, 1982:177.

[6]D’OrsognaMR,ChuangYL,BertozziAL,etal.Self-propelledParticleswithSoft-coreInteractions:Patterns,StabilityandCollapse[J].PhysicalReviewLetters, 2006, 96(10):104302.

[7]BennetDJ,McInnesC,SuzukiM,etal.AutonomousThree-dimensionalFormationFlightforaSwarmofUnmannedAerialVehicles[J].JournalofGuidance,ControlandDynamics, 2011, 34(6): 1899-1908.

[8]BennetDJ,McInnesC.PatternTransitioninSpacecraftFormationFlyingUsingBifurcatingPotentialField[J].AerospaceScienceandTechnology, 2012, 23(1): 250-262.

The Novel Algorithm for Formation and Simple Reconfiguration of Swarming Flight Vehicles System

Zeng Zhifeng1,2, Chen Shilu1,2, Xu Min1,2

1. School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China 2. Science and Technology on Aerospace Flight Dynamics Laboratory, Xi’an 710072, China

Regardingshortcomingsofthecentralizedformationmethodsandtheneedsofsimplifiedreconfiguration,adistributedformationmethodofswarmsystemisproposed,whichisbasedonavariantoftranscriticalbifurcation.Byusingthismethodandmakinguseoflimitedsensorialinformation,aswarmsystemcanachievethedesiredformationconfigurationsinaself-organizedmannerwhilethecollisiondoesnotoccur.Thismethodhasthecharacteristicsoflowcommunicationpressure,computationresourcessaving,highrobustness,goodscalabilityandmoreflexibility,anditscoreadvantageisthatitcanadjustandswitchconfigurationssimplybychangingonlyafewbifurcationparametersinreconfiguration.Theartificialpotentialfieldtechniqueisutilizedinthismethod,whichcanbedividedintothreeparts:aglobalorderedconvergenceartificialpotentialfieldbasedonavariantoftranscriticalbifurcation,alocalcollisionavoidancepotentialfieldamongagentsbasedontheMorsepotentialfunctionandthespeed-dependentdissipationmechanism.Thefeasibilityandsuperiorityofthenewmethodologyisverifiedbythesimulationresultsunderidealconditions.Theanalysisofthepapershowsthatthisnewmethodcanbeeasilyusedtoperformactualformationmissionsbymakingsomesimplemodificationsforrealswarmsystems,suchasmicrosatellitesswarm,etc.

Flightvehicle;Formation;Reconfiguration;Transcriticalbifurcation;Artificialpotentialfield

2015-09-14

曾志峰(1983-)，男，江西丰城人，博士研究生，主要研究方向为飞行器动力学与控制、群体控制；陈士橹(1920-)，男，浙江东阳人，原苏联莫斯科航空学院副博士，教授，主要研究方向为飞行器动力学与控制；徐 敏(1956-)，女，西安人，博士，教授，主要研究方向为飞行器动力学与控制。

V529.1

A

1006-3242(2016)01-0029-08