《非零应矩弹性理论》下压杆稳定临界力及实验验证
2016-08-10黄双华韩文坝
刘 帅 郭 剑 黄双华 韩文坝
(攀枝花学院土木与建筑工程学院 四川攀枝花 617000)
《非零应矩弹性理论》下压杆稳定临界力及实验验证
刘 帅 郭 剑 黄双华 韩文坝
(攀枝花学院土木与建筑工程学院 四川攀枝花 617000)
《非零应矩弹性理论》推导出来的压杆稳定临界力公式,与现行弹性理论欧拉压杆稳定临界力公式完全不同。为了验证其正确性和准确性:我们大学生创新创业科研组,对压杆稳定临界力进行了实验测定;用实验值与两种理论值相对比,来判定哪种理论与实验值相符合,就是正确的理论。
压杆稳定;弯矩;柔度;临界力;欧拉公式
引言
大型工程由于压杆失稳,造成坍塌事故,层出不穷。给人类生命财产造成严重损失。追究其原因:除质量事故外,主要是由于弹性理论中的问题造成的。下面对弹性理论存在的问题加以简介(详见非零应矩弹性理论[1])。
1 现行弹性理论存在的无法解决的问题
(1)受相等、相反力偶作用的等直杆部分体不能处于平衡
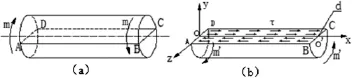
图1 圆柱扭转部分体不能处于平衡
如图1(a)受相等、相反力偶作用的等直杆,假想地沿中心轴线,剖开成两个半圆柱体,则每个半圆柱体都不能平衡;注意:两端外表面只有力偶矩作用,没有应力。圆柱面(ABO′O)和(CDOO′)上,由剪应力互等定理的导出的剪应力τ[2]构成的剪力,方向相反、相等,处于平衡(省略计算)。而其剪力对Y轴的力矩都为顺时针方向,不能保持其平衡,这与实际不符。
(2)受纯弯曲的矩形梁部分体不能平衡
如图2(a),两端受相等、相反力偶作用的矩形梁,其弯矩图如图2(c)所示。其剪力图为零[3]。假想地把梁沿中性面剖开,成上下两部分,再用垂直于X轴的平面(nn),把梁切成左右两个部分,即梁被切成四个部分。以左段上、下两部分为例,见图2(d)和(e),此二段梁只受拉应力或压应力的作用,都不能处于平衡(注意梁端面没有应力作用)。这与实际完全不符。扭转和弯曲不平衡实例很多,不多列举。详见《非零应矩弹性理论》中的实例。
要保持图1(b)半圆柱体扭转的平衡,只有等直杆内没有真剪应力(其剪应力只是相当应力);纯弯曲没有正应力(其正应力只是相当应力)。这就是弹性理论必须用应矩理论加以修正的原因之一。
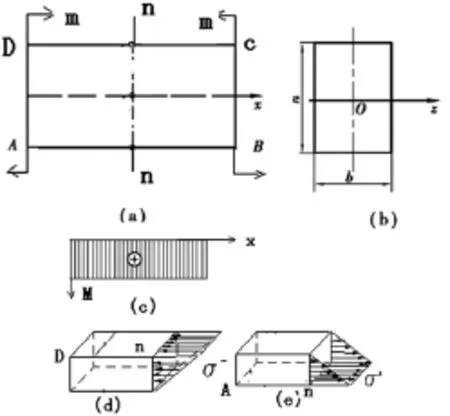
图2 纯弯曲梁部分体不能处于平衡
(3)圆轴扭转剪应力破坏了平面假设[4](详见《非零应矩弹性理论》P11)。
(4)圆轴扭转剪应力互等定理互相矛盾(详见《非零应矩弹性理论》P14~16)。
(5)圆轴扭转剪应力和牛顿第三定律产生矛盾(详见《非零应矩弹性理论》P14~15)。
(6)第三、第四强度理论[5]会得出,无论多么大的应力都不会使受三向等应力拉伸的物体破坏,哪怕此物体是用萝卜做成的正方体也不会破坏,这完全不符合实际。
2 现行弹性理论认定:作用在单位面积上力矩的极限(应矩)恒为零[2]的结论,必须加以修正。
理论力学[6]指出:受外力作用的物体向任意点简化都得到主矢和主矩。当应矩恒为零时,则其主矩也恒为零。这就违背了上述理论力学的基本原理。《非零应矩弹性理论》证明了内力的应矩恒等于零;外力的应矩不等于零。《非零应矩弹性理论》也证明了:弯曲没有正应力,而压杆稳定临界力欧拉公式[7]是用正应力理论推导出来的。因此,必须用弯应矩理论加以修正。
3 应矩理论下的压杆稳定临界力公式
应力理论下压杆稳定临界力欧拉公式为:

式中:E——材料的弹性模量,钢材E=2.1×1011,N/m2。
IZ——对中性轴的惯性矩。对于圆形梁
μ——杆件两端约束的长度系数。
l——杆长。
用类比的方法可以得出,应矩理论下的压杆稳定临界力公式[1]:

式中:Gw——为弯曲弹性模量[1],实测45号钢:Gw=2.1×109,N/m;
SZ——绝对静矩:圆形杆
4 两种理论的压杆稳定临界力之比
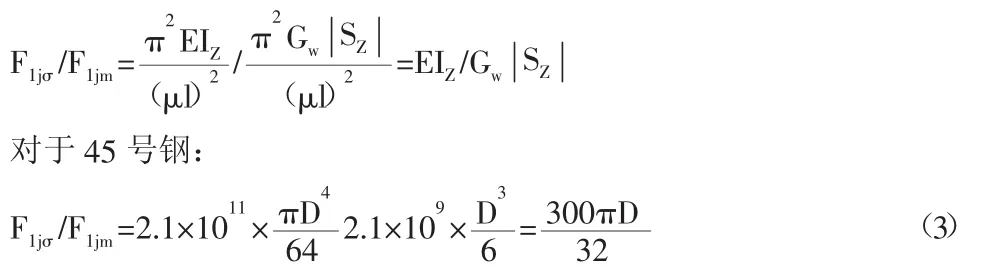
式(3)说明两种理论下,压杆稳定临界力之比与直径D的大小有关。
5 两种理论下,压杆稳定临界力相等时临界直径
由(3)式,F1jσ=F1jm时:

直径D*为两种理论压杆稳定的临界直径。它的物理意义:当直径D*<34mm时,F1jσ<F1jm,说明F1jσ是能保证压杆稳定安全;当D*>34mm时,F1jσ>F1jm,说明应矩理论计算出的F1jσ是不能保证压杆稳定安全。
由于条件限制,D*>34mm不能进行实验。只做D*<34mm的实验。
只要判定两种理论值,哪个与实验值相接近,哪个就是正确的理论。
6 压杆稳定临界力的实验测定
(1)原理:实测(压杆长为l,直径为D的45号钢和碳素结构钢杆)圆压杆稳定的临界力与两种理论的临界力的计算值相对比,与实验值接近者证明其理论的正确性。
(2)时间:2015年10月。
(3)实验地点:攀枝花学院测试分析中心。
(4)实验材料:45号钢和碳素结构钢圆杆。
(5)实验材料尺寸:一组四根,D=14.41mm,长l=400mm。二组两根,D=18.58mm,长l=400mm。
(6)实验设备:INSTRON-英斯特朗——(美国产拉压试验机)最大荷载100kN,最大行程1.5m。
(7)压杆两端连接方式:拉压实验机底座平台上,设有一直径d=20mm圆孔,把压杆下一端插入圆孔中;杆件上端与拉压实验机加力板直接接触。则压杆连接的长度系数介于1~2之间,本实验取μ=1.4(见张耀春主编,周绪论红副主编钢结构设计原理P190:钢压杆连接*的取值范围)。
(8)保证压杆稳定实验值准确性的措施[8~10]。
①保证实测实验杆的直径和长度的准确性。
②保证实验杆表面光洁度、垂直度、两端面平整。
③保证杆件内无夹杂、砂眼、裂纹(由于条件限制,没有做此项工作;虽然对实验有影响,但是对于两种理论造成的影响是相同的)。
④压杆稳定实验加载时,要保证杆件端面与机座底面垂直。
⑤本实验加载与变形全程电脑自动记录(有记录可查)。
7 应力、应矩压杆稳定临界力理论值与实验值对(见表1)
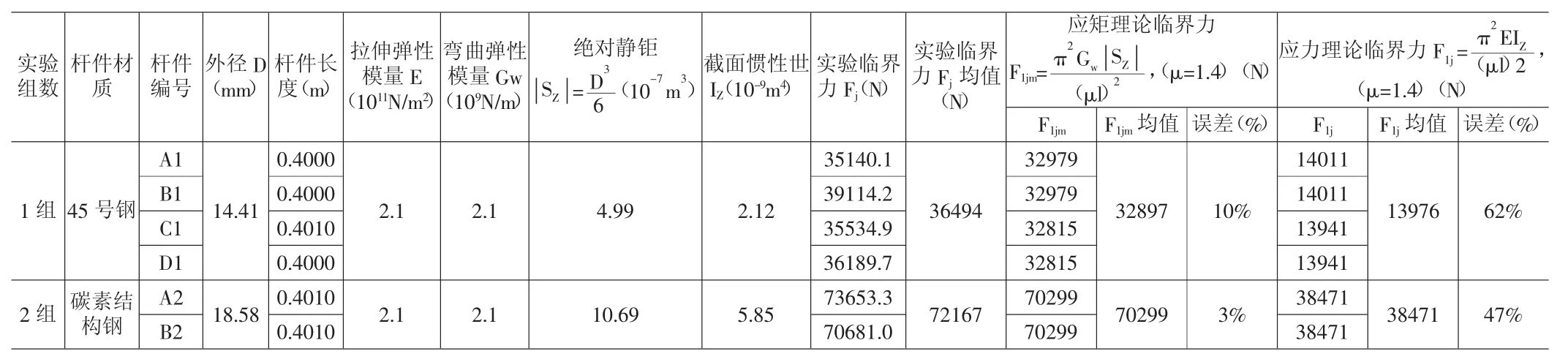
表1 应力、应矩压杆稳定临界力理论值与实验值对比表
8 结论
对比表1可见:两组实验数据都与应矩理论计算值相接近:一组误差为10%。二组误差为3%;而应力理论的计算值误差很大:第一组误差为62%,第二组误差为47%。可见应矩理论是正确的。这就找到了直径D*>34mm时的压杆失稳事故经常发生的根本原因:是应力理论的错误造成的。
[1]韩文坝,黄双华.非零矩阵弹性理论[M].重庆:重庆大学出版社,2013:1~21.
[2]钱伟长,叶开沅.弹性力学[M].北京:科学出版社,1956:45~51,45.
[3]刘鸿文.材料力学[M].北京:高等教育出版社,2000:126~127.
[4]张如三,王天明,等.材料力学[M].北京:中国建筑工业出版社,2008,48.
[5]赵九江,张少实,王春香.材料力学[M].哈尔滨:哈尔滨工业大学出版社,2002:197~199.
[6]哈尔滨工业大学理论力学教研室.理论力学Ⅰ[M].北京:高等教育出版社2009,88.
[7]单祖辉.材料力学[M].北京:高等教育出版社,2005:307~308.
[8]赵五一.压杆失稳[J].北京:建筑工人,2001(9):36~37.
[9]汤红.结构设计中的一些常见问题探讨[J].江西煤矿科技,2005,2:35.
[10]随炳强,邓长根.钢压杆稳定加固研究进展[J].江北工程大大学(自然科学版)2009(26),1:21~28.
TU311.2
A
1004-7344(2016)29-0283-02
国家级大学生创新创业科研项目(2014CXCY021)。科研组成员:寇云蛟,杨运超,王梁鑫,张川江。
2016-9-20
刘帅(1995-),男,四川简阳人,攀枝花学院2013级房建二班在读本科生。郭剑(1978-),女,四川人,副教授,硕士,从事力学教学和研究工作。黄双华(1957-),男,四川人,教授,硕士,从事结构工程、岩土工程研究工作。
韩文坝(1938-),男,辽宁人,教授,本科,从事力学基础理论研究工作。
