系统整体和子区域产出策略均衡研究
2016-08-10曾小平
曾小平
(开封大学 科研处,河南 开封 475004)
系统整体和子区域产出策略均衡研究
曾小平
(开封大学 科研处,河南 开封 475004)
摘要:以传统经济增长理论为出发点,以新经济增长理论为目标,研究系统整体和子区域之间的均衡发展关系。其主要目的是研究区域经济在发展过程中如何优化区域发展策略,以达到产出均衡。研究要点有三个:第一,子区域的发展均衡策略;第二,系统整体的发展均衡战略;第三,考虑福利问题的系统发展战略。
关键词:系统整体;子区域;均衡发展;区域经济
以增长为中心的发展战略是以实现经济发展为目标的[1]。该发展战略仅重视发展的手段,忽视了发展的目的,不重视普通民众的需要。随着经济社会的进步和人们认识水平的不断提高,20世纪80年代产生了新增长理论。新增长理论把人的发展置于首要位置,认为经济增长是物质资本积累和劳动力的增加这两个因素同技术进步这一外在因素结合的结果,人的能力在发展过程中起着关键作用。传统的增长理论关注的是资本、劳动力和技术,而新增长理论关注的是人力资本,是以人为中心的发展思想的体现[2]。
新增长理论认为,区域间存在着资源禀赋、资本、劳动力和技术等各方面的差异,这些差异使得区域间的非均衡发展成为常态。如果仅依靠市场机制来对区域间的差异进行调节,将导致社会问题的积累和突变。因此,区域管理者应主动对区域间的差异进行调控,以求得区域间经济和民生的均衡发展[3]。笔者从区域产出角度和非市场行为的额外投入策略入手,运用均衡分析方法,对系统整体和子区域的均衡发展模式进行研究,并得出其优化模型。
一、模型的建立
在不考虑福利和公平的情况下,系统和子区域的发展目标是产出的最大化。笔者正是以产出为出发点来研究子区域和系统整体之间的均衡关系的。在研究中为了简化分析,假定系统产出仅受两个变量约束:一是产出函数,即资本、劳动力和技术的函数;二是系统的调控,即政府或管理者对资源的非市场机制调控[4]。
在市场机制约束下区域的发展与产出要素相关。区域的资本愈多、劳动力愈丰富、技术愈发达,其产出就愈多。
如果区域管理者从社会福利最优化(或区域均衡发展)的角度出发,对区域生产以均衡发展为目的进行调控(这种调控明显是市场机制之外的),就必然导致对发展中区域进行额外的(相对于发达区域)投入。这种投入倾斜可以帮助发展区域获得超过单纯市场机制下其所能达到的区域产出[5]。笔者把这种投入倾斜称为额外产出投入(额外的投入会导致额外的产出,以实现均衡),额外产出投入效应可以帮助区域管理者通过子区域调控来实现区域均衡发展。
在市场机制和非市场机制中,区域间如何达到均衡,系统如何得到优化及至系统的总体福利如何实现,就是笔者研究的内容。
在研究中先建立模型,而后在建立的模型中作了如下的定义和假定。
第一,笔者把研究的系统分为若干子系统,即子区域i,子区域总个数为M。
第二,从t=0年开始研究,不考虑区域产业结构、资源禀赋及技术等方面的差异,各区域的生产函数相同,均用P表示,P=P(K,L,T,xi)。
第三,在区域经济处于发展阶段时,生产具有规模经济效应,P′(X)> 0;在区域经济处于发达阶段时,生产不具有规模经济效应,P′(X)<0。为了使分析简便化,假定区域经济处于加速阶段,即P′(X)<0。
第四,不考虑系统外因素对区域和区域各子系统的影响,生产函数P和系统外因素不相关。
第五,不考虑系统内因素的约束及变动对生产函数的影响,如市场、结构等。
第七,区域管理者的目标为产出最大,而不受其他因素,如市场、社会满意度等约束。
对于子区域i来说,管理者为提高其产出,将不断提高额外产出投入,以达到产出的最大化。若定义子区域i的产出为πi,则有
πi=(P+ei)xi,
(1)
其中i=1,2,…,M。
二、子区域产出收益的完全信息静态Nash均衡
额外产出投入存在着机会成本,它对子区域的产出存在负效应。为了方便分析,定义λ为产出机会成本,额外产出投入的机会成本为λ′。若子区域基于额外产出投入ei的产出收益为Wi,则
Wi=πi-λ′=Pxi-(λ+1)eixi,
(2)
其中i=1,2,…,M。

(3)其中i=1,2,…,M。

(4)
(5)
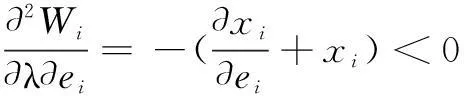
(6)
由式(4)、式(5)、式(6)可得以下结论:
第一,子区域的额外产出投入是λ的减函数。随着产出机会成本的增加,子区域的额外产出投入将减小;随着产出机会成本的降低,子区域的额外产出投入将增加。
第二,当机会成本λ<λE时,其额外产出投入为正,此时子区域的最优策略是尽可能增加额外非市场行为的投入。
第三,当机会成本λ>λE时,其额外产出投入为负,此时子区域的最优策略是不增加任何额外非市场行为的投入。
第四,当机会成本λ=λE时,其额外产出投入为零,此时子区域通过额外产出投入并不能改变子区域的产出,将没有动力采取额外投入行动。
三、区域均衡
区域管理者在(1)式条件下,将不断地调整其区域经济发展战略和策略,促使本区域的产出最大化,此时就会有
(7)
其中i=1,2,…,M。
对方程组(7)求微分可得
(8)
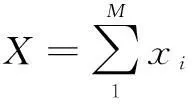
(9)
其中Δ=(M+1)P′+XP″<0,i=1,2,…,M。
对方程组(9)进行分析,我们可以得出以下结论:
第一,从第1个方程可看出,系统整体的产出是额外产出投入的减函数。在系统加大对子区域的政策投入和调控力度时,子区域的产出产生正效应,但对于系统整体来说,产出是负相关的。对于系统来说,减少对子区域的干预和调控,将更有利于系统产出的增加。
第二,从第2个方程可看出,系统的产出函数是额外产出投入的增函数。系统在加大对子区域的额外产出投入时,产出函数上升;系统在减少对子区域的额外产出投入时,产出函数下降。
第三,从以上的分析可以看出,系统对子区域实施额外产出投入,其结果是在区域之间进行要素的调控和转移。从整体的角度来看,非市场机制的要素调控对总体产出产生负效应。
第四,从第3个方程可以看出,额外产出投入是子区域产出的减函数。随着生产的不断发展,系统应减少对区域的管理和约束。
四、社会总福利的Nash均衡
通过综合子区域产出收益可以得到系统的产出收益。由式(9)可知,对于系统来说,减少对子区域的干预和调控,将有利于系统产出的增加。这也正是市场经济对于政府角色的定位——减少干预,让市场发挥其资源配置的作用。
然而,市场的作用并不能代表全部。市场只能解决效率问题,而对于社会福利却显得无能为力。如何在效率优先的前提下使社会福利尽可能地实现最大化,就成为政府面临的问题。这也正是政府调控存在的最重要的理由。由于笔者是从产出的角度进行分析的,为了使分析具有系统性和统一性,对于社会福利的理解也将从产出的角度来进行定义和解释。
系统总区域产出的总收益为
MW=PX-(λ+1)eX。
(10)
对式(10)求导得

(11)
考虑到社会民众的福利V,从消费者福利的角度可以看到产出对于社会民众福利的影响,即
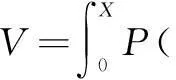
(12)
对式(12)求导得
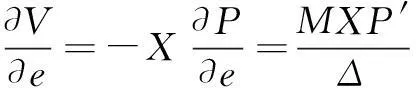
(13)
社会总福利Ω为以上两者之和,即
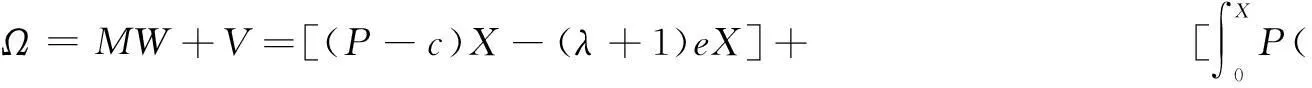
(14)
对式(14)求导得
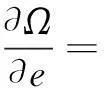
(15)
由于子区域追求其产出收益最大化,则将式(3)代入式(15)得

(16)
令式(16)为0,得到社会产出总福利的均衡式
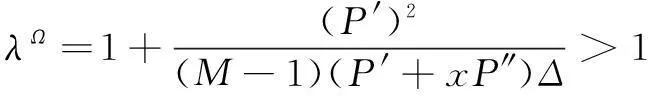
(17)
当式(17)成立时,Nash处于均衡状态。从式(16)和式(17)可知:
第一,当机会成本λ>λΩ时,∂ΩN/∂e<0,总产出福利是λ的减函数。因为存在更加有利的其他投资机会,所以此时政府对于区域间的要素调控将不利于系统总体福利的增加。
第二,当机会成本λ<λΩ时,∂ΩN/∂e>0,总产出福利是λ的增函数。因为不存在更加有利的其他投资机会,所以此时政府对于区域间的要素调控将有利于系统总体福利的增加。
第三,当机会成本λ=λΩ时,∂ΩN/∂e=0,总产出福利与λ不相关,此时政府对于区域间的要素调控与社会的总产出福利不相关。
五、结语
一般认为,市场机制是调节经济的最好方式。由上述研究得出的结论可以看出,在区域发展问题上管理者采用调节手段是必不可少的。虽然政府对较为落后的区域进行要素调控转移是必要的,但是也应该考虑市场要素的价值。这也说明政府在对较为落后的区域进行要素调控转移时不能抛开市场机制。
笔者对系统整体和子区域产出的研究还存在一些局限性:一是对出产出函数没有考虑市场需求,二是对均衡的分析没有从多周期的角度展开,三是没有进行量化研究与实证分析。
参考文献:
[1]陈秀山,张可云.区域经济理论[M].北京:商务印书馆,2005:165-167.
[2]胡兆量.中国七个经济区域评价[J].经济地理,1997(1):1-5.
[3]吴殿庭.区域经济学[M].北京:科学出版社,2003:48-49.
[4]李晓冰.中国区域经济协调发展理论与实践初探[J].现代商业,2010(8):58-60.
[5]秦耀辰.区域系统模型原理与应用[M].北京:科学出版社,2004:26-28.
[6]张维迎.博弈论与信息经济学[M].上海:上海人民出版社,2001:152-158.
【责任编辑李敬】
收稿日期:2016-03-07
基金项目:河南省教育厅重点科研项目(15B413003)
作者简介:曾小平(1974—),男,湖北武汉人,副教授,博士,研究方向:区域经济学。
中图分类号:F270
文献标识码:A
文章编号:2095-7726(2016)07-0015-03
