浅谈数列的极限

黄玉兰

（湖南工业职业技术学院数理教研室）

浅谈数列的极限

黄玉兰

（湖南工业职业技术学院数理教研室）

结合古代的极限思想，介绍了数列极限的概念和求数列极限的基本方法——观察法，通过举例并总结了常见数列的极限。

概念；极限思想；观察法

极限是高等数学中一个非常重要的知识点，而作为极限中最基础的内容——数列的极限，是学习极限的入门知识。接下来介绍极限的概念以及求数列极限的基本方法——观察法。

一、古代的极限思想

极限思想在我国已有很深的渊源，早在公元263年，刘徽（注解了《九章算术》）就提出了“割圆术”，大概思路如下图所示：

在面积为S的圆内作内接三角形，三角形的面积记为S1，再作内接正六边形，面积记为S2，再作内接正十二边形，面积记为S3，如此下去，得到一个数列，从几何直观上不难看出，当n无限增大时，Sn无限地接近圆的面积S。

《庄子·天下篇》中提到：一尺之槌，日取其半，万世不竭。第一天取，第二天取，第三天取1，如此下去，这是一个公比为的等比数列。随着n的逐渐增大，所取的长度越小，越来越趋近于0。

由以上两个例子我们可以看到，当n越大，数列的项越来越向一个确定的常数靠近，这个常数就是我们数学上讲的数列的极限。

二、数列极限的概念

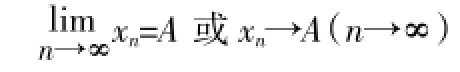
根据定义注意以下三点：

（1）若极限存在，极限必唯一。

（2）xn→A表示xn趋近于A，并不一定能取到A。

（3）常数列的极限为该常数本身。

根据极限的定义可知，求数列的极限主要看当n增大时，数列项的趋势。

三、用观察法求数列极限

观察法：通过观察数列项的趋势，以此来判断数列是否存在极限以及极限是多少。下面通过举例来介绍这个方法结算方式：

例3.判断数列an=（-1）n的极限是否存在？

解：列出前面几项为：-1，1，-1…，-1与1交替出现，没有趋近某个确定的常数，所以极限不存在。

例4.判断数列an=（-2）n的极限是否存在？

解：列出前面几项为：-2，4，-8…，正负值交替出现，值越来越趋近无穷大，不趋近某个确定的常数，所以极限不存在。

以上均为等比数列求极限情况，下面可以对等比数列的极限情况总结一下：

下面来看几个幂数列的极限情况：

例5.判断数列an=n3的极限是否存在？

解：列出前面几项为：1，-8，27，…，正负值交替出现，值越来越趋近无穷大，不趋近某个确定的常数，所以极限不存在。

对于幂数列的极限情况可总结如下：

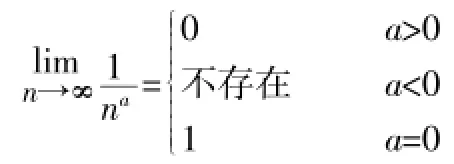
最后我们来看一个比较特殊的数列：

四、小结

数列极限是极限知识的基础知识，以上对等比数列、幂数列极限公式的总结也可以推广到求函数的极限。观察法是求数列极限最直观的方法，当然任何方法都不是万能的，在计算中要学会方法与方法的结合。

周志燕，程黄金.高等数学［M］.东北大学出版社，2014：11-15.

·编辑温雪莲

0171

A

黄玉兰，出生于1983年，湖南娄底人，硕士研究生，讲师，研究方向：数学教育，数学规划及其物流中的应用。