尝试 联想 发现——从一道题的多解谈起

王国荣

（浙江省义乌第二中学）

尝试联想发现
——从一道题的多解谈起

王国荣

（浙江省义乌第二中学）

苏霍姆林斯基说：“在人的心灵深处都有一种根深蒂固的需要，这就是希望自己是一个发现者、研究者、探索者。”德国教育家第斯多惠说：“一个好的教师应该教人去发现真理。”数学教学的核心就是要教会学生怎样分析问题，怎样探索解题思路。无论是新授课还是习题课，教师讲题始终要坚持分析地讲，要充分暴露解题途径的寻找过程，“为什么要这样做”比“这样做”更重要，并注重优化，注意反思，突出题目的本质，优化解题过程与方法，逐步培养学生思维的灵活性、深刻性和创造性，提升学生的思维品质。下面笔者从一道题出发，对它进行多角度的思考和挖掘，以求拓宽学生思维的广度和深度。

一、常规解法

分析1想到求函数最值，最容易想到的是利用单调性。但这个函数中，第一部分是减的，第二部分是增的，整个函数究竟是减还是增？

本题利用单调性求最值，首先要求出导数，再求出单调区间，最后利用单调性求出最值。思路清晰，但是运算量较大，费时且较易出错。

分析2注意到4-x+x+5=9，而且右边是非负的，因此可以通过两边平方把右边的两个根号减少为一个，转化为熟悉的二次函数最值问题再解决。

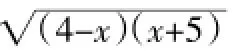
一题多解要“见机行事”，一般通性通法要讲，而且要着力落实。但多数高考题都有一个显著特征：求解入手较宽。因此方法往往就呈多样性，不同方法的选择将会产生不同的解题效果。而我们都希望学生能在最短的时间内用相对较好的方法解决问题，这就需要在平时养成优化解法的习惯，着力于培养优秀的数学思维。

而数学是充满联想的，因此，数学解题教学应该引导学生对题目隐含条件或者结构特征进行分析，为学生解决问题提供“机会和可能”，教师适时给予学生必要的数学学习方法指导，培养学生思维的灵活性。

二、联想迁移

联想迁移是通过对同一表达式或问题的不同解释，将参数视为常数、变数、未知数等多种角度，这样就可以获得各种解题方法。而每种方法都有它的思维切入点，一题多解，不仅丰富了解题思路，同时也使一些基本知识点、基本应用方法等得到了充分地展示，对于培养学生思维的灵活性会起到积极的影响作用。

在本题中注意到（4-x）+（x+5）=9，联想a2+b2=9，可以利用不等式求最值、利用三角函数进行等价转换、利用圆的方程转化为解析几何问题，再分别利用均值不等式、三角换元、数形结合等来解决它。

解法3利用基本不等式解题

解法4通过换元，把问题转化为三角函数问题解决。

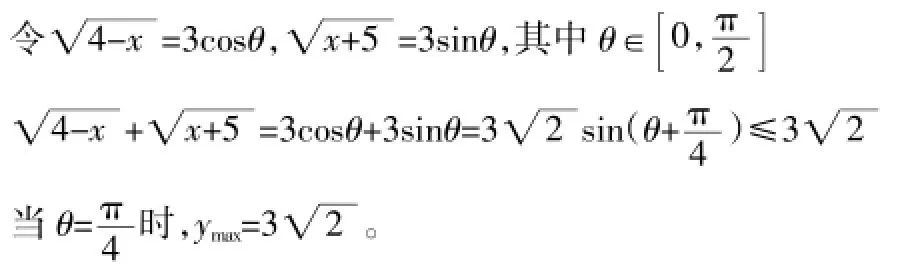
解法5利用圆的方程进行转化

已知a2+b2=9，a≥0，b≥0求y=a+b的最大值。

从而可以得到多种解题思路。

思路2：利用直线与圆位置关系d≤r，可以求得ymax=3。

思路3：可以考虑利用数形结合解决。

如图所示，可以求得ymax=3

三、思维拓展

解题教学中，有的问题有多种解题方法，有些解题方法新颖，解题思路独特，多角度地分析和挖掘问题的解决方法，有利于开阔学生的思路，引导学生灵活地掌握知识的纵横联系，培养思维的灵活性。在本题中，我们还可以进一步进行思维拓展，构造出相应的式子解题。

解法6构造向量解题

可以看出当前电力系统在我国人民的日常生活中有十分重要的作用，因此很有必要增强电力系统运行的自动化和智能化程度，以更好满足当前人民的使用需求。可以通过试用各项电气工程自动化技艺和电力设施，进一步增强电力系统的运行质量和运行效果，并且也为后期的维修和检修工作提供了便利。与此同时，也极大地节省资金和人力资源的投入，对系统的发展有积极的促进作用。

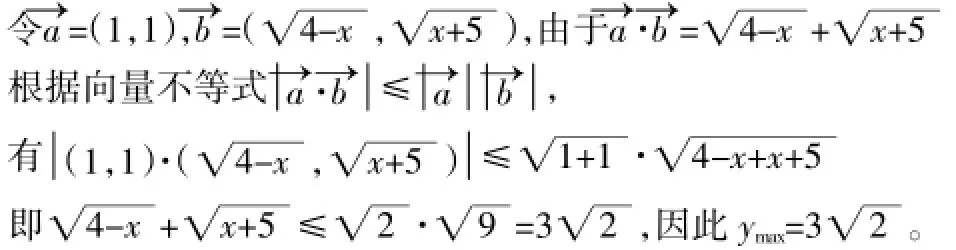
解法7构造对偶函数

另外，还可以利用对称性直观处理，利用柯西不等式等多种方法解决本题。

变式该题可以从已知求证变，也可以从隐藏条件、式子结构进行变式。

该题的变式题可以设计出如下一些，供大家参考使用：

总之，在寻求解题思路时，要让学生逐步学会怎样分析、怎样判断、怎样推理、怎样选择方法、怎样解决问题，通过充分暴露解题的思维过程，使学生的思维与教师的思维产生共鸣，使教师的思维为学生的思维过渡到科学的思维架起桥梁，变传授过程为发现过程。更重要的是在尝试、探索、发现的过程中，把失败的过程和失败到成功的过程暴露出来，使学生看到转变思维的方式、方法和策略，在体验和领悟中提炼出思想和方法，并逐步形成用思想方法进行思维的习惯，碰到问题能自觉地“往这方面想”，提升解题能力。

一题多解可以培养学生从不同角度思考问题的能力，找出题目中不同的关建点，从不同的关键点发散出去，用不同的方法解决问题变式题更是学好数学的一件法宝，通过变换已知条件或所求结论，可以衍生出相类似但又不同的各种题目，让学生在原题的基础上逐步去拓展，既不会出现思维掉链，又能让学生有发挥的空间。因此，让学生思考一题多解可以增强学生对原题条件的运用能力和探究能力，而变式题可以提高学生的创新思维能力，帮助学生培养发散思维。在教学中，教师就应该多用这样的方式来讲解课本上的例题，充分利用好教学资源，为学生带来更大的收获。

·编辑温雪莲