无人机非量测相机检校方法研究

2016-08-10田雷，马然

测绘通报 2016年7期

关键词：检校标志点物镜

田　雷，马　然

（1.吉林铁道职业技术学院，辽宁吉林130000；2.广州南方无人机技术有限公司，广东广州510000）

无人机非量测相机检校方法研究

田雷1，马然2

（1.吉林铁道职业技术学院，辽宁吉林130000；2.广州南方无人机技术有限公司，广东广州510000）

无人机搭载的非量测相机光学系统不稳定、畸变差大、内方位元素未知，难以满足大比例尺测图精度要求。本文通过建立高精度室内相机检校场，基于直接线性变换公式编写了非量测相机检校程序，根据解算得到的畸变参数对相机进行了改正，使之适用于大比例尺航空摄影测量成图，并通过实际项目验证了该方法的有效性。

无人机；非量测相机；室内检校场；相机检校

以无人机为平台的近地遥感系统，不受场地限制，数据采集实时、高效，可多角度快速获取地理空间信息，并广泛应用于大比例尺地形图测绘、国土与生态环境调查、动态监测与评估、数字城市及重大工程建设等领域。利用无人机对矿区进行多角度摄影，既可以获取地物地貌的高分辨率影像，也可获得建（构）筑物侧面的纹理影像用于提取建筑物的高度、面积、空间分布等信息，可为矿区拆迁区实时评估、房屋变化监测、规划管理等提供可靠的三维地理信息数据。

现在广泛使用的无人机大多体积小、载荷轻，难以搭载高精度扫描仪和数字化处理设备等，无人机平台通常搭载非量测相机作为传感器。由于非量测相机光学系统不稳定、内方位元素和畸变系数未知，获取的影像存在较大的光学畸变差，由此产生的像点位移将影响到空三加密精度及制图精度。因此，必须对非量测相机进行检校，才能满足地形图测绘的精度要求及后续的应用需求。

非量测相机检校常用方法有空间后方交会法、直接线性变换法等，本文采用后者进行相机检校。该方法是基于严格透视变换模型，通过求解线性方程组得到像点二维坐标与对应地面点三维坐标的转换模型，计算简单、检校精度高。

一、非量测相机检校方法

1.非量测相机检校内容

相机检校是通过相应参数改正模型和解算的光学畸变参数，恢复影像光束的正确形状，使其满足严格共线关系。无人机近地遥感系统非量测型相机检校内容包括:①像主点坐标（x0，y0）、主距f；②相机物镜光学畸变差。

相机镜头畸变差会造成像点坐标位移，使镜头中心、像点和对应的物点不能满足中心投影的光学共轭关系，从而降低影像的配准精度。光学畸变差包括径向、切向和偏心畸变（如图1所示）。

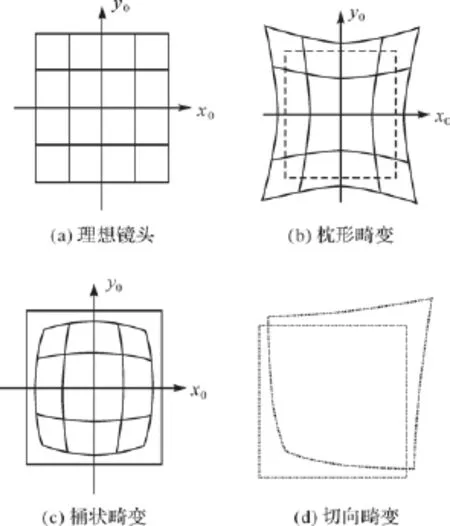
图1　物镜畸变差类型

物镜径向曲率误差造成像主点产生的径向偏移称为径向畸变，承影面上偏离几何中心越远，其产生的畸变就越大；相机透镜装配时，镜片组之间轴心不共线及成像版排列误差会产生切向畸变和偏心畸变。上述3种畸变共同导致了影像产生变形，其数学模型表示为

式中，（x0，y0）表示像主点坐标；（x，y）为像点坐标；k1、k2、p1、p2为镜头的畸变系数；r表示向径。

2.基于DLTD的相机检校方法

严格的中心投影共线条件方程为

由于非量测相机内方位元素未知，因此采用直接线性变换（DLT）公式进行解算。对式（1）进行改化，可得到适用于非量测相机检校的直接线性变换（DLT）公式

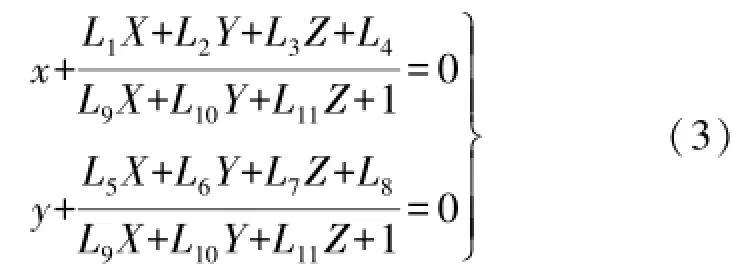
由于非量测相机物镜光学畸变差大，因此需要顾及物镜的径向变形、偏心变形及仿射变形，则附有畸变改正的直接线性变换公式可表示为

式（2）—式（4）中，（x，y）、（x0，y0）分别为像点坐标和像主点坐标；（X，Y，Z）为像点对应的地面点物方空间坐标；f为相机主距；（XS，YS，ZS）为摄站点的物方空间坐标；Δx、Δy为畸变改正参数，可表示为

径向畸变差（radial distortion）指像点沿径向方向偏离其准确位置，可用奇次多项式表达

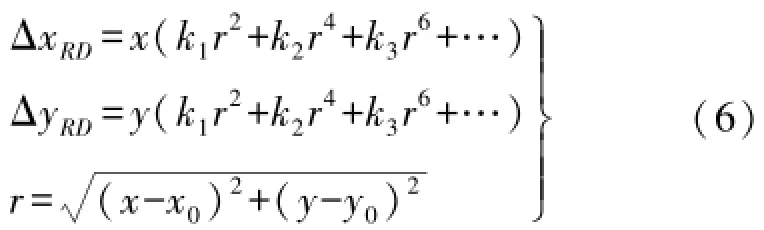
像点沿向径方向和正交于向径方向偏离的理想位置即为偏心误差（decentering distortion），向径误差称为非对称径向畸变；正交于向径方向的误差称为切向误差，其表达式为

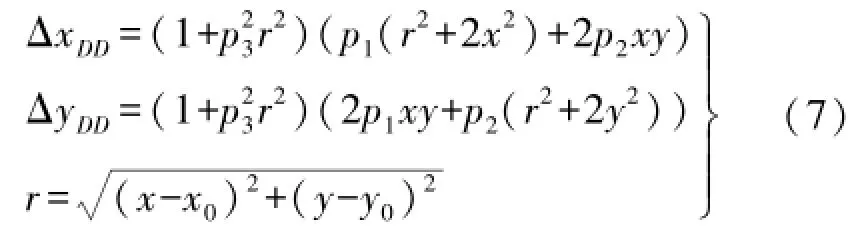
顾及镜头的径向畸变、偏心畸变及仿射变形，式（1）改化为

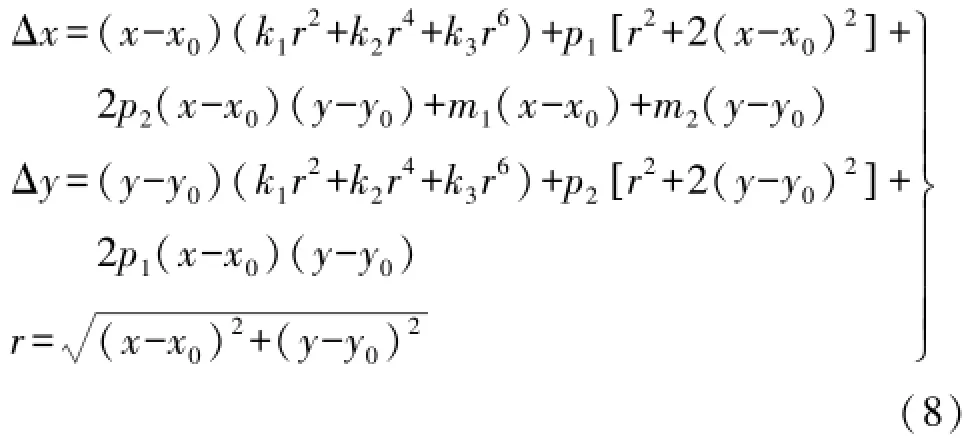
式中，m1、m2为成像面元的非正方形和不垂直性引起的仿射和剪切畸交换系数。利用该方法对非量测数码相机进行检校，可求得Li（i=1，2，…，11）及k1、k2、k3、p1、p2、m1、m2，通过进一步计算可得到内外方位元素。

二、相机检校

镜头畸变差校正方法为:建立一个高精度室内定标场，将待检校的非量测相机物镜的焦距设置在无穷远处，使主距f不变，从而保证内方位元素和物镜畸变系数稳定，然后对室内定标场进行摄影得到各个定标点的像点坐标，将标志点坐标根据共线方程反算出影像坐标（假定为无误差的像点坐标），最后由式（8）计算其畸变改正参数。

1.相机检校流程

非量测相机室内检校过程可分为检校场布设、检校参数求解及精度验证3个主要步骤，具体流程如图2所示。

图2　无人机非量测相机室内检校流程

2.相机及检校场

待检校的相机机型为Canon 5D MarkⅡ数码相机，相关参数见表1。

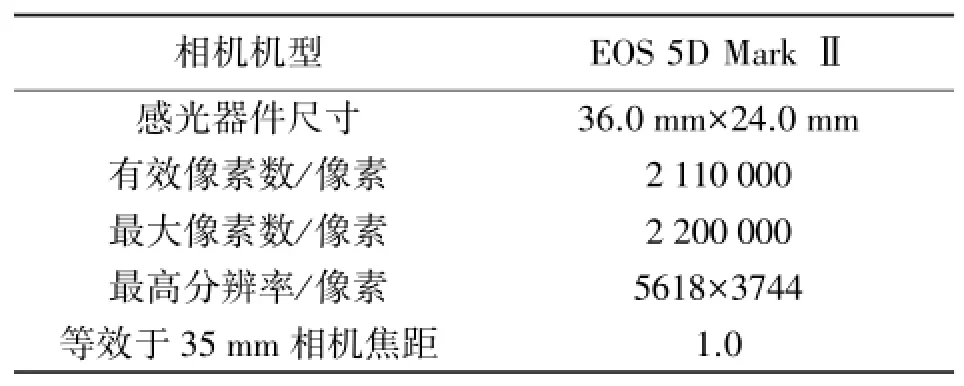
表1　检校相机的相关参数

室内检校场由4行7列共196个控制点（标志点）组成了控制网（如图3所示），建立的坐标系为平面坐标原点为观测墩A上的经纬仪竖轴的水平位置，高程基准点是以观测墩B上的经纬仪竖轴与横轴的交点高，X轴为观测墩A、B之间的连线在水平面上的投影，垂直于X轴向外并与X轴在同一水平面内的为Y轴，Z轴为铅垂方向（如图4所示）。控制网平面坐标原点由WILD T3光学经纬仪通过空间后方交会得到，各标志点的控制网平面坐标系的坐标通过空间前方交会获得，利用间接高程法测量各标志点的相对高程，控制点的三维坐标精度为0.3 mm。图3中，黑色标志点为精度评定时选用的验证点。

图3　室内检校场

图4　室内控制网坐标系

从196个标志点中选取20个点作为抽样样本，对标志点的测量精度进行评定，结果见表2。

由表2可知:196个标志点的三维坐标精度在0.3～0.7 mm之间，最大误差为0.632 mm。

3.检校结果

本文利用C++对Canon 5D MarkⅡ相机直接线性变换检校模型进行编程实现，获得其畸变参数改正值及内方位元素，见表3。

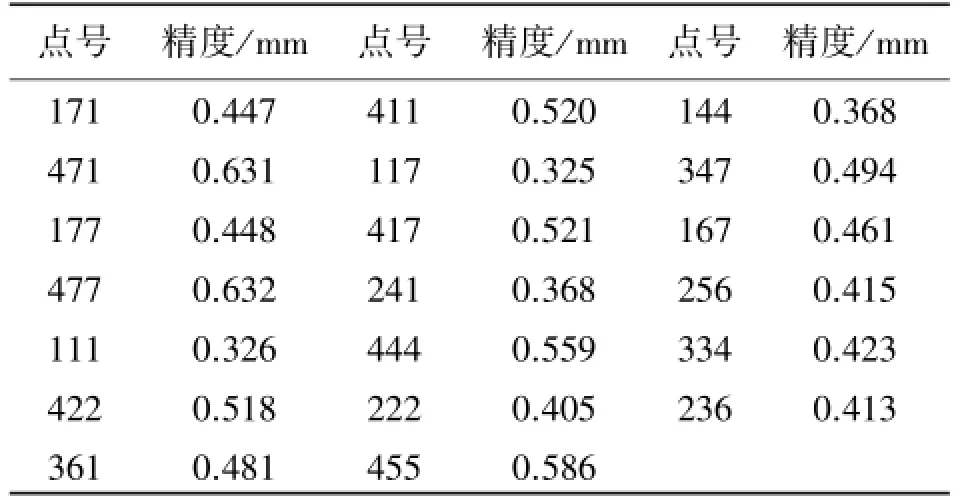
表2　验证点精度

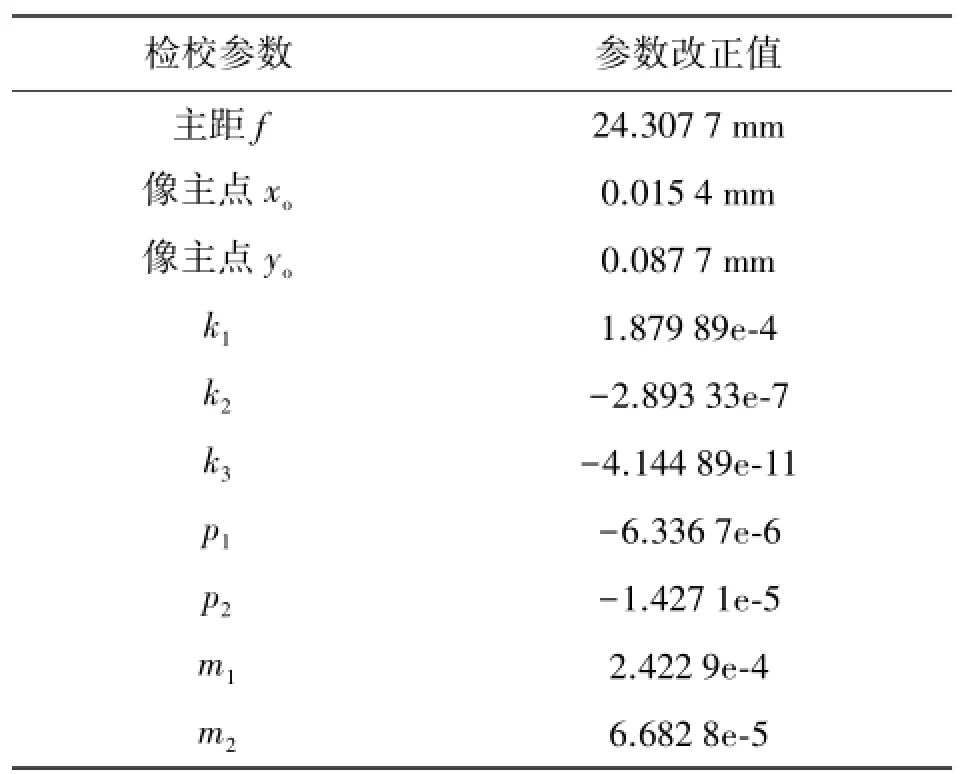
表3　相机检校参数及改正值

4.实例验证

在对非量测相机进行检校之后，用无人机搭载对测区进行航空摄影，获取了286张竖直摄影像片和520张倾斜摄影像片。无人机低空遥感获得的原始影像为5616×3744像素，经过本文建立的校正模型改正后为5716×3810像素，影像边缘的最大变形为100像素，变形比率为1.78%。将控制点坐标数据和无人机航摄影像数据进行空三加密，完成了摄影照片的无缝拼接并进行修饰，制作了满足制图精度要求的 1∶2000遥感正射影像图（DOM）及1∶1000倾斜影像全景图。