利用多LCD进行相机标定的模型及精度分析

詹总谦，彭　敏

（武汉大学测绘学院，湖北武汉430079）

利用多LCD进行相机标定的模型及精度分析

詹总谦，彭敏

（武汉大学测绘学院，湖北武汉430079）

鉴于现有利用LCD进行相机标定方法中所存在的缺点，本文提出了基于多LCD标定的方法，它很好地克服了仅用单LCD进行标定方法中存在的控制范围小、无深度信息等不足，同时对基于双LCD的标定方法进行了有效的拓展及改进。试验证明该方法是可行与有效的，可适用于更多种类的相机。

相机标定；多LCD；精度

相机标定作为从二维图像中准确获取物体量测信息的关键技术，一直是摄影测量与计算机视觉领域中的研究热点［1-2］。根据标定参考对象的维数，相机标定可分为4种方法［3］。其中基于二维平面的标定方法自 TSAI［4］在 1987年首次提出后，ZHANG［2］及STURM等［5］利用可随意移动的平面格网进行简化，方便灵活、成本低及精度高等特点就使其成为最为广泛使用的标定方法之一［2，5-7］。很多后续方法基于此进行改进，如 CHEN等［6］利用ZHANG［2］中的闭合解析解以确定所有相机内参数，但与ZHANG［2］精确测量平面格网点坐标不同，他们依据的是格网本身的几何性质，这也是利用二维平面进行相机标定所普遍使用的方法之一。而对于如何精确测定平面格网点坐标，许多学者也作了研究，在文献［8］等一些最近提出的标定方法中，标定精度已经达到亚像素级并可在使用中完全自动化。而Datta等［9］在其提出的方法中，对所有典型的格网表现形式（正方形、圆形、环形）进行了研究，通过在输入影像转化成的标准、无变形如正面平行拍摄的影像上量测格网点坐标并确定相机参数，该迭代方法相对于OpenCV［10］等基于ZHANG［2］的传统方法，精度有了很大的提高，在中等计算强度的情况下反投影误差减少了近50%。但该方法在图像发生模糊时可能失效，而在高标定精度要求的应用中，由于需要聚焦相对较小的平面图案模糊时常发生，基于此，Prakas等［11］提出先将正面平行图像通过自适应阈值分割成二值图像后，再对圆形中心点进行定位以剔除由于模糊和聚焦问题而引起的异常值。类似于文献［9］，该方法也是进行迭代优化，但对高分辨率图像其反投影误差减少了近57%。另外，考虑到现有基于平面进行相机标定的方法，通常需要在不同方向对平面拍摄多幅影像，并对拍摄角度要求严格，YANG等［12］对摄影方式也进行了改进。通过在同一方向只拍摄两张影像，该方法可有效获得相机内外参数（包括一些高阶畸变参数），但其迭代过程相当复杂。

对基于平面格网标定方法的改进已深入到方方面面，但作为最为常用、低成本的标定参考对象——附到合适平面上的打印平面格网，通常具有打印刻画、材料冷热收缩和压平等误差，这些都会影响相机标定的精度。虽然研究者们对此采取了诸多措施，包括使用高精度特制的平面格网或对方法本身进行改进，如Strobel等［7］提出可在平面格网控制点的真实坐标未知情况下进行相机标定的方法，有效避免了由打印刻画及坐标量测所带来的误差。然而，这些措施在方便实用或精度上尚难达到统一。

2002年，NOMA等［13］第一次指出LCD可用于相机标定，但其并没有进行试验和分析。随后在文献［12］及［14—18］等研究中，基于LCD进行相机标定的方法才逐渐被付诸实践。高精度标定结果证明了其相对利用打印纸张进行标定方法的优越性: ①LCD作为标定参考对象，通常由于成熟的制造工艺，具有很高的平面几何精度；②更加方便、准确，只需简单的程序就可自动绘制二维平面格网及获得控制点在三维空间中的实际坐标［14-15］。

如今基于LCD标定的方法通常只使用单个LCD，虽然ZHANG等［18］实现了利用3个LCD以拍摄一张影像来对全景摄像机进行标定的方法，但遗憾的是该方法并没有说明如何确立LCD之间的关系，并且忽略了相机本身的畸变。由于单个LCD尺寸有限，使得拍摄时相机不能距离LCD太远。同时不能提供深度信息，造成相机标定结果中的主距值存在一定的偏差。虽然这些不足在基于双LCD进行标定的方法［16］中已经得到了改进，但本文仍希望通过扩展其模型，以使其控制场范围更大，从而适用性更加广泛。试验证明基于多LCD进行相机标定的方法是可行与有效的。下面将对其三维控制场、标定模型及方法进行详细说明。

一、三维控制场

基于多LCD相机标定的三维控制场类似于基于双LCD标定的三维控制场［16］，也由两部分组成。但对于硬件部分，这里包含了一个主LCD及两个或两个以上的辅LCD。并且为了提供适当的深度信息，仍将每个辅LCD与主LCD近似平行放置，但进一步缩小了夹角（5°左右），同时主辅平面在Z方向上保持约10 cm的间距。这种摆放方式很好地解决了在基于双LCD标定中角度（约20°～30°）过大引起的难题，可进一步提高标定的精度。如图1（a）所示，对相机S1而言，受LCD可视角度影响，辅LCD （L2）上的最大的控制点入射角 θ将远远大于主LCD（L1）的最大控制点入射角Φ，因此造成L2上控制点成像对比度低、变形大。但很显然的，图1（b）中的摆放方式（存在一个小角度，近似平行）可在两个LCD之间取得成像光线入射角的平衡，使得主辅平面上的控制点都获得较好的成像质量。

图1　基于双 /多LCD的相机标定中主LCD与辅LCD间的摆放关系

至于软件部分，由于试验证明通过颜色识别可能无法自动识别关键圆点的初始位置。这是因为某些相机必须通过设置特殊的光圈和景深才能拍摄到清晰的影像，此时关键圆的颜色会出现异常；而当拍摄距离较远时，LCD的成像较小，此时外界的颜色也可能影响自动识别。因而采用编码标志点来代替以前使用的特殊颜色点，以便每张影像上的坐标系及LCD间的主辅关系可被完全自动识别出来。同样的，类似文献［16］，仍然认为辅坐标系和主坐标系间存在绝对定向关系，即辅坐标系可通过主坐标系的平移、旋转和缩放进行确定。图2是基于4个LCD进行相机标定的系统。

图2　含有4个LCD的标定系统（作为基准点的编码标志点在每个LCD的中心）

二、标定模型

根据双LCD标定的数学模型［16］，可以很容易地扩展出基于多LCD的标定模型。由于每增加一个LCD就相应增加一组绝对定向参数，而每个辅坐标系与主坐标系间的关系可通过如下公式给出

式中，下标（i=1，2，3，…）表示第i个辅LCD；（X，Y，Z）表示辅平面格网点经过绝对定向后在主坐标系下的坐标；（X′i，Y′i，Z′i）表示辅平面格网点在其自身坐标系下的坐标（Z′i≡0）；λi表示辅坐标系相对主坐标系的比例尺缩放因子；（ΔXi，ΔYi，ΔZi）表示辅坐标系原点相对主坐标系原点的平移量；｛Aji，Bji，Cji（j=1，2，3）｝是由辅坐标系相对主坐标系的3个旋转角度构成的9个方向余弦。

由于主平面格网点对应的数学模型与基于单LCD的标定模型一致，那么将式（1）代入文献［17］中的式（2）就可得到辅平面格网点在主坐标系下的共线方程

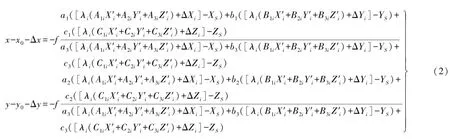
式中，（x0，y0）为相机的主点坐标；（Δx，Δy）为当前外方位角元素φ，ω，κ组成的旋转矩阵。像点（x，y）的畸变差；f为主距；（XS，YS，ZS）为摄站利用泰勒级数公式对式（2）进行展开，便可得到点的物方空间坐标；｛ai，bi，ci，i=1，2，3｝为像片3个辅平面格网点在主坐标系下对应的线性化误差方程

式中，vx和vy为像点坐标观测值的改正数；x0和y0畸变参数。为将未知数的初值代入共线方程后所得到的像点坐那么，若基于N个LCD进行标定，则可以选取标估计值；k1和k2为径向畸变参数；p1和p2为偏心其中一个LCD作为主坐标系，其余的N-1个LCD作为辅坐标系，此时包含（N-1）×7个绝对定向参数，它们在平差时相互独立，对应的误差方程式系数与基于双LCD的数学模型一致。

如前所述，主平面格网点与基于单LCD的标定具有相同的数学模型，那么结合其线性化误差方程与式（3），便可得到整个标定模型。

三、试验及精度分析

将所有的LCD近似平行放置但不共面，采用与基于双LCD标定一致的拍摄方法，就可以进行相机标定，其过程与文献［16］近乎相同，但由于存在两个或两个以上的辅坐标系，导致初值计算及平差过程更为复杂。

按照上述标定过程，以含有4个LCD的相机标定试验为例，来验证基于多LCD标定方法的可行性。因辅平面格网的实际空间坐标并非已知，可通过主平面格网上检查点的精度及辅平面格网上的点间距离误差来评价试验结果。为了进行对比分析，利用单LCD标定方法对同一相机进行了标定。

标定精度见表1。需要说明的是当采用4个LCD进行相机标定时，计算得到的平均深度是相对于主LCD而言的。从表1可以看出，随着距离的增大，基于LCD标定方法的精度都会相应降低（对比文献［16—17］中的标定结果）。然而，与基于单LCD相机标定的试验结果相比，采用多LCD进行相机标定的方法仍是可行有效的，原因如下:①两者之间的单位权中误差相差很小，为0.015个像素；②检查点的平面和深度精度也许相对较低，但其需要的影像数相对更少，并且具有很高的距离精度。

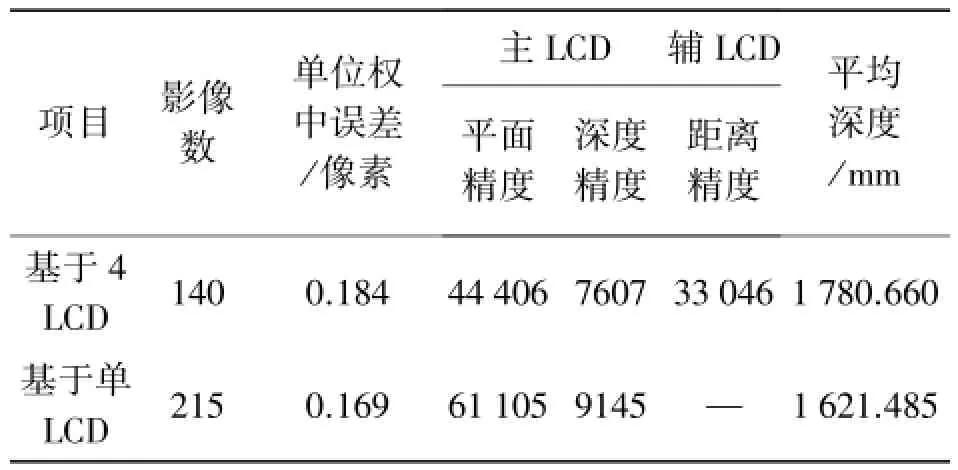
表1　基于单/多LCD标定的结果（相对精度）

为了进一步说明问题，将多LCD相机标定得到的参数代入基于单LCD标定方法中，并把它们当作真实值，从而可由检查点精度获得该方法的实际测量精度。从表2可知，实际测量精度与表1中基于单LCD标定得到的精度相当，再次证明该方法是可行有效的。

表2　标定参数的实际测量精度

四、结束语

通过进一步扩展基于双LCD的标定模型，本文详细叙述了如何利用多LCD进行相机标定的方法。试验证明它是可行有效的，且精度很高。对比于文献［16］和［17］，基于多LCD的相机标定不仅为基于单LCD的标定方法提供了深度信息，同时也实现了更大的影像控制范围，因而它可适用于更多种类的相机，特别是对大幅面、高分辨率或者广角（鱼眼镜头）的专业相机。

［1］ LUCCHESE L.Geometric Calibration of Digital Cameras through Multi-view Rectification［J］.Image and Vision Computing，2005，23（5）:517-539.

［2］ ZHANG Z Y.A Flexible New Technique for Camera Calibration［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22（11）:1330-1334.

［3］ ZHANG Z Y.Camera Calibration with One-dimensional Objects［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26（7）:892-899.

［4］ TSAI R Y.A Versatile Camera Calibration Technique for High-accuracy 3D Machine Vision Metrology Using Offthe-shelf TV Cameras and Lenses［J］.IEEE Journal of Robotics and Automation，1987，3（4）:323-344.

［5］ STURM P F，MAYBANK S J.On Plane-based Camera Calibration:A General Algorithm，Singularities，Applications ［C］∥ IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Fort Collins:IEEE，1999.

［6］ CHEN A H，HE B W.A Camera Calibration Technique Based on Planar Geometry Feature［C］∥14th International Conference on Mechatronics and Machine Vision in Practice.Xiamen:IEEE，2007.

［7］ STROBL K H，HIRZINGER G.More Accurate Camera and Hand-eye Calibrations with Unknown Grid Pattern Dimensions［C］∥ IEEE International Conference on Robotics and Automation.Pasadena:IEEE，2008.

［8］ LIN Y，LU N，LOU X，et al.A Novel Approach to Subpixel Corner Detection of the Grid in Camera Calibration ［C］∥2010 International Conference on Computer Application and System Modeling（ICCASM）.Taiyuan: IEEE，2010.

［9］ DATTA A，KIM J S，KANADE T.Accurate Camera Calibration Using Iterative Refinement of Control Points ［C］∥ 2009 IEEE 12th International Conference on Computer Vision Workshops（ICCV Workshops）.Kyoto:IEEE，2009.

［10］ BRADSKI G.Learning-Based Computer Vision with Intel’s Open Source Computer Vision Library［J］.Intel Technology Journal，2005，9（2）:119-130.

［11］ PRAKASH C D，KARAM L J.Camera Calibration U-sing Adaptive Segmentation and Ellipse Fitting for Localizing Control Points［C］∥2012 19th IEEE International Conference on Image Processing（ICIP）.Orlando:IEEE，2012.

［12］ YANG B，LI H，WU M F，et al.A Novel Method for Camera Calibration Based on Micro Plane Grid［C］∥2013 21st International Conference on Geoinformatics （GEOINFORMATICS）.Kaifeng:IEEE，2013.

［13］ NOMA T，OTANI H，ITO T，et al.New System of Diband Satellite SAR Interferometry［J］.Landslides，2005 （2）:193-201.

［5］ BERNARD I G，RICC I P，COPPI F.A Ground Based Microwave Interferometer with Imaging Capabilities for Remote Measurements of Displacements［C］∥3rd International Geotelematics Fair（GlobalGeo）.Barcelona，Spain:［s.n.］，2007:20-23.

［6］ 廖明生，林珲.雷达干涉测量—原理与信号处理基础［M］.北京:测绘出版社，2003.

［7］ CUMMING I G，WONG F H，RANEY R K.A SAR Processing Algorithm with No Interpolation［C］∥Proceedings of the International Geoscience and Remote Sensing Symposium.［S.l.］:IGARSS，1992:376-379.

［8］ 邱志伟，张路，廖明生.一种顾及相干性的星载干涉SAR成像算法［J］.武汉大学学报（信息科学版），2010，35（9）:1065-1068.

［9］ 何敏，何秀凤.合成孔径雷达干涉测量技术及其在形变灾害监测中的应用［J］.水电自动化与大坝监测，2005.29（2）:45-48.

［10］ CHANG C Y，CURLANDER J C.Doppler Centroid Ambiguity Estimation for Synthetic Aperture Radars［C］∥Proceedings of the International Geoscience and Remote Sensing Symposium.［S.l.］:IGARSS，1989:2567-2571.

［11］ 刘国祥，陈强，丁晓利.基于雷达干涉永久散射体网络探测地表形变的算法与实验结果［J］.测绘学报，2007，36（1）:13-18. gital Camera Calibration，DC-1000［C］∥ ISPRS SymPosium.Corfu:ISPRS，2002.

［14］ 詹总谦，张祖勋，张剑清.基于LCD平面格网及有限元内插模型的相机标定［J］.武汉大学学报（信息科学版），2007，32（5）:394-397.

［15］ SONG Z，CHUNG R.Use of LCD Panel for Calibrating Structured-Light-Based Range Sensing System［J］. IEEE Transactions on Instrumentation and Measurement，2008，57（11）:2623-2630.

［16］ 詹总谦，张祖勋，张剑清.基于双LCD的相机标定模型及其精度分析［J］.测绘通报，2009（11）:14-20.

［17］ ZHAN Z Q.Camera Calibration Based on Liquid Crystal Display（LCD）［J］.The International Archives of the Photogrammetry，Remote Sensing and Spatial Information Sciences，2008（37）:15-20.

［18］ ZHANG L，ZHANG J，HU Y.A Practical Method for Calibrating Omnidirectional Cameras Using LCD Panel ［C］∥ International Conference on Information and Automation.Zhuhai:IEEE，2009.

Model and Accuracy Analysis for Camera Calibration Using Multiple LCDs

ZHAN Zongqian，PENG Min

10.13474/j.cnki.11-2246.2016.0215.

P23

B

0494-0911（2016）07-0017-04

2015-07-13；

2015-10-20

国家科技支撑项目（2012BAJ23B03）

詹总谦（1987—），男，博士，副教授，研究方向为摄影测量与计算机视觉。E-mail:zqzhan@sgg.whu.edu.cn

彭 敏

引文格式：詹总谦，彭敏.利用多LCD进行相机标定的模型及精度分析［J］.测绘通报，2016（7）:17-20.