基于短基线的北斗动动定位方法的几点探讨

章　畅，汪　捷，徐冠楠

（海军工程大学导航工程系，湖北武汉430033）

基于短基线的北斗动动定位方法的几点探讨

章畅，汪捷，徐冠楠

（海军工程大学导航工程系，湖北武汉430033）

针对北斗动动定位中接收机信号易受遮挡导致无法实时准确进行相对基线测量的问题，本文提出了一种利用惯性测量信息辅助动态模糊度的解算方法。通过载波相位差分观测方程与惯导观测方程组合的方式，讨论在共视卫星数目在不同观测条件下的模糊度求解方法。在此基础上，建立了基于惯导信息辅助的动动定位组合试验系统，利用车载试验进行了相关测试。结果表明，在可视卫星数目较少的情况下，BDS定位精度效果优于GPS；利用IMU信息辅助提高了定位连续性和精度。

北斗动动定位；惯性测量信息；动态模糊度；车载试验

传统的动动定位方程大都基于载波相位双差模型，在卫星数目为N的情况下未知数个数为N-1个模糊度和3个坐标未知数。而根据观测方程求解模糊度的特点，在观测历元较少时，利用如LAMBDA法、最小二乘法等法解算模糊度时会出现法方程秩亏的现象，导致无法顺利求解模糊度。因此如何解决复杂观测条件下解算动态模糊度的问题成为研究领域的热点和难点。针对双频观测模型，本文提出利用宽巷组合的模式，通过分步消元的方法进行模糊度求解。

一、动态模糊度解算

BDS动动定位通常采用双差观测模型，现在此基础上，通过IMU观测信息融合辅助。在可视卫星数目大于4颗时，既可以根据传统的最小二乘法求解模糊度，也可以通过滤波法求解模糊度，不作详细讨论。现着重讨论可见卫星数目或4颗两种条件下的模糊度解算方法。

在可见的卫星数目小于4颗时，由BDS观测方程可知未知数个数大于观测方程个数，故无法求解模糊度和基线向量。

假设INS短时间内导航输出的三维位置为RINS，在可见卫星数目小于4颗时，分别联立伪距、载波相位以及INS输出的位置并作线性化可以得到如下组合观测方程

需要注意的是，由于可见卫星数目不足4颗的原因，导致模糊度的变量个数小于4个，有些情况甚至只有1个，对上述组合方程利用最小二乘法解算，便可以得到模糊度浮点解，记为 N21，N21，…，Nn1（2 ≤n≤4）。

设惯导输出的姿态矩阵为Cb，RIb为利用惯导输出信息解算得到的基线向量，Rb为两个动态站搭载的卫导接收机天线构成的基线在坐标系中的向量，φ为惯导平台误差角向量。利用本文算法得出的由惯导输出信息求得的基线向量为

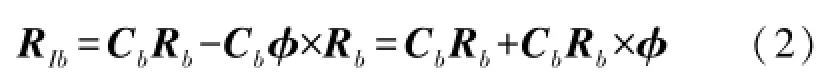
通过组合滤波输出的方差阵可以得出利用惯导位置计算的基线向量方差阵为

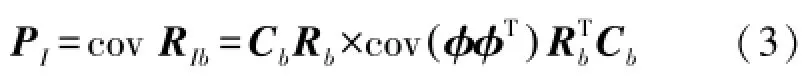
因此，由双差载波相位观测方程与惯导输出的基线向量和方差矩阵得出模糊度向量为

二、试验验证

2015年2月10日于武汉市解放大道古田路一段足够长的15°斜坡上开展测试。其中接收机均为双频Novatel公司的BDS+GPS差分型。

试验过程中，移动站车辆从一个15°左右的坡上向下驶向移动基站车辆，移动基站车辆在坡下做低速运动。接收机的定位模式设置为BDS+GPS组合定位，卫星截止高度角设置为15°，数据更新频率为1 Hz，对试验数据实时保存，整个试验过程时长为4 h。

事后对整个试验过程采集数据进行处理，总时长大约1 h，记为S1，如图1所示。

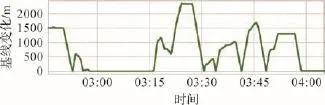
图1　试验过程相对基线变化

事后进行BDS单历元与GPS单历元定位分析。首先对试验采集的原始数据进行双频事后处理，其中GPS采用L1和L2频率，BDS采用B1和B2频率，处理方法和上述单历元定位方法一致。图2分别给出了在S1时段的卫星数变化，利用B1（L1）搜素最佳模糊度的Ratio值和定位误差PosError，记为σ，计算方法如下σ=^σ0·PDOP式中，^σ0为验后的单位权重误差；PDOP为相对定位的几何精度衰减因子。通常，往往用σ的大小来检验定位结果的正确性。在短基线（小于10 km）情况下，σ一般小于0.05 m，如果出现大于0.10 m的情况，则表明解算结果错误。S1时段指标如图 2所示。

为更好地定量分析，对上述结果进行了统计计算（见表1）。

图2　试验过程单历元解算结果

表1　试验过程中BDS和GPS相关指标统计结果

从表1可以看出，BDS平均可视卫星数在整个试验过程中多于GPS，并且BDS所有历元都可以完成正常解算，而GPS在S1时段有38个无法解算；Ratio值方面，一般而言，Ratio值大于3认为模糊度固定成功，由表1可见，BDS对B1模糊度搜索的Ratio平均值大于GPS搜索L1的模糊度Ratio平均值，且BDS的模糊度固定成功率高于GPS；从pos值来看，BDS平均值小于5 cm的历元均大于99%，而相应的GPS只有96%左右。

对整个过程的所有试验数据进行95%的置信概率统计精度分析，可以得到BDS系统的水平、垂直和三维定位精度（见表2）。

表2　BDS系统定位精度结果

1.加入IMU信息的辅助分析

为测试加入IMU信息对BDS动动定位精度的效果，现对流动站采集的IMU信息和BDS差分信息进行滤波解算，得到的各历元基线矢量分量和长度变化如图3所示。

将上述解算结果与商业动态组合处理软件Interial explorer（可解算GPS+IMU组合信息，解算精度高）的结果进行比较，得到其偏差如图4所示。

图3　BDS+IMU滤波解算的分量变化

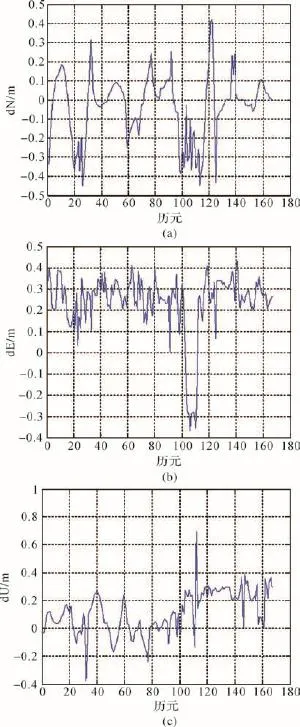
图4　BDS+IMU单历元解与IE结果差值序列

对试验结果进行95%置信概率的统计精度分析，其中n=180，利用相关公式得出N、E、U向的精度见表3。

表3　BDS+INS动动定位精度结果　m

结合表2和表3可以看出，经过IMU信息辅助的BDS动动定位的水平精度可以达到0.224 m，垂直定位精度为0.328 m（2σ，95%），优于原BDS单系统动动定位效果。

三、结束语

通过本文北斗动动定位试验分析可知，可视卫星数目直接影响动动定位的精度和效果，在可见卫星数目较少的情况下，BDS动动定位精度优于GPS；同时提出了利用IMU信息辅助动动定位的方法并进行了相关测试，结果表明，经过IMU辅助之后的BDS动动定位较单BDS动动定位在精度和实时性方面都有所改善。

［1］ 史琳.GPS整周模糊度及其在姿态测量中的应用研究［D］.武汉:武汉理工大学，2008.

［2］ 刘立龙.动态对动态GPS高精度定位理论及其应用研究［D］.武汉:武汉大学，2005.

［3］ 喻国荣.基于移动参考站的GPS动态相对定位算法研究［D］.武汉:武汉大学，2003.

［4］ 葛茂荣，过静珺，谢宝童.动态对动态GPS实时差分定位［J］.工程勘察，1998（4）:55-57.

［5］ 葛茂荣，过静珺.GPS相对导航在航天器交会对接中的应用［J］.测绘通报，1998（5）:6-7.

［6］ 刘广军，曾纪斌.GPS动态相对导航用于航天器交会对接的研究及其OTF解算方法［J］.飞行器测控学报，2000，19（2）:86-93.

［7］ 阳仁贵，袁运斌，欧吉坤.相位实时差分技术应用于飞行器交会对接研究［J］.中国科学:物理学力学天文学，2010，40（5）:651-657.

［8］ LUO N.Precise Relative Positioning of Multiple Moving Platforms Using GPS Carrier Phase Observables［D］. Calgary:University of Calgary，2001.

［9］ HEMRANN B R，EVANS A G，LAW C S，et al.Kinematic on the Fly GPS Positioning Relative to a Moving Reference［J］.Journal of the Institute of Navigation，1995，42（3）:487-501.

［10］ JONGE P D，TIBERIUS C C J M.The LAMBDA Method for Integer Ambiguity Estimation:Implementation Aspects［C］∥LGR-Series Delft:the Delft Geodetie Computing Centre，1996:1-59.

Some Research on BeiDou Kinematic-to-kinematic Positioning Method Based on Short Baseline

ZHANG Chang，WANG Jie，XU Guannan

10.13474/j.cnki.11-2246.2016. 0214.

P228

B

0494-0911（2016）07-0014-03

2015-08-14；

2016-05-18

总装“十二五”预研基金项目（9140A24020713JB11001）；装备预研基金（51324040103）

章 畅（1988—），男，硕士，主要研究方向为北斗导航定位以及测控遥感等。E-mail:626852648@qq.com

引文格式：章畅，汪捷，徐冠楠.基于短基线的北斗动动定位方法的几点探讨［J］.测绘通报，2016（7）:14-16.