空心弹空气阻力特性计算与数值仿真
2016-08-10王雨时张志彪
张 浩,闻 泉,王雨时,张志彪
(南京理工大学 机械工程学院,南京 210094)
空心弹空气阻力特性计算与数值仿真
张浩,闻泉,王雨时,张志彪
(南京理工大学 机械工程学院,南京210094)
摘要:应用Fluent软件仿真空心弹典型设计方案简化模型的空气动力流场,得到了其阻力系数与马赫数的关系,运用Matlab软件数值求解空心弹外弹道质心运动微分方程组,得到了弹道顶点和落点诸元。将以上所得阻力系数和弹道诸元与公式计算结果进行对比表明:在来流马赫数为2.0~4.4时,无弹带结构的简化空心弹模型用两种方法所得外弹道诸元结果相差很小;弹丸头部前缘厚度在可信区间内对阻力系数影响较小,但弹带结构对阻力系数的影响较大;工程设计时,受弹带结构影响,某空心弹简化模型阻力系数计算公式不太适合于工程问题求解,此时应以数值仿真为佳。
关键词:空心弹;仿真;公式;阻力系数;外弹道
本文引用格式:张浩,闻泉,王雨时,等.空心弹空气阻力特性计算与数值仿真[J].兵器装备工程学报,2016(7):5-11.
Citation format:ZHANG Hao,WEN Quan,WANG Yu-shi,et al.Theoretical Calculations and Numerical Simulation on Air Resistance Characteristics of Hollow Projectile[J].Journal of Ordnance Equipment Engineering,2016(7):5-11.
空心弹(Hollow Projectile)相对于实心弹而言,属于超音速旋转稳定弹药,其飞行部分最简单的形式就是一个中空薄壁圆管,因此又称为管式弹(Tubular Projectile)。空心弹沿弹丸轴线是一通孔,几乎所有靠近圆管前端面的空气都从孔中流过,而外表面的空气理论上保持平行几乎未受扰动。与实心弹相比,空心弹的头部激波阻力和尾部涡流阻力大大减小。射击试验表明空心弹阻力系数一般可降为普通弹的1/2到1/3。另外,空心弹还具有速度高、飞行时间短、命中精度高以及对目标侵彻能力强等一系列优异特性[1-3]。
从上世纪70年代初以来,世界各国广泛开展了空心弹的基础理论研究和应用开发研究,所研究的口径从5.56 mm一直到105 mm(坦克炮训练弹),重点是7.62 mm(枪弹)和20 mm(炮弹),很多著名的科研机构和军火商都都在积极参与。我国空心弹技术的研究工作起步于上世纪70年代末,但基本上属于对国外研究成果的试验验证。近年来,随着计算流体力学的发展,应用流体动力学仿真软件对空心弹流场进行数值模拟的技术已逐渐成熟。南京理工大学高旭东等[4-5]应用高精度、高分辨率的隐式有限体积TVD格式,结合分区算法,数值模拟了气流入口收敛面积比不同的空心弹内外流场结构,证实存在使弹丸阻力最小的气流入口面积比。任登凤[6]采用非结构网格的LU-S GS隐式算法计算三维Euler方程,数值模拟了不同马赫数及不同攻角下某空心弹的绕流流场,分析了流场波系结构及其升力和阻力特性。钱吉胜等[7]研究了空心弹在不同马赫数与攻角条件下的流场结构,表明虽然空心弹表面摩阻增加,但其结构带来的波阻与压阻降低使总阻力仍然较小。李艳玲[8-9]、黄振贵[10]等对空心弹的流场结构进行优化,得到了在具有相同内径、外径以及弹丸长度条件下阻力系数最小的空心弹几何结构。
目前,关于流体动力学问题的计算机仿真技术已比较成熟,结果较为可信。但就目前的计算机硬件普及程度,仍嫌效率不足。有必要利用仿真手段验证以往理论研究成果的适应性和准确性。基于此,本文应用Fluent软件仿真研究空心弹头部前缘厚度微小变化以及弹带对其阻力系数的影响,并结合混合锥形空心弹阻力系数理论计算公式,对比分析数值仿真结果与理论公式计算结果的差异,为空心弹型号产品的设计和开发提供技术基础。
1空心弹阻力系数计算公式
文献[11]和文献[12]根据锥-柱组合体常规弹丸阻力系数计算公式推导了外锥形空心弹和内锥形空心弹阻力系数表达式;文献[13]进一步给出了混合锥形空心弹的阻力系数计算公式。
混合锥形空心弹简化模型如图1所示,其中Di为入口直径,D0为弹径,Dt为喉部直径,θ0为外楔角,θi为内楔角。其阻力系数计算公式为:
(1)
其中
(2)
CDf= 4(1 + 0.15M2)-0.432×
(3)
CDb=(0.633 1-0.332 57M+0.066 19M2-
(4)
式(2)中
式(1)~(4)中L为弹丸全长;Cp为头部压阻系数;CDp0、CDp1分别为内、外楔压阻系数;CDf为摩阻系数;CDb为底部压阻系数。头部压阻系数表达式和摩阻系数表达式均是根据计算流体力学理论推导而来的,而底部压阻系数表达式是根据105 mm空心弹[14]模型风洞试验结果拟合得到的。此外,使用该公式时有如下假设前提:
a)两维流体流动;
b)弹丸攻角为零;
c)附在弹丸前缘上的激波为斜激波。

图1 空心弹结构示意图
2空心弹流场的数值模拟
2.1数值方法
湍流模型采用常用于航空领域的Spalart-Allmaras单方程模型,运用雷诺平均Navier-Stokes方程对该湍流模型求解,以数值模拟空心弹流场。
雷诺平均Navier-Stokes方程:
(5)
(6)
(7)
使用有限体积法对控制方程进行空间离散,控制节点取网格单元中心。方程的对流项采用混合通量差分(Advection Upstream Splitting Method)格式,而粘性项采用两阶中心差分格式,时间项则取二阶R-K格式[8-9]。
2.2弹丸模型及网格
工程实践中,受工艺等条件的约束,空心弹结构不可能与图1所示空心弹结构完全相同,图2为有弹带的空心弹结构(假设弹带与弹体一体,并且不考虑身管阳线对弹带切槽的影响)。以图2所示空心弹模型为对象,仿真研究空心弹头部前缘厚度的微小变化以及弹带对其阻力系数的影响,仿真模型具体结构参数如表1所列,其中模型1与图1所示空心弹简化模型完全相同,模型2~模型8增加了弹丸头部前缘厚度t或增设了弹带。
图2 带有弹带的空心弹模型

表1 空心弹模型具体参数
使用ANSYS Workbench 14.0中的Fluent模块建立弹体的仿真简化模型,取空气计算域长度为10倍弹长、直径为20倍弹径。为了保证计算收敛性和计算结果准确性,采用笛卡尔网格法对计算区域进行网格划分。笛卡尔网格相对于结构网格、非结构网格具有如下优势:网格生成简单,易于实现自动化,具有更强的自适应能力,更适合于处理复杂几何外形的绕流和由于物体运动或变形等产生的非定常问题。弹丸周围空气域网格如图3所示。

图3 弹体周围空气域网格
设置计算域空气模型为ideal-gas,选取Sutherland粘度定律。对于边界条件的设定,取壁面边界为无滑移绝热边界,外边界取压力远场进口与出口边界,大小为一个标准大气压,温度为300 K,来流马赫数取为1.2~4.6。选取基于密度的求解器求解。
3结果与讨论
3.1流场数值模拟结果与分析
由于篇幅有限,以下只列出马赫数为1.6、1.8、2.0、4.0时,弹丸(模型1)周围压力等值线和速度等值线图,如图4~图11所示。

图4 4.0 Ma时压力等值线图

图5 4.0 Ma时速度等值线图
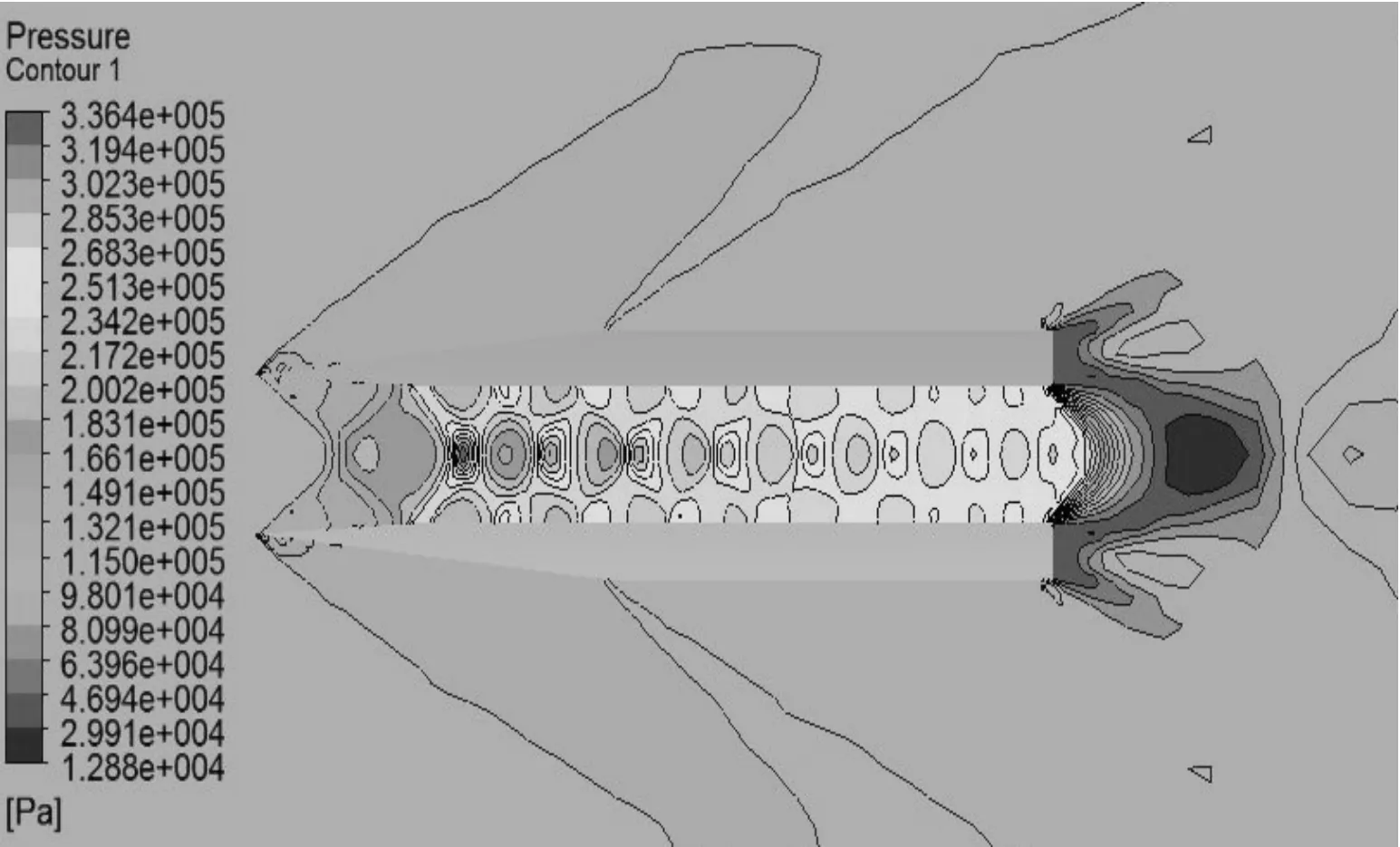
图6 2.0 Ma时压力等值线图

图7 2.0 Ma时速度等值线图
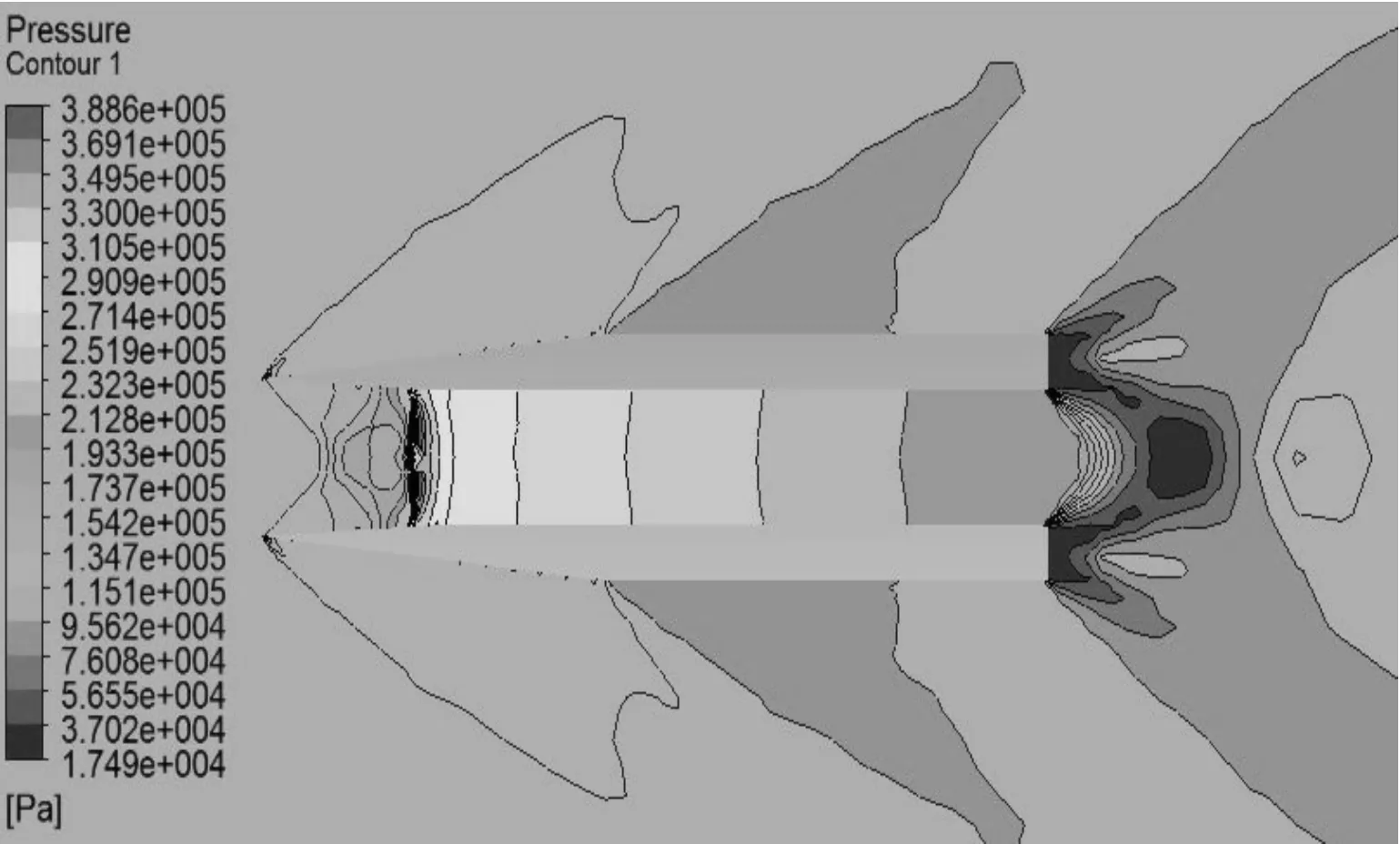
图8 1.8 Ma时压力等值线图

图9 1.8 Ma时速度等值线图
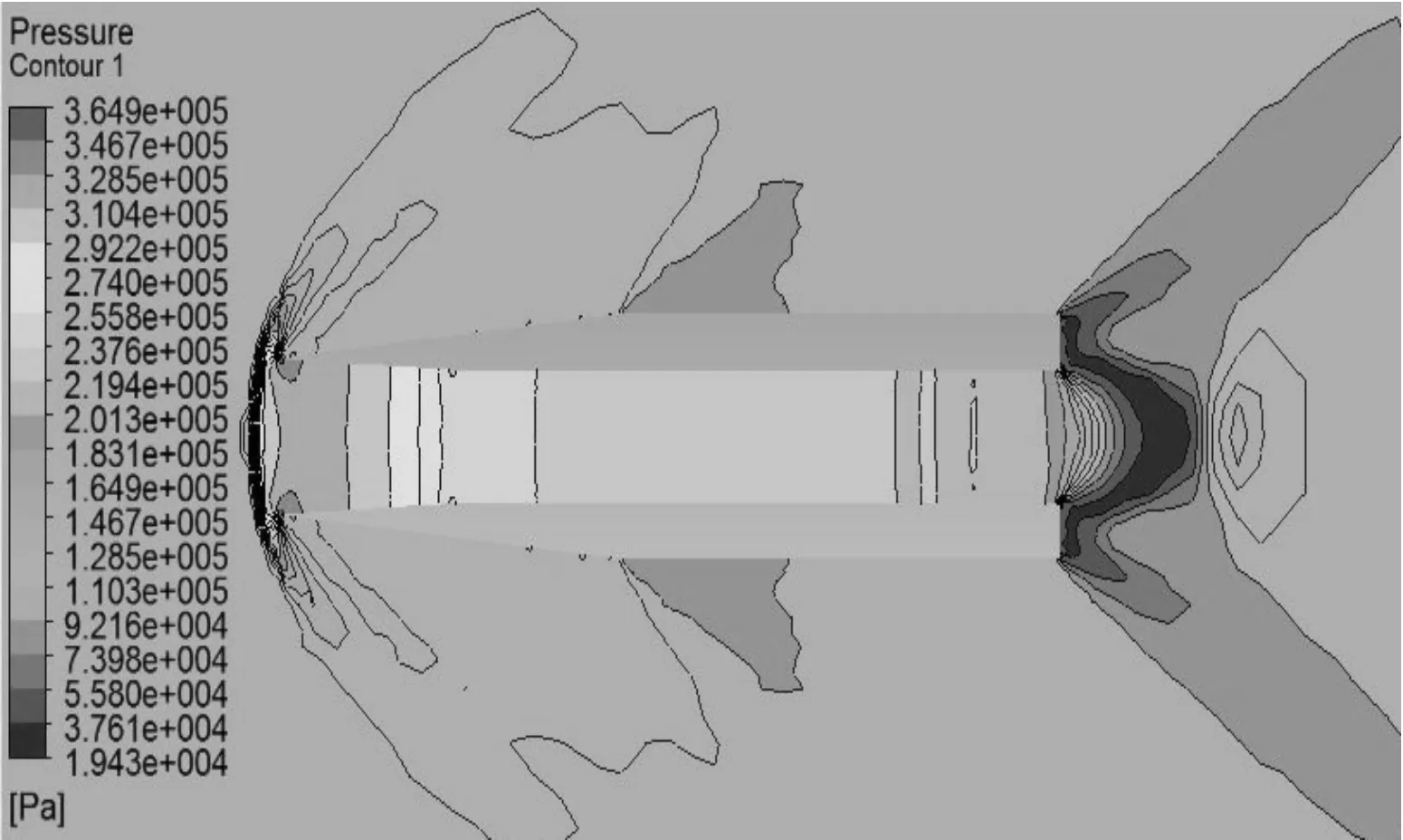
图10 1.6 Ma时压力等值线图

图11 1.6 Ma时速度等值线图
对比不同马赫数下空心弹周围流场的压力等值图和速度等值图可知:
1) 马赫数为2.0以上时,空心弹流场波系结构具有相似性,在弹丸的尖头部分首先产生斜激波。由于弹丸侧面无拐角,所以斜激波后形成的压缩波一直传递到弹尾;在空心弹内部,由尖头部分产生的斜激波流入空心弹内,空心弹内部流动是超音速流动,斜激波在弹丸内壁面反射形成一系列与入射激波相似的反射激波,最后一直延伸到尾部,与弹底膨胀波系相互干扰,弹底压力急剧减小。激波在弹丸内部交汇从而产生高压区,随着马赫数的降低,斜激波在弹内的交汇点提前了,在弹内壁的反射次数随之增加。在马赫数为4.0时,激波在空心弹内壁上的第三次反射落在弹丸内壁尾部;在马赫数为2.0时,激波在空心弹内壁上形成8次反射。
2) 马赫数在2.0以下时,如图8~图11所示,弹丸头部不再形成附体斜激波,转而产生脱体激波,超音速来流经过脱体激波后,气体将以亚音速流动,弹丸内部发生阻塞,无法形成超音速流动,阻力突然增大。因此,必须消除脱体激波才能减小弹丸所受波阻。
根据仿真结果,弹丸的临界阻塞速度约为612 m/s(1.8 Ma),而按文献[12]给出的空心弹发生“阻塞”的计算公式计算得弹丸的临界阻塞速度为625.6 m/s(1.84 Ma),仿真所得阻塞速度与公式计算所得阻塞速度基本一致。
3.2仿真所得阻力系数与文献[13]所给出的计算公式计算结果对比
表2列出了不同马赫数条件下仿真与文献[13]所给出的计算公式所得阻力系数。
由表2可见,来流马赫数为1.2~4.6时,两种方法所得摩擦阻力系数相对误差均在15%以内;来流马赫数为2.0~4.2时,压阻系数相对误差也在15%以内;来流马赫数Ma在2.0~4.4时间时,总阻力系数的相对误差小于10%。
为研究空心弹头部前缘厚度的微小变化以及弹带对其阻力系数的影响,将模型2~模型8仿真所得阻力系数与表2中的按文献[13]所给出的公式计算结果进行对比,计算其相对误差,如表3所列。
由表3可看出,来流马赫数为2.0~4.4时,模型2、模型3、模型4总阻力系数的相对误差小于10%,弹丸头部前缘厚度对阻力系数影响较小;来流马赫数小于4.0时,模型5、模型6、模型7总阻力系数的相对误差大于10%,弹带对阻力系数的影响较大。
3.3外弹道计算结果与分析
以2.2节空心弹模型1为算例1,以模型8为算例2,以与模型1相似的另一种混合锥形空心弹为算例3。算例3的具体结构参数为:D0=105 mm,Di=98.6 mm,Dt=82.6 mm,L=254 mm,θ0=3°,θi=3.5°。
取弹丸初速为1 292 m/s(3.8 Ma),另按平均体积和材料密度得出质量数据。采用Matlab软件分别对仿真所得阻力系数结果与文献[13]所给出的公式计算结果进行拟合,并建立空心弹质心运动微分方程组。经仿真解算,得到0.5°、1°和2°三种射角下分别用仿真所得阻力系数拟合曲线函数表达式(方法A)和用公式计算所得阻力系数拟合曲线函数表达式(方法B)数值解算空气质点外弹道得到的顶点诸元和落点诸元和如表3和表4所列。
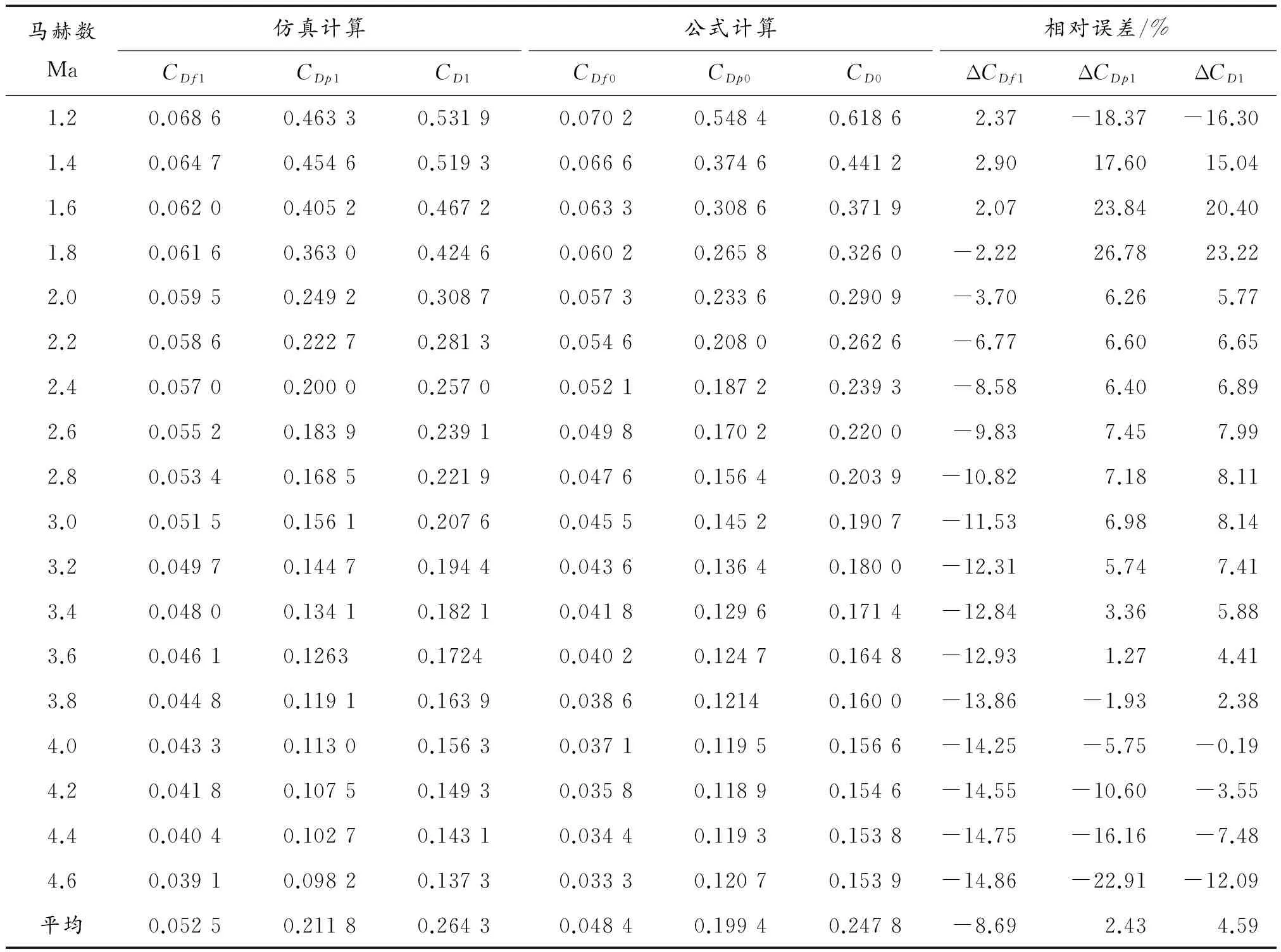
表2 不同马赫数条件下模型1仿真与公式计算所得阻力系数

表3 模型2~模型8仿真结果与公式计算结果相对误差(%)
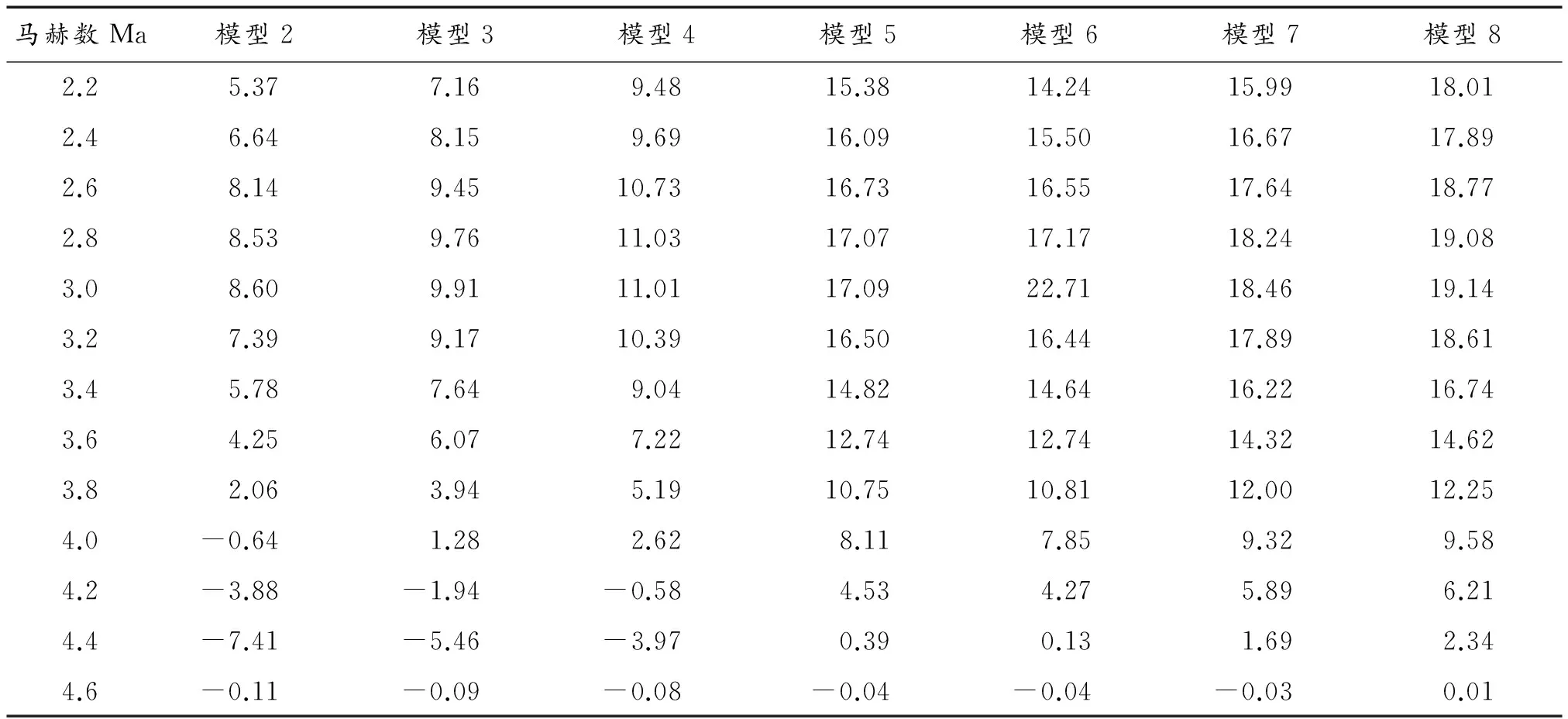
续表(表2)

表3 不同射角下用方法A和方法B数值解算的外弹道顶点诸元

表4 不同射角下用方法A和方法B数值解算的外弹道落点诸元
从表3和表4可以看出,算例1和算例3应用两种阻力系数解算外弹道所得的外弹道顶点诸元和弹道落点诸元相对误差很小,在3.35%以内;算例2所得外弹道顶点诸元相对误差在6.69%以内,落点诸元相对误差在10%以内。
对于图1所示的空心弹结构,在特定速度范围内,用上述两种方法得到的阻力系数解算外弹道所得顶点诸元与落点诸元相差很小。但在工程设计时,空心弹结构不可能与图1所示的空心弹简化结构完全相同。增设弹带后,仿真所得阻力系数与文献[13]所给出的公式计算所得阻力系数差别较大,用两种阻力系数解算外弹道所得顶点诸元与落点诸元相差也较大,因此未考虑弹带部分影响的空心弹简化模型阻力系数文献[13]所给出的计算公式不太适合于工程问题。
4结论
本文应用Fluent软件对空心弹流场进行数值模拟,分析了不同马赫数下空心弹的流场特性,将数值仿真得到的空气动力参数与用文献[13]所给出的公式计算所得的“理想情况下的”空气动力参数对比,并分析其差异,对比了应用数值仿真所得阻力系数计算的质点空气外弹道诸元与应用公式计算所得阻力系数计算的诸元。结果表明:
1) 在来流马赫数为2.0~4.4的条件下,针对无弹带结构的简化的空心弹模型数值模拟所得阻力系数结果与用文献[13]所给出的公式计算所得阻力系数基本一致,用这两种阻力系数分别计算空心弹空气质点外弹道所得顶点诸元和落点诸元相差很小;
2) 空心弹的工程设计与上述简化的理论模型不可能完全相同,主要差别在弹丸头部前缘厚度和弹带结构。其中弹丸头部前缘厚度在可信区间内对阻力系数影响较小,但弹带结构对阻力系数的影响较大。增设弹带后,用两种方法得到的阻力系数解算质心空气外弹道所得顶点诸元与落点诸元相差较大,即理想情况下推导出的空心弹简化模型阻力系数文献[13]所给出的计算公式不太适合于工程问题求解,此时应以数值仿真为主。
参考文献:
[1]王雨时.西方国家的空心弹技术[J].弹箭技术,1996,9(3):1-10.
[2]王雨时.西方国家的空心弹技术(续)[J].弹箭技术,1996,9(4):14-22.
[3]周立宪.管式弹丸阻力特性研究[D].南京:南京理工大学,2004.
[4]高旭东,钱建平,王晓鸣,等.基于流场数值模拟的空心弹阻力特性优化方法[J].弹箭与制导学报,2004,24(4):161-162.
[5]高旭东,钱建平,王晓鸣,等.空心弹流场数值模拟与阻力特性[J].南京理工大学学报,2005,29(2):158-161.
[6]任登凤,谭俊杰,张军,等.非结构隐式方法在空心弹流场模拟中的应用[J].力学与实践,2006,10(5):24-27.
[7]钱吉胜,李艳玲,陈志华,等.低阻空心弹流场特性研究[J].弹箭与制导学报,2011,31(4),73-75.
[8]李艳玲,陈志华.口径30mm空心弹真实条件下的气动特性研究[J].航空计算技术,2011,41(5):76-80.
[9]李艳玲.低阻空心弹的数值设计研究[D].南京:南京理工大学,2012.
[10]黄振贵,李艳玲,陈志华,等.空心弹的阻力特性与气动外形数值分析[J].兵工学报,2013,34(5):535-540.
[11]WU J J,SARGENT E R,ROBRET B.High Performance Hollow Projectiles.AD 0768907[R].California:U.S.Department of Commerce National Information Service,1973.
[12]李惠昌,杨金耀,祁荣长.空心弹丸的研究[J].兵工学报,1980,2,32-41.
[13]LAVIOLETT MAURICE A.Tubular Projectile:US,4164904[P].1979-08-21.
[14]LAVIOLETT MAURICE A.Short Range Tubular Projectile:US,4827847[P].1987-02-21.
(责任编辑周江川)
收稿日期:2016-01-25;修回日期:2016-02-20
作者简介:张浩(1992—),男,硕士研究生,主要从事引信、弹药技术研究。 通讯作者:王雨时(1962—),男,教授,本刊编委,主要从事引战系统分析与设计研究。
doi:10.11809/scbgxb2016.07.002
中图分类号:TJ011.2
文献标识码:A
文章编号:2096-2304(2016)07-0005-07
Theoretical Calculations and Numerical Simulation on Air Resistance Characteristics of Hollow Projectile
ZHANG Hao,WEN Quan,WANG Yu-shi,ZHANG Zhi-biao
(School of Mechanical Engineering, Nanjing University of Science & Technology, Nanjing 210094, China)
Abstract:Simplified model hollow projectiles with typical design scheme was numerically simulated by Fluent software. The relationship between drag coefficient and Mach number was got. On this basis, trajectory centroid group equations of motion were solved using Matlab software, and the firing data of trajectory vertex and impact point was obtained. Compared the simulation results of drag coefficient above and ballistic firing data with theoretical formula calculation results, its shows that the results of simplified model hollow projectiles between simulation and theoretical calculations has a little difference when incoming flow Mach number between 2.0 and 4.4. Leading edge thickness of hollow projectile has little effect on the drag coefficient in the confidence interval, but rotating band structure has a greater impact on the drag coefficient. Be effected by rotating band structure, the drag coefficient theoretical formula of simplified model hollow projectile is not suitable for solving engineering problem. Engineering design should be based numerical simulation.
Key words:hollow projectile; simulation; theoretical formula; drag coefficient; exterior trajectory
【装备理论与装备技术】
