基于决策者风险偏好的直觉语言数排序方法

2016-08-09王中兴刘久兵

信阳师范学院学报(自然科学版) 2016年1期

王中兴，陈晶，刘久兵

(广西大学数学与信息科学学院，广西南宁 530004)

0 引言

直觉模糊集作为模糊集的重要扩展，其同时考虑隶属与非隶属度两方面信息，更加细腻地刻画事物“非此非彼”的模糊本质.自1986年Atanassov[1]提出直觉模糊集的概念以来，直觉模糊集的理论发展迅速，并在决策领域得到了广泛的应用.文献[2]对直觉模糊信息集成方法进行研究，提出了直觉模糊数加权几何(IFWG)算子、有序加权几何(IFOWG)算子和混合几何(IFHG)算子，并应用到多属性决策中.文献[3]进一步拓展直觉模糊集，提出了区间直觉模糊集的概念，用区间数来表示直觉模糊集中的隶属度和非隶属度，并定义区间直觉模糊集的一些基本运算.文献[4]继续深入拓展直觉模糊集，用三角模糊数表示隶属度和非隶属度，提出了模糊数直觉模糊集的概念，同时给出了模糊数直觉模糊集的一些运算.文献[5-6]在直觉模糊集和语言评价集的基础上定义直觉语言数、直觉二元语义及其相关概念.文献[7-8]推广直觉语言数到直觉不确定语言数，并提出直觉不确定语言数运算法则、序值关系及直觉不确定语言数集结算子.

在研究基于直觉语言数表示属性值的模糊多属性决策方法时，一般都需要对直觉语言数进行比较与排序.文献[5-6,9-10]考虑直觉语言数的犹豫度对其得分函数的影响，提出了融隶属度、非隶属度和犹豫度为一体的得分函数并联合精确函数对直觉语言数进行择优与排序.然而上述文献都侧重从客观角度设计得分函数，忽视了决策者的风险偏好对决策的影响，而在不确定环境下，决策者的风险偏好往往直接影响到决策结果.本文根据直觉语言多属性决策的特征，综合直觉语言数的得分函数与决策者的风险偏好，提出直觉语言数的风险得分函数，并以此作为直觉语言数排序指标.

1 预备知识

定义1[11-12]设语言评价集S={s-τ,s1-τ,…,sτ}是一个非空集合.语言术语si是事先定义的评价短语(如“好”、“一般”、“差”等).例如，五粒度语言评价集可以表示成S={s-2,s-1,s0,s1,s2}={很差,差,一般,好,很好}.语言评价集S满足一般性质：

1)有序性：若i≥j时，则sisj.

2)取大(max)取小(min)算子：当sisj时，则

max{si,sj}=si,min{si,sj}=sj.

3)存在逆否(neg)算子：neg(si)=s-i.

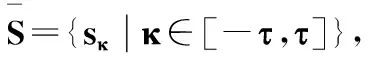
H={〈sη(x),uH(x),vH(x)〉x∈X},∀x∈X,πH(x)=1-uH(x)-vH(x)表示决策者的犹豫度.

u(β)-u(α)u(β),v(α)v(β)〉，

neg〈sη(α),u(α),v(α)〉=〈s-η(α),u(α),v(α)〉.

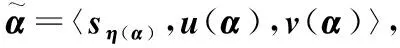
(1)

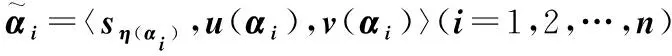
(2)

2 直觉语言数排序方法

2.1 直觉语言数的得分函数与精确函数

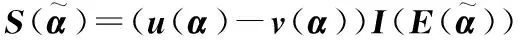
和精确函数

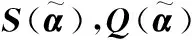
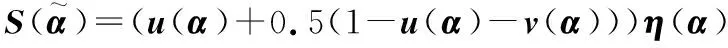
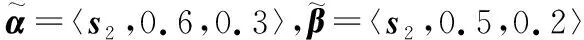
2.2 基于决策者风险偏好的直觉语言数排序方法

基于上述不同偏好的决策者对直觉语言数的犹豫度对其影响的不同，本文提出含决策者的风险偏好的直觉语言数排序新方法.

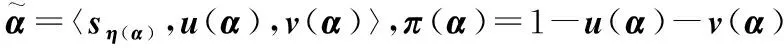
其中λ∈[0,1]表达决策者的风险偏好.如果1≥λ>0.5，则认为决策者是追求风险(冒险)的；如果0≤λ<0.5，认为决策者是畏惧风险(规避风险)的；如果λ=0.5，认为决策者是风险中立的.

下面通过例子将本文排序指标与现有的一些直觉语言数的排序指标所得排序结果进行比较分析(如表1).

表1 不同排序指标的排序结果比较

以上对比分析表明，本文排序指标融入了决策者的风险偏好，在对直觉语言数进行排序时，其排序结果更符合实际情形．

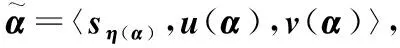
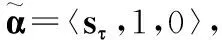
(充分性) 由风险得分函数的定义有

(1-λ)π(α))(u(α)+λπ(α))η(α).

(3)

因为∀λ∈[0,1]，都有

0≤u(α)+λπ(α)≤

u(α)+π(α)=1-v(α)≤1,

(4)

0≤v(α)+(1-λ)π(α)≤

v(α)+π(α)=1-u(α)≤1,

(5)

所以

-1≤u(α)+λ(1-u(α)-v(α))-v(α)-

(1-λ)(1-u(α)-v(α))≤1.

(6)

u(α)+λπ(α)-v(α)-(1-λ)π(α)=1，

(7)

u(α)+λπ(α)=1，

(8)

η(α)=τ.

(9)

2) 同理可证.

3 基于含风险偏好评分函数的直觉语言多属性决策方法

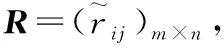
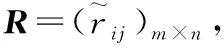
neg〈sη(α),u(α),v(α)〉=〈s-η(α),u(α),v(α)〉.

步骤3 利用定义5的ILWAA算子对方案Ai的直觉语言信息进行集结，得到Ai的综合直觉语言评价值zi(i=1,2,…,m).

步骤4 根据定义7计算各方案的风险得分函数Sλ(zi)(i=1,2,…,m)的值.

步骤5 根据Sλ(zi)(i=1,2,…,m)值，按定义8对各方案择优与排序.

4 实例分析

某风险投资公司进行项目投资，采用4个评价属性{G1,G2,G3,G4}={风险因素,成长因素,政治因素,环境因素}，对4个备选企业{A1,A2,A3,A4}，选用九标度语言评价集S2={s-4,s-3,s-2,s-1,s0,s1,s2,s3,s4}={极差,很差,较差,差,一般,好,较好,很好,极好}，进行评价.其中属性权重向量为w=(0.30,0.25,0.20,0.25)T.该公司综合考虑公司的利益和市场的需求，给出每个备选企业在各个属性下的评价值，如表2和表3.