基于正则化的模糊C-均值聚类算法及其在T-S模糊系统辨识问题中的应用

王 艳, 徐再花, 张大庆

(辽宁科技大学 理学院, 辽宁 鞍山 114051)

0 引言

结构辨识是模糊系统辨识的重要任务.通过它,首先确定被辨识系统的输入和输出变量,然后完成模糊子空间的划分任务,并最终确定待建立的模糊模型的规则数.

模糊聚类算法在划分模糊系统输入空间时取得了较好的效果.但由于对初始值敏感,并且在寻找聚类中心时存在迭代过程,因此计算量大,而且容易出现局部极小和中心冗余等问题.为了解决这些问题,出现了许多改进的模糊聚类算法,如Chen[1]提出了一种增强FCM(Fuzzy C-mean)算法,成功地实现了复杂系统的模糊建模;Alexiew等[2]提出使用Hough变换确定聚类数和初始数据划分来避免陷入局部极小;Tsekouras等人[3]提出一种递阶模糊聚类建模方法,采用最近邻聚类初始聚类中心,通过加权FCM聚类优化聚类参数的方法建立模型.

然而本质上,FCM聚类算法是一个反问题.它由数据出发来重建模型.反问题在一定的条件下,会存在不适定性[4-5].但已有文献中,还没有见到在设计FCM算法时,考虑到不适定性给算法带来的影响.目前解决不适定性问题较有效的方法是正则化方法[4-5],它对数据的微小扰动引起解的严重失真有很好的改善作用,使算法抗干扰能力增强.

本文的主要贡献是在FCM聚类算法中引入正则化方法,通过在目标函数中添加正则化泛函,构造出新的模糊聚类算法—RBFCM(Regularization based Fuzzy C-means)算法,由此增强了模糊聚类算法针对数据扰动的鲁棒性.进一步,将此RBFCM算法应用到基于T-S模糊模型的系统辨识问题中,得到了基于正则化方法的T-S模糊系统辨识方法,从而改善模型的适定性,又使模型的前件输入空间得到优化,进而使模型的结构得到优化.通过对IRIS数据集以及带有噪声的IRIS数据集的聚类算例,验证了RBFCM算法不仅具有较高的聚类精度,且具有很好的抗干扰能力.针对Box-Jenkins煤气炉数据集的辨识算例结果表明,基于RBFCM算法的T-S模糊系统辨识方法,不但具有较高的辨识精度,且由对比知,在相同的初始条件下,可以较少的规则数达到理想的辨识精度,并相对减少了迭代的步数.

1 基于正则化的FCM算法

1.1 FCM算法

考虑一个样本集合

X={X1,X2,…,XN},

其中Xk=[xk1,xk2,…，xkn](k=1,2,…,N),N为样本数.分样本集合为c类,c∈{2,3,…,N-1},记vi为第i类的中心,令V=(v1,v2,…,vc)为聚类中心矩阵.每一类可以用它的聚类中心vi来代表.

FCM算法试图找到最能代表每一类特征的点,即可以作为这一类的中心的点以及每个数据点在各类中的隶属度.这个目标可以通过最小化目标函数来实现.一个常用的目标函数定义如下：

(1)

其中,m∈(1,)是一个权重指数,通常取m=2.记U=[uik]为隶属的矩阵,满足下列条件:

(2)

FCM聚类算法在迭代过程中优化分类.每个迭代过程中改善参数U和V,直到它到达稳定终止条件.

1.2 RBFCM算法

常用的正则化方法包括Tikhonov正则化方法与谱截断法.在这里,应用前者来改善FCM算法的适定性.后者多见于线性不适定问题.定义新的目标函数：

(3)

其中,α是正则化参数,控制着

和

类似于标准FCM的参数求解方法,综合条件(2),应用拉格朗日乘积因子法来求解目标函数(3)的最优值.令

(4)

首先计算L(U,V,λ)关于Uik和λk,(i=1,2,…,c,k=1,2,…,N)的偏导数并令它们等于零,有

(5)

(6)

由式(5)可得:

(7)

将式(7)代入式(6)得

(8)

再将式(8)代入式(7)得计算隶属度的迭代公式:

(9)

之后计算L(U,V,λ)关于vi(i=1,2,…,c)的偏导数并令其等于零,可得

(10)

于是有

(11)

式(9)与式(11)给出了隶属度uik和聚类中心vi的隐式计算公式,需要构造迭代算法进一步求解.

RBFCM算法:

Step1.初始化.给出聚类数c,选取权重系数m=2,正则化参数α=1,给定容许误差ε和迭代步数l=0;

Step2.用减法聚类获取FCM算法的初始聚类中心,即

(12)

Step3.通过下式计算隶属度:

(13)

Step4.用下式修正聚类中心:

(14)

以及通过岭迹法[6]修正参数α(l).

Step5.若‖U(l+1)-U(l)‖<ε,则停止算法,输出模糊划分矩阵U和聚类中心V;否则令l=l+1;重复步骤Step3至Step5直到收敛.

2 基于算法RBFCM的T-S模糊系统辨识

T-S模糊模型可以用如下的If-Then模糊规则描述[7]:

Ri: Ifxk1isAi1and…andxknisAinThen

(15)

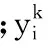
对模糊集Aij采用高斯类隶属函数

(16)

其中,vij为输入变量的聚类中心值,σij为高斯类隶属函数的宽度,σij的计算公式如下:

当R=c时,T-S模糊系统辨识得到的第k个输入对应的输出为每个规则输出的加权平均：

(17)

这里,

πi=[pi0,pi1,…,pin]T,(i=1,2,…,c)

为第i条规则的结论参数,其中

X(k)′=[λ1k,…,λck,λ1kxk1,…,λckxk1,…,

λ1kxkn,…,λckxkn],(k=1,2,…,N);

P=[p10,…,pc0,p11,…,pc1,p1n,…,pcn]T.

当给定一组输入输出数据

[xk1,xk2,…,xkn]→yk(k=1,…,N)

时,可令Y=XP,其中,Y=[y1,…,yN]T,矩阵X由下面的式(18)确定.

X=X0,X1,…,Xn,

(18)

i=1,2,…,n.由此,可得结论参数的计算公式为：

P=(XTX)-1XTY.

(19)

当前件变量已经选定,而且模糊子空间划分的个数已确定,确定模糊子空间的问题就是确定前件中的隶属函数,也即是确定使性能指标达到极小的隶属函数中的参数.下面将应用算法RBFCM聚类算法和最小二乘法求解T-S模糊系统的辨识问题.

基于RBFCM的T-S模糊系统辨识:

Step1.确定输入空间分类数c.

Step2.运用算法RBFCM计算隶属度矩阵U=[uik]和聚类中心V=(v1,v2,…,vc);

Step3.构建T-S模糊模型,用式(16)辨识出模型的前件参数;利用最小二乘法求解式(19)辨识出后件参数;

Step4.利用加权式(17)可计算出模糊模型的输出.通过下式计算模型误差.

3 仿真示例

例1 考虑IRIS数据集.IRIS数据集的实际类中心VT为：

V1=(5.006,3.428,1.462,0.246),

V2=(5.936,2.77,4.26,1.326),

V3=(6.588,2.974,5.552,2.026).

各聚类中心到实际类中心的距离用下式计算：

IRIS数据集的聚类结果如表1所示.可以看出,算法RBFCM有更快的收敛速度.由于添加了稳定泛函,使算法具有更好的稳定性,所得聚类中心与标准FCM算法的聚类结果比起来更加逼近于实际的聚类中心.同时最终得到的第2和第3类样本的聚类中心也较为分开.

为了验证算法的抗噪能力,在IRIS数据集的每一数据点上加一个服从[0,0.1]区间上均匀分布的随机噪声ε.带有噪声干扰的IRIS数据集的聚类结果如表2所示.从表2中可以看出标准FCM算法由于干扰数据集的存在,得到的聚类中心越来越远离实际聚类中心,而算法RBFCM由于添加了稳定泛函,使所求聚类中心稳定在真实聚类中心的一个较小的邻域内,起到了稳定所求解的作用,因此使改进后的新算法在抗干扰能力方面得到一定的提高,并兼顾了逼近性和稳定性的要求.

表1 三个算法在IRIS数据集上的分类结果比较

表2 三个算法在带有干扰的IRIS数据集上的分类结果比较

例2 考虑Box-Jenkins煤气炉数据集[8].文献[9]对这一实例比较了许多研究者的结果.表3给出了采用基于RBFCM的T-S模糊系统辨识方法在聚类个数均为2的情况下对不同前提变量的模糊规则进行系统辨识的建模效果,并且比较了在不同建模方法下的均方根误差.从表3中可以看到基于RBFCM的T-S模糊系统辨识方法所建立的模糊系统规则数最少仅为2,但辨识误差相对较小.因此该方法可以以较少的规则数达到较高的辨识精度.在输入变量个数同为3时,Sugeno93模型在规则数为6时精度达到0.435,相比之下基于RBFCM的T-S模糊系统辨识方法在规则数为2时精度即可达到0.365 6,也说明了该方法在辨识精度方面有所改善;在模型输入变量个数6与规则数2均相同的前提下,显然有0.247 9<0.261 0.从比较结果可以看出，RBFCM算法使所得到的T-S模糊模型,不但具有较高的辨识精度,而且在相同的前提变量条件下,可以以较少的规则数达到理想的辨识精度.这是因为RBFCM算法中的正则化泛函即可改善前件参数计算过程的适定性,又使模型的前件输入空间得到优化,模型的结构得到优化，从而使基于RBFCM的T-S模糊系统辨识方法兼顾了稳定性和逼近性的要求.

表3 Box-Jenkins煤气炉数据辨识误差比较

4 结论

结合正则化方法、减法聚类算法对标准FCM聚类算法进行了改进,提出了基于正则化方法的模糊聚类算法-RBFCM算法.之后将RBFCM算法用于基于T-S模糊模型的系统辨识问题中,优化了输入空间的划分,从而优化了模型的结构.仿真示例表明,RBFCM算法不但具有较高的聚类精度,且具有一定的抗干扰能力.基于RBFCM的T-S模糊系统辨识方法不但能提高建模精度,而且由对比结果知,在相同的初始条件下,可以以较少的规则数达到理想的辨识精度.