粒子物理中几种可能应用的新数学方法和拓扑模型

张一方

(云南大学 物理系，云南 昆明 650091)

0 引言

众所周知，量子力学和粒子物理的发展应用了一些和以前的理论不同的数学工具，如算符、矩阵表示、Hilbert空间等.并发展出某些新的数学结果，最著名的有量子力学的新方程、Bose-Einstein(BE)和Fermi-Dirac(FD)统计、Yang-Mills规范场等[1-5].统计原理是量子力学和整个物理学的基本原理， 1986年9月Dirac在论述《原子物理的未来》时认为对以前研究不够的不完全可约表示，或称为病态表示可能在物理学中有重要应用.20世纪80年代Connes非对易微分几何可以把Higgs场解释为离散点空间上的规范场，相应的Higgs势成为它的Yang-Mills作用.这对应非线性.Coquereaux等和Sitarz分别应用矩阵运算和离散群上的微分运算等方法阐述Connes的离散空间上非对易几何的基本思想.笔者讨论了非平衡统计和统计的某些应用，然后研究各种统计方程及其与量子理论的关系，探讨高能时的统计性及此时具有的新特征[6].本文探讨了四元数、符号动力学等几种新的可能应用于粒子物理中的数学方法，并且具体研究了粒子的拓扑模型和弱相互作用可能相应于Lobachevsky几何.

1 粒子物理中几种新数学工具的探讨

实数域中无零因子的有限维的交错代数仅有四种：1)实数域,是交换代数；2)复数域,是交换代数；3)四元数代数，是非交换代数；4)Cayley代数是非结合交错代数.它们的维数分别是1、2、4、8.四元数代数和Cayley代数可以是非交换的，特例即反交换.其中四元数代数的后三个元素，Cayley代数的后七个元素都是两两反交换的.它们有可能统一玻色子和费米子.这又对应于超对称.

Grassmann数对应费米子和超弦.其联系于四元数对应虚数和实数.结合相对论，三个实数对应光子、W、Z或三个胶子，三个虚数对应三个轻子或三个夸克.

按杨振宁四元数的想法，l、i、j、k分别相应于光子γ(或W)、π介子、中微子v和质子p或γ、引力子g、v和p，由此包括全部粒子.以后发展为八个元素l、i、j、k，e、ie、je、ke，相应于γ、W、πg，v、e、p、n(u,d)或γ、W±、Z0，v、e、νμ,μ或八个胶子之半，或u、d、c、s，或第一代夸克-轻子和γ、W、g0、g+等.或者八元数相应于八个亚夸克.或四元素相应于强子，甚至仅相应于SU(3)，相应于引力子g和三个夸克u、d、s.

布鲁塞尔振子(Brusselator)和Lotka-Volterra(LV)模型都产生振荡，都是非线性方程组，对应周期性及非线性的回归性[9-10].二者都有极限环，结合笔者以前提出的粒子相互作用和相变理论[11]，可以用于量子理论和粒子物理.

不稳定振荡对应布鲁塞尔振子.这必须相关的双因素，如强、弱相互作用.布鲁塞尔振子修改后就可以联系于相互作用的量子场方程组，如动力学模型中的各种方程组，或自相互作用方程.由此联系于粒子的极限环.而方程组结合孤子方法可以化为常微分方程.

它们都是非Abel群，应结合场论和非平衡统计.此时非平衡系统可以分为近线性(如能量渐变)和远离平衡的非线性(碰撞).其一，因为ep碰撞是电磁相互作用，所以，1)如果仅考虑强相互作用，则这只是对核子输入能量，其达到一定阈值时就产生有序结构——部分子.这种产生应有能阈，高能电子为4.5～20 GeV.并且各种碰撞如忽略相互作用都是输入能量.2)ep的电磁方程一般不是非线性方程.其二，核是强相互作用，略去电磁相互作用则np对称.核子方程非相对论时是有势的Schrodinger方程.其三，中微子v振荡是弱相互作用.

2 非线性理论和定性分析的结果

笔者讨论过粒子物理中的各种非线性理论，如非线性波、非线性方程、复时空及其与几何、数学等的关系和可能的检验[12-13].并且由此可以研究各种可能的Pauli不相容原理的破缺和相应的统一，及与量子场论、任意子、分数统计、反常现象、自旋和碰撞等的关系[14-15].一般而论，分岔-混沌对应相变，极限环对应强子.由砂子形成粒子，对应宇宙早期的强子-轻子时代.这些都可以用定性分析理论，得稳定或不稳定的粒子.并由粒子质量确定某些不等式.强相互作用对应汇，弱相互作用对应源，二者及电磁相互作用共同作用对应鞍点、极限环等.

在动力学模型中，令x～ψ，y～φ，z～Aμ，对动力学破缺方程组为[7-8]：

x′=-Axz-meayx,

(1)

y″=μz′+Beayx2,

(2)

z″=-Czz′-μ2z-μy′+Dx2.

(3)

对Higgs破缺方程组为[7-8]：

x′=-Axz-mx+ay2x,

(4)

(5)

(6)

对方程(5)和方程(6)，常数适当时化为：

y′=c-(bx2-dz2)y+f2y2,

(7)

(8)

3个方程两两组合则形成各种情况.其中可以假设x是重子、轻子；y是介子；z是相互作用场，光子等.

1)Aμ=0，则

x′=-mx+axy2，

y′=c-bx2y+fy2.

(9)

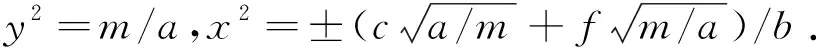
(10)

特征方程为：

λ2-Tλ+D=0,

(11)

其中:T=-m+2fy+ay2-bx2，D=mbx2+3abx2y2+2afy3-2mfy.c=0，则可以简化.对(0,0)(对应真空态)，T=-m<0，D=0.

2)φ=0，则

x′=-mx-Axz，

z′=-Cz2-μz+ex.

(12)

对x′=0，z′=0，得x=0,z=0；或z=-m/A，x=(m/eA)((Cm/A)-μ).特征行列式为：

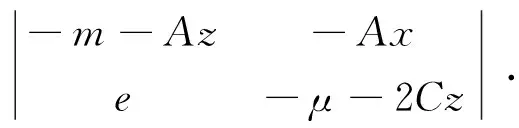
(13)

特征方程中:T=-(m+μ)-(A+2C)z，D=mμ+Aex+(Aμ+2Cm)z+2ACz2.对真空态(0,0)，T=-(m+μ)<0，D=mμ>0是汇.Δ=(m-μ)2≥0是结点.其余可以确定x1,z1点.

结合已知数学还可以推知粒子种类和数目、量子数等.四相(五奇点)可用于每代轻子-夸克四种(v,e,u,d)，两轴各是轻子-重子量子数等.进一步，结合动力学模型，二、三代有8,12种.其中三代可以为三层中心点等.

笔者应用非线性方程的定性分析理论研究了双星演化模型[16-18]和地震预报[19-20]等.结合协同学，对非线性系统可以用役使原理等.进一步，可以把耗散结构理论、突变论、超循环论和自组织等应用于粒子物理中.

3 粒子的拓扑模型和分形

杨振宁认为粒子物理的数学发展方向是几何与拓扑.Weinberg在他的名著《The Quantum Theory of Fields》中已经用了拓扑学，并讨论了拓扑分类、拓扑守恒定律和拓扑不变性等[21].在此具体讨论粒子的拓扑模型.

量子场论中，Feynman图在若干方面已经类似拓扑结构、拓扑模型.它可以结合点-连杆模型，这就是顶点-线.但是拓扑模型是线相同而点不同，这是点相同而线不同，表示一种相互作用，对应连接方法.Feynman图中与能量E无关，对应拓扑无关性.如此只要初末态粒子确定，则不论E如何，碰撞骨架都相同，即只与截面S、初末态粒子相关.

基于图论中树-域和Feynman图的结合，笔者提出图论的一种新发展，其中包括5种基本元素：实线、点线、波形曲线、顶点和域，并且讨论了其在物理、生物等领域中的可能应用[22].粒子起码可以用拓扑方法描述.这联系于夸克-靴带二重性.拓扑模型结合粒子，可能量子数就是拓扑指数.拓扑不变性相应于粒子的守恒量和变化的不变性.可以设想亏格不同就是量子数B、S、I不同.基态重子N、Λ、Δ、Σ、Ξ、Ω相应于规范曲面，可能对应于费米子.玻色子可能对应于曲线.共振态仅是同胚变型.光子相当于Mobius带，Klein曲面.量子数B、S、I是三个自由度，对应于重子及两个同心球中间的部分.B=0时是二个自由度，对应于介子及环面.对基本粒子，这是分离的.

目前粒子不同是夸克不同，此时就是拓扑结构不同，特别是不同代.类似动力学模型，在振动-转动模型中就是运动不同[7].但目前拓扑模型等的困难以及整个理论的困难在于强子甚至质子p由几个亚粒子组成都不确定.

对拓扑粒子理论，拓扑的某个特征，如维数等就是最关键的数，拓扑荷、量子数对应于粒子数或量子数，如B、I或S等.这就联系于拓扑熵、Feynman图等.在粒子的拓扑模型中同胚、连通阶可能对应于费米子数或量子数S,I等.由此可能又联系于弦，对应于粘贴和截开，二者又对应于拓扑学中的相互作用和衰变.而且可以探讨与强相互作用、夸克的组合等的关系.

场论中的粒子可以用具有拓扑奇性的矢量场描述.无相互作用对应拓扑线平行，相应于熵增；有相互作用对应拓扑线有奇点，相应于更一般的统计力学.标度不变性可以结合拓扑不变性.可以由拓扑导致矢量场，并得到纤维丛和规范场.

拓扑学上粒子、袋都可以化为点，但闭弦就等价于环.粒子对应弦、袋都是同胚的.弦实际是，而且应该发展为管和膜模型，这可能又联系于高维弦.

稳定重子由三个夸克组成只能是等边三角形结构，对应分形模型[7,23]中的分维D为

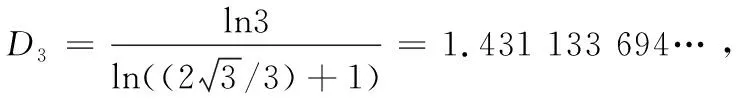
(14)

在空间中是各种立体，如三夸克-三胶子在空间中以稳定的正八面体形式组成，则相应分形模型的分维为

(15)

或五夸克-胶子组成类似结构.否则不稳定或亚粒子更多.

粒子的分形由相关函数、分布函数得D，统计分形应该可以发展，特别结合分形模型.由宇宙弦可以导出分维D，则量子弦也应可以导出分维.

如果夸克是一种字母空间，即紧致拓扑空间.夸克数就是字母个数为n，相应的拓扑熵为logn>0，ln3(2)=1.099(0.632)，ln4(6)=1.386(1.792).而有限字母组成的符号空间中的移位自同构具有混沌的很多性质.各种粒子，如核子、原子、分子，乃至人、天体的结构都可以认为与此相似.更一般，低维与高维的物理方法是相似的.这些都可能与物理反常、数学拓扑有关.

4 弱相互作用可能相应于Lobachevsky几何

目前公认的相互作用有四种：引力、弱、电磁、强相互作用.对此首先必须严格区分、定义各种相互作用，特别是粒子物理中特有的短程的强、弱相互作用.而目前的主要依据都存在一些问题，例如根据相互作用强度，但如此不可能有衰变，因为弱相互作用不能克制强相互作用.根据相互作用距离，则如何确定临界值？而且通常认为距离短时是强相互作用，再短时是弱相互作用，但粒子内部是渐进自由，夸克之间又是胶子作用.笔者已经讨论过粒子物理中存在短程的强、弱相互作用与作用距离的矛盾.根据相互作用时间，对强相互作用的粒子稳定.根据粒子种类，则A→Bπ都是强子，但是弱衰变.强、电磁、弱相互作用都有寿命(宽度)、衰变、散射等.而且强弱相互作用都对应SU(3)对称性及其破缺.

4.1 弱相互作用的基本特性

斥力导致变速运动，这是相同的，但方向相反，这又不同，在等价原理中旋转系方向相反.非欧几何中，曲线坐标的数学是相同的，都有协变、逆变矢量.度规张量都是一般的.弱相互作用可能对应Lobachevsky几何.进而笔者提出几何、力和相互作用的对应关系(表1).由此研究Lobachevsky几何得到的场方程，及与Riemann几何的结果的异同.它是Riemann几何中的三角函数换成双曲函数[24].这对应于开空间.彼此跑开，相应红移.对弱相互作用，这相应于某些新的效应.

表1 几何、力和相互作用的对应关系

广义相对论对应于度规，是一般的非欧几何.这应该对应于泛广义相对论[25-26].而弱的引力相互作用是Friedmann空间.此时决定于空间曲率k，对应于临界密度、临界值.推广后可以由k<0的弱荷定义弱相互作用.这样则强弱相互作用决定于k.它是广义相对论结合微观相互作用的结果.

由弱相互作用到强相互作用必然有一个相变点，类似两种几何之间的关系.二维时就是：

(16)

其中:e<1是椭圆；e>1是双曲线；e=1是抛物线.这应该可以推广到3、n维空间.

目前规范理论中弱强相互作用分别相应SU(2)和SU(3)对称群，而没有反映它们的这个关键性的不同.对于负物质[21-31]，强弱相互作用仍然分别是引力和斥力，或者相反.

4.2 SU(2)弱相互作用理论

对应标准规范场.在对应原理下，化为弱相互作用场方程，应该包含SU(2)方程，对应内山场得到SU(2)规范场.进而应该研究短程线方程是否相同，也可能形式相同，而Γ符号相反，这如何导致、联系于斥力，不同在于对应的是规范场，运动方程是

(17)

场方程是

γμ(∂μ-iετbμ)ψ+mψ=0.

(18)

弱场及SU(2)中粒子如何运动？其中三角函数如何？Lobachevsky几何中仍是短程线.首先必须使量子场方程Aμ，ψ与广义相对论、非欧几何的运动方程、场方程对应起来.而曲率张量对非欧几何是普适的.应该由

(19)

导致上述运动方程.

对Yang-Mills(YM)规范场

(20)

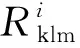
弱相互作用、SU(2)规范场、Lobachevsky几何三方面的特性应该彼此结合.而后两方面互相联系.

完备的理论结果应该包括：1)产生斥力.2)导致粒子寿命公式.3)得到衰变公式.4)弱散射.5)联系于弱电统一理论.在弱电统一理论中又应该导致斥力.进一步再结合超弦和环量子引力理论，以及引力、斥力的互相转化等.

已知粒子物理中的标准模型包含某些对称性矛盾.三代夸克-轻子偏离SU(3)对称性，按此它们应该组成对称的6个SU(2)群.如果对称性完全成立，类似于u-d是I=1/2的同位旋二重态，c-s和t-b及三代轻子(νe-e,νμ-μ,ντ-τ)也应该是I=1/2的同位旋二重态.但这与s和c夸克是两个I=0的同位旋单重态不同.笔者引入一个新的组合量子数F=I-S，它可以唯一地描述各种重子.此外，存在由相同的夸克组成核子-介子时，结合能与稳定性的矛盾，超弦的质量可达宏观标度Δm=2.209×10-2g等.

总之，粒子物理中的某些基本问题值得进一步深入研究.