基于“问题解决”下的数学课堂教学的理论与实践

何大勇（重庆市礼嘉中学校）



基于“问题解决”下的数学课堂教学的理论与实践

何大勇
（重庆市礼嘉中学校）

摘要：数学教学始终是在解决问题的过程中让学生完成对知识的理解和掌握的。把问题植入课堂，让问题成为驱动学生进一步学习和思考的动力，使学生在解决问题的过程中体会学习数学的方法。

关键词：问题解决；理论与实践；教学设计

科学始于问题，数学与“问题”有着天然的、不可分割的联系。著名教育心理学家加涅认为教育课程最终目标就是教学生解决问题。教学应当把问题植入课堂，让问题成为驱动学生进一步学习和思考的动力。

一、“问题解决”的现实价值

高中数学新课程标准倡导学生自主探索、动手实践、合作交流、阅读自学等学习数学的方式。学生的自主探索必须要有方向的引领，这个方向是根据教学内容的目标要求而确立的，实现目标又是分阶段目标来进行的。学生掌握知识就是把一个个问题进行理解和解决，问题解决了，在一定程度上就掌握了相关知识。问题解决时有学生的自主思考，有创新和发现，有学生的动手实践，有同伴的合作交流。在问题解决的过程中，让学生构建解决问题的序列步骤，最终能让学生的能力得以提升。问题解决是学生进步成长的阶梯，实施的过程是让学生体验数学发现和创造的历程。教师应当根据教学内容设计出前后有逻辑关系的问题链，让学生思考和解决，也鼓励学生自己提出问题。这个过程蕴含着充分的认知价值，为达成教学目标提供了保障。

二、怎样设计出好的数学问题

张奠宙教授在《数学素质教育设计》中对“好问题”提出了五条标准：（1）各种不同水平的学生都可以由浅入深地作出回答，不一定有终极答案；（2）对多数学生来说不是常规的，不能靠模仿来解答；（3）可以是一种情景，其中隐含的数学问题靠学生自己去提出、求解并作出解释；（4）具有趣味和魅力，能引起学生思考，激发学生挑战自己的智力；（5）解决它往往需伴以个人或小组的数学活动。

由此可见，“好问题”必须具备三个条件，即可接受性、障碍性和探究性。“好问题”不一定是大而全的问题，应当是与学生所学知识有一定的联系、对知识掌握有着支撑作用的问题。如在讲完均值不等式后给出以下几个问题让学生思考解决：求下列函数的最小值

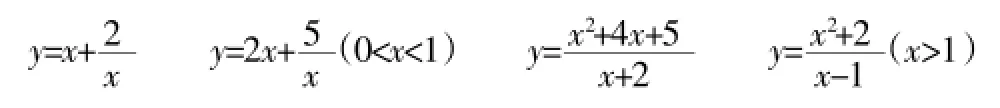
这些问题对巩固所学知识起到很好的帮助作用。

怎样设计“好问题”呢？头脑风暴法的发明人亚历克斯·奥斯本曾经为企业界专门设计一个激发发明创新的参考表，它虽然是针对开发新产品而设计的，但我们可以吸收奥斯本的思想制订一个适合于教学的问题参考表，借以设计“好问题”：（1）问题的条件可否改变？问题的结论可否加强？（2）问题的逆命题是否成立？（3）特殊问题可否引申出一般形式？（4）现有问题可否进行类比联想？（5）现有的问题正确吗？能否构造反例？（6）现有的解法是否最佳？可否运用另一种观念来思考？

基于以上认识，我们在日常教学中应该创设问题情境，通过“问题解决”达到掌握知识、提高能力的目的。对课堂教学情境中的每一个学生来说，可能产生不同的问题，这源于学生个体的基础差异，一个学生所遇到的问题可能对另外一个学生来说就不是问题，只有当学生辨别出自己的学习目标与他现在所遇的问题有距离时，才会真正形成要解决的问题。

三、基于“问题解决”的教学实践探索

通过这几年实践与反思，在实施“问题解决”教学方式的问题设计时，应当做到以下几点：

1.问题设置要贴近学生思维的“最近发展区”

问题设置是一个复杂的过程，包括许多技巧和活动。只要所提出的问题与学生已有的知识结构有关联，问题就能让学生产生联想，激发学生思考。教师一定要控制问题难度，让其“接地气”，要有“中心问题”和“子问题”，所有问题形成一个连贯的合乎逻辑的“问题链”；使问题的科学性、探究性、解决的可行性有利于学生的创新意识、实践操作能力和人文素养的形成。例如在余弦定理第一节课的教学时，可进行如下问题设计：

问题1：运用正弦定理理解三角形，学生通过思考发现可以解决以下两类问题：（1）已知三角形的任意一边及其两角；（2）已知三角形的任意两边与其中一边的对角。接着提出下面的问题：

问题2：如果已知三角形的两边及其夹角，根据全等三角形的判定方法，这个三角形是形状、大小完全确定的三角形。从量化的角度来看，如何从已知的两边和它们的夹角求三角形的第三边和其余两个角？

问题3：如右图，在△ABC中，设BC=a，AC=b，AB=c，已知a，b和∠C，求边c。

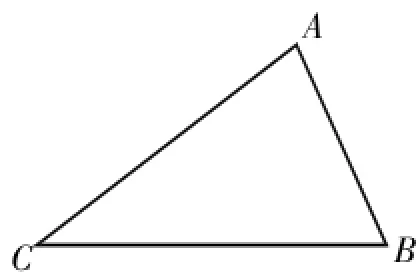
让学生在问题的驱使下主动去探索并解决问题。

2.问题要有现实性和趣味性

问题的现实性就是指问题的内容要与学生的生活背景有着直接的关联，是生活中需要应用所学知识去解决的问题，使学生感到学习数学是一种有意义的活动，从而帮助学生认识数学的价值。问题的描述和设置一定要拉近与学生的距离，语言不能枯燥干涩，一定要适合学生的年龄特征，便于学生理解，这样才能让学生感兴趣，使学生产生解决问题的欲望。我在“集合的含义与表示”这节课的教学中就提出如下问题让学生思考：有一个百货商店，第一批进货是收音机、皮鞋、尼龙袜、茶杯、闹钟，共计5个品种；第二批进货是帽子、皮鞋、热水瓶、闹钟，共计4个品种，问一共进了多少品种的货？能否回答一共进了4+5=9种呢？学生回答（不能，应为7种），然后教师和学生共同分析原因：由于两次进货有两种共同的品种，故应为4+5-2=7。然后进一步指出：这里涉及了另一种新的运算。通过设疑激趣，引发学生积极思考。

3.问题要有挑战性和思考性

学生的数学学习内容应当是富有挑战性的，问题的设置不能太简单，那种一看就知道答案的题目是不能作为问题的。我们设计的问题必须具有思考性，即这类问题应当要求解题人具有某种程度上的思辨力、独立分析力以及创造力。我在讲分步乘法原理和分类加法原理时就让学生思考这样一个问题：一个楼梯共有8步梯坎，某学生可一次上1步梯坎、2步梯坎、3步梯坎，问共有多少种不同的上楼梯方法？若将8改为n能否得到一般结论。这样的问题对学生很有挑战性。

4.问题要有开放性和层次性

开放性问题是指条件不完备、答案不确定的问题，这样的问题能给学生积极主动思考留下更广的空间，对培养学生思维的发散性有着很好的推动作用，学生的创造力不能因为问题设置不合理而受到禁锢。教师设置具有开放特征的问题，学生尝试去解决，通过添加条件或者补充遗漏结论的过程能较好地培养学生思维的严谨性和批判性，让学生逐步形成具有独立创新的思维品质。由于学生的学习基础、认知水平、学习习惯存在不同程度的差异，故设计的问题必须要有层次性。问题要有难、中、易多个层次，决不能一刀切，问题要适合各个层面学生的需要。要让每个人都有体验成功的机会，让不同层面的学生都能得到最大限度的提升。

5.问题要有预设性与生成性

在具体实施课堂教学之前，教师都要结合学生的心理特征、认知水平、知识结构以及教学目标、教学内容等诸方面来设计问题，即课前问题的预设性。学生学习是一种对间接经验的主观内化过程。教师预设的问题有可能不适应学生的认知水平，在教学实施过程中也会不断产生新的问题，这就涉及对问题的调控，教师要经过比较、选择和优化再预设问题情境，以有利于学生对知识的掌握。在教学活动中，学生作为生命主体参与其中，有的学生进行着思维的“同化”，而有的是思维上的“顺应”。这就需要教师根据学生的状况调整问题的呈现方式，有时还要临时构建问题，处理好问题的预设性和生成性。课后还需要对问题解决的效果和遗留问题进行跟踪，及时地形成反馈，发现学生在掌握知识上存在的不足并及时进行查漏补缺，同时为促进教学积累经验，对后续教学预设问题提供参考。

参考文献：

［1］张奠宙.数学素质教育设计［M］.南京：江苏教育出版社，1996.

［2］郑毓信.问题解决与数学教育［M］.江苏教育出版社，1994.

［3］郑毓信，梁贯成.认知科学建构主义与数学教育［M］.上海教育出版社，1998.

·编辑栗国花