立体几何概念的正方体模型教学法探讨
2016-08-08张红专范久良
张红专 范久良

我在每次高三总复习之前都作一次问卷调查,其中有一项为:“你认为高中数学最难学的章节有那些?”答卷中70%左右的回答有“必修2第二章”。通过调查分析,原因不外乎有四条:一是本章概念多;二是图形多;三是学生缺乏空间想象能力;四是平面几何定势思维给空间概念带来认识上的障碍。确实,在这一章的教学中教师常常费尽口舌,而学生囫囵吞枣、似懂非懂。笔者常想,如果我们在教授这一章中能找到一个具体模型,在讨论点、线、面之间的关系时,不管条件如何变化,都能帮助我们分析其位置关系,达到研究的目的,那么教与学都会感到非常轻松,这当然是一件非常有意义的研究活动。
有没有这样一个具体模型能帮助我们达到这个目的呢?正方体模型有此特征。因此笔者根据本章特点和学生的认知过程,在教授“立体几何”概念时,总结了一种“正方体模型教学法”。
一、正方体模型的特点
正方体是立体几何中最常见的几何体,由它的特征不难发现它包含了“立体几何”研究中的点、线、面元素,及直线与直线、直线与平面、平面与平面的位置关系,所以我在教学中讲授有关概念时,都先借助正方体模型进行演示,使同学们先有一个直观印象,然后再作深入的研究。
(一)正方体模型中的平面展示平面的性质
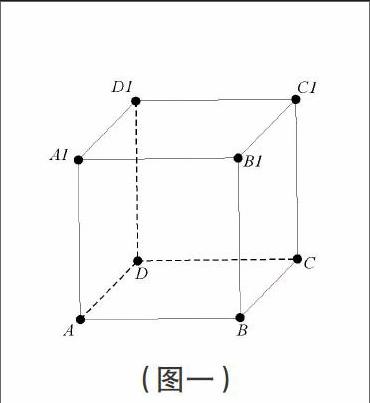
正方体模型有6个直观面和6个对角面,如图一。平面的基本性质中的三条公理、三条推论,都能很容易地从模型中演示和说明。例如平面AC和平面AB 1有一个公共点A,则平面AC和平面AB l有且只有过A点的一条直线AB,即公理2的内容。也就是说平面性质中元素及关系可由正方体模型引进。
(二)正方体模型中的线段反映两条直线的位置关系
正方体模型中有l 2条棱、1 2条面对角线、4条体对角线,这些线段共可组成378对反映直线平行、相交、异面三种关系,这些为我们学习两直线的位置关系提供了具体而丰富的实例。例如我们在学习异面直线的定义、判定、公垂线、距离、所成的角时,这类问题学生往往很难一下搞清楚,如果我们借助正方体模型中的线段,如A B与B l C l加以说明,所有问题便一目了然了。
(三)正方体模型中的直线与平面的平行和垂直
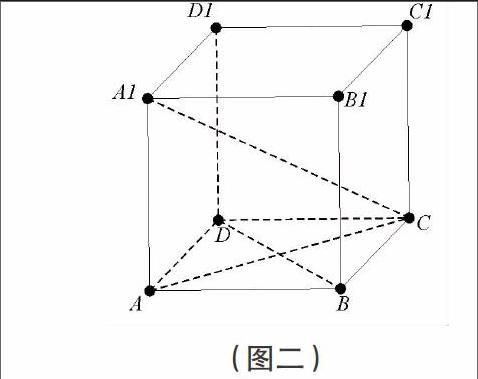
正方体中任意两条相对的棱都平行,则一条棱必平行于另一条棱所在平面;正方体中任意一条棱都垂直于不包含且和它相交的平面;直线与平面相交的关系在模型中也很直观。如图二,AAl∥BBl,则AAl //平面 BCl;AAl⊥AB,AAl⊥AD,则AAl⊥平面AC;AAl⊥平面AC,BBl⊥平面AC,则 AAl∥BBl 。又∠AlCA为AlC与平面AC所成的角;Al C,AAl,AC,B D构成三垂线定理模型等等。凡直线与平面位置关系中所涉及的概念都能在正方体模型中找到直观图。
(四)正方体模型中的平面与平面
正方体相邻两个面都相交,不相邻两个平面都平行,例如AlBl,AlDl 平面Al Cl,且AlBl∥平面AC, Al Dl//平面AC,则平面AlCl∥平面AC,相邻表面,对角面与表面,对角面之间都构成二面角模型。例如:平面AC—BC—平面AlC构成二面角模型,∠ABAl为二面角平面角;同样两平面垂直的判定与性质也可用正方体模型直观说明。因此平面和平面的位置关系也可由正方体模型中的面直观看到。
二、正方体模型教学法的基本模式
正方体模型教学法的大框架是:分析概念的条件和结论——借助正方体模型线面关系——解答问题。对具体课堂教学来说又可分为下述几个环节。
(一)直接反映概念的基本特征
正方体模型中的线面关系,可直接传递有关概念的内容,并且它给学生的信息是直觉的、显示结构的、完整的,它能使学生正确地理解概念的内涵,甚至单凭图形的直观现象,就能理解概念,无需语言文字描述,这是其他一些传播媒介所不及的。例如异面直线的画法和公垂线及两异面直线的距离问题,对于初学者来说是很难搞清楚的,而我们借助正方体模型中的有关线段,例如AB与CDl,它们为异面直线,BC为公垂线,|BC|即为异面直线的距离,AB与CDl位置关系能更好地反映异面直线的画法,以及既不相交又不平行的特征。
(二)借助模型分析、判断,变化图型观察方式
我们在分析立体几何问题时,若没有图形,学生便感到困惑。自己作图,空间图形有时便变成了平面图形,不具直观性。在没有图形时我们若能借助正方体模型分析、判断,然后再推广到一般情形,这样就能帮助我们作好由“无形”到“有形”的过渡。具体来说就是:解决一个问题,先在正方体模型中找到具有题设条件的线和面,再仿照它画成直观图,然后还可根据正方体特殊线面关系来分析一般属性,达到解决问题的目的。例如在巩固直线与平面平行的判定与性质的概念时,有一道这样的题目:一条直线与两相交平面都平行,那么这条直线与两平面的交线平行。若我们借助正方体模型中的AA1与平面BC1、平面CDl进行分析,再把它转化为一般性质的模型,这样作出了图形,证明也就容易多了。
当然若考虑任何问题都以同一形态出现,易使学生产生思维定势。如我们多数学生不能灵活地在不常见位置上运用三垂线定理。所以我们运用“正方体模型教学法”,指导学生改变其观察方式,这样便更能拓广其空间想象能力。例如在正方体模型中我们能发现4条体对角线与不相交的l 2条面对角线之间是同一种位置关系;正方体每个面都可看成三垂线定理中的射影面。
(三)正方体模型的化归变换
正方体模型虽然能反映各种位置关系,但势必都是特殊关系,有相当的必然和偶然成份,且有它的局限性。我们在教学中可依赖它、应用它,但一定要过渡到变化它。这也正是这种教学法研究的一个主要目的。也就是说正方体模型要拓广成为一般的空间图形;非正方体模型可通过分割或镶补的手段转化为正立方体模型,用正方体的特点快速寻求正确的结果。例如在平行六面体中,过交于同一顶点的三条棱中点的平面截平行六面体,求截得的三棱锥体积是平行六面体的多少倍?通过观察正方体是平行六面体的特殊情况,那么平行六面体的特征,在正方体中一定能实现,这个问题自然就把平行六面体特殊化为棱长为1的正方体,这样过正方体的相邻三条棱中点的平面截正方体,得一正三棱锥,又例如图四1,过正方形ABCD的顶点D作PD⊥平面ABCD,设PD=AD=a,求面PAB与面PCD所成二面角大小。这个问题虽然从表面上看是四棱锥问题,但稍作分析,它便是正方体模型的一部分,将原四棱锥可以补成正方体如图四2,则不难发现∠DPA为二面角的平面角,所以答案为 ,这样化归为正方体模型解题比常规方法要简捷得多。
三、正方体模型教学法的特点
(一) 联系实际,丰富感知,遵循从特殊到一般的规律
概念都是从个别特殊的结论归纳出来的,图形亦是如此。立体几何概念的内涵若是能从典型的模型中找出反映其内涵的线面关系,那么我们掌握它便能更直接、更具体,这样通过实物与图形、整体与局部对照,可使学生逐渐把反映概念的图形立体化、形象化。例如学习三垂线定理,我们使用正方体模型中的三垂线来研究,这样学生能更快地接受并掌握。正方体模型教学法正是由典型模型中的线面关系来反映概念的内涵,使学生从具体模型上掌握概念,为进一步深刻认识打好基础。
(二)训练了学生识图、作图能力
正方体模型立体感强,反映的关系多,正方体模型教学法便是教会学生在作图时利用正方体模型中面线衬托方式,或辅助位置关系,来掌握画立体图的原理、方法和技能,从而使画出来的图形立体化、直观化。
(三)强化概念、定理的引入,突出第一感知的印象
学生在学习中,会遇到很多新问题、新矛盾,第一次触及这些事物时的认识很易形成“先入为主”的思维定势,这对形成正确的空间概念关系很大,并影响着后续内容的学习。因此,在学习概念、定理时,抓好起点,建立有代表意义的模型,突出他们的本质属性,就能克服各种各样的困惑,获得更多、更新的认识。而正方体模型能反映各种线面关系,且图形直观、易画。因此在讲解概念的教学活动中,运用正方体模型教学法,用正方体模型中的线、面关系,进行深刻的剖析,获得第一感知的印象,也就获得了正确的认识。例如讨论三个平面两两垂直,则三条交线两两垂直的问题,当然首先想到是用正方体模型进行分析。
(四)抓住实质,由浅入深,突出概念内涵,逐步完善空间概念
立体几何中概念多,且逐渐深化,交错出现,相辅相承,使学生感到难学。我们在讲授概念时,只要学生初步理解,基本上能用,就算达到了开始的教学要求,应该不奢求一次性讲深讲透、一步到位。在讲授概念时,运用正方体模型教学法,从大家非常熟悉的正方体模型入手,这样就会很快地使学生创造一个能理解、会作图、易证明的思维环境来接受这些概念。在接受了这些基本概念的基础上,再引申拓广便不是难事了,空间概念便会逐步完善。
四、实施“正方体模型教学法”的几点体会
(一)提高了学生们的学习兴趣,加强了概念理解能力
未实施此教学法时学生感到立体几何难学、不会学,实施此教学法后,学生感到空间概念并不难建立,多种位置关系也很容易搞清楚,掌握概念也无需死记硬背了。运用此教学法在讲授概念时,学生能主动思考问题,从多角度解决问题。对于理解力较差的学生,由于教法改进,学有所得,增强了学几何的信心,激发了他们的学习热忱,对概念的理解掌握也较快了。这样较好地克服了学习立体几何的两极分化,从而使学习立体几何整体成绩相应提高了许多。
(二)提高了思维能力,增强了课堂效益
此教学法既培养了学生思维定势的学习方法,也培养了学生从不同角度独立思考、勤于探索的能力,培养了学生分析和解决问题的能力。我们借助的是立体概念较强的几何体,能有效地防止平面几何概念向立体几何概念的负面迁移。同时,同学们能有效地快捷地掌握概念,为学习其他知识打下坚固的基础,大大地提高了课堂效益。
(三)有待探讨的一些问题
此教学法虽然取得了一定的成效,但在实验过程中还有一些问题,如思维定势带来的负面影响、立体模型中线面关系都是特殊关系,带有一定的偶然结果、局限性也很明显等等。对这些问题的改进和解决有待进一步的研究探讨。
(作者单位:湖南大学附属中学)
