基于多元线性回归血压影响因素分析

孙 波安徽财经大学统计与应用数学学院 安徽蚌埠 233030



基于多元线性回归血压影响因素分析

孙 波
安徽财经大学统计与应用数学学院 安徽蚌埠 233030

【摘要】血压的高低与健康息息相关，血压低易造成头晕、乏力、面色苍白，工作能力下降等，血压高导致各种心脑血管疾病、肾脏疾病。本文建立多元线性回归模型分析年龄、体重指数、吸烟习惯与血压的线性关系，从而对如何控制血压稳定提出参考。

【关键词】血压；影响因素；多元线性回归

一、多元线性回归模型

首先做出散点图分析血压与年龄、血压与体重指数（体重kg/身高m的平方）之间的关系，如下所示：

图1　血压与年龄、体重指数的散点图

从图中可以看出：（1）随着年龄的增长血压有增高趋势，随着体重增长血压也有增高趋势；（2）总体上血压与年龄、血压与体重指数存在一定的线性相关关系。

建立多元线性回归模型：

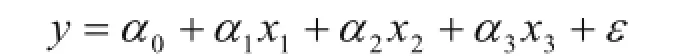
其中，a0，a1，a2，a3是回归系数，ε是随机误差。结果如表（1）：

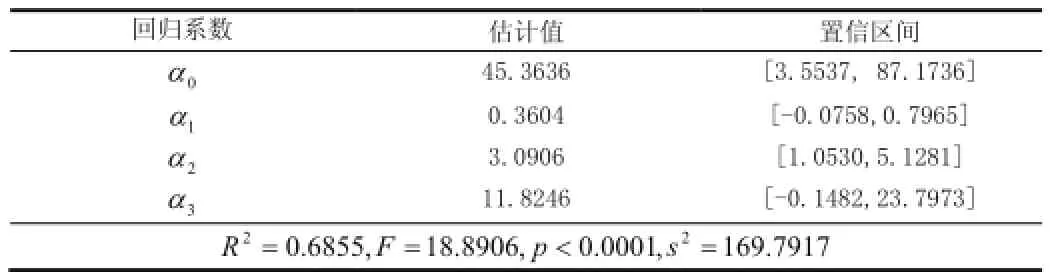
表1　回归模型的系数、置信区间与统计量

由表知a1，a3的置信区间包含零点，需要改进模型，通过残差置信区间图，剔除异常点后得到改进后的回归模型，结果如表2

表2　改进后回归模型的系数、置信区间与统计量

由上表知，此时所有参数置信区间不包含零点，F统计量增大，可决系数从0.6855增大到0.8462，得回归模型为

最后，对模型进行检验，说明模型合理性。

（1）残差正态检验：进行j b t e s t检验与t检验，h=0,h1=0,p1=1，故残差服从均值为零的正态分布。

（2）残差异方差检验。进行Goldfeld-Quant检验，将28个数据从小到大排列，去掉中间6个数据，得到F统计量观测值f=1.6604，F（7，7）=3.79，可知f＜F，不存在异方差。

（3）残差自相关性检验。进行D-W检验，D=1.4330，查阅表得dl=0.97,du =1.41，因为du＜DW ＜4−du，所以残差不存在自相关性。

二、结论

由模型结果知，年龄增加1岁，血压平均升高0.4303/mmHg，体重指数上升1个单位，血压平均升高2.3449/mmHg，另外，长期吸烟对血压的变化影响巨大。

因此，对于中老年人，要注意控制体重，改掉吸烟的习惯，从而避免血压过高，出现疾病；对于偏瘦的年轻人，适当增重，从而保持血压的正常。

参考文献

［1］张宇山.多元线性回归分析的实例研究［J］.科技信息，2009（9）.

［2］吴礼斌.经济数学实验与建模［M］.国防工业出版社，2013.06.

［3］卓金武.Matlab在数学建模中的应用［M］.北京航空航天大学出版社，2014.09.