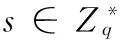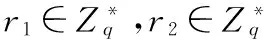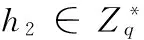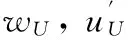两种无证书签密方案的密码分析和改进

樊爱宛　潘中强　赵伟艇

1(平顶山学院软件学院　河南 平顶山 467002)2(平顶山学院网络计算中心　河南 平顶山 467002)



两种无证书签密方案的密码分析和改进

樊爱宛1潘中强2赵伟艇1

1(平顶山学院软件学院河南 平顶山 467002)2(平顶山学院网络计算中心河南 平顶山 467002)

摘要对两种新提出的无证书安全签密方案进行密码学分析，证明这两种方案都是不安全的。对于第一种方案，不仅使主密钥泄露，而且在类型Ⅰ和类型Ⅱ敌手攻击下是无法保证机密性和抗伪造性。对于第二种方案，在类型Ⅰ敌手攻击下，不仅可以利用公钥替换伪造任何用户对任意消息的签密，而且可以冒充合法接受者解签密消息。利用公钥与哈希函数绑定、增加随机数和公钥配对参与运算的方法，分别对它们进行改进。在随机预言机模型中，对改进方案进行安全性证明，表明改进方案是安全的。

关键词无证书签密机密性攻击伪造性攻击公钥替换随机预言机模型

0引言

1997年，Zheng[1]提出的签密思想解决了先签名后加密的计算效率低的问题，其思想是将加密和签名融合于一个逻辑步骤里，同时实现信息的机密性和不可否认性。2003年，Al-Riyami等[2]提出了无证书的密码系统解决了公钥复杂的证书管理和密码托管问题，其思想是利用密钥生成中心KGC(Key Generation Center)产生用户的部分私钥与用户随机选择的秘密值，共同组成用户公钥对与私钥对。基于签密与无证书的高效性和强安全性等特点，2008年Barbosa 等[3]开始将无证书密码系统应用于签密思想中，提出了无证书签密方案。

近年来，一些无证书签密方案被相继提出。2009年，Sharmila[4]指出Barbosa 等人的方案存在漏洞，其所提出的方案不能保证保密性和不可否认性。2010年，Selvi等[5]针对Xie等[6]提出的无证书签密方案进行分析，指出其方案无法抵抗Type I攻击。2011年刘文浩等[7]利用离散对数难解问题，提出了一种不使用双线性对的无证书签密方案。然而，Shi等[8]证明了该方案存在签名的选择性伪造攻击和密文机密性问题。2014年，Zhou等[9]提出的一可证明的安全无证书签密生成方案，Shi等[10]设计了一个安全的无证书线上线下签密方案。然而，这些方案都采用了双线性对计算方式，运算效率偏低。

最近，夏昂等[11]和高健鑫等[12]分别提出了高效安全无线性对的无证书签密方案(以下简称XZ方案和GAO方案)，并通过形式化证明了方案的安全性。本文通过对XZ方案和GAO方案分析，发现对于XZ方案，不仅使主密钥泄露，而且在类型Ⅰ和类型Ⅱ敌手攻击下是无法保证机密性和抗伪造性。对于GAO方案，类型Ⅰ敌手可以利用公钥替换伪造任何用户对任意消息的签密。针对以上两种方案的安全缺陷，分别进行了改进，并在随机预言模型下证明了改进方案在适应性选择消息攻击下是具有不可伪造性和加密不可区分性。

1预备知识

1.1数学难解问题

定义1离散对数问题(DLP)：两个大素数q(0

定义2计算Diffie-Hellman问题(CDHP)：两个大素数q(0

1.2无证书签密系统及安全模型

一个无证书签名系统由7个算法组成：系统初始化、部分密钥生成、设置秘密值、设置私钥、设置公钥、签密和解签密。

在无证书签密系统中存在2种攻击者。

Type Ⅰ：攻击者A1无法获取KGC的主密钥s，但是可以任意替换公钥。此类型主要是模仿非法用户进行的攻击。

Type Ⅱ：攻击者A2可以获取KGC的主密钥s，但是不可以任意替换公钥。此类型主要是模仿能够为用户生成部分密钥的KGC进行的攻击。

无证书签密的安全模型及攻击者的基本攻击询问方式可见文献[7]。

2对XZ方案的安全性分析及改进

2.1XZ方案描述

设置公钥用户A的公钥为PKID= (XA, YA)。

设置私钥用户A的私钥为SKID=(xA, yA)。

(1) 选取k，计算R = k yAYB。

(2) 计算W = YB(dA+ H2(IDA, IDB))。

(3) 计算t= (k yA) /xA；v= H3(W, IDA)⊕(m‖R‖t)。

(4) 发送消息签密结果σ=(t, v)。

解签密解签密者B按如下方式处理身份为IDA的用户A发送签密结果：

(1) 计算W′= yB(XA+ H1(IDA, XA)P + H2(IDA, IDB) Ppub)。

(2) 计算m= H3(W′, IDA)⊕v，得到R和t。

(3) 计算t yBXA= R等式是否成立。若成立则接受m，否则拒绝。

2.2XZ方案安全性分析

经过安全性分析发现，XZ方案既不能保证KGC主密钥的安全，也无法抵抗伪造性和机密性攻击，更无法保证前向安全性。

1) KGC主系统密钥的泄露

XZ方案中，用户A在签密过程中利用KGC的秘值xA，参与了t= (k yA) /xA的计算。由于dA=xA+ H1(ID, XA)s，用户A在知道dA，xA和 H1(ID, XA)值的基础上，能够计算出KGC的主系统密钥s。

2) 伪造性攻击

XZ方案不能抵抗TypeⅡ伪造性攻击。具体攻击如下：

(1) A2已知主系统密钥s和部分私钥dA，根据dA=xA+ H1(ID,XA)s，求出xA。

(2) A2随机选取t，计算R=t xAYB。

(3) A2计算W= YB(dA+ H2(IDA, IDB))。

(4) A2计算v= H3(W, IDA)⊕(m‖R‖t)。

(5) A2冒充用户A发送消息签密结果v。

敌手A2伪造的签密结果，能够通过W′= zB(XA+ H1(IDA, XA)Ppub+ H2(IDA, IDB)P)进行解密，具体证明如下：

W′=YB(dA+H2(IDA,IDB))

=zBP(dA+H2(IDA,IDB))

=zBP(xA+sH1(IDA,XA)+H2(IDA,IDB))

=zB(XA+H1(IDA,XA)Ppub+H2(IDA,IDB)P)

=W

接收方B通过H3(W, IDA)⊕v，求解出m，R和t。敌手A2伪造的签密也能够通过t zBXA= R等式的判断，从而使接收方对消息进行接收。具体证明如下：

tzBXA=tzBxAP=txAYB=R

由以上分析可知，伪造的签密可以满足验证式，即敌手A2伪造的签密是有效的。

3) 机密性攻击

XZ方案在Type Ⅰ下无法抵抗A1公钥替换的机密性攻击。具体攻击如下：

若A1获取了用户A发送签密消息v，则执行以下步骤：

(2) 计算m= H3(W′, IDA)⊕v，得到R和t。

敌手A1冒充用户B接收的签密结果，一定能够通过接收方的W′= zB(XA+ H1(IDA, XA)Ppub+ H2(IDA, IDB)P)和发送方W = YB(dA+ H2(IDA, IDB))两个等式的判断。

4) 无法保证前向安全性

假设敌手得到某一次的σ=(t, v)及W，那么就可以利用W解签密以后的签密结果。这是因为W = YB(dA+ H2(IDA, IDB))，W的求解是固定的，并没有随着每次会话的改变而改变。

2.3改进方案的描述

签密过程如下：

(1) 选取r，计算R = rP。

(2) 计算kA= H2(IDA, XA, YA, Ppub) ；kB= H2(IDB, XB, YB, Ppub) ；hB= H1(IDB, XB)。

(3) 计算W =r(kBYB+ XB+ hBPpub)；v= H3(W)⊕m。

(4) 计算h = H4(IDA, XA, YA, R, v, W, m) ；t=[( kAzA+ dA)/( r+h)] mod q。

(5) 发送消息签密结果σ=(R, v, t)。

解签密过程如下：

(1) 计算kA= H2(IDA, XA, YA, Ppub) ；kB= H2(IDB, XB, YB, Ppub) ；hA= H1(IDA, XA)。

(2) 计算W = (kBzB+ dB)R；m= H3(W)⊕v。

(3) 计算h = H4(IDA, XA, YA, R, v, W, m)。

(4) 判断t(R +hP)= kAYA+ XA+ hAPpub等式是否成立。若成立则接收m，否则拒绝。

改进说明：

(1) 针对KGC产生的xA导致主密钥泄露的问题，改进方案采用不再将xA参与用户签密运算的方式进行解决。

(2) 针对对称密钥无法保证签密的前向安全性的问题，改进方案采用用户随机产生的r参与每次会话对称密钥的产生运算的方式进行解决。

(3) 针对Type Ⅰ下的机密性攻击和TypeⅡ下伪造性攻击成功的原因：KGC产生的部分公钥和用户产生的部分公钥无法相互制约，改进方案采用均有发送方与接收方的公钥对与私钥对参与的方式进行解决。

3对GAO方案安全性分析及改进

3.1方案描述

设置私钥将系统参数params、DA和skA作为输入值，用户A生成私钥SKA。 SKA=(DA, skA)= (tA, zA)。

设置公钥将系统参数params、PA和pkA作为输入值，用户A生成公钥PKA=(PA, pkA)= (wA, uA)。

(3) 计算c= E((wBuByh1)r1, ( r2, m))。

(4) 返回σ=(h,s,c)。

解签密假设一个签密信息=(h,s,c)，发送方用户A的身份为IDA，公钥为PKA，接收方用户B的身份为IDB，公钥为PKB，私钥为SKB，用户B根据以下步骤生成解签密信息δ，并进行接受明文信息或者拒绝的操作:

3.2方案安全性分析

经过安全性分析发现，GAO方案既无法抵抗伪造性和机密性攻击，也无法抵抗机密性攻击。

1) 不可伪造性

Type Ⅰ攻击者A1对GAO方案进行伪造攻击，具体攻击如下：

(5) 计算c=E((wBuByh1)r1, ( r2, m))。

(6) 返回σ= (h, s, c)。

由于：

=g(a+h)s(zB+tB)

=gr1(zB+tB)

=(gzBgsB+sH1(IDB,wB))r1

=(gzBgtB)r1

=gr1(zB+tB)

并且：

所以，伪造的签密信息能够通过用户B的验证。由此可见，A1通过以上步骤可以伪造一个合法的消息，GAO方案不具有不可伪造性。

2) 机密性

Type Ⅰ攻击者A1对GAO方案进行机密性攻击，具体攻击如下：

(6) 返回σ= (h, s, c)。

攻击者A1可以根据下列式子得出R的值。

R=gr1=(wAuAyH1(IDA,wA)gh)s

攻击者A1可以根据下列式子得出m的值。

=D((gb)r1,c)

=D((gr1)b,c)

所以，签密信息能够被攻击者A1解签密。由此可见，A1通过以上步骤可以冒充接收方并得到一个合法的消息，GAO方案不具有机密性。

3.3改进方案的描述

签密：

(2) 计算h1= H1(IDB, wB)，hA= H2(IDA, wA, uA, y)，hB= H2(IDB, wB, uB, y)。

(3) 计算ξ = (wBuBhByh1)r1，c = E(ξ, m)，h = H3(m, R, IDA, wA, uA,ξ)。

(5) 返回σ= (R, s, c)。

解签密：

(1) 计算h1= H1(IDB, wB)，h2= H1(IDA, wA)，hA= H2(IDA, wA, uA, y)，hB= H2(IDB, wB, uB, y)。

(2) 计算ξ=(R)hBzB+tB，m = D(ξ, c)，h = H3(m, R, IDA, wA, uA,ξ)。

改进说明：

(1) 针对机密性攻击的问题，改进方案在产生通信对称密钥ξ = (wBuBhByh1)r1，相对于原方案(wBuByh1)r1，利用hB防止uB的公钥替换。

4改进方案的安全性分析

限于篇幅，本文仅对GAO的改进方案进行安全性分析。XZ的改进方案可以采用类似方式处理，但是GAO改进方案的证明是以离散对数的DLP和CDHP计算困难性为基础的。而XZ改进方案的证明是以椭圆曲线的DLP和CDHP计算困难性为基础的。

定理1在计算DLP困难和随机谕言模型的假设下，改进方案在适应性选择消息攻击下是存在性不可伪造的。此定理由引理1和引理2推导出。由于两个引理的证明相似，为了节约空间，仅给出引理1的具体证明。

引理1假设一个Type Ⅰ攻击者A1以不可忽略的概率赢得了Game 1的胜利，则存在一个算法C，以一个不可忽略的概率解决DLP难题。

初始化C计算y=ga，params=(q, p, g, y, H1, H2, H3, E, D)。C将params发送给A1。

公钥询问C构建公钥列表(IDU, wU, uU)。A1向C提出IDU的询问，C以下面步骤进行回答：

(1) 如果C的公钥列表中存在IDU，C向A1返回PKU= (wU, uU)。

秘密值提取A1向C提出IDU的询问，C以下面方式进行回答：

(1) C以IDU为参数，运行公钥查询，在公钥列表中得到(IDU, wU, uU)。

(2) C查找私钥列表(IDU, zU, tU)，将zU返回给A1。

部分秘钥提取A1向C提出IDU的询问，C以下面方式进行回答:

(1) C以IDU为参数，运行公钥查询，在公钥列表中得到(IDU, wU, uU)。

(2) 如果IDU≠ID*，C查找私钥列表(IDU, zU, tU)，将zU返回给A1。

(3) 如果IDU=ID*，C返回“⊥”，并终止算法。

(1) C以IDU为参数，运行公钥查询，在公钥列表中得到(IDU, wU, uU)。

签密C构建签密列表(IDS, PKS, IDR, PKR, m,σ)。其中S为发送方身份，R为接收方身份。A1向C提出(IDA, PKA, IDB, PKB, m)的询问，C以下面方式进行回答：

(1) 如果IDA≠ID*，C依据方案的签密算法，计算σ= (R, s, c)，将结果添加到签密列表，并将σ返回给A1。

解签密A1向C提出(IDA, PKA, IDB, PKB,σ)的询问，C以下面方式进行回答:

(1) 如果IDB≠ID*，C依据方案的解签密算法，将m返回给A1。

(2) 如果IDB=ID*，且IDA≠ID*，C检查是否有(IDA, PKA, IDB, PKB, *,σ)是否在签密列表中，若存在C将对应的m返回给A1，否则返回“拒绝”。

最后，A1输出σ= (R, s, c)。如果IDA≠ID*，C返回“⊥”，并终止算法。如果IDA=ID*，且IDB≠ID*，C返从私钥列表和公钥列表中查找(IDB, zB, tB)和(IDA, wA, uA)，其中公钥PKA= (wA, uA)已经被A1替换。C可以通过m=D((R)hBzB+tB,c)得到明文。通过伪造引理可得，如果对C算法采用随机参数不变，选择不同随机谕言机H1和H2的方式进行回放，A1就能得到3个不同的签名ψ(i)= (R, s(i))，i=1,2,3。由于以上签名是有效的，所以下面的等式是成立的。

R = (uAhA (i)wAyh2 (i)gh(i))s(i)

通过r1、 zA、 sA和a能够计算R、 wA、 uA和y：R = gr1, wA= gsA, uA= gzA, y = ga。从以上分析，可以得到如下等式：

r1= zAhA(i)s(i)+ sAs(i)+ ah2(i)s(i)+ h(i)s(i)

在以上等式中r1、 zA、 sA和a都是未知的，C从以上线性无关方程组中求解这些值，从而输出a，难度相当于求解DLP难题。如果对方案攻击成功的概率是不可忽略，则C能够以不可忽略的概率解决DLP问题。所以，本方案在计算DLP困难和随机谕言模型的假设下，改进方案在适应性选择消息攻击下是存在性不可伪造的。

引理2假设一个TypeⅡ攻击者A2以不可忽略的概率赢得了Game 2的胜利，则存在一个算法C，以一个不可忽略的概率解决DLP难题。

定理2在计算CDHP困难和随机谕言模型的假设下，改进方案在适应性选择消息攻击下是具有加密不可区分性。此定理由引理3和引理4推导出。由于两个引理的证明相似，为了节约空间，仅给出引理4的具体证明。

引理3假设一个TypeⅠ攻击者A1以不可忽略的概率赢得了Game 3的胜利，则存在一个算法C，以一个不可忽略的概率解决CDHP难题。

引理4假设一个TypeⅡ攻击者A2以不可忽略的概率赢得了Game 4的胜利，则存在一个算法C，以一个不可忽略的概率解决CDHP难题。

证明假定一个TypeⅡ攻击者A2以不可忽略的概率ε赢得了Game 4的胜利，需要构造一个算法C，利用A2解决CDHP难题。C收到一个CDHP难题实例(p, q, g, ga, gb)，目标是能够计算出gab。C回答H1询问、H2询问和H3询问，询问与回答方式与引理1相同。其他询问回答方式如下：

公钥询问C构建公钥列表(IDU, wU, uU)。A1向C提出IDU的询问，C以下面步骤进行回答：

(1) 如果C的公钥列表中存在IDU，C向A1返回PKU= (wU, uU)。

秘密值提取A2向C提出IDU的询问，C以下面方式进行回答：

(1) C以IDU为参数，运行公钥查询，在公钥列表中得到(IDU, wU, uU)。

(2) 如果IDU≠ID*，C查找私钥列表(IDU, zU, tU)，将zU返回给A2。

(3) 如果IDU=ID*，C返回“⊥”，并终止算法。

部分秘钥提取A2向C提出IDU的询问，C以下面方式进行回答：

(1) C以IDU为参数，运行公钥查询，在公钥列表中得到(IDU, wU, uU)。

(2) C查找私钥列表(IDU, zU, tU)，将tU返回给A2。

签密C构建签密列表(IDS, PKS, IDR, PKR, m,σ)。其中S为发送方身份，R为接收方身份。A2向C提出(IDA, PKA, IDB, PKB, m)的询问，C以下面方式进行回答:

(1) 如果IDA≠ID*，C依据方案的签密算法，计算σ= (R, s, c)，将结果添加到签密列表，并将σ返回给A2。

解签密A2向C提出(IDA, PKA, IDB, PKB,σ)的询问，C以下面方式进行回答：

(1) 如果IDB≠ID*，C依据方案的解签密算法，将m返回给A2。

(2) 如果IDB=ID*，且IDA≠ID*，C检查是否有(IDA, PKA, IDB, PKB, *,σ)是否在签密列表中，若存在C将对应的m返回给A2，否则返回“拒绝”。

如果对方案攻击成功的概率ε是不可忽略，则C能够以不可忽略的概率解决CDHP问题。所以，在计算CDHP困难和随机谕言模型的假设下，改进方案在适应性选择消息攻击下是具有加密不可区分性。

5结语

对两个无证书签密方案进行了密码分析，发现对于XZ方案，不仅使主密钥泄露，而且在类型Ⅰ和类型Ⅱ敌手攻击下是无法保证机密性和抗伪造性。对于GAO方案，类型Ⅰ敌手可以利用公钥替换伪造任何用户对任意消息的签密。针对以上两种方案的安全缺陷，分别进行了改进，并在随机预言模型下证明了证明改进方案在适应性选择消息攻击下是具有不可伪造性和加密不可区分性。从目前研究进展来看，如何构造安全高效的无证书签密仍然是一个亟待解决的问题。

参考文献

[1] Zheng Y.Digital signcryption or how to achieve cost(signature & encryption)<

[2] Al-riyami S,Paterson K.Certificateless public key cryptography[C]//Proc of Asiacrypt 2003.Springer-Verlag,Berlin,2003:452-473.

[3] Barbosa M,Farshim P.Certificateless signcryption[C]//Proc of ACM Symposium on Infomation,Computer and Communications Secu-rity.New York:ACM Press,2008:369-372.

[4] Sharmila S,Deva S.Efficient certificateless online/offline signature with tight security[J].Journal ofinternet services and information security,2013,1(1/2):115-137.

[5] Selvi S,Vivek S S,Ragan C P.Certifieateless KEM and hybrid signcryption schemes revisited[C]//Proceeding of ISPEC 2010.LNCS 6047,Berlin:Springer-Verlag,2010:294-307.

[6] Xie W,Zhang Z.Certifieateless signcryption without pairing[EB/OL].2010-06-20.http://epfint.iacr.org/2010/187.

[7] 刘文浩,许春香.无双线性配对的无证书签密方案[J].软件学报,2011,22(8):1918-1926.

[8] Shi W,Kumer N,Gong P,et al.Cryptanalysis and improvement of a certificateless signcryption scheme without bilinear pairing[J].Frontiers of Computer Science,2014,8(4):656-666.

[9] Zhou C,Zhou W,Dong X,et al.Provable certificateless generalized signcryption scheme[J].Designs,Codes and Cryptography,2014,71(2):331-346.

[10] Shi W,Neeraj K,Gong P,et al.On the security of a certificateless online/offline signcryption for Internet of Things[J].Peer-to-Peer Networking and Applications,2014,74(8):101-120.

[11] 夏昂,张龙军.一种新的无双线性对的无证书安全签密方案[J].计算机应用研究,2014,31(2):532-535.

[12] 高键鑫,吴晓平,秦艳琳,等.无双线性对的无证书安全签密方案[J].计算机应用研究,2014,31(4):1195-1198.

收稿日期：2015-01-27。河南省高校青年骨干教师资助计划项目；河南省科技攻关计划基金项目(152102210193)；河南省高等学校重点科研项目(15A520091)。樊爱宛，副教授，主研领域：信息安全。潘中强，副教授。赵伟艇，教授。

中图分类号TP309

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.070

CRYPTANALYSIS AND IMPROVEMENT OF TWO CERTIFICATELESS SIGNCRYPTION SCHEMES

Fan Aiwan1Pan Zhongqiang2Zhao Weiting1

1(SchoolofSoftware,PingdingshanCollege,Pingdingshan467002,Henan,China)2(CenterofNetworkandComputer,PingdingshanCollege,Pingdingshan467002,Henan,China)

AbstractApplying the cryptanalysis to two newly presented certificateless secure signcryption schemes, it is proved that both of them are insecure. For the first one, not only the master key can be disclosed, it cannot ensure the confidentiality and anti-forgery capability under the attacks made by type I and type II adversaries as well. For the second scheme, under the attack launched by Type I adversary, not just the public key can be used to replace and forge the signcryption by any user on arbitrary message, but the legitimate recipient can also be feigned to calculate the signcryption. We improved these two schemes separately by means of binding the public key and hash function, increasing the random numbers and participating in operation with public key pair. In random oracle model we proved the security of the improved schemes, they were demonstrated secure.

KeywordsCertificateless signcryptionConfidentiality attackForgery attackPublic key replacementRandom oracle model