基于数字标牌广告数据的兴趣点推荐算法研究

解贵龙　张　珣　于重重　赵　霞

(北京工商大学计算机与信息工程学院　北京 100048)



基于数字标牌广告数据的兴趣点推荐算法研究

解贵龙张珣*于重重赵霞

(北京工商大学计算机与信息工程学院北京 100048)

摘要为了解决数字标牌广告投放的推荐问题，研究基于位置数据的推荐算法。在已有的基于矩阵分解思想的兴趣点推荐算法基础上，提出结合矩阵分解思想和商业地理信息数据的兴趣点推荐模型，并在基于位置的数字标牌广告数据上进行实验。实验结果表明，通过为矩阵分解附加商业地理信息的方法，解决了位置访问数据稀疏性的问题，并为数据类型单一，推荐依据不足的问题提供了有效的数据参考及实现方法。为数字标牌广告投放提供了重要的参考依据。

关键词兴趣点推荐数字标牌位置推荐矩阵分解

0引言

数字标牌是一种全新的媒体概念， 指的是在大型商场、超市、酒店大堂、饭店、影院及其他人流汇聚的公共场所，通过大数字标牌终端显示设备，发布商业、财经和娱乐信息的多媒体专业视听系统[1]。然而，传统的数字标牌的选址，广告的投放均由人工完成，时效性低、缺乏参考依据、已经不能满足广大广告主和媒体商的利益需求[2]。因此，构建广告精准投放推荐模型，为广告主用户提供广告牌的推荐，实现广告商和媒体商的利益最大化，成为值得研究的课题。本文所研究的兴趣点推荐即可为广告投放方提供有关数字标牌的地理属性和商业属性的分析结果，从而达到广告在时间、空间、个性化上精准投放的目的。

本文所要研究的兴趣点推荐是推荐领域比较新的研究点，其中一个重要特性就是位置数据，访问或签到，它可以看成推荐系统中常见的隐式评分数据。隐式评分是相对于显示评分而言的，它不需要用户额外行动，而是根据用户行为判断对待推荐物品的喜好或厌恶程度。而对这种隐式数据的处理主要是量化这种喜好或厌恶程度的操作。2010年Ye Mao等人利用用户社交好友的协同评分和通过距离衡量好友之间的相似性进行兴趣点推荐[3]，但此方法忽略了隐式数据的处理。2012年Cheng Chen等人基于用户签到频率，利用矩阵分解思想进行兴趣点推荐[4]，很好地处理了隐式数据，但是并没有考虑到地理特征等其他因素的影响。同时还有些工作利用这些位置信息通过对空间聚集效应建模来帮助位置推荐[5,6]，但是这些方法是独立于协同过滤的。2014年Lian De-Fu等人在此基础上提出了基于地理建模内嵌的加权矩阵分解方法进行兴趣点推荐[7]，扩展了地理特征因素，并为可能添加的其他因素提供了一种方法。

本文研究的兴趣点推荐，主要针对广告-兴趣点矩阵稀疏性处理及数字标牌位置数据的特性分析处理这两个问题展开。针对于以上两个问题，本文基于Lian De-fu等人提出的GeoMF算法[7]，结合数字标牌数据特点，提出一种考虑位置的社会经济数据作为推荐指标的推荐算法，该算法较有效地解决了上述问题。

1基于位置广告数据的兴趣点推荐算法

1.1基本矩阵分解推荐算法

运用矩阵分解做推荐面临最大的挑战是数据的稀疏性。对于缺失的评分，可以转化为基于机器学习的回归问题，也就是连续值的预测，矩阵分解如下：

(1)

(2)

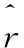
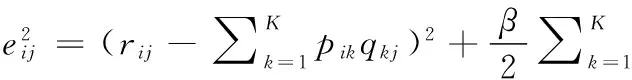
(3)

其中β是正则参数。最后的目标，就是每一个非缺失值元素的损失函数的总和最小。

为了快速有效地得到损失函数的最小值，需要对损失函数的更新采用优化算法。下面式(4)为基于梯度下降的优化算法，式(5)是P、Q矩阵里面每个元素的更新方式：

(4)

(5)

其中，θ、β均为优化参数。

对于类似播放频次这种隐式数据，加权矩阵分解会在大部分的隐式数据上工作得很好，因为它把所有的未投放位置都作为负样本，并给它们赋了一个更小的权重[8,9]。在加权矩阵分解中，对损失函数的每一项进行了加权修改：

(6)

其中wij为权重矩阵W第i行j列的元素，wij元素的值如下：

(7)

其中α(cij)为R矩阵每个元素的值，这表明权重是依赖于访问频率的。这样的设置可以体现访问频率是用户偏好的置信值的特性。

1.2基于数字标牌广告投放的兴趣点推荐模型

本文所采用的兴趣点推荐算法原理主要如图1兴趣点推荐算法原理所示，每个数字标牌实体即为一个兴趣点。首先构造出广告在兴趣点上的播放频次矩阵，然后通过矩阵分解算法将该矩阵分成两个隐式特征和对应兴趣点和广告组成的隐式空间，再通过附加上广告播放范围矩阵和兴趣点影响力矩阵，最后合并两个矩阵，形成最后的推荐结果矩阵。这样则可为播放频次数据引入可能影响推荐效果的其他数据，从而提高推荐结果的可信度。

图1　兴趣点推荐算法原理

图1中，播放频次矩阵R的每一个元素rij(其中1≤i≤M，1≤j≤N)为广告类型xi对应在数兴趣点yj上的对于播放时间加权的播放频次，i的最大值数为广告类型数M，j的最大值为兴趣点的个数N。由此矩阵直接进行矩阵分解得到的两个隐式特征矩阵(分别为M行K列和K行N列)组成的隐式空间。根据矩阵分解及内积的性质，可以为这两个隐式特征矩阵附加上包含其他信息的矩阵。当附加广告播放范围矩阵X(M行L列)和兴趣点影响力矩阵Y(L行N列)时，可以有效表达广告类型对不同兴趣点的偏好，所以本文选取此两矩阵作为附加信息，根据这两个矩阵的信息，为兴趣点推荐提供更多的可信度。

广告类型分布范围矩阵是由一系列区域以及广告类型在这些区域上出现的可能性共同组成的。而兴趣点的影响范围矩阵是由兴趣点能影响到的区域以及兴趣点对它们的影响力值所组成的。对于兴趣点的影响范围，当假设区域是通过把目标地域划分成L个的均匀网格得到的，表示为L={g1,g2,…,gi}(其中1≤i≤l)。因此定义如下：

定义1广告分布区域，一类广告的分布区域是指有一系列的广告可能会出现的网格区域gi(1≤i≤l)，在上面可能出现的非负的可能性x()i对所组成的。

本文可以把广告的分布区域表示成一个非负向量x={x1，x2，…，xi}(1≤i≤l)。其中每一个元素xl表示了此广告在网格区域gl出现的可能性。

定义2兴趣点的影响范围，即一个兴趣点的影响范围是由一系列的兴趣点能影响到的网格区域gl和在网格区域上的非负影响力yl对所组成的。

影响力的分布对于每个具体位置是连续并与周围位置有相互影响的，如图2影响力分布示例。

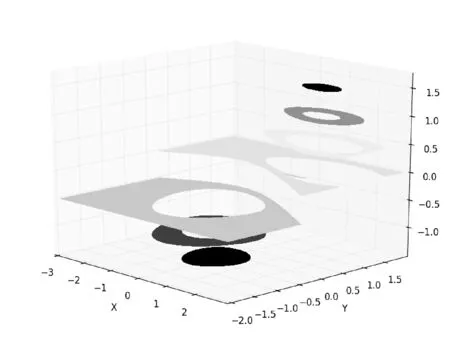
图2　影响力分布示例

X轴和Y轴分别表示地块的经度和维度的相对坐标，其中X轴坐标坐标由-3到2，Y轴坐标由-2到2，Z轴表示影响力的值。从图中可以看出某一具体位置的影响力。实际数字标牌影响力是没有负值的。此处为方便显示影响力的变化趋势引入负值。

同样，兴趣点影响范围区域也可以被转化成一个非负向量y={y1，y2，…，yi}(1≤i≤l)。当假设兴趣点的影响力是固定的且是以这个兴趣点为中心正态分布的。那么兴趣点i在网格区域gl的影响力如下：

(8)

其中K(·)为标准正态分布而σ则是标准差。d(l,i)表示兴趣点i与gl网格区域的距离。然而实际情况兴趣点的影响力往往是不同的，兴趣点的影响力受诸多因素影响，而其中一个可能影响最大的因素是社会经济因素，如人口、收入等因素。为此，本文希望通过对一些社会经济因素的分析，将兴趣点的影响力函数进行修正为：

(9)

其中ti为修正系数，直接决定于兴趣点所属网格区域gi的社会经济因素。为此，本文构建该修正系数矩阵：

(10)

其中ki,j表示第j个社会经济因素在i兴趣点所在地块区域上的取值，wj表示第j个社会经济因素的权重。各个权重的调整可根据不同网格区域所播放的广告时长总和比例及各个社会经济因素的比值进行调整。假设每个社会经济因素之间互不影响，将有广告播放记录的网格区域挑选出来，选取其中一个区域作为基准区域，以此区域各社会经济因素比例为基准设置初始权重。然后任意选取一个剩余区域，按广告播放时长比例与对应社会经济因素比例的比值逐步调整权重，进一步以更新后的权重为基准继续进行权重修正，直到所有有播放记录的区域迭代完即止。这样选取区域的好处在于每个区域所做的比较基本相同，因为目前还没法证明某个区域具有权重调整的代表性。第j个权重更新表达式为：

(11)

其中sn+1和sn分别表示后一次选择的区域的广告播放时长总和和前一次所选区域广告播放时长总和。

这样设置影响力向量的优点是x和y之间的点积对应了对广告类型投放位置的核密度估计。具体来说，广告类型u在兴趣点i上的估计密度等于：

(12)

其中Pu是广告类型u的投放兴趣点集合。如果这些兴趣点Pu被映射到相应的网格区域Lu⊆L，那么这个估计就变成：

(13)

其中nl为广告类型u对gl的投放频率。

本文利用x和y来扩展在矩阵分解中得到的广告类型隐向量和兴趣点隐向量。因此估计偏好矩阵，如下表示：

R=PQT+XYT

(14)

其中，所有广告类型的分布范围向量按行堆积得到广告类型分布范围矩阵X并且把所有兴趣点的影响范围向量按行堆积得到兴趣点影响区域矩阵Y。进行这种显式扩展来增加位置和商业信息的原因在于还没有证据说明隐式空间己经包含了位置和商业相关信息，这里可以看到很容易通过类似的方法添加其他类型的属性信息，比如兴趣点类别等。在这种情况下，广告类型对兴趣点的偏好就建模成扩展空间内的点积，因此包含了来自于隐空间的兴趣信息也包含了对兴趣点的位置偏好。如果广告类型对兴趣点的位置偏好是非零的，那么广告类型的分布区域是与兴趣点的影响范围相交的，从而，这些兴趣点是可以从广告类型的分布区域范围可达的。

最后需要对广告可达范围矩阵和兴趣点影响力矩阵进行调整：

(15)

其中，addsij为调整后的矩阵元素。k为调整系数，初始设为1，即视频次矩阵和附加信息矩阵对推荐结果影响作用相同。addij为调整前的矩阵i行j列元素。H1为频次矩阵中的最大值，L1为频次矩阵中的最小值。H2为附加矩阵中的最大值，L2为附加矩阵中的最小值。

2数据处理

本文广告播放数据及数字标牌关数据为合作企业提供，经济相关数据来源为第三次经济普查数据。其中播放记录为北京地区的1311块数字标牌在2013年1月至2014年12月间所产生的全部播放记录，约6GB大小数据量。并包括期间全部播放广告的基础数据，和数字标牌的基础数据。

2.1基础数据处理

2.1.1剔除冗余数据

播放记录中有无效播放记录或空播放记录，对之后的数据处理属于冗余信息，需要进行剔除。

2.1.2数据存储

需要将基础的数据存入数据库以备查询调用。包括基础的行业标签库，数字标牌(兴趣点)库，广告素材库，地块信息库。本文采用redis内存数据库进行存储。

2.1.3数据结果统计

对播放记录进行初步的统计并将统计结果存入对应数据库中。对统计数据入库。并形成广告类型和兴趣点的播放频次矩阵并存储成文件保存到本地。同时形成兴趣点和地块的影响力矩阵，此矩阵为根据经济因素调整后的矩阵，并存储成文件保存到本地。

2.2经济特征数据处理

本文所指的特征数据为那些可以反映某一地区完整经济情况并与地理位置有紧密联系的经济类型数据。对于这种经济特征数据的处理，首先需要去掉或合并关联度过大的经济数据。然后通过各地块的经济数据变化与播放时长记录变化的关联性分析，找出对播放时长影响进行特征提取。本文经过分析选取常住人口、商业从业人口和平均地价作为后续推荐结果的参考依据。

2.3地块数据处理

2.3.1地理数据分块

为方便统计地理位置上的经济数据，并与兴趣点产生关联。需要对地理位置进行分块，本文将兴趣点分布的范围分成500米×500米的小地块。地块有其中心点经纬度坐标。

2.3.2相关数据关联

在将地理数据分块好后，需要将各类经济数据关联到地块上，并根据地块坐标及所占范围将各数字标牌(兴趣点)与地块进行关联。将各数字标牌播放广告的有效时长总和统计结果关联到地块上。

3实验

3.1开发环境

本文采用python2.7作为开发语言。为快速响应查询信息，数据库选为Redis2.6。采用NumPy1.8.1进行数据处理。同时调用用于协同过滤的矩阵分解基础推荐算法LIBMF1.2库[10]进行基本矩阵分解。本文采用Matplotlib1.4.3进行数据的统计分析展示，采用ArcMap10.1对推荐结果关联到地理位置上的分析展示。

3.2推荐结果分析

最终推荐结果为广告播放频次矩阵分解的结果与数字标牌影响力矩阵和广告播放范围矩阵合并的结果。最终会为每个广告类型生成推荐数字标牌的列表。根据列表中值的大小决定为该广告类型推荐的数字标牌，也就是选取TopN结果推荐。

为了测试推荐结果的准确性，本文选用准确率(Precision)参数进行评定，其定义为pu=nu/Nu，其中pu为广告类型u的准确率，Nu为广告类型u选取N个推荐结果，nu表示这些推荐结果中为u实际播放过的个数。

为每种广告类型的前10个推荐结果进行Precision评定。图3为在广告类型中随机抽取的10种广告类型的Precision结果。

图3　随机抽取推荐结果Precision值

可以从图中看出推荐结果的Precision评定基本在10%左右，初步确定推荐结果具有一定的可信度。

图4展示了所有广告类型在北京范围内产生的前10个推荐结果中的Precision值的统计结果。

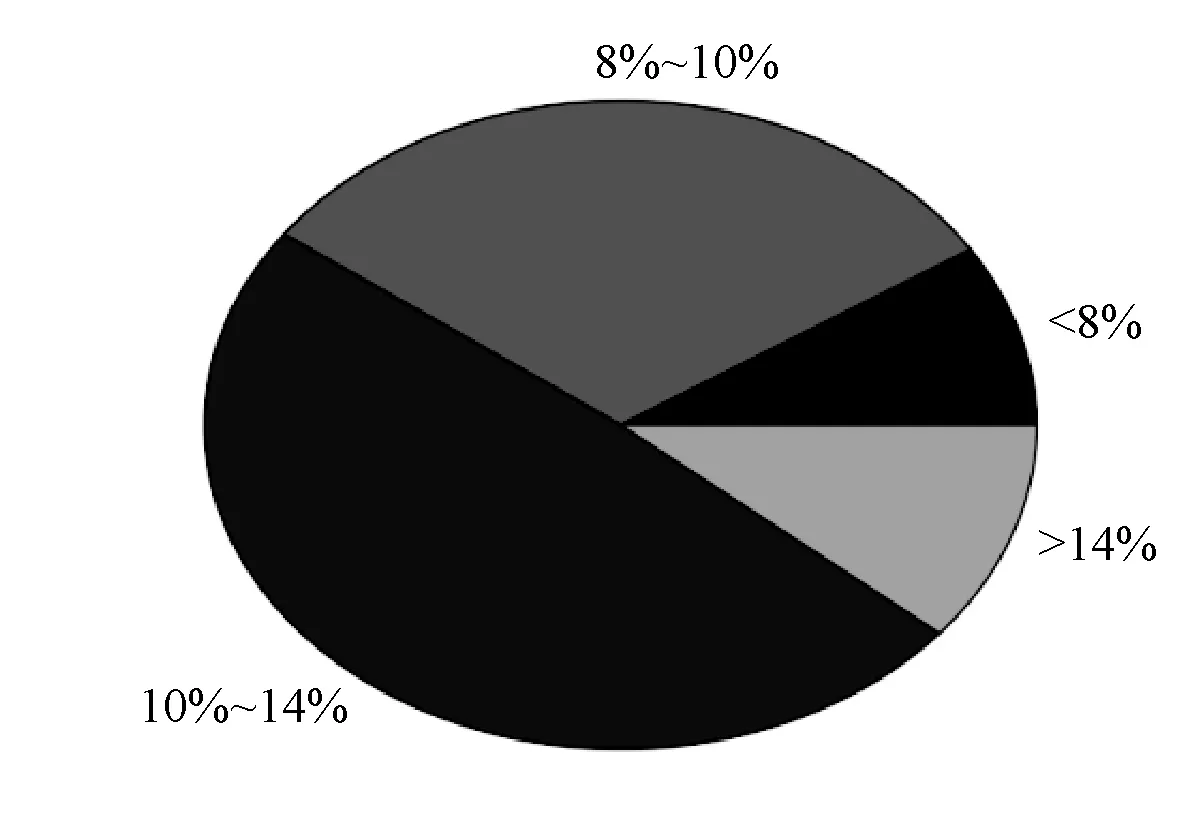
图4　广告类型Precision值统计

图4中的百分数，如10%～14%表示的是广告类型的Precision值在10%～14%之间，其所占的饼状图面积与整个饼状图的比值代表了Precision值在10%～14%之间的所有广告类型数占总的广告类型数的比值。从图中可以看出有超过75%的广告类型的Precision值集中在8%～14%概率上，这表明推荐结果在整体数据的推荐效果上是比较集中的。并且推荐结果在保持一定的可信度的同时，还拥有着不错的兴趣偏移预测，即因为时间、地点等因素改变所引起的播放兴趣转变。

对于某一类广告投放推荐结果，我们希望它能根据相似或相同类型广告的历史播放记录和商业地理信息数据，选出那些包含着投放用户已有投放经验，如在学校附近投放培训、教育类的广告，的数字标牌(推荐结果)。并且能根据商业地理信息数据为其筛选排序。以下为某一类广告推荐结果的具体分析。

商业地理信息数据就是将商业特征和现象的数值表征联系到它所在的地理信息上[11]。本文利用商业地理信息数据完成推荐结果在位置上的展示，展示选取技能培训、教育辅助及其他教育行业，行业代码为P829的广告的所有推荐结果展示在北京市范围内的分布情况。如图5为北京地区推荐结果分布。

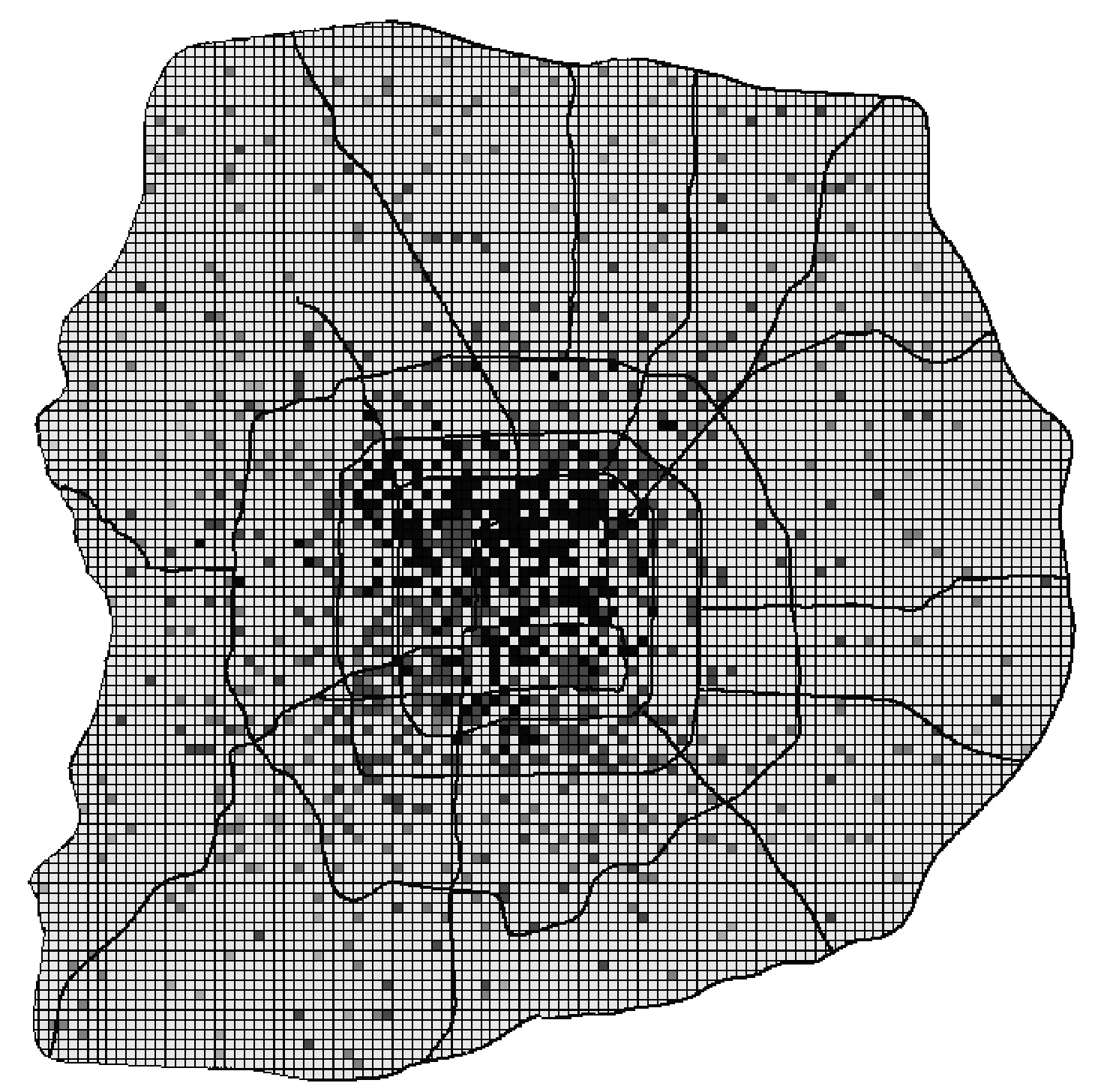
图5　P829北京地区推荐结果分布

途中颜色越深的点表示此位置的数字标牌的推荐值越高，颜色越浅的点表示推荐的值越低。可以看出大部分的高推荐度的数字标牌都集中在三环内。

为了更准确地看出推荐数字标牌分布的趋势，本文用相同的数据绘制了如图6北京地区推荐结果热度的推荐值的热点图。

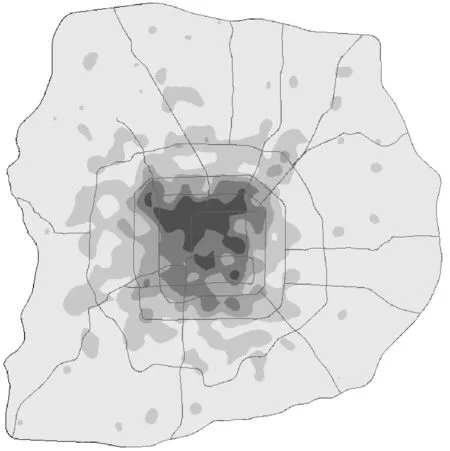
图6　P829北京地区推荐结果热度

图6中颜色越深的区域表示推荐的值越高，颜色越浅的区域表示推荐值越低。由图6中可以看出，对于技能培训类的广告，这里会推荐三环内偏北值的数字标牌进行投放，这些推荐结

果里包含着如“在学校附近投放培训教育类广告”等的投放经验，同时推荐值的排序也借助了商业地理信息的指导，那些人流密集，商业发达的地区的推荐值会更高，与推荐决策吻合。

4结语

本文通过基本的矩阵分解算法，利用它对其他数据的很好的扩展性能选取了部分商业地理信息融合在推荐算法中，从而在解决了数据稀疏性问题的同时为推荐结果提供了更多的推荐依据，提高了推荐结果的可信度。同时为数字标牌这种有着明显地理特征的兴趣点提供了一种可能的推荐模型。从推荐结果上看，本文在保证一定可信度的同时，为可能的兴趣偏移提供了一定的预测性能。

参考文献

[1] 丛秋波.数字标牌:新媒体,新趋势,新市场[J].电子设计技术,2009(6):76.

[2] 王敏,寇亚龙,赵霞.数字标牌广告即时排期优化算法研究[J].电脑知识与技术,2014(26):210-213.

[3] Ye M,Yin P,Lee W C,et al.Exploiting geographical influence for collaborative point-of-interest recommendation[C]//Proceedings of the 34th international ACM SIGIR conference on Research and development in Information Retrieval.ACM,2011:325-334.

[4] Cheng C,Yang H,King I,et al.Fused matrix factorization with geographical and social influence in location-based social networks[C]//Twenty-Sixth AAAI Conference on Artificial Intelligence,2012.

[5] Liu B,Fu Y,Yao Z,et al.Learning geographical preferences for point-of-interest recommendation[C]//Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining.ACM,2013:1043-1051.

[6] Zhang J D,Chow C Y.iGSLR:personalized geo-social location recommendation:a kernel density estimation approach[C]//Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems.ACM,2013:334-343.

[7] Lian D,Zhao C,Xie X,et al.GeoMF:joint geographical modeling and matrix factorization for point-of-interest recommendation[C]//Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining.ACM,2014:831-840.

[8] Hu Y,Koren Y,Volinsky C.Collaborative filtering for implicit feedback datasets[C]//Data Mining,2008.ICDM’08.Eighth IEEE International Conference on.IEEE,2008:263-272.

[9] Pan R,Zhou Y,Cao B,et al.One-class collaborative filtering[C]//Data Mining,2008.ICDM’08.Eighth IEEE International Conference on.IEEE,2008:502-511.

[10] Zhuang Y,Chin W S,Juan Y C,et al.A fast parallel SGD for matrix factorization in shared memory systems[C]//Proceedings of the 7th ACM conference on Recommender systems.ACM,2013:249-256.

[11] Zhang X,Zhang X,Zhong E,et al.Multi-Scale Centrality Measures of Street Network in Beijing,China[J].Sensor Letters,2014,12(3-5):651-658.

收稿日期：2015-07-02。国家自然科学青年基金项目(612020 60)；教育部人文社会科学研究青年基金项目(15YJCZp24)；北京市自然科学基金重点项目B类(KZ201410011014)；北京市教育委员会2015年度科技计划面上项目(KM201510011009)；北京市自然科学基金青年项目(9164025)。解贵龙，硕士生，主研领域：机器学习，数据挖掘。张珣，讲师。于重重，教授。赵霞，副教授。

中图分类号TP301.6

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.056

RESEARCH ON POI RECOMMENDATION ALGORITHM BASED ON DIGITAL SIGNAGE ADVERTISEMENT DATA

Xie GuilongZhang Xun*Yu ChongchongZhao Xia

(CollegeofComputerandInformationEngineering,BeijingTechnologyandBusinessUniversity,Beijing100048,China)

AbstractTo solve the problem of digital signage advertising recommendation, we studied the location data-based recommendation algorithm. On the basis of existing point of interest (POI) recommendation algorithm, which is based on matrix factorisation idea, we proposed a POI recommendation model which combines the matrix factorisation idea and commercial GIS data, and conducted experiments on location-based digital signage advertising data. Experimental results showed that, by the method appending commercial GIS data to matrix factorisation, the problem of location access data sparseness has been solved, and this provides an effective reference and implementation approach for the problems of single data type and insufficient recommendation basis. Our study provides an important reference basis for the digital signage advertising.

KeywordsPoints of interest recommendationDigital signageLocation recommendationMatrix factorisation