一种强鲁棒性自适应活性边表算法

师　硕　姚陈堃　于　洋

(河北工业大学计算机科学与软件学院　天津 300401)



一种强鲁棒性自适应活性边表算法

师硕姚陈堃于洋

(河北工业大学计算机科学与软件学院天津 300401)

摘要为提升多边形的填充效率，在分析和比较常见填充算法后，以活性边表算法为基础，深入挖掘不同扫描方向上的求交次数及多边形自交特性，提出一种强鲁棒性自适应活性边表算法。新算法引入横度和纵度的概念表示横纵扫描方向上的求交次数，并以此为标准自适应选择扫描方向。此外，通过对活性边表中相邻交点的横坐标进行检测和纠正，正确而高效地填充了自交多边形。经实验验证，新算法灵活的自适应性和高效的自交纠正方法，大大提高了时间效率和鲁棒性。

关键词多边形填充自适应扫描活性边表算法自相交鲁棒性

0引言

区域填充被广泛应用于真实感图形显示、图像处理、机械制造和媒体广告等领域[1,2]，尤其是近年来移动设备上富媒体应用的增多，对图形填充算法的时空方面提出了更高的要求[3]。

常用的区域填充算法有逐点判断算法、种子填充算法和扫描线填充算法[4,5]。逐点判断算法基于像素，对绘图窗口内每一像素点进行射线环绕探测来实现内点判定，孤立地考虑像素点与区域间的关系，计算量较大[5]；种子填充算法需事先给定一像素点作为种子点，再以该种子点为起点朝四连通或八连通方向递归填充，但仍基于像素，且区域内每一像素点均需入栈，易堆栈溢出[1,5]；扫描线填充算法也需给定一种子点，分别水平向右和向左地探测得到图形边界点，填充两端点之间的线段，并让该线段之上和之下的任意内点入栈，继而栈顶像素点出栈作为新的种子点，重复上述操作至栈空[6]。不难看出，扫描线填充算法中种子点入栈次数与扫描线条数相同，较种子填充算法大大减少了堆栈操作，时空开销均有降低。

但随着区域面积的增大，扫描线填充算法的出、入栈操作仍很频繁[4]。活性边表算法，又称有效边表算法或多边形填充算法，它充分挖掘了边的连贯性和顶点间的约束关系，从而有效避免了复杂的计算和耗时的堆栈操作[7,8]。目前已有学者对该算法进行了改进，如文献[9]中杨长强等人提出了一种用水平扫描线与B样条曲线求交的填充算法，文献[10]中Al-Rawi I提出了一种链表与数组结合并分凸、凹和复合多边形填充的算法等。

考虑到目前算法均单一方向地扫描多边形，并且无法正确填充自交多边形，本文提出一种能预判断最佳扫描方向并纠正多边形自交点的活性边表算法。

1传统的活性边表算法

传统的活性边表算法让扫描线以1像素的增量自下而上地扫描多边形，如图1所示，其中水平虚线为扫描线，空心圆点为扫描线与多边形的交点。euv=pupv为多边形的任一边，它的上端点纵坐标yv=ym，li与li+1(i=1,2,…,9)分别为当前扫描线和下一条扫描线，它们与euv的交点分别为(xi,yi)和(xi+1,yi+1)。dx为交点横坐标的增量，为得出dx的计算公式，不妨假设euv所在直线方程为ax+by+c=0，斜率为k，易知：

(1)

dx=xi+1-xi

(2)

将式(1)代入式(2)可得：

(3)

再由li和li+1的步进关系知：

yi+1-yi=1

(4)

将式(4)代入式(3)得：

(5)

填充前，需根据多边形构造新边表NET，图1中多边形的NET如图2所示。邻接表每行的表头结点代表一条扫描线，其后每个结点代表一条边，其中关于边结点的定义如下：

class Edge

{

double xi;

double dx;

intym;

Edge nextEdge;

}

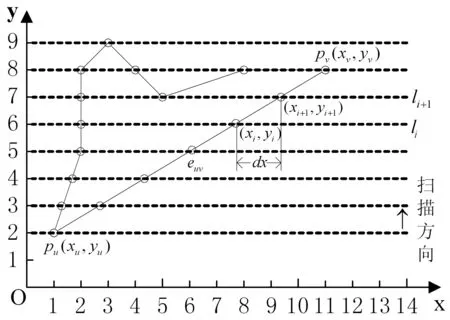
图1　扫描多边形的过程

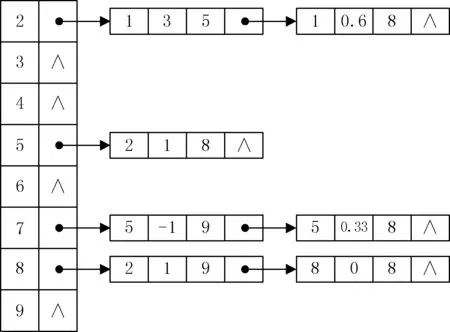
图2　NET的逻辑结构

另还需用活性边表AET记录当前扫描线与多边形的所有交点信息，图2中扫描线l6的AET如图3所示。

图3AET的逻辑结构

传统的活性边表算法的基本步骤如下：

Step1构造NET与AET。

Step2删除AET中ym和yi相等的所有边结点，将NET中扫描线所在行的所有边结点按xi升序插入AET。

Step3利用公式xi=xi+dx更新AET中各交点。

Step4对AET中交点两两配对，并填充其间的区域。

Step5扫描线步进。若扫描线与多边形有交点，则转Step2;若无交点，则结束。

2强鲁棒性自适应活性边表算法

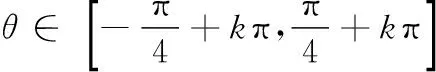
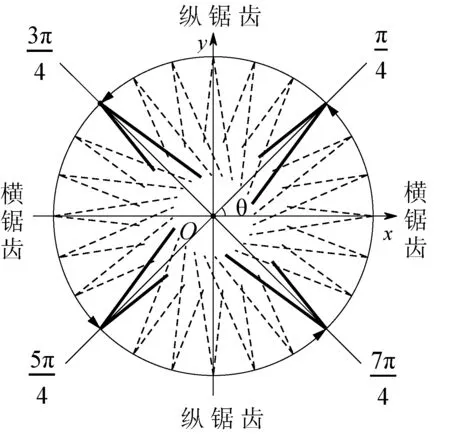
图4　横纵锯齿

定义2自下而上地扫描为纵向扫描，自左向右地扫描为横向扫描，如图5所示。

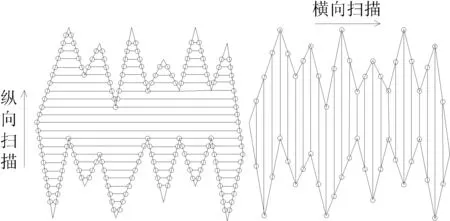
图5　横向与纵向扫描多边形的情况对比

分析发现，传统的活性边表算法存在如下缺陷：1) 扫描方向单一，仅考虑纵向扫描，而事实上纵向并非总是最佳方向，如图5所示的多边形，其内部纵锯齿居多，若选择纵向扫描，交点较多，计算量大，生成的配对区间也较多而小，直接导致填色次数与链表操作增多，而若选择横向扫描，则可一定程度地简化上述问题；2) 当输入为自交多边形时，将产生填充异常，算法的鲁棒性不强。

针对上述问题，本文提出一种强鲁棒性自适应活性边表算法。该算法在填充前先对多边形的形状进行预判断，自动调整扫描线的方向后再执行传统的活性边表算法，且在更新AET时，对相邻交点的xi进行升序纠正，正确填充了自交多边形。

2.1自适应性

2.1.1扫描方向的确定

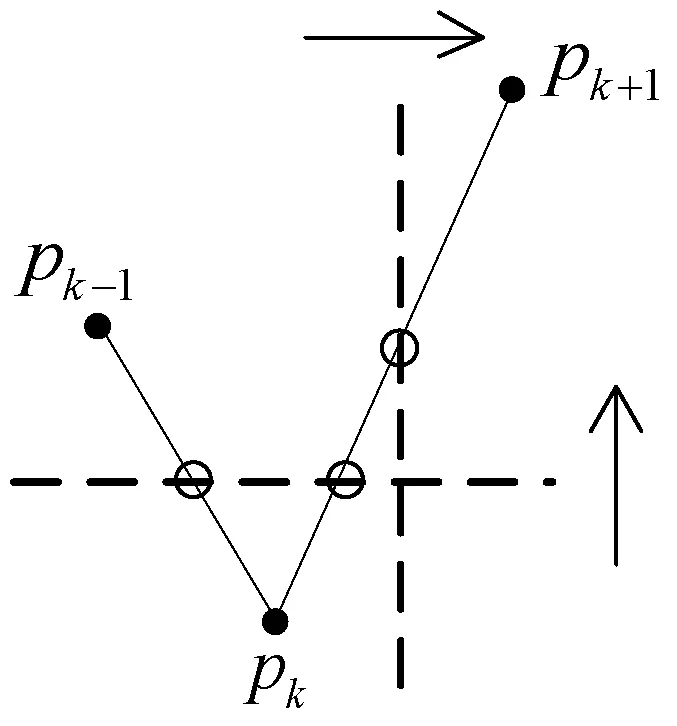
图6　锯齿与扫描线求交

扫描方向的确定依赖于快速、准确且低运算量的决策算法，本文通过分析扫描线与锯齿的求交过程，得出了求交次数的数学公式，并给出了决策算法的描述。

现任取一多边形的第k个锯齿，其顶点集为{pk-1,pk,pk+1}，如图6所示，分别横向和纵向地扫描该锯齿，易知线段pk-1pk与pkpk+1在扫描方向上的投影长度之和即为求交次数，如式(6)、式(7)所示：

(6)

(7)

将式(6)、式(7)推广到整个多边形后，得式(8)、式(9)：

(8)

(9)

从式(8)、式(9)的求和过程可知，多边形每条边的求交次数被重复计算了一次，而最终只需比较Tx和Ty的大小即可确定扫描方向，故可继续通过定义3化简。

定义3Dx和Dy为多边形的横度和纵度，它们分别表示横向和纵向扫描多边形的求交次数，也表征多边形形状在横纵方向上的复杂程度。

(10)

(11)

2.1.2决策算法的描述

下面，采用伪代码的形式给出决策算法的描述：

polygon:存储多边形顶点坐标的数组

N:多边形顶点数目

cur:当前顶点下标

rear:当前顶点的后继顶点下标

abs:取绝对值

for(cur=0; cur< N; cur++)

{

rear = (cur + 1) % N;

Dx+= abs(polygon[rear].x - polygon[cur].x);

Dy+= abs(polygon[rear].y - polygon[cur].y);

}

if(Dx>Dy)

纵向扫描活性边表算法;

else

横向扫描活性边表算法;

2.2自交纠正算法

传统算法在填充自交多边形时之所以产生异常，是因为相交的两条边在更新各自的xi到其排列次序变为降序后，并未采取措施以纠正为原来的升序。目前诸多算法采用在更新xi后加入起泡排序来解决，但这种方法孤立地考虑当前AET中所有交点的有序性，而未从自交点产生原因的角度分析，故而产生了许多不必要的比较和判断。

针对该问题，本文用一种简单的交换算法替换起泡排序算法，其基本思想是：遍历AET，若发现当前边结点与其后继边结点的xi成降序，即满足edge·xi>(edge·next)·xi，则交换它们的位置。

为对比新旧自交纠正算法的效率，不妨假设问题的规模为n，即当前AET中有n个边结点，其效率对比如表1所示。

表1　新旧自交纠正算法的时间效率对比

从时间复杂度看，交换算法较起泡排序算法降低了一个数量级；从比较次数看，当n=1或n=2时两种算法的比较次数相等，当n>2时交换算法的比较次数更少。综合看来，交换算法更具时间优势。

3实验分析

考虑到近年来移动设备的广泛普及，以及Android平台较高的市场占有率，本文基于Android平台，用Java语言编写了测试程序，并在4英寸、480×854分辨率、双核1.5 GHz和1.00 GB内存的小米手机上运行和测试。该部分选取了若干多边形作为测试用例，其属性数据如表2所示。共设计了三个实验，其中实验1用以比较常用填充算法与本文算法的时间效率，实验2用以比较纵向、横向和自适应方向扫描的活性边表算法的时间效率，实验3给出了剪纸图案和空心文字的实际填充效果。

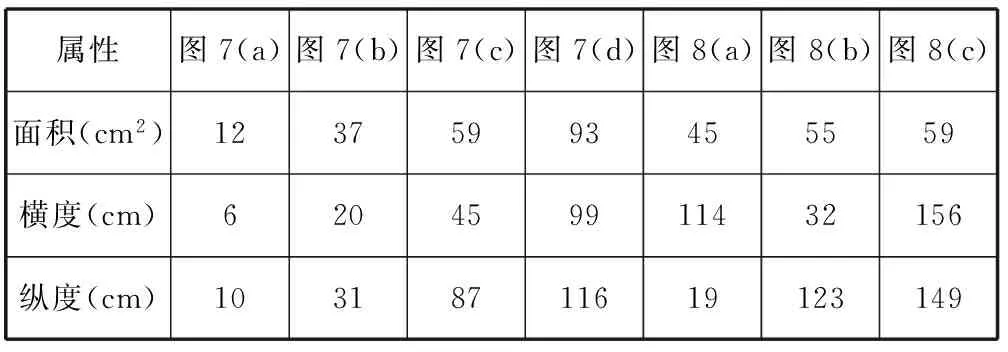
表2　实验用多边形的属性数据

实验1选取四个具有典型特征的多边形，每个多边形分别用逐点判断算法、种子填充算法、扫描线填充算法、传统的活性边表算法、自适应活性边表算法填充10 000次，并计算平均耗时，其填充效果如图7所示，时间效率统计如表3所示。

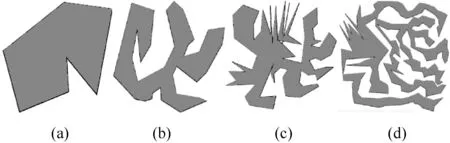
图7　实验1用多边形及填充效果

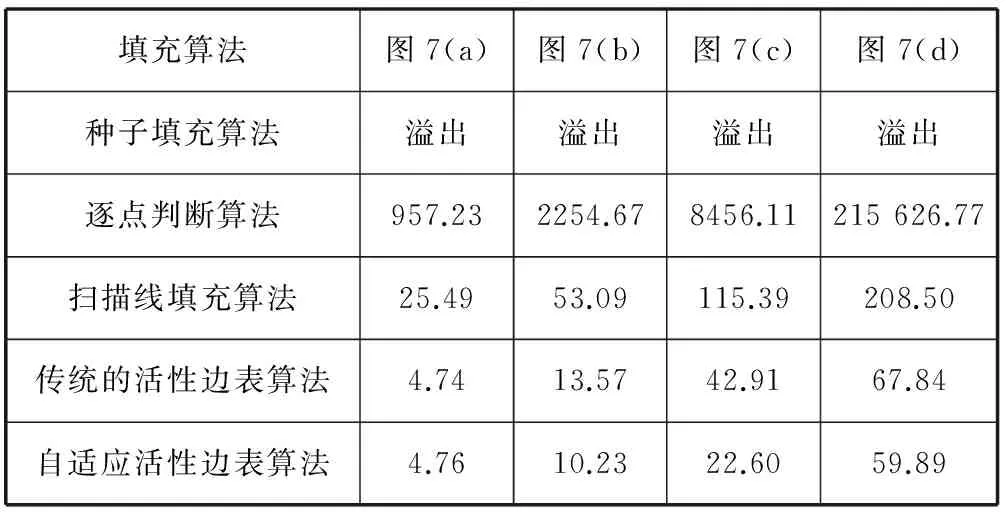
填充算法图7(a)图7(b)图7(c)图7(d)种子填充算法溢出溢出溢出溢出逐点判断算法957.232254.678456.11215626.77扫描线填充算法25.4953.09115.39208.50传统的活性边表算法4.7413.5742.9167.84自适应活性边表算法4.7610.2322.6059.89

深入分析表3，并对照表2可以发现：

1) 种子填充算法空间开销较大，不宜在内存紧缺的移动平台使用；逐点判断算法的时间效率较低。

2) 扫描线填充算法的时间效率受区域面积影响较大，而活性边表算法则相对稳定。

3) 自适应活性边表算法较传统的活性边表算法时间效率有所提高，且横纵度差距愈大愈明显。

实验2选取偏横度、偏纵度和横纵度相当的三个多边形，每个多边形分别用纵向、横向和自适应方向扫描的活性边表算法填充10 000次，并计算平均耗时。其中纵向和横向扫描的活性边表算法采用起泡排序算法进行自交纠正，而自适应活性边表算法采用交换算法，其填充效果如图8(a)、(b)、(c)所示，时间效率统计如表4所示，时间效率对比如图9所示。另为验证自交纠正与否对填充结果的影响，采用不含自交纠正的活性边表算法对图8(c)多边形填充，效果如图8(d)所示，可见产生填充异常。

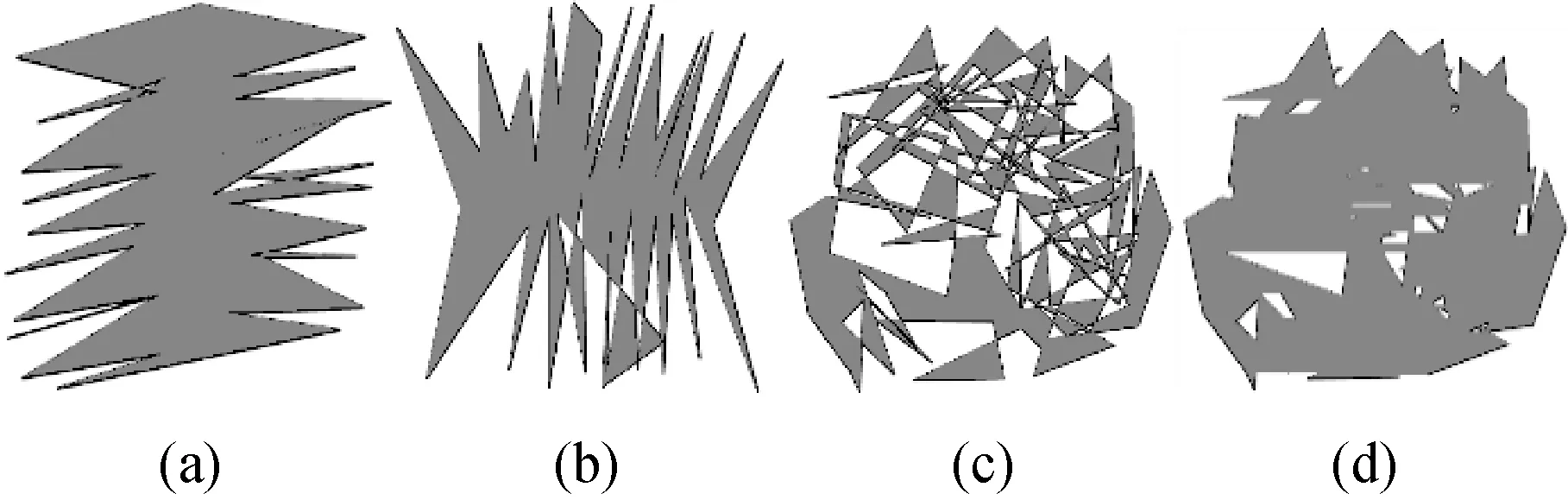
图8　实验2用多边形及填充效果

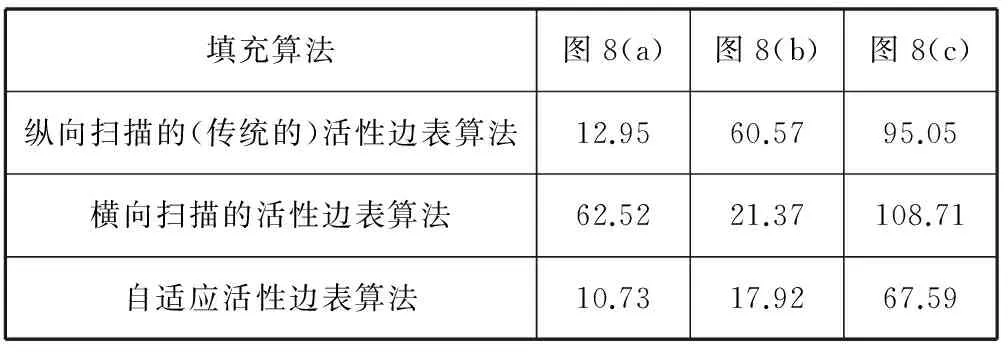
填充算法图8(a)图8(b)图8(c)纵向扫描的(传统的)活性边表算法12.9560.5795.05横向扫描的活性边表算法62.5221.37108.71自适应活性边表算法10.7317.9267.59

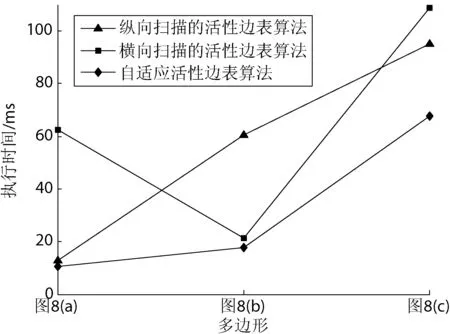
图9　三种扫描方式的时间效率对比

深入分析图9，并对照表2可以发现：

1) 自适应活性边表算法可自适应地找到耗时较少的扫描方向，验证了新算法自适应结果的正确性。

2) 自适应活性边表算法的耗时比其余两种算法中耗时较少者还少，尤以图8(c)最明显，证明交换算法较起泡排序算法更能加快自交多边形的填充速率，且自交程度愈复杂愈明显。

实验3采用本文的自适应活性边表算法填充剪纸图案和空心文字，效果如图10和图11所示。需要指出的两点是：1) 任意形状的轮廓线均可由若干距离较短的线段构成，进而任意形状的图形也可用近似的多边形代替[11]；2) 活性边表算法的适用范围可推广至含有若干孔洞的连通区域，此时只需将区域分为内、外多边形，并为其分别构造NET即可[12]。

图10　剪纸图案及填充效果

图11　空心文字及填充效果

4结语

区域填充是计算机图形学中的重要问题，在诸多领域也有着广泛的应用，其中活性边表算法最常用也最可观。然而传统的活性边表算法固定了扫描方向，未根据多边形的形状对扫描方向做出自适应地调整，对于自交多边形的特殊情况，也未深入挖掘其特性，造成了冗余的操作。本文从扫描线与多边形的求交次数进行分析，引入横度和纵度来分别表征横向和纵向扫描时的求交次数。通过比较它们的大小选择最佳的扫描方向，达到自适应的效果。后又采用交换算法纠正自交点，确保了正确而高效的填充。经理论和实验分析可见，本文算法简单易行，灵活智能，且填充效率也有较大提升。

参考文献

[1] 徐胜攀,刘正军,左志权,等.一种改进的活性边表区域填充算法[J].计算机工程与应用,2014,50(17):178-181.

[2] 唐永勇,冯剑,杜振华,等.基于顶点的多边形扫描转换[J].计算机与现代化,2011(1):117-120.

[3] 张骥先,罗蕾,姜帆.移动设备上富媒体场景渲染优化策略[J].计算机辅助设计与图形学学报,2010,22(8):1272-1278.

[4] 孙家广,杨长贵.计算机图形学[M].3版.北京:清华大学出版社,2002:170-205.

[5] 吴力心,申闫春.区域填充算法的研究与应用[J].计算机应用与软件,1994(2):31-37.

[6] 张荣国,刘焜.新区入栈的区域填充扫描线算法[J].计算机工程,2006,32(6):63-64.

[7] Gordon D,Peterson M A,Reynolds R A.Fast polygon scan conversion with medical applications[J].Computer Graphics and Applications,IEEE,1994,14(6):20-27.

[8] 陈万领,黄培,陈卓宁,等.一种新的任意多边形的快速填充算法[J].计算机应用与软件,1999(4):23-26.

[9] 杨长强,彭延军,郑永果.一种封闭B样条曲线的扫描线填充算法[J].系统仿真学报,2006,18(S1):12-13.

[10] AlRawi I.Implementation of an Efficient Scan-Line Polygon Fill Algorithm[J].Computer Engineering and Intelligent Systems,2014,5(4):22-28.

[11] 周天娟,张铁中,杨丽.草莓采摘机器人的研究:Ⅲ.扫描线填充算法在草莓图像孔洞填充中的应用[J].中国农业大学学报,2007,12(2):67-71.

[12] 张志龙,李吉成,沈振康.一种新的快速复杂连通区域扫描线填充算法[J].计算机工程与应用,2004(31):6-8.

收稿日期：2015-02-03。天津市科技计划项目(14RCGFGX008 46)；河北省教育厅高等学校科学研究计划项目(Z2013078)。师硕，讲师，主研领域：图像特征提取，图形图像处理，网络编程。姚陈堃，本科生。于洋，讲师。

中图分类号TP301.6

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.049

AN ACTIVE-EDGE-TABLE FILLING ALGORITHM WITH ADAPTABILITY AND ROBUSTNESS

Shi ShuoYao ChenkunYu Yang

(SchoolofComputerScienceandEngineering,HebeiUniversityofTechnology,Tianjin300401,China)

AbstractTo improve the efficiency of polygon filling, after analysing and comparing several common filling algorithms, the paper puts forward an active-edge-table filling algorithm with adaptability and robustness, which is based on active-edge-table algorithm, by thoroughly mining the number of crossover requests in different scanning directions and the self-intersection character of polygon. The new algorithm introduces the concept of horizontal extent and vertical extent to represent the number of crossover requests in horizontal and vertical directions of scanning, and takes them as the standard to adaptively choose the right scanning direction. In addition, by checking and correcting the coordinates of the adjoining crossover points in active-edge-table, this algorithm fills the self-intersected polygon correctly and efficiently. It is verified by experiment that the new algorithm greatly improves the time efficiency and robustness owing to its flexible adaptability and efficient self-intersection correcting way.

KeywordsPolygon fillingAdaptability scanActive-edge-table algorithmSelf-intersectionRobustness