利用空间抽样理论的遥感影像分类结果精度评价方法

黄冬梅　陈　珂　王振华　刘　爽

(上海海洋大学信息学院　上海 201306)



利用空间抽样理论的遥感影像分类结果精度评价方法

黄冬梅陈珂王振华刘爽

(上海海洋大学信息学院上海 201306)

摘要遥感影像分类结果的准确性对于遥感信息的应用分析有着重要的影响。传统抽样方式下的遥感影像分类结果精度评价方法受样本量及空间布局的影响，存在效率低和信息冗余等问题。利用空间数据的相关性，将空间抽样理论应用于遥感影像分类结果的精度评价，通过与传统抽样方法比较，发现空间抽样方法应用于遥感影像分类结果的精度评价不仅降低了数据冗余，同时提高了精度评价的检验效率和准确性。

关键词遥感分类精度评价抽样理论误差矩阵

0引言

随着遥感技术的发展，遥感影像分类作为遥感影像处理及信息处理的重要组成部分在土地利用制图、变化监测及专题制图等[1]领域有着广泛的应用，其结果的准确性和可靠性对信息的处理和分析有着重要的影响，因此，遥感影像分类结果的精度评价和分析是进行科学决策的前提和重要保障。抽样理论作为遥感影像分类结果精度评价过程中的重要环节之一，已经被国内外学者广泛应用在土地资源监测[2]、种植面积估算、自然灾害预测等[3]精度评价的多个领域。传统抽样的遥感影像分类结果精度评价方法,一般采用基于概率理论的抽样方法选取样本,通过对样本区域进行实地调查和取样,从而对遥感影像的分类结果进行精度评估和分析[4]，典型的方法主要有:简单随机抽样、分层随机抽样、系统抽样和整群抽样等。传统抽样的遥感影像分类结果精度评价方法受样本量的大小、样本点的空间分布的影响，同时，空间对象具有空间相关性，而基于概率论的传统抽样方法在样本的确定及空间布样方面具有随机性，因此，传统抽样的精度评价方法不适用遥感数据的精度评价和分析。此外，传统抽样方式下的遥感影像分类结果精度评价方法依靠观察者的主观感觉[5,6]，精度评价结果缺乏客观性。随着遥感技术的发展，数据的获取快速增长，基于传统抽样理论的遥感影像分类精度评价方法不适应海量遥感数据处理与应用的需要，因此需要研究新的遥感影像分类精度评价方法。

空间抽样理论顾及空间对象之间的相关性和变异性，因此在地学研究中得到了迅速发展，已经广泛应用于地理研究、资源评估和农作物监测等[7,8]各个领域。Matheron[9]最早提出了Kriging方法，将其应用与地质矿产的研究中；李连发[10]等人考虑了空间数据的相关性，并利用量化相关性的方法，提出了空间抽样框架，提高了抽样的效率；王劲峰[11]等人以分层抽样为基础，并且考虑了空间关联性，提出“三明治”空间抽样模型；王振华[12]等人将模糊集理论与抽样检验理论相结合，提出了基于空间数据质量检验的二级抽样模型。

为了分析传统抽样的遥感影像分类结果精度评价方法的局限性，本文首先针对遥感影像分类结果的特点，采用传统抽样的遥感影像精度评价方法对遥感影像的分类结果进行评价。然后考虑空间数据之间的空间相关性，采用Moran指数对传统抽样理论中样本量的确定方法进行优化。最后，对传统抽样理论和空间抽样理论获取的遥感影像分类结果的精度评价结果进行对比和分析。

1研究方法

传统抽样的遥感影像分类结果的精度评价方法[13],一般是基于概率论选取样本,通过对样本区域进行实地的调查和取样,从而对遥感影像的分类结果进行精度评估和分析。但是，传统抽样理论是基于抽样随机性的统计推断，忽略了空间对象之间的空间相关性，因此在样本量的确定方面具有很大的局限性。Moran指数是一种度量空间对象之间相关程度的重要参数，在空间自相关分析中得到了广泛的应用。因此，本文首先采用简单随机抽样方法、系统抽样方法、传统分层抽样方法进行样本量的确定与空间布样，随后采用Moran指数对传统的样本量确定方法进行优化，并结合高分辨率的遥感影像对遥感分类结果进行精度评价，最后，对传统抽样方法精度评价与空间抽样方法精度评价结果进行对比分析，以期得到更合适的遥感影像分类结果的精度评价方法。本文的数据处理基本流程如图1所示。

图1　遥感影像分类结果评定流程图

1.1传统抽样方法

样本量的确定和样本的空间布样对遥感影像分类精度评价结果具有重要的影响，传统抽样理论主要基于概率论的方法确定样本量，当样本总体较大时，可以通过控制不合格品率样本估值与真值之间的最大相对误差方法确定抽样所需的样本量[12]：

(1)

传统抽样方法主要有简单随机抽样方法、系统抽样方法、分层抽样方法。简单随机抽样方法是指从一个单元总数为N中逐个抽取单元并且无放回，每次都在所有尚未进入样本的单元中等概率地随机抽取，直到n个单元被抽中。系统抽样方法是指对研究总体按一定的顺序排列，每隔一定的间隔抽取一个单元的抽样方法。分层抽样方法是按照等比分层抽样在各层中随机抽取样本的抽样方法。

由于空间对象之间存在空间相关性，因此空间事物在分布上呈现空间结构性。但传统抽样方法基于概率理论，在对空间对象进行调查时，忽略了样本的空间分布，从而导致样本的冗余和不足。空间抽样方法考虑了调查对象的空间结构性，因此可以合理地选取具有代表性的样本，减少样本冗余，降低检验成本。

1.2空间抽样方法

空间自相关是空间地理数据的重要性质，空间中邻近的地理数据信息通常比相离较远的地理数据信息具有较高的相似性。空间自相关性分析是空间抽样的前提，Moran’s I是一种通用的空间自相关测量方法,在各个领域的空间自相关分析中广泛使用。Moran’s I的公式[14]为：

(2)

其中，xi为单元i的属性值，n为单元的总数，Wij为i和j之间位置的接近性，Sij为单元i和j之间属性的相似性，它是根据各点的属性值和所研究的单元的所有属性值均值之间的差异来定义，σ2为总体的方差。

抽样方法选择的样本只有在空间自相关显著的前提下，才有空间自相关性。在计算出空间自相关的量化指标Moran’s I后，需要检验空间自相关显著性，检验步骤为：

1) 在随机假设条件下，计算Moran’s I的期望值和方差；

2) 计算出标准化Z值；

(3)

其中，E(I)表示Moran’s I的期望，V(I)表示Moran’s I的方差。

3) 比较Z值显著性水平的临界值，若Z值大于显著性水平的临界值时，样本单元的空间自相关性显著，反之，不显著。

4) 在样本单元的空间自相关性显著的前提下，计算空间抽样方法的样本量。

在传统抽样中，样本量通常由总体方差、均值方差、期望等数据计算而得，其中由总体方差σ2与均值方差v之比确定样本量的方法比较常见，即：

(4)

在空间抽样理论中，均值估计方法需要根据空间抽样对象的相关程度而调整。因此，均值方差为：

(5)

(6)

1.3遥感影像分类结果精度评价模型

(1) 基于误差矩阵的遥感影像分类结果精度评价模型

误差矩阵用于遥感影像分类结果和真实土地类型信息的比较，参考指标有用户精度、总体精度、Kappa系数等。用户精度为每类像元被正确分类的精度，由该类土地类型中正确分类的像元数与该类土地类型总像元数之比获得；总体精度为总体像元被正确分类的精度，由各类土地类型中被正确分类的像元总和与总像元数之比获得。Kappa系数是在综合了用户精度和总体精度两个参数上提出的一个最终指标，Kappa系数越高说明分类结果精度越高。

(7)

式中K是Kappa系数，r是误差矩阵的行数，xii是行列(主对角线)上的像元的数量，xi+和x+i分别是第i行的和与第i列的和，n′是样本点总数。

(2) 基于误差矩阵的精度评价算法

基于误差矩阵的精度评价算法如下：

INPUT:样本点总数n′，误差矩阵的行数r；

OUTPUT:误差矩阵的Kappa系数K。

① 初始化:令误差矩阵的行数i=1，对应x1+和x+1分别是第1行的和与第1列的和。

② for(i=1;i<=r;i++){利用式(7)计算出主对角线上值的和}。

③ for(i=1;i<=r;i++){利用式(7)计算出xi+x+i的和}。

④ 输出误差矩阵的Kappa系数K。

算法分析:

在该算法中，① 在样本点为n′，误差矩阵行数为r情况下，求遥感影像分类结果的Kappa系数的时间复杂度为O(r);② 由分析可知，基于误差矩阵的精度评价算法的时间复杂度与误差矩阵的行列数有关，与样本点的总数无关，当样本量n′足够大时，基于误差矩阵的遥感影像分类结果精度评价方法具有较明显优势。

2结果分析与讨论

2.1实验区域与数据

为了研究传统抽样理论与空间抽样理论对遥感影像分类结果精度评价的效果，本研究将Landsat-8中截取的上海某地区200×200像元的30m 分辨率遥感数据用于遥感影像的分类，投影类型为Transverse Mercator，坐标系统为WGS-84, 如图2(a)；同时，采用同一地区分辨率为3m的高分辨率遥感数据用于分类结果的精度评价，如图2(b)。选取该区域主要有两个原因：第一，该区域土地利用类型丰富，研究结果有较好的代表性；第二，区域位置方便实地考察，便于求得较为准确的土地信息。

图2　Landsat-8低分辨率遥感影像及高分辨率遥感影像

在获取遥感影像的过程中，由于受遥感平台位置、运动状态、地形起伏、地球表面曲率以及大气折射等因素的影响，产生影像行列不均匀、像元大小与地面大小对应不准确、地物形状不规则变化等畸变。因此，本研究在ENVI 4.7软件的支持下，对30 m分辨率与3 m分辨率的遥感影像进行几何纠正和配准等影像处理，采用极大似然遥感影像分类算法，对30 m分辨率的Landsat-8遥感影像进行遥感影像分类处理，将研究区域的土地利用类型分为土地、建筑、水域和道路4种土地利用类型，如图3所示。

图3　Landsat-8低分辨率遥感影像分类结果

极大似然遥感影像分类算法是经常使用的分类方法之一，它是通过求出每个像元对于各类别归属概率，把该像元分到归属概率最大的类别中去的方法。

极大似然遥感影像分类算法在多类别分类时，常采用统计学方法建立起一个判别函数集，然后根据这个判别函数集计算各待分像元的归属概率。这里，归属概率是指：对于待分像元x，它从属于分类类别k的概率。

设从类别k中观测到x的条件概率为P(x|k)，则归属概率Lk可表示为如下形式的判别函数：

Lk=P(k|x)=P(k)×P(x|k)/∑P(i)×P(x|i)

(8)

式中，x为待分像元，P(k)为类别k的先验概率。

2.2结果分析与讨论

为了对遥感影像的分类结果进行精度评价，本文首先根据传统样本量的确定方法获得实验所需的样本总数，然后分别采用简单随机抽样、系统抽样及传统分层抽样方法对样本点进行空间布样，最后以3 m高分辨率遥感影像作为参考影像，采用基于误差矩阵的遥感影像精度评价方法对遥感影像的分类结果进行精度评价与分析讨论。

(1) 样本量的确定与空间布样

本文对遥感影像分类结果进行精度评价的过程中，首先根据影像的像元总数，确定精度评估所需的样本量，其中样本总量为40 000像元，在置信水平为90%，质量水平为0.02，最大允许相对误差为0.1时，可以获取样本量为2650像元，分别采用简单随机抽样，系统抽样及分层抽样对样本点进行空间布样。在简单随机抽样中样本点按照简单随机抽样模型，随机分布在分类图上，如图4所示；在系统抽样中，采用等间隔的系统抽样方法获取样本，如图5所示；在分层抽样中，各层样本量的采用比例分配，每层的样本量与层的大小成比例，由此，获取的土地层、建筑层、水域层、道路层的样本量分别为1313、465、315、557，样本点采用等比分层抽样方法在各层中随机抽取，如图6所示。

图4　随机抽样样本点的空间分布

图5　系统抽样样本点的空间分布

图6　传统分层抽样中各层样本点的空间分布

(2) 分类结果精度评价与分析

基于误差矩阵对抽样结果进行精度评价的方法是目前比较常见的遥感影像分类结果精度评价方法。实验将简单随机抽样、系统抽样、分层抽样三种传统的抽样方法分别与基于误差矩阵的精度评价方法相结合，采用高分辨率遥感影像的真实土地利用类型对遥感影像的分类结果进行精度评价和分析，结果如表1-表3所示。

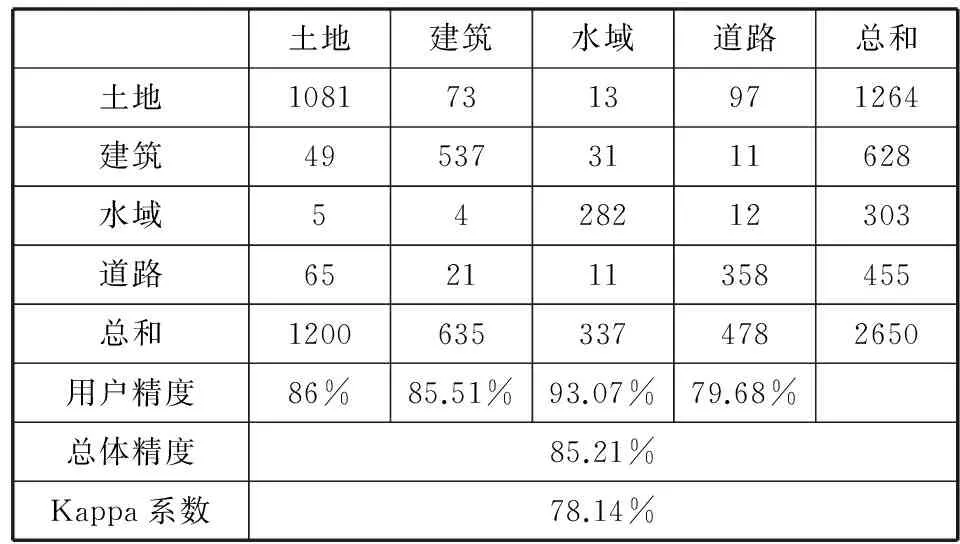
表1　简单随机抽样方法的遥感影像分类结果精度评价

由表1看出，简单随机抽样获取的遥感影像的分类结果的分类总体精度为85.21%，Kappa系数为78.14%，其中在土地、建筑、水域、道路四种土地类型的精度评价中，水域的分类精度较高，道路的分类精度较低，在道路的误分中，划分为土地的居多，占误分总量的67.01%。

表2　系统抽样方法的遥感影像分类结果精度评价

由表2看出，系统抽样方法获取的遥感影像的分类结果的总体精度为85.09%，Kappa系数为76.95%，在各类的分类精度评价中，水域的分类精度相对较高，而建筑的分类精度较低，其中，划分为土地的居多，占误分总量的75.28%。

表3　传统分层抽样方法的遥感影像分类结果精度评价

由表3看出，分层抽样方法对遥感影像分类结果的精度评价的总体精度为86.26%，Kappa系数为79.25%。其中水域的分类精度较高，道路的分类精度较低，由于低分辨率的遥感影像的空间分辨率较低，容易产生混合像元，导致土地类型的边缘不清晰，从而影响遥感影像的分类；同时，由于土地、道路、建筑的光谱特征相近，低分辨率遥感影像所选择的波段不能很好地区别土地、道路、建筑三种土地类型，造成混分、误分现象，从而导致在分类结果中，道路误分为土地的居多，占误分总量的55.38%。

由表1-表3看出，三种传统抽样精度评价中，系统抽样的总体精度与Kappa系数值相对略低，而传统分层抽样方法得到的总体精度与Kappa系数值相对略高。这是由于在系统抽样中，样本点等间隔规律分布，对于总体有周期性变化的样本点，评价结果易产生偏差，而土地类型的分布在空间上具有相关性，采用系统抽样选择的样本点易产生周期性规律，从而导致精度评价结果较低。而在分层抽样中，各层样本量的确定是按比例分配，而简单随机抽样与系统抽样方法未考虑各层样本量情况，样本点的分布有可能集中在某一层上，从而导致总体精度略低。

2.3空间抽样方法精度评价

空间自相关性是空间抽样研究的前提和基础，对采用传统抽样方法获得的2650个样本单元进行空间自相关显著性分析。由式(4)求得Moran’s I指数为0.206309，标准化Z值为9.182086，Z值远大于显著水平99%时的临界值2.58，因此，土地利用类型之间的自相关程度非常显著。考虑空间要素之间的相关性，采用空间自相关系数0.21作为空间抽样中确定其样本量的条件，空间分层抽样的总样本量n′为：

n′=n(1-r′)=2103

(9)

在空间分层抽样中，各层样本量的确定采用比例分配，因此，土地层、建筑层、水域层、道路层的样本量分别为1042、369、250、442，样本点按照空间分层抽样模型，等比随机分布在分类图上，如图7所示。

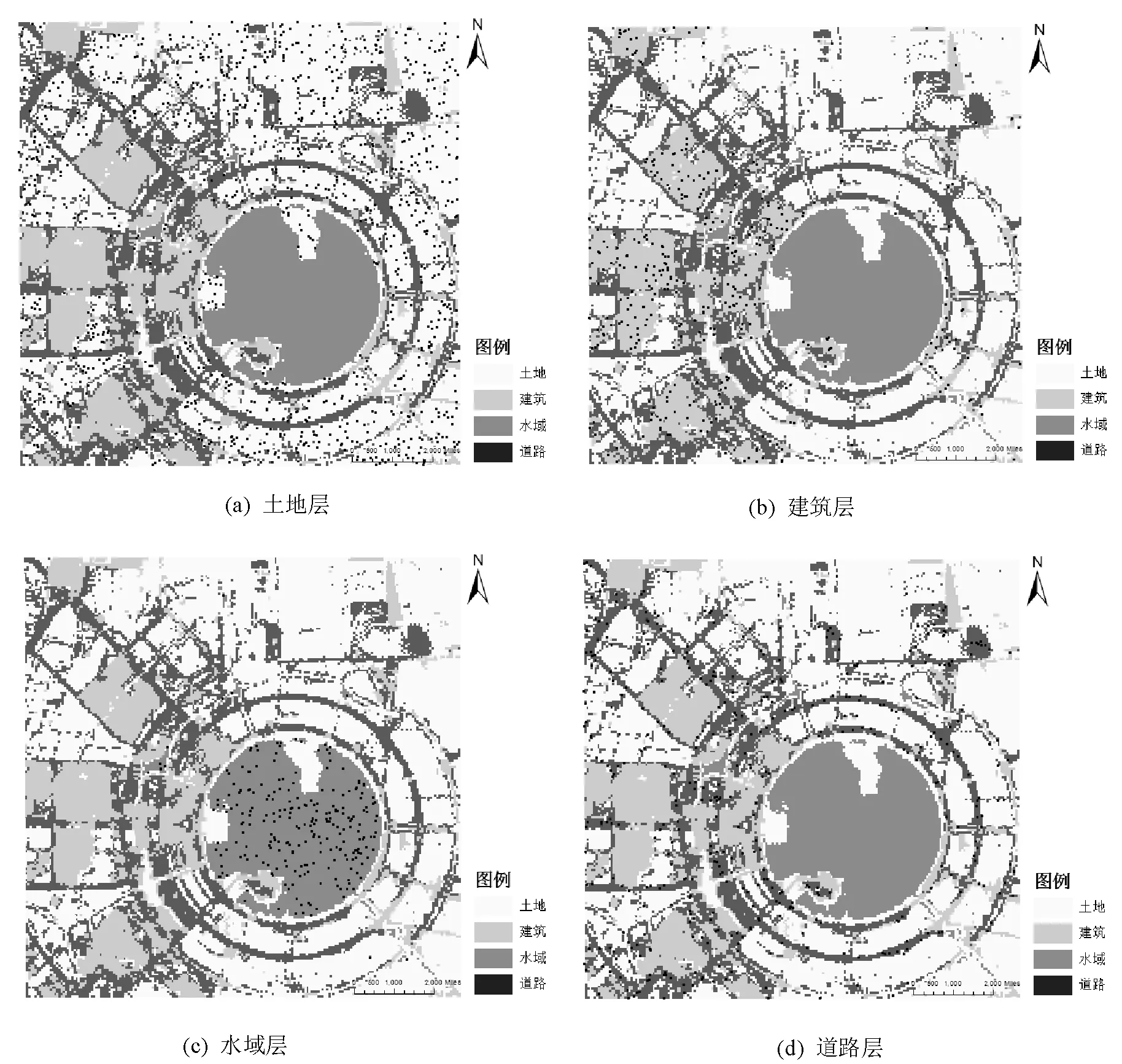
图7　空间分层抽样中各层样本点的空间分布

采用3 m高分辨率遥感影像对30 m低分辨率遥感影像分类结果进行精度评价和分析，结果如表4所示。

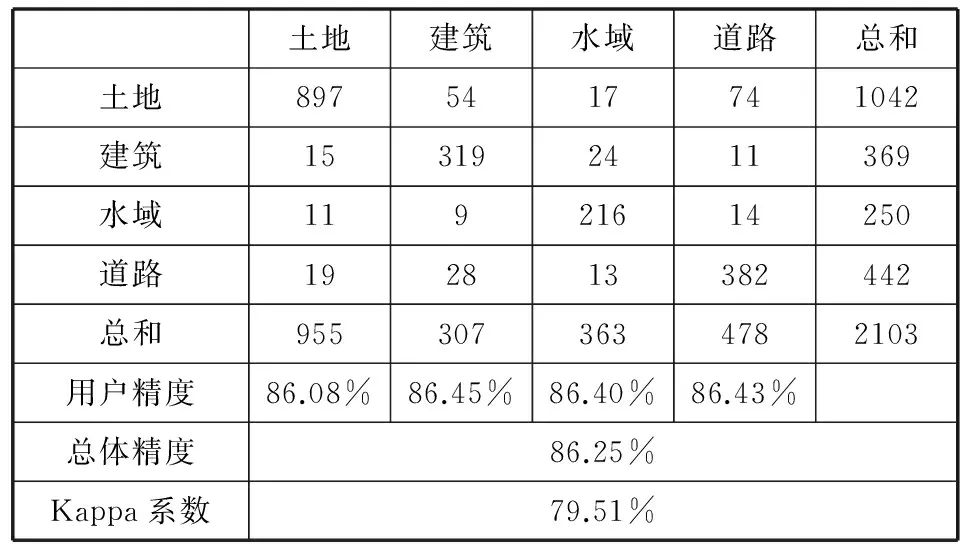
表4　空间抽样方法的遥感影像分类结果精度评价

由表4看出，采用Moran’s I指数的空间抽样方法获取的遥感影像分类结果的总体精度为86.25%，Kappa系数为79.51%，与传统的分层抽样方法获取的结果基本一致。但是由于空间抽样方法针对空间事物特有的空间结构，通过空间相关性分析，解决了样本量的冗余问题，样本量比传统的方法减少了20%。因此可以在保证精度的前提下，提高精度评价的检验效率。

3结语

本文针对遥感影像分类结果的特点，采用Moran指数对传统抽样理论中样本量的确定方法进行优化，并且利用空间抽样模型和传统抽样模型(简单抽样、系统抽样和分层抽样)对遥感影像分类结果进行精度评价与对比分析，研究结果表明：

(1) 与传统抽样的遥感影像分类结果的精度评价方法相比，由于考虑了空间要素之间的相关性，空间分层抽样方法的遥感分类结果精度评价方法不仅可以有效地降低样本量，而且可以合理地选取样本点，减少样本冗余，因此，可以应用于遥感影像分类结果的精度评价。

(2) 由于低分辨率遥感影像的空间分辨率较低，造成土地类型的边缘不清晰，容易产生混合像元，导致遥感影像的分类结果之间存在误差；同时，由于土地、道路、建筑的光谱特征相近，低分辨率遥感影像所选择的波段不能很好地区别土地、道路、建筑三种土地类型，从而导致了遥感影像分类结果的混分、误分现象。

(3) 不同的抽样方法对遥感影像分类结果的对比分析显示不同的抽样方法对遥感影像分类结果的精度评价具有不同的影响。但是，考虑到样本量及精度检验效率问题时，空间分层抽样的精度评价方法优于传统的精度评价方法，因此，可以在遥感影像分类结果精度评价中广泛的应用。

参考文献

[1] 张霞,庄智,张旭凯,等.秦皇岛市海岸线遥感提取及变化监测[J].遥感技术与应用,2014,29(4):625-630.

[2] 朱榴骏,肖鹏峰,冯学智,等.基于直方变差图的土地覆盖数据集多尺度精度评价[J].遥感学报,2013,17(6):1459-1474.

[3] 杨永可,肖鹏峰,冯学智,等.大尺度土地覆盖数据集在中国及周边区域的精度评价[J].遥感学报,2014,18(2):453-475.

[4] Dihkan M,Guneroglu N.Remote sensing of tea plantation using an SVM classifier and pattern-base accuracy assessment[J].International Journal of Remote Sensing,2013,34(23):8549-8565.

[5] 杨彬,李旭东,晏磊,等.航空遥感图像拼接算法及其精度评价[J].计算机工程,2014,40(3):253-257.

[6] Chen L G,Li Y K,Yang X Y,et al.Accuracy assessment of land use/cover classification from different seasons based on remote sensing imagery:A case study of Lianyungang city,China[J].Journal of China University of Mining and Technology,2013,42(5):873-879.

[7] 姜成晟,王劲峰,曹志冬.地理空间抽样理论研究综述[J].地理学报,2009,64(3):368-380.

[8] 张焕雪,李强子,文宁,等.农作物种植面积遥感抽样调查的误差影响因素分析[J].农业工程学报,2014,30(13):176-184.

[9] Matheron G.The Theory of Regionalized Variables and Its Applications[D].Fontainbleau: Ecole de Mines,1971.

[10] Li L F,Wang J F,Liu J Y.Optimization of decision-making for spatial sampling in remote sensing survey of land[J].Science in China (Series D),2004(10):975-982.

[11] Wang J F,Zhuang D F,Li L F.Spatial sampling design for monitoring the area of cultivated land. International Journal of Remote Sensing[J].2002,13(2):263-284.

[12] 王振华.空间数据质量抽样检验与控制的理论、方法和应用[D].上海:同济大学,2011.

[13] 刘旭拢,何春阳,潘耀忠,等.遥感图像分类精度的点、群样本检验与评估[J].遥感学报,2006,10(3):366-372.

[14] 陶吉兴,傅伟军,姜培坤,等.基于Moran’s I和地统计学的浙江森林土壤有机碳空间分布研究[J].南京林业大学学报:自然科学版,2014,38(5):97-101.

[15] 孙皓晗.空间分层抽样在森林覆盖监测中的应用研究[D].江苏:南京林业大学,2013.

收稿日期：2014-12-15。国家自然科学基金项目(61272098)；国家重点基础研究发展计划项目(2012CB316200)；上海市自然科学基金项目(13ZR1455800)；上海高校优秀青年培养项目(B-5409-11-0012)；海洋赤潮灾害立体监测技术与应用国家海洋局重点实验室开放研究基金课题(MATHAB201307)。黄冬梅，教授，主研领域：WebGIS，智能信息处理，辅助决策系统。陈珂，硕士生。王振华，博士。刘爽，博士。

中图分类号TP751.1

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.044

ACCURACY ASSESSMENT METHOD FOR REMOTE SENSING IMAGE CLASSIFICATION RESULTS BASED ON SPATIAL SAMPLING THEORY

Huang DongmeiChen KeWang ZhenhuaLiu Shuang

(SchoolofInformation,ShanghaiOceanUniversity,Shanghai201306,China)

AbstractThe accuracy of classification results of remote sensing images has an important effect on the application and analysis of remote sensing information. The accuracy assessment method of classification results of remote sensing image based on traditional sampling mode is affected by the sample size and spatial layout, and has the problems of low efficiency and information redundancy, etc. In this paper, by using the correlation of spatial data, we applied the spatial sampling theory to accuracy assessment of the classification results of remote sensing image, through comparison it with traditional sampling method, we found that the application of spatial sampling methods in accuracy assessment of the results not only reduces the data redundancy, it also improves the efficiency and accuracy of the test as well.

KeywordsRemote sensing classificationAccuracy assessmentSampling theoryError matrix