I-VLDNS：一种改进的线性判别子空间模式识别算法

莫京兰　朱广生　吕跃进

1(广西科技大学鹿山学院　广西 柳州 545616)2(广西科技大学　广西 柳州 545616)3(广西大学数学与信息科学学院　广西 南宁 530004)



I-VLDNS：一种改进的线性判别子空间模式识别算法

莫京兰1,3朱广生2吕跃进3

1(广西科技大学鹿山学院广西 柳州 545616)2(广西科技大学广西 柳州 545616)3(广西大学数学与信息科学学院广西 南宁 530004)

摘要针对现有模式判别分析方法中普遍存在的子空间优化与“小样本”问题，首先剖析总体、类内以及类间三种散布矩阵的零空间的物理含义，深入阐释有效零空间与有效线性判别零空间核心原理；其次，研究始空间中总体、类间散布矩阵与有效零空间、有效值域空间上的总体、类间散布矩阵关于特征值与特征向量之间的关联关系，并且获取类内散布矩阵零空间、值域空间上关于Fisher线性判别率的关键结论；最后，基于有效线性判别零空间理论，设计出一种改进的线性判别子空间模式识别算法，即I-VLDNS。通过相关数据集模拟实验表明，I-VLDNS算法在模式识别分析性能、精确度以及鲁棒性上均得到进一步优化与提高。

关键词模式识别线性判别分析有效零空间值域空间I-VLDNS

0引言

随着科技信息化进程的不断推进，模式识别作为热点研究方向，得到了越来越多地关注，并在人工智能、数据挖掘等领域得到深入应用。模式分析是模式识别的核心技术之一，作为模式分析的一个关键研究点，子空间分析技术依靠不同映射方式对应的不同优点，已普遍应用于模式识别、计算机视觉分析、生物特征与数据识别，并在数据挖掘领域具有无限广阔地应用前景。因此，如何有效选取与处理大规模海量数据信息中的有效判别数据信息，深入研究子空间分析技术具有非常重要的意义。

近年来，国内外学者对子空间分析技术进行了深入研究，文献[1]揭示了模式分析中普遍存在的“小样本”问题，其常常存在于THz-TDS模式识别问题中。为了有效处理“小样本”问题，改进并提高模式分析中的优化性能，专家学者们重点研究线性判别分析技术。文献[2,3]通过摒弃总体散布矩阵的零空间，从值域空间中选取有效的特征向量，设计出相对应的线性判别分析方法。然而，该方法选取范围较狭窄，仅选取了总体类内散布矩阵的零分量。文献[4,5]通过一系列方法，从零空间与值域空间中得到了最优判别向量，但是，对应于零特征值与较小特征值的特征向量敏感度较高，易受到训练样本数量影响，从而发生变化。文献[6]在文献[4,5]的基础上，设计出一种广义零空间不相关Fisher判别分析方法。此方法尽管在线性判别分析上有所改进与优化，但是仍受到零空间维度大小影响，具有一定局限性。文献[7]提出一种主分量零空间分析方法，该方法通过获取整体数据信息的主分量子空间。依次得到每个子类近似零空间，但是，该方法易造成一定风险，如丢失相关主分量判别数据信息等。文献[8]提出一种可并行处理Fisher最大与最小的判别准则的最佳对称零空间准则，对“小样本”问题得到了进一步优化，然而其方法对计算处理能力要求较高，对模式识别分析性能造成一定影响。除了上述研究之外，文献[9-12]同样从总体散布矩阵、类内散布矩阵以及类间散布矩阵的零空间着手，对模式判别分析方法进行深入改进与研究，然而均存在一定应用局限性。

针对现有模式判别分析方法中普遍存在的子空间优化与“小样本”问题，本文首先剖析总体、类内以及类间三种散布矩阵的零空间的物理含义，深入阐释有效零空间与有效线性判别零空间核心原理，证明相关理论命题；其次，研究不同子空间中类间散布矩阵相互之间的关联关系；最后，基于有效线性判别零空间理论，设计出一种改进的线性判别子空间模式识别算法，即I-VLDNS。通过相关数据集模拟实验表明，I-VLDNS算法均比同类型的几种算法更加优秀，在模式识别分析性能、精确度以及鲁棒性上得到了进一步优化与提高。

1零空间物理含义

(1)

(2)

(3)

其中μi表示ωi类的的均值向量，μ0表示整个数据信息的均值向量，可知：

(4)

定理1类间散布矩阵SB满足如下等式：

(5)

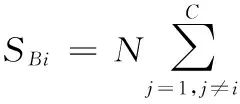
证明：首先依据式(2)，有：

其次导入式(1)中，可知：

从而获取总体类间散布矩阵SB与各自子类的类间散布矩阵SBi相互之间的关联关系，如式(5)。定理1揭示了SB与SBi相互之间的关联关系。

假定φ1,φ2,…,φd,…,φn表示ST的特征向量，且保证前半部分φ1,φ2,…,φd对应于非零特征值，后半部分φd+1,φd+2,…,φn对应于零特征值，其中d=Rank(ST)。可知，前半部分φ1,φ2,…,φd形成ST的值域空间，使用Φn×d表示，后半部分φd+1,φd+2,…,φn形成对应的零空间。

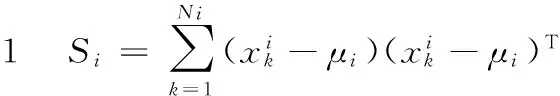
图1　总体、类内散布矩阵的零空间物理含义分析结构图

2有效判别零空间性质分析

2.1有效子空间

假定总体训练测试样本N满足n>N-1，对于SW、SB、ST的秩满足以下结论，可知：rank(ST)≤N-1;rank(SW)≤N-C;rank(SB)≤C-1。其中SW、SB、ST均属于奇异矩阵[13]。实际运用过程中满足N>C，则各个散布矩阵的秩关系如下：rank(ST)>rank(SW)>rank(SB)。此时参照推论1可知各个散布矩阵零空间满足如下关系：

Null(SB)∩Null(SW)=Null(ST)

(6)

因为Null(ST)上的类间与类内相隔长度等于零，满足分类无效性质，定义为无效零空间。与之对应，正交补空间Range(ST)=L(Φ)定义为有效子空间，其中正交基由Φn×d=[φ1,φ2,…,φd]表示。

2.2有效零空间

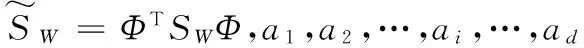
Null(SW)=L(Φa1,…,Φai)⊕Null(ST)

(7)

2.3有效判别零空间

证明：

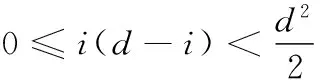
(8)

(9)

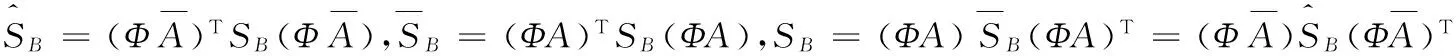
(10)

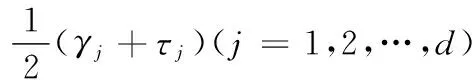
(11)

证明：V1、V2与V3上的类内相隔长度依次属于{0}，/{0}与，并且类间相隔长度依次是γj1，τj2与。因γj1≥0,τj2≥0，且。那么引理2得证。

V1、V2与V3依次是d×i，d×(d-i)与d×d的散布矩阵。因为d>d-i>i，V1、V2与V3在其子空间上的计算性能逐渐降低。零空间L(V1)具有计算性能以及无穷大Fisher判别率等优点，定义为有效判别零空间。

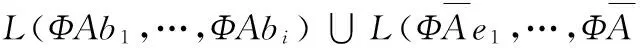
3I-VLDNS算法

通过对有效判别零空间的深入研究，提出一种改进的线性判别子空间模式识别算法，即I-VLDNS，该算法的详细步骤如下：

步骤1计算ST在零特征值上与之对应的特征向量φ1,φ2,…,φd。

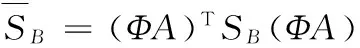
步骤6将测试样本向量x投影于特征空间上，获取对应的投影向量z=(ΦP)Tx，参照最近邻分类准则判别其投影向量z的归属类型。

若x投影于ST的值域空间上，可获取一个低维度的测试样本向量，即y=ΦTx。因为任何一个测试样本都覆盖于ST的零空间中心点，那么在模式分类作用上，此零空间具有无效性。虽然此零空间对模式分类精确性零干扰，然而选择值域空间L(Φ)得到了降维，并优化了计算性能。

4模拟实验与结果分析

分别从Oracle数据库、THz-TDS数据集两个环境下对I-VLDNS算法进行模式实验，如下：

4.1Oracle数据库

在时间选择、拍照条件、人脸表情细节等方面处于各不相同的情况下，选择50个不同人物，对每个人物提取15人脸精确图像(精确度：136×96像素、灰度：0～255)，并存入Oracle数据库中。模拟实验中，保证图像的原始性。随机提取所有人物的k张图像信息作为模拟实验的训练样本，剩余50-k张作为测试样本。模拟实验过程中，利用最近邻分类方法，依次对k值进行选取(k=3,4,5,6)，最终数据是10次模拟实验数据的平均值。

若训练样本大小超过整体实验样本大小的一半，那么V=[V2,V1]，不然V=[V1,V2]。虽然类内散布矩阵的零空间具有多样化的Fisher判别数据，但是其子空间易受外界影响，从而发生变化。在训练样本大小逐渐提升的情况下，此类内散布矩阵的零空间逐渐退化。因此，在优化性能方面，L(V2)比L(V1)更佳。如图2所示。

图2　Oracle数据库上的模式识别误差对比

从图2中可知，在平均、最大模式识别率方面，I-VLDNS算法比同类型的其他几种算法更好。当不断添加训练样本数量大小时，文献[6]算法、文献[7]算法以及I-VLDNS算法的模式识别误差下降，且误差的标准偏差均有降低，其中I-VLDNS算法的标准偏差是最小的。实验表明，与文献[6]算法、文献[7]算法相比，I-VLDNS的算法鲁棒性最优。与此同时，对比文献[6]算法，若子空间维度越低，I-VLDNS算法的模式识别率也越高，当训练样本数量大小是3时处于最优状态。

4.2THz-TDS数据集

本次实验依次选取水杯、牛奶、花生、衣服、毛巾、咖啡、茶叶、桌子、塑料、手机、皮鞋、树木等12种各不相同的样本物体，采用THz-TDS系统获取与样本物体相对应的THz-TDS信号。THz-TDS系统可发射0.1 THz至4.0 THz的THz波，将其系统设置于透射模式，采样步长选择44.4飞秒，时间参数设置为40毫秒。如表1所示，实验采用0.2 THz至2.22 THz波长区域之间的透射谱，其长度是144。训练样本数量大小依次选取实验样本数量大小的1/5，1/4，1/3与1/2。最终数据是10次模拟实验数据的平均值，如图3所示。

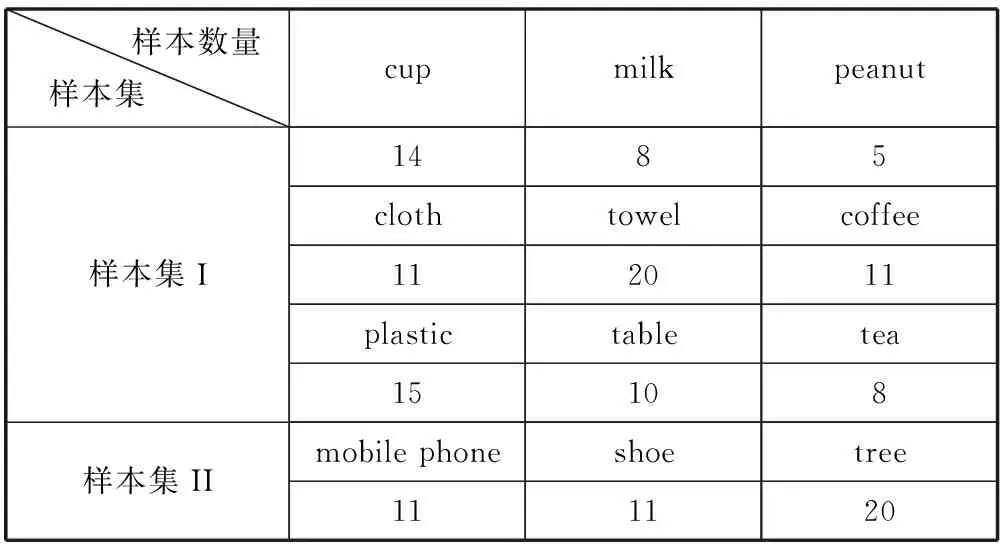
表1　THz-TDS数据集中各类样本的透射谱数据表

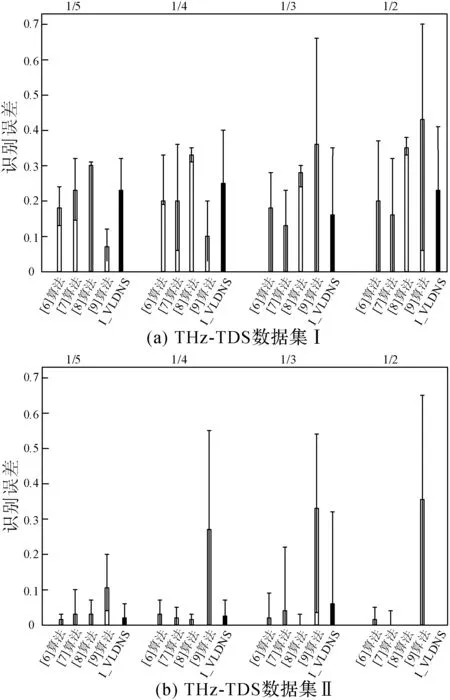
图3　THz-TDS数据集上模式识别误差对比

首先，数据集I上的THz-TDS信号处于次优化状态，并且伴有一定的噪声干扰；其次，数据集II上的THz-TDS信号的各类样本的透射谱质量得到明显提升，并且具有相对不错的分辨率。

从图3中可知，在THz-TDS数据集I中，文献[6]算法、文献[8]算法与I-VLDNS算法上的测试结果近似一致。然而当子空

间维度处于更低状态时，I-VLDNS算法依然达到相同的模式识别性能。在THz-TDS数据集II中，特别是当训练样本数量大小占实验样本数量大小的1/2时，I-VLDNS算法能够达到100%的模式识别率。

因为整体数据信息覆盖于总体散布矩阵的零空间中心点，所以，在总体散布矩阵的值域空间中，存在有训练样本数据中的判别信息。从而更深入分析了在较低维度大小的子空间内，可依据类内散布矩阵获取原始空间中的判别信息。I-VLDNS算法正是基于这一点，在模式识别分析性能、精确度以及鲁棒性上具有良好效果。

5结语

本文针对现有模式判别分析方法中普遍存在的子空间优化与“小样本”问题，首先阐述并分析证明了总体、类间以及类内散布矩阵的零空间物理含义；其次，研究了原始空间中总体、类间散布矩阵与有效零空间、有效值域空间上的总体、类间散布矩阵关于特征值与特征向量之间的关联关系；最后，基于有效线性判别零空间理论，设计出一种改进的线性判别子空间模式识别算法，即I-VLDNS。在小样本情况下，该算法可提取更加多样化的判别信息，与同类型的其他算法相比，I-VLDNS算法在模式识别率、精确度以及鲁棒性上具有更大优势。

参考文献

[1] 边肇棋,张学工.模式识别[M].2版.北京:清华大学出版社,2000.

[2] Nikolaos Gkalelis,Vasileios Mezaris,Ioannis Kompatsiaris.Mixture Subclass Discriminant Analysis[J].IEEE Signal Processing letters,2011,18(5):319-322.

[3] Xiaoning Song,Jingyu Yang,Xiaojun Wu,et al.An optimal symmetrical null space criterion of Fisher discriminant for feature extraction and recognition[J].Soft Computing-A Fusion of Foundations,Methodologies and Applica- tions,2011,15(2):281-293.

[4] Vaswani N,Chellappa R.Principal components null space analysis for image and video classification[J].IEEE Trans on Image Processing,2006,15(7):1816-1830.

[5] 杨健.线性投影分析的理论与算法及其在特征抽取中的应用研究[D].南京,南京理工大学,2002.

[6] 谢维信,蒲莉娟,裴继红.基于值域空间中类零子空间分析的模式判别[J].信号处理,2012,28(10):1315-1360.

[7] Jiang X D.Linear subspace learning-based dimensionality reduction[J].IEEE Signal Processing Magazine,2011,28(2):16-26.

[8] Safayani M,Manzuri Shalmani M T.Heteroscedastic Multilinear Discriminant Analysis for Face Recognition[C]//2010 International Conference on Pattern Recognition,2010:4287-4290.

[9] Connie T,Jin A,Ong M.An automated palmprint recognition system[J].Image and Vision Computing,2005,23(5):501-515.

[10] Michael Schmuker,Gisbert Schneider.Processing and classification of chemical data inspired by insect olfaction[J].Proceedings of the National Academy of Sciences,2007,104(51):20285-20289.

[11] 杨健,杨静宇,叶晖.Fisher线性鉴别分析的理论研究及其应用[J].自动化学报,2003,29(4):482-493.

[12] John Wright,Allen Y Yang,Arvind Ganesh,et al.Robust Face Recognition via Sparse Representation[J].IEEE Trans On Pattern Analysis and Machine Intelligence,2009,31(2):210-227.

[13] 蒲莉娟.模式判别中的子空间分析方法研究[D].西安,西安电子科技大学,2013.

收稿日期：2015-01-28。国家自然科学基金项目(70861001)；广西高等学校立项科研项目(2013LX095)。莫京兰，讲师，主研领域：粗糙集，数据挖掘，运筹学与控制论。朱广生，硕士。吕跃进，教授。

中图分类号TP391.4

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.040

I-VLDNS: AN IMPROVED LINEAR DISCRIMINATIVE SUBSPACE PATTERN RECOGNITION ALGORITHM

Mo Jinglan1,3Zhu Guangsheng2Lü Yuejin3

1(LushanCollegeofGuangxiUniversityofScienceandTechnology,Liuzhou545616,Guangxi,China)2(GuangxiUniversityofScienceandTechnology,Liuzhou545616,Guangxi,China)3(SchoolofMathematicsandInformationSciences,GuangxiUniversity,Nanning530004,Guangxi,China)

AbstractIn light of the problems of subspace optimisation and “small sample size” commonly existed in current pattern discriminative analysis methods, in this paper we first analyse the physical meaning of null-space of total scatter matrix, between-class scatter matrix and within-class scatter matrix, and thoroughly explain the core principles of valid null-space and valid linear discriminative null-space. Secondly, we study the association relationship of eigenvalues and eigenvectors with regard to the total scatter matrixes and between-class scatter matrixes of both the original space and the valid null-space and valid range-space, and obtain the key conclusions about Fisher linear discriminative probability of within scatter matrix null-space and within scatter matrix range-space. Finally, based on effective linear discriminative null-space theory, we design an improved linear discriminative subspace pattern recognition algorithm (I-VLDNS). It is demonstrated through correlated dataset simulation experiments that the I-VLDNS gains further optimisation and improvement in analysis performance of pattern recognition, accuracy and robustness.

KeywordsPattern recognitionLinear discriminative analysisValid null-spaceRange-spaceI-VLDNS