基于LTE定位参考信号的时频二维联合时延估计算法

刘韦韦　林基明　后　茜　丁　进

(桂林电子科技大学信息与通信学院　广西 桂林 541004)



基于LTE定位参考信号的时频二维联合时延估计算法

刘韦韦林基明后茜丁进

(桂林电子科技大学信息与通信学院广西 桂林 541004)

摘要LTE(LTE Positioning Protocol)定位参考信号的频域梳状结构特点会导致时域相关检测出现周期性峰值。当移动台与基站之间的距离较大时，则会出现测距模糊问题。为了解决这个问题，提出一种基于LTE定位参考信号的时频二维联合时延估计算法。该算法首先在频域上以较大的滑动步长对接收信号做滑动相关，快速找到OFDM符号的粗略起始时刻，然后将本地定位参考信号与滑动窗内的接收信号做相关，并提取整数倍传输时延，最后在频域上利用子载波间的相位差估计小数倍传输时延，从而获得精确时延估计。仿真结果表明：该算法有效地解决了测距模糊问题，且在信噪比等于10 dB时，其测距精度在4米左右。

关键词长期演进定位参考信号测距模糊时频二维联合时延估计

0引言

随着移动互联网的发展，基于位置的服务LBS(Localization-Based Services)已经深入人们生活的方方面面。如导航定位、智能交通、移动社交网络、救援定位等，其对定位精度的要求也越来越高[1]。因此，长期演进LTE(Long-Term Evolution)作为下一代无线通信技术[2]，研究其终端定位技术具有重要的实际意义。

3GPP在LTE定位协议LPP(LTE Positioning Protocol)[3]中提出3种定位方法：增强型小区号识别定位E-CID(Enhanced Cell-Identity)、辅助全球卫星导航系统定位A-GNSS(Assisted-Global Navigation Satellite System)以及观测到达时间差定位OTDOA(Observerd Time Difference of Arrival)。其中，E-CID定位技术的精度最低但实现较为简单，常与其他定位方法联合实现定位。A-GNSS定位技术的定位精度最高，但在室内和城市峡谷等环境下，其定位精度严重下降。因此，这两种定位技术在实际应用中均存在局限性。而对于OTDOA定位技术，虽然定位精度不及A-GNSS定位技术，但对环境和设备的要求较低，可以与A-GNSS定位技术形成优势互补，因此OTDOA定位技术成为LTE系统定位的主要备选方法。对于OTDOA定位技术，其定位精度主要取决于到达时间TOA(Time Of Arrival)估计精度。目前，已有不少文献对基于LTE定位参考信号PRS(Positioning Reference Signal)的时延估计技术进行研究。文献[4-7]中提出采用传统或者改进的相关检测算法进行时延估计，但是此类算法的时延估计精度受限于系统采样间隔。为了提高时延估计精度，文献[8,9]中提出使用快速抛物线内插和时域内插的方法实现TOA估计，其精度能够突破系统采样间隔，但是它们未能利用OFDM信号频域特性。文献[10]提出一种信道和时延联合的最大似然ML(Maximum Likelihood)估计算法，其时延估计精度受设置的信道路径数的影响，同时巨大的运算量制约了实用性。另外，由于PRS的梳状导频结构特点引起时域信号出现一定的重复性，相关检测会出现周期性峰值，这使得测距不模糊距离变短。当移动台与基站之间的距离较大时，则会存在测距模糊问题，导致较大的距离估计误差。

本文根据LTE PRS信号的时频特性，提出一种基于LTE定位参考信号的时频二维联合时延估计算法。即首先在频域上以较大的滑动步长对接收信号做滑动相关，快速找到OFDM符号的粗略起始时刻；然后将本地定位参考信号与滑动窗内的接收信号做时域相关，并将相关峰值对应的时刻作为整数倍传输时延；最后在频域上利用子载波间的相位差估计小数倍传输时延。该算法可以有效地解决了测距模糊问题，时延估计不受限于系统采样周期。

1系统模型

1.1PRS的时频结构

LTE下行链路中的一个无线帧长度为10 ms，包括10个1 ms的子帧，每个子帧由两个0.5 ms的时隙构成。对于常规循环前缀CP(Cyclic Prefix)，每个时隙包含7个OFDM符号；对于扩展CP，每个时隙包含6个OFDM符号。3GPP在LTE协议[11]中定义了PRS专用于时延估计。PRS只在下行子帧配置为传输PRS的资源块中传输。在频域上，PRS以间隔6个子载波映射到资源单元上，形成“梳状”的频域结构；在时域上，每个定位子帧分配8个OFDM符号用于传输PRS。PRS的带宽和具体资源映射位置均有高层配置。图1为常规循环前缀、小区物理标识(PCI)为0和单天线下PRS的映射图。

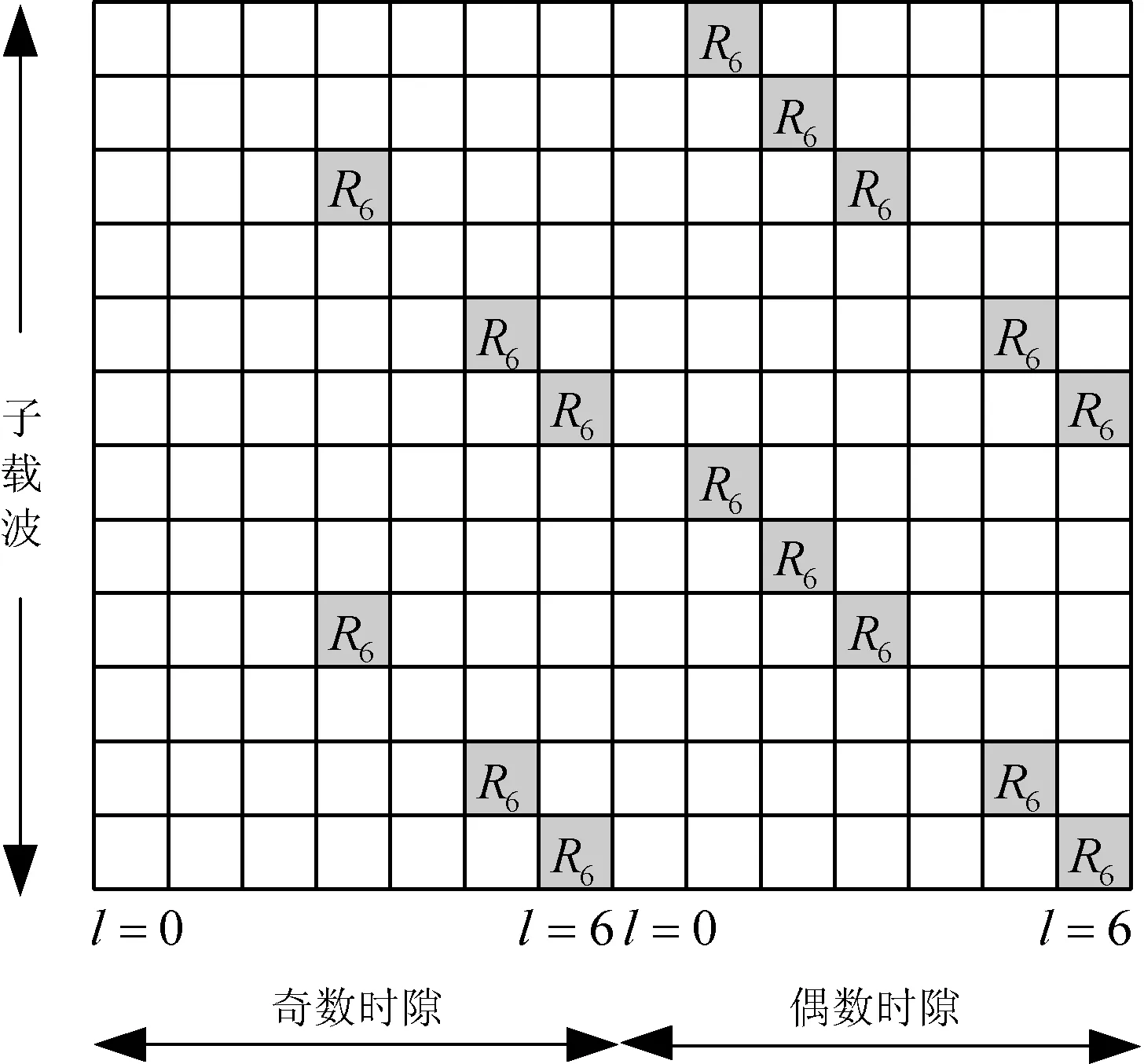
图1　定位参考信号映射图

1.2信号传输模型

在基站端，根据高层的参数配置产生定位参考序列，并将定位参考序列映射到物理资源单元中，最后经过快速傅里叶逆变换(IFFT)变换得到OFDM基带信号为：

(1)

其中，X(k)为定位参考序列，J为承载定位参考序列的子载波集合，N为FFT的大小，T为OFDM符号有效长度。

移动台与基站之间的多径信道可表示为：

(2)

其中，L为多径数目，hl和nl分别为第l径的衰落系数和时延。

信号经过无线多径信道后，移动台接收到的信号表示为：

(3)其中， θ=θI+θF为归一化传输时延，θI为整数倍传输时延，θF∈[-0.5,+0.5]为小数倍传输时延，w(n)为复高斯白噪声。

对y(n)做快速傅里叶变换(FFT)可以获得各个子载波上的数据，第k个子载波上的接收频域信号为：

(4)

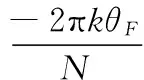
2时频二维联合时延估计算法

2.1问题分析

LTE定位参考序列具有较好的自相关特性，但由于在资源映射时，定位参考序列以间隔6个子载波映射到资源单元中，且只占用部分带宽。这种频域梳状结构会使得时域信号出现一定重复性[11]，即：

(5)

其中，Δ为间隔子载波数，l0为承载定位参考信号第一个子载波的序号，NJ为定位参考信号占用子载波总数。

利用定位参考信号良好自相关特性，将本地定位参考信号与接收定位参考信号建立相关。图2给出了基站与移动台之间的传输时延分别为0、170Ts、200Ts时的时域相关结果(其中纵坐标表示归一化相关值，横坐标表示信号时延)。如图2所示，除了主峰外，还带有周期性旁瓣，且最大不模糊距离为170Ts。当基站与移动台之间的传输时延等于200Ts时，此时相关峰值对应的时刻为30Ts，并作为时延估计值，则出现测距模糊问题。另外，相关检测法的时延估计精度受限于系统采样周期。

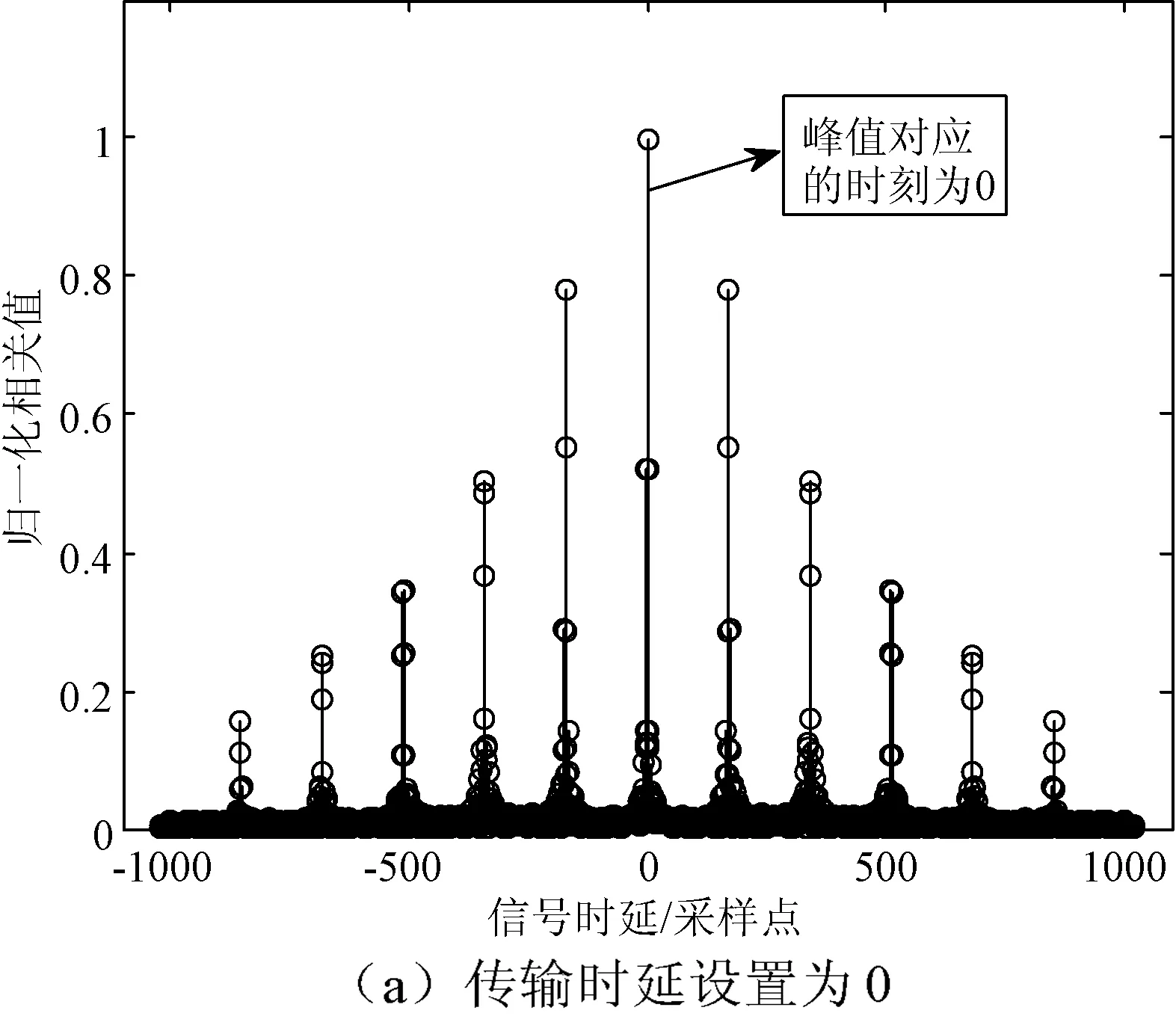
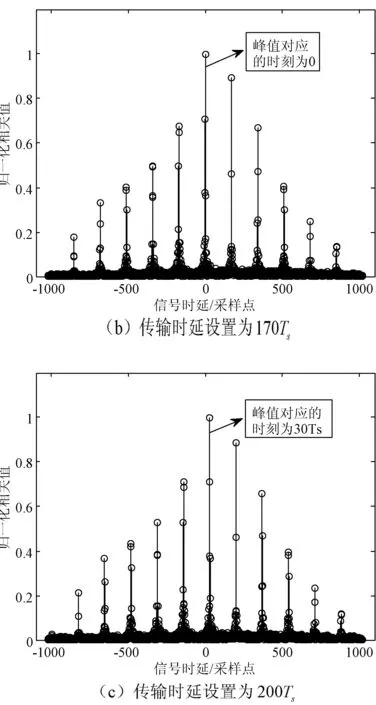
图2　定位参考信号时域相关

为了克服测距模糊以及时延估计受限于系统采样速率的问题，首先在频域上以较大的滑动步长对接收信号做滑动相关，迅速找到定位参考信号的粗略起始时刻。然后将本地定位参考信号与滑动窗内的接收信号做相关并估计整数倍传输时延。最后，在频域上利用子载波间的相位差估计小数倍传输时延。

2.2整数时延估计

整数时延估计分为整数时延粗估计和整数时延精估计两步。整数时延粗估计采用文献[9]中的时延估计方法，即以长度为N本地定位参考序列作为滑动窗，从时刻t0开始，将落入滑动窗中的接收信号变换到频域，记为Yt0(k),k=0,1,…,N-1。当滑动窗的起始位置落定位参考信号所在的OFDM符号Symbs的循环前缀范围内(如图3所示)时，Yt0(k) = α0(k)X(k)ejε0。其中，α0(k)是t0时刻接收信号的幅度衰减因子(由多径和噪声决定)，ε0为相位偏移。

图3　滑动相关窗起始位置示意图

在无线信道环境下，α0(k)和ε0均是未知的。对Yt0(k)和X(k)进行如下运算：

(6)

由式(6)可知，相位偏移不会影响C0值。故可利用此特点增大滑动窗每次滑动的步长。设每次滑动的步长为循环前缀长度，即NCP个采样点(如图4所示)。对以下这些时刻ti=ti-1+NCP,i=1,2,…，依次重复式(6)的操作，可以得到：

Yti(k)=αi(k)X(k)ejεi

(7)

(8)

然后，Ci,i=0,1,2,…中找到一个最大值，即：

(9)

将Cmax对应的时刻ti记为tc1，则tc1在Symbs的循环前缀所处区间内，此时时延误差在一个循环前缀长度范围之内。

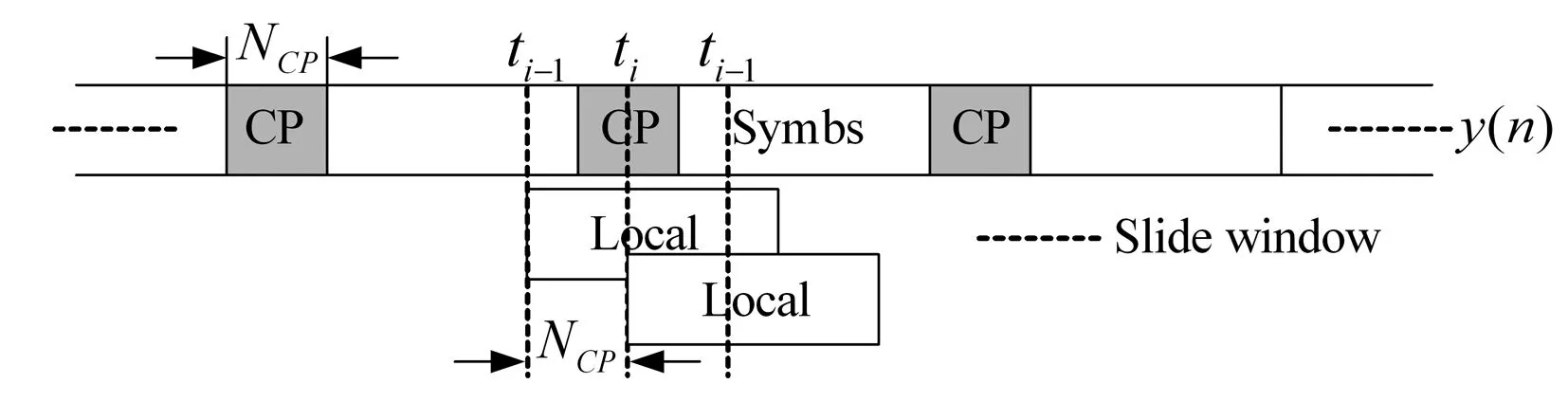
图4　快速滑动相关示意图

以tc1为起始点重新确定相关窗并进行整数倍传输时延精估计。首先取出滑动窗内的接收信号，记为y′(n)，然后利用本地定位参考信号与滑动窗内的接收信号做相关，将相关峰值对应的时刻作为整数倍传输时延精估计，即：

(10)

则整数倍传输时延为：

(11)

2.3小数时延估计

假设已经准确估计出整数时延并补偿上面所得的整数时延θI后，此时频域接收信号为：

(12)

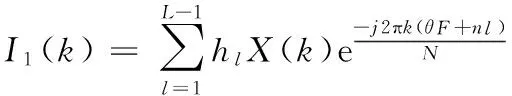
Q(k)=Z(k)X*(k)

(13)

然后，对式(13)进行迟滞m(m为正整数且为6的倍数)的差分相关处理，即：

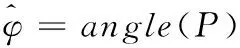
(15)

其中“angle(·)”表示取复数的相位。则小数倍传输时延估计为：

(16)

(17)

3算法仿真及性能分析

3.1时延估计的CRLB

本文提出的时延估计算包括整数时延估计和小数时延估计两部分。其时延估计精度主要取决于小数时延估计的性能。根据CRLB的定义[12]，推导出在高斯白噪声信道下小数时延估计的CRLB，并根据时延与距离之间的关系，则距离估计的CRLB为：

(18)

其中，σ2为噪声功率，M为定位子帧中的定位参考信号的个数，Xm(k)为第m个定位参考信号中第k个子载波上的频域数据。

3.2性能仿真

为了验证本文所提算法的性能，根据以上的理论分析，对其进行Matlab仿真。在仿真中，信号选用LTE下行链路的定位参考信号，采用典型的城市信道模型ITU-A作为仿真环境。ITU-A信道模型各径的归一化延迟分别为0、4、11、17、27、40个采样点，抽头功率分别为0、-1.0、-9.0、-10.0、-15.0、-20.0 dB。其余的仿真参数设置如表1所示。

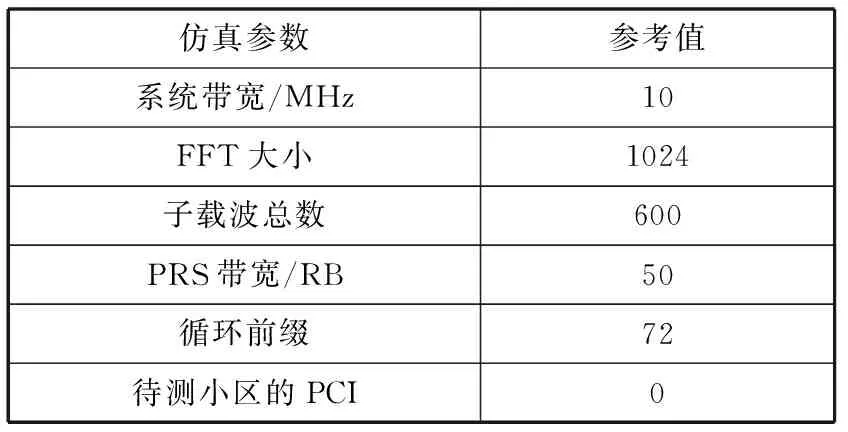
表1　仿真参数设置

3.2.1整数时延估计算法性能分析

假设移动台与基站间的传输时延为200Ts，信道选用ITU-A多径信道，信噪比等于30 dB。若直接利用本地定位参考信号与接收定位参考信号进行相关运算，相关结果如图5所示。峰值对应的时刻为30Ts，若以此作为时延估计，将给时延估计带来巨大误差。

图5　直接时域相关结果图

而本文所采用的整数时延估计方法，即以NCP为步长对接收信号做滑动相关，粗略估计定位参考信号的起始时刻，如图6所示。虽然滑动相关峰较为平坦，但没有旁瓣，将滑动相关峰值对应时延作为整数倍传输时延粗估计，此时的时延误差在循环前缀之内。

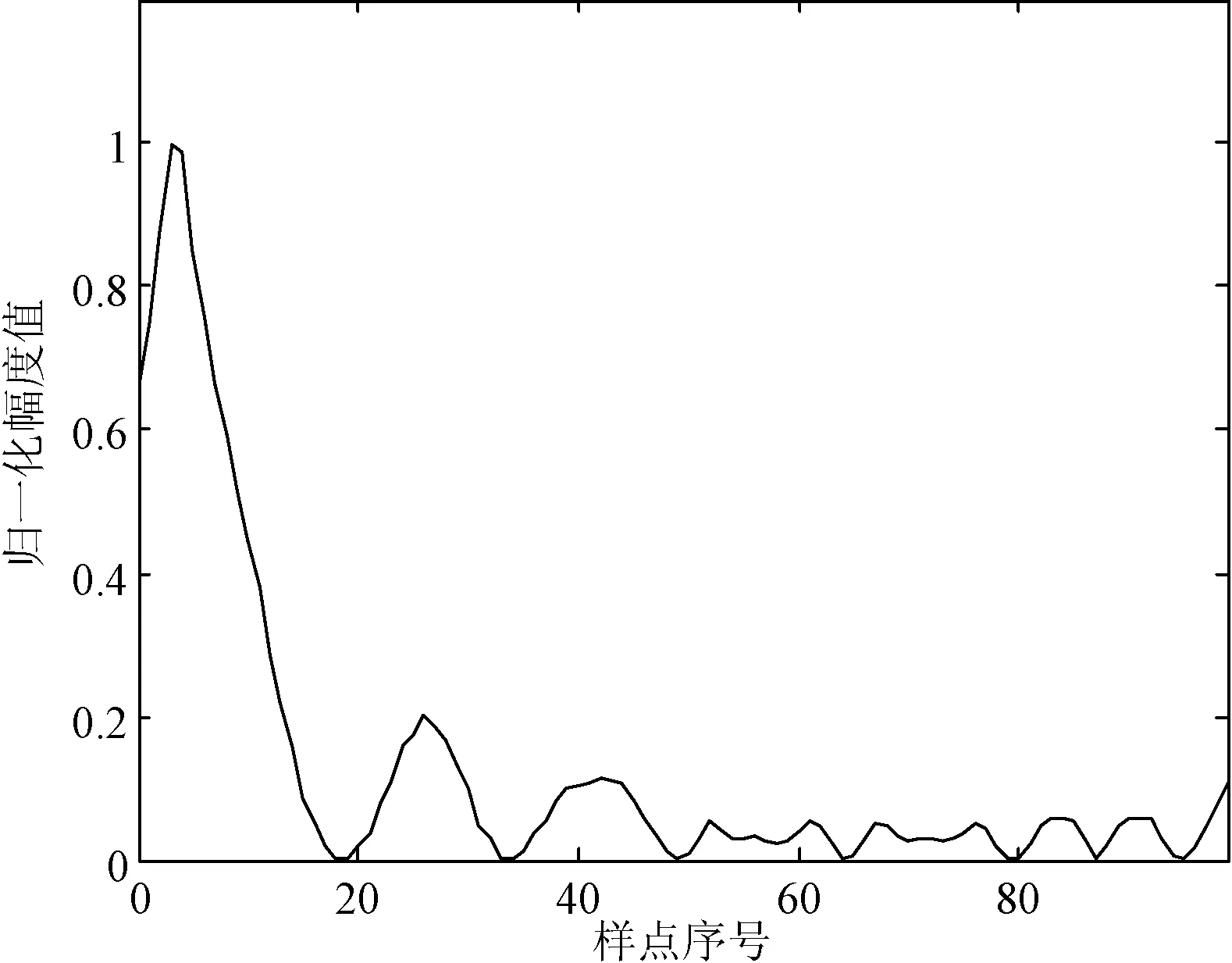
图6　滑动相关结果图

然后以粗估计结果为起始时刻重新确定相关窗，利用本地定位参考信号与窗内的接收定位参考信号做相关并以相关峰值对应的时刻作为整数倍传输时延精估计，如图7所示。仿真结果表明，当传输时延大于170Ts，该算法有效地克服测距模糊问题，能够准确估计整数时延。

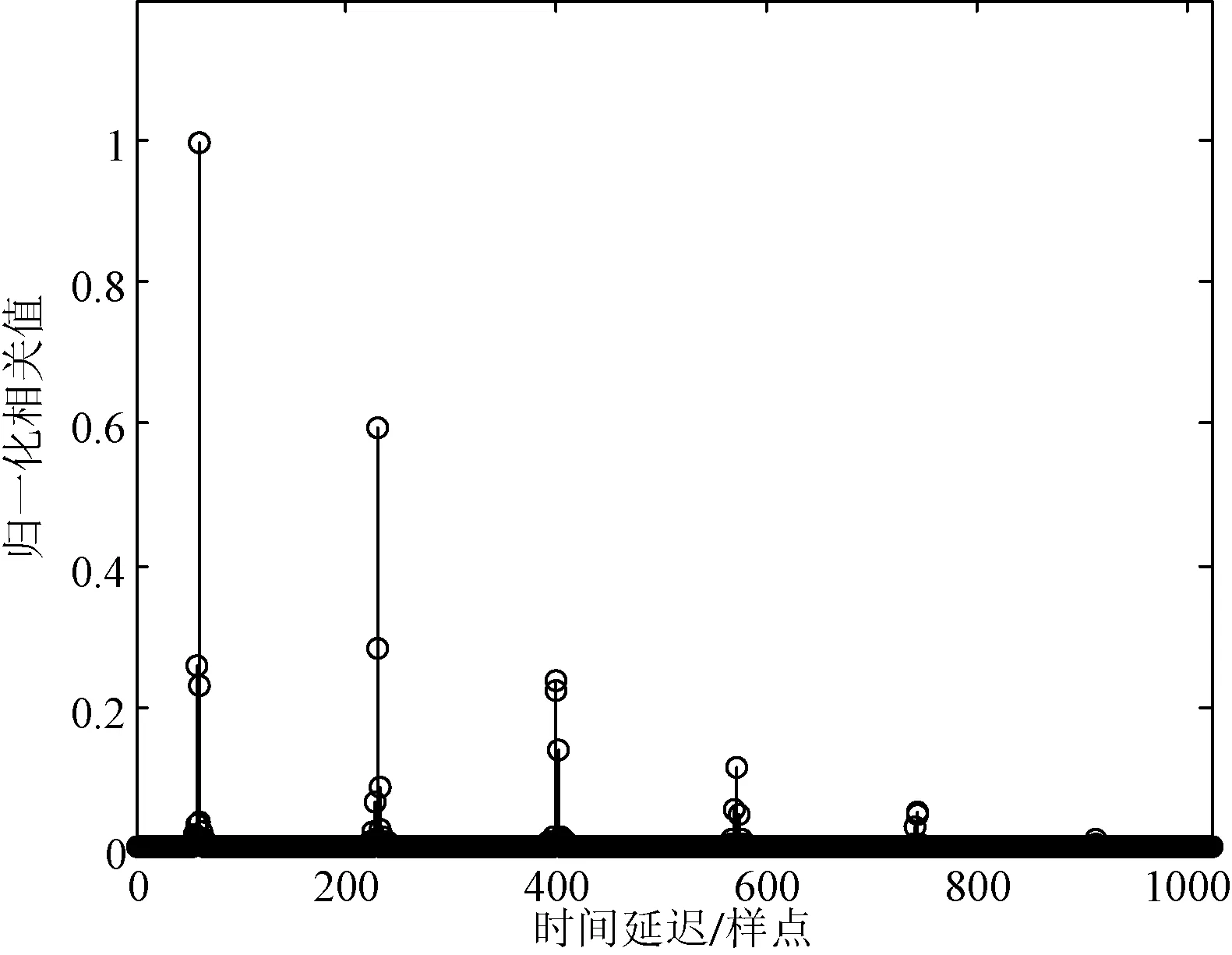
图7　时域相关结果图

3.2.2小数时延估计算法性能分析

首先，分析在高斯白噪声信道环境下间隔子载波数v取不同值对文中算法的时延估计精度的影响。图8给出了在信噪比为30 dB时，文中算法的小数时延估计的RMSE随间隔子载波数v的变化曲线。如图7所示，当间隔子载波数v的取值在52到246区间内时，该算法均能够获得较高的时延估计精度。

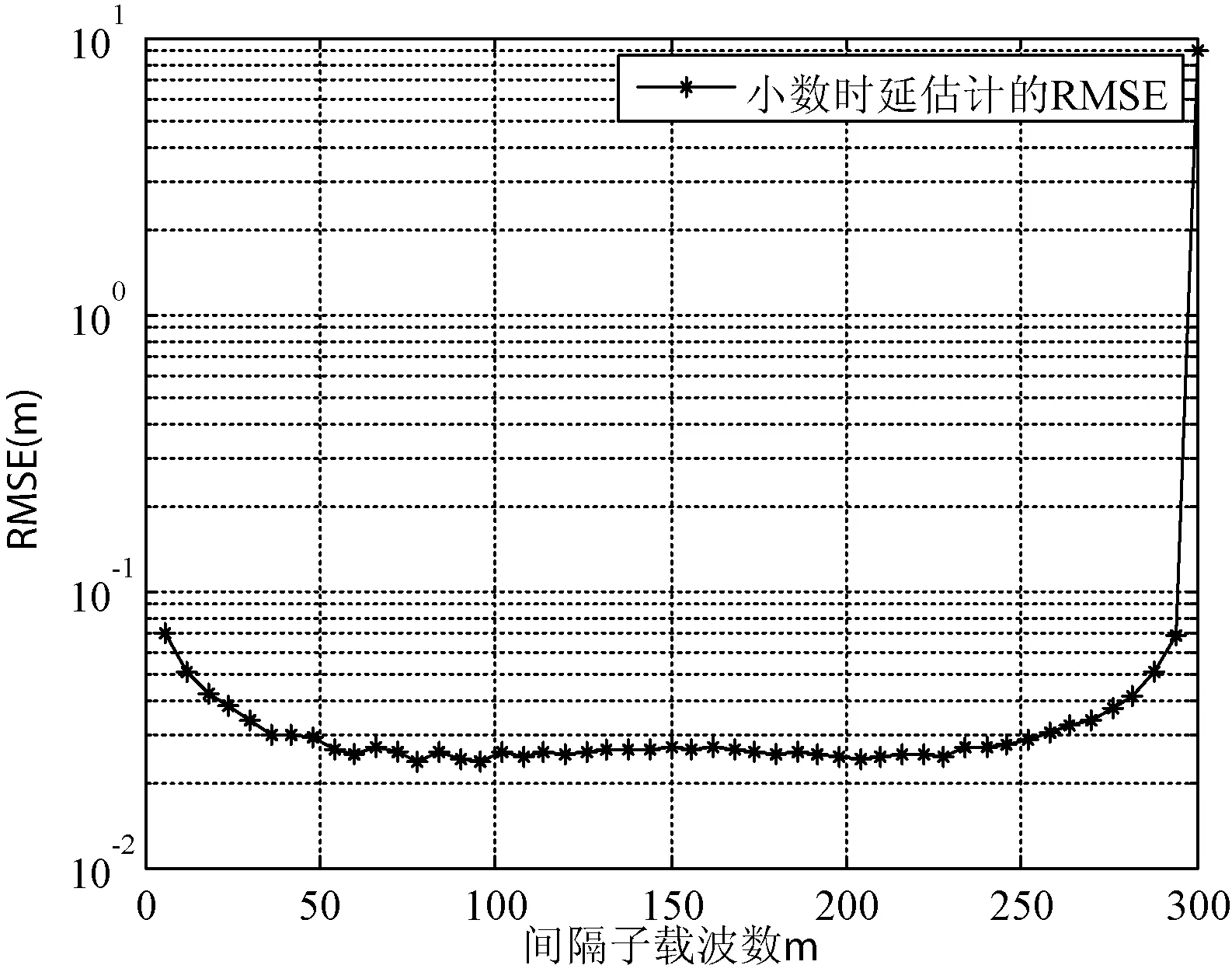
图8　信噪比为30 dB时，小数时延估计的RMSE随m值的变化曲线

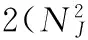
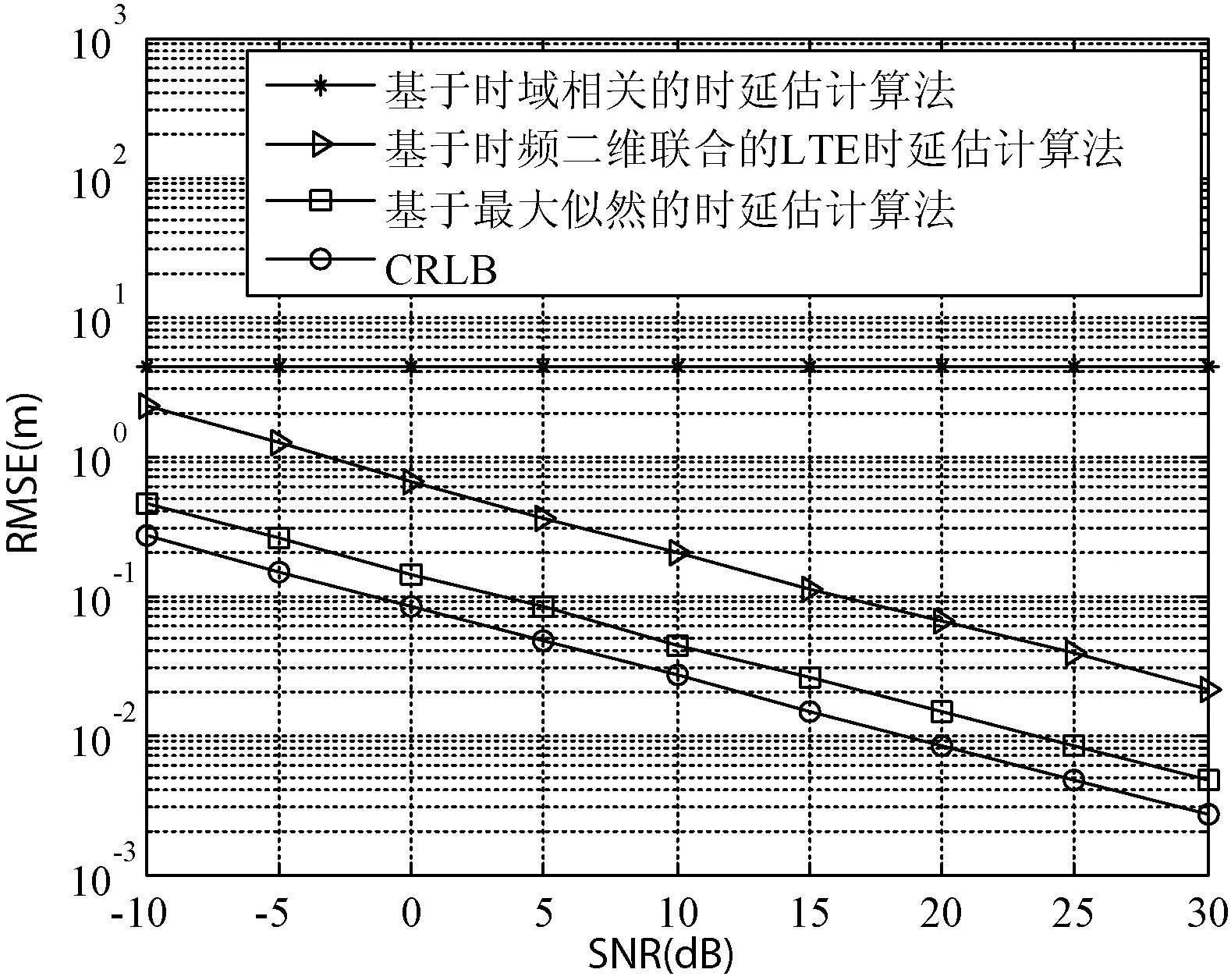
图9　三种算法的RMSE曲线

最后，图10给出在多径信道下本文算法的时延估计的RMSE曲线。仿真时采用1个PRS进行时延估计，间隔子载波数v等于204。以AWGN信道下的仿真结果作为参考，在AWGN信道下，该算法的测距精度在SNR=20 dB时约为0.1 m，在ITU-A信道下的精度约4 m。仿真结果表明，该算法在ITU-A信道下的性能明显差于AWGN信道下的性能。这是因为该算法利用子载波间的相位差估计小数时延，而多径会带来较大的相位误差，从而导致该算法在ITU-A信道下的性能明显下降。

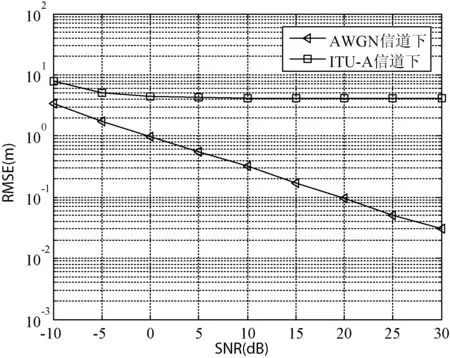
图10　在多径信道下的RMSE曲线

4结语

由于LTE PRS的时频结构特点会导致相关检测出现周期性峰值，若移动台与基站之间的距离较大时，则会出现测距模糊。本文提出一种基于LTE定位参考信号的时频二维联合时延估计算法。首先，在频域上以较大滑动步长对接收信号做滑动相关，快速找到OFDM符号的粗略起始时刻。然后利用本地定位参考信号与滑动窗内的接收信号做相关并提取整数倍传输时延。最后在频域上利用子载波间的相位差估计小数倍传输时延。仿真结果表明，该算法可以有效地解决了测距模糊问题，时延估计精度不受系统采样周期限制且计算复杂度低。

参考文献

[1] 唐科萍,许方恒,沈才樑.基于位置服务的研究综述[J].计算机应用研究,2013,29(12):4432-4436.

[2] Sesia S,Issam I,Baker M.LTE-The UMTS Long Term Evolution:From Theory to Practice[M].2nd ed.Wiley,2011.

[3] 3GPP TS 36.355 V11.1.0,LTE Positioning Protocol(LPP)[S].February 2013.

[4] Kim J,Kim S,Kim N Y,et al.A novel location finding system for 3GPP LTE[C]//2009 IEEE 20th International Symposium on Personal,Indoor and Mobile Radio Communications.Tokyo:IEEE,2009:3213-3217.

[5] 梁伟擘,彭建华.一种基于MIMO的时延估计算法[J].计算机工程,2014,40(1):107-112.

[6] del Peral-Rosado J A,López-Salcedo J A,Seco-Granados G,et al.Evaluation of the LTE positioning capabilities under typical multipath channels[C]//2012 6th Advanced Satellite Multimedia Systems Conference (ASMS) and 12th Signal Processing for Space Communications Workshop (SPSC).Baiona:IEEE,2012:139-146.

[7] Huang M,Xu W.Enhanced LTE TOA/OTDOA estimation with first arriving path detection[C]//Wireless Communications and Networking Conference (WCNC).Shanghai:IEEE,2013:3992-3997.

[8] Benedetto F,Giunta G,Guzzon E.Enhanced TOA-based indoor-positioning algorithm for mobile LTE cellular systems[C]//2011 8th Workshop on Positioning Navigation and Communication (WPNC). Dresden:IEEE,2011:137-142.

[9] 陈健.面向3GPP-LTE终端无线定位的参数估计与定位解算研究[D].成都:成都电子科技大学,2011.

[10] del Peral-Rosado J A,López-Salcedo J A,Seco-Granados G,et al.Joint maximum likelihood time-delay estimation for LTE positioning in multipath channels[J].EURASIP Journal on Advances in Signal Processing,2014(1):1-13.

[11] 3GPP TS 36.211 V11.1.0,Physical Channels and Modulation[S].February 2013.

[12] Kay S M,罗鹏飞.统计信号处理基础:估计与检测理论[M].北京:电子工业出版社,2003.

收稿日期：2015-01-19。国家自然科学基金项目(61172054，6136 2006)；广西自然科学基金项目(2014GXNSFAA118387，2013GXNSFAA 019334)；桂林电子科技大学研究生创新项目(GDYCS201409)。刘韦韦，硕士生，主研领域：LTE测距定位技术。林基明，教授。后茜，硕士生。丁进，硕士生。

中图分类号TP39

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.07.032

TIME-FREQUENCY 2D JOINT TIME DELAY ESTIMATION ALGORITHM BASED ON LTE POSITIONING REFERENCE SIGNALS

Liu WeiweiLin JimingHou QianDing Jin

(SchoolofInformationandCommunicationEngineering,GuilinUniversityofElectronicTechnology,Guilin541004,Guangxi,China)

AbstractThe feature of frequency domain comb structure of LTE positioning reference signal will generate periodic correlation peaks when the correlation detection is used in time domain. While the distance between mobile station and base station is far away, ranging ambiguity appears. In order to solve the problem, in this paper we propose a time-frequency two-dimensional joint time delay estimation algorithm, which is based on LTE positioning reference signals. First, the algorithm makes sliding correlation on the received signals with larger sliding step in frequency domain so as to find the rough start time of OFDM symbol quickly. Then it makes the correlation between the local positioning reference signals and the received signal and extracts integer multiple transmission delay. Finally, in frequency domain it uses the phase differences between subcarriers to estimate the decimal multiple transmission delay, therefore obtains accurate time delay estimation. Simulation results show that the algorithm can solve the ranging ambiguity problem effectively. Meanwhile its ranging accuracy is about four metres when the SNR is equal to 10 dB.

KeywordsLong-term evolutionPositioning reference signalRanging ambiguityTime-frequency two-dimensional jointTime delay estimation