高斯束叠前深度偏移影响因素分析

韩建光， 张晓波， 邢占涛， 陈　鹏， 王　赟， 于常青

(1.中国地质科学院 地质研究所，北京　100037；2.中国地质科学院，北京　100037；3.中国华电集团科学技术研究总院有限公司，北京　100160；4.成都理工大学　油气藏地质及开发工程国家重点实验室，成都　610059；5.中国地质大学　地球物理与信息技术学院，北京　100083)



高斯束叠前深度偏移影响因素分析

韩建光1， 张晓波2， 邢占涛3， 陈鹏4， 王赟5， 于常青1

(1.中国地质科学院 地质研究所，北京100037；2.中国地质科学院，北京100037；3.中国华电集团科学技术研究总院有限公司，北京100160；4.成都理工大学油气藏地质及开发工程国家重点实验室，成都610059；5.中国地质大学地球物理与信息技术学院，北京100083)

摘要：高斯束偏移方法是一种优秀的偏移算法，不仅具有接近于波动方程偏移方法的成像精度，而且保留了Kirchhoff偏移方法高效、灵活的优点。高斯束偏移成像效果以及计算效率受许多因素影响，这里以二维共炮域高斯束叠前深度偏移方法为基础，分析了初始束宽、成像角度及速度光滑程度对偏移效果和效率的影响机理，并通过洼陷模型、Marmousi模型以及Sigsbee 2B模型的偏移试算，对初始束宽、成像角度以及速度光滑程度对高斯束叠前深度偏移的影响进行了分析。

关键词：高斯束； 叠前深度偏移； 影响因素； 数值模型分析

0引言

高斯束方法将波动方程与射线理论相结合，同时考虑了波的运动学特征和动力学特征，通过运动学射线追踪获取射线路径，动力学追踪获取中心射线附近的能量分布。高斯束偏移方法是近年来发展的一种偏移算法，它不但克服了Kirchhoff 偏移方法无法解决的多值走时问题，同时保留了Kirchhoff偏移方法高效、灵活的优点，具有接近于波动方程偏移的成像精度[1]。

在地震学领域，利用高斯束方法进行波场计算[2-4]最早应用于地震波场的正演模拟[5-6]，之后一些国外学者对高斯束偏移进行了研究，Hill[7-8]先后提出了高斯束叠后偏移方法以及基于共偏移距道集的叠前深度偏移方法；Hale[9-10]详细介绍了高斯束偏移与Kirchhoff偏移以及倾斜叠加相比的优点，并给出了具体的计算公式以及优化算法，分析了高斯束偏移的计算效率；Gray[11-12]针对Hill方法对观测系统适应性不足，提出了共炮域的叠前偏移方法，并在以后的研究中基于单程波真振幅偏移理论，提出了真振幅高斯束偏移方法；Popov[13-14]提出了一种新的真振幅高斯束叠前深度偏移理论，对地下复杂地质构造获得了高质量的成像结果。

高斯束偏移是一种优秀的偏移算法，但实现过程比较复杂，需要一系列的数值计算方法以及优化算法[10]。此外高斯束偏移成像受许多因素影响，如初始束宽的大小、成像角度的控制以及速度模型的光滑程度等。这里从成像效果以及计算效率两个方面，通过不同的数值模型试算对其主要影响因素进行研究分析。

1高斯束方法原理

1.1基本原理

高斯束方法将波动方程与射线理论相结合，在射线中心坐标系下求解波动方程。二维各向同性介质中，中心射线坐标系下高斯束频率域的表达式为[2- 3]

1.2高斯束特点

高斯束是波动方程在射线坐标系下的高频近似解，具有波动方程的相关特性。与传统的射线方法不同，高斯束方法不仅在中心射线上有波场能量，而且可以计算射线周围的波场值，其形态受初始束宽和频率的影响。

图1为不同初始束宽高斯束在均匀介质中传播的瞬时波场图，介质中的波速为3 000 m/s，子波频率为25 Hz，初始束宽分别为150 m、260 m、340 m和500 m。从图1中可以看出，初始束宽的选取影响着波前面的形态。初始宽度越小，高斯束波前曲率变化剧烈，波场扩散越快；初始宽度越大，高斯束波前曲率变化较为平缓，波场扩散越慢。

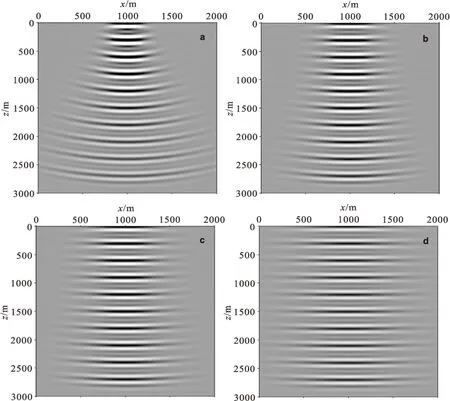
图1　初始束宽不同的高斯束在均匀介质中传播的瞬时波场图Fig．1　Gaussian beam wavefield in a homogeneous medium with different initial beam width(a)150 m ；(b)260 m ；(c)340 m ；(d)500 m

图2为不同频率高斯束在均匀介质中传播的瞬时波场图，高斯束的初始宽度相同，均为260 m，频率分别为20 Hz、25 Hz、30 Hz和40 Hz。从图2中可以看到，高斯束的波前曲率与频率无关，频率的大小影响着高斯束在中心射线周围能量的分布。

结果表明，频率越高高斯束能量越集中于中心射线附近，即频率越高沿垂直于中心射线方向衰减越快，高斯束的宽度越窄。

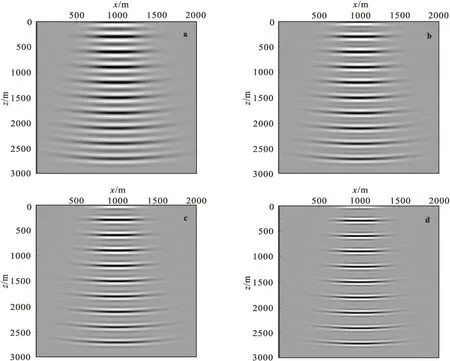
图2　不同频率的高斯束在均匀介质中传播的瞬时波场图Fig．2　Gaussian beam wavefield in a homogeneous medium with different frequencies(a)20 Hz ；(b)25 Hz ；(c)30 Hz ；(d)40 Hz

2高斯束叠前深度偏移原理

高斯束叠前偏移成像是由震源处正向延拓的波场与束中心点处反向延拓波场的互相关获得。在二维各向同性介质中，假设xs=(xs,0)和xr=(xr,0)分别为震源和接收点。根据Hill[8]提出的共偏移距域高斯束叠前偏移公式，给出了二维共炮域高斯束叠前偏移公式为式(2)。

(3)

式中：ωr为参考频率；L0表示高斯束的初始束宽；u(xr,xs,ω)为地震记录频谱。

用A、T分别表示高斯束的复振幅值和旅行时，则高斯束表达式可以表示为式(4)。

uGB(x,x0,p,ω)=Aexp(iωT)

(4)

将高斯束表达式(4)代入式(2)，则高斯束叠前深度偏移公式可以表示为式(5)。

(5)

(6)

3高斯束偏移影响因素分析

3.1初始束宽的影响

在进行高斯束偏移时，需要选取一系列的参数，如初始束宽L0、束中心间隔α、射线参数采样间隔Δp等。作为波动方程的高频渐进解，高斯束在传播路径上宽度越窄，其精度越高。但是如果初始宽度过小，高斯束在传播过程波场会迅速扩散，如图1所示。将每个束中心点附近的道集通过局部倾斜叠加分解为不同出射方向的局部平面波进行波场延拓，是高斯束偏移方法的核心算法之一，能够有效地减少计算量。在保证波场充分覆盖的前提下，适当地增大束中心间隔，可以提高偏移的计算效率。高斯束叠前偏移需要在震源和束中心点处分别以不同的射线参数出射高斯束进行波场计算，为了保证偏移成像的准确性，初始射线参数的间隔必须足够小以保证具有充足的射线覆盖。相比于束中心间隔，初始射线参数间隔的大小对高斯束偏移的计算时间有着显著的影响。因此，如何选取上述参数对高斯束偏移具有重要的影响。一般情况下可以参照Hill[7-8]所给定的选取准则

L0=2πVa/ωr

(7)

(8)

(9)

式中：Va为偏移速度的几何平均值；ωh为最高有效频率。初始束宽的大小决定束中心间隔和射线参数采样间隔的取值。

采用洼陷模型模拟数据对初始束宽，对高斯束

偏移的影响进行了测试，洼陷速度模型如图3所示。正演模拟采用有限差分方法，震源为30 Hz的Ricker子波，共81炮，炮间距为50 m，每炮301检波点双边接收，道间距为10 m，采样时间为2.6 s，采样间隔为2 ms。图4为初始束宽分别为100 m、200 m、300 m、500 m的洼陷模型偏移结果，从图4中可以看到，不同的初始束宽高斯束偏移成像结果基本相同。虽然初始束宽的选取对单一高斯束周围波场计算产生较大的影响，但高斯束偏移过程中通过高斯束叠加成像均可以得到准确的偏移结果，说明高斯束偏移方法对初始束宽大小不敏感。

图3　洼陷速度模型Fig．3　Sag velocity model

图4　不同初始宽度的洼陷模型高斯束叠前深度偏移结果Fig．4　Gaussian beam prestack depth migration results with different initial beam width(a)初始束宽为 100 m的成像结果；(b)初始束宽为 200 m的成像结果；(c)初始束宽为300 m的成像结果；(d)初始束宽为500 m的成像结果

通过模型试验可知，高斯束偏移的成像效果对初始宽度的大小并不是特别的敏感，只要给定的初始束宽值与式(7)计算得到的值相差不大，基本都可以得到较为理想的成像结果。但是由于初始束宽的变化导致束中心间隔和射线参数采样间隔不同，对计算效率产生一定的影响。因此，可以在保证偏移精度不受影响的前提下，适当的调整上面的参数，以提高偏移计算效率。

3.2成像角度的影响

除了上述参数之外，成像角度的控制也是影响高斯束偏移的重要因素。成像角度过大可能会导致不必要的偏移噪音，而且需要花费更多的计算时间,成像角度过小会限制某些陡倾构造的成像。

作者通过对Marmousi模型的试算，分析了不同成像角度对高斯束偏移成像的影响，Marmousi速度模型如图5所示。正演记录共240 炮，炮间距为25 m，每炮96 道，道间距为25 m，最小偏移距为200 m，时间采样间隔为4 ms，采样点数为750。图6(a)和图6(b)分别为最大成像角度为100°和150°时的高斯束叠前深度偏移成像结果。从图6可以看出，对于最大成像角度为100°时所得到的偏移结果，由于受成像角度限制，断层附近的陡倾构造未能成像(矩形所示部分)。而当最大成像角度为150°时，断层附近陡倾构造获得较好的成像，高斯束偏移准确地恢复了模型复杂的构造形态。通过Marmousi模型测试可知，成像角度的控制对于高斯束叠前深度偏移具有较大的影响，可以根据偏移的需要，适当地调整成像角度的大小。对于存在陡倾构造的模型，可以适当增大成像角度，以保证陡倾构造能够获得成像。

图5　Marmousi速度模型Fig．5　Marmousi velocity model

图6　不同成像角度的Marmousi模型高斯束叠前深度偏移结果Fig．6　Gaussian beam prestack depth migration results with different imaging angle(a)最大成像角度为100°的成像结果；(b)最大成像角度为150°的成像结果

3.3速度光滑的影响

高斯束叠前深度偏移方法的关键，在于运动学射线追踪和动力学射线追踪。射线理论是地震波场的一种高频近似，其应用前提条件需满足地震波速度在一个波长范围内的相对变化很小，而实际的速度模型可能具有不连续的速度突变点、间断面或很强的速度梯度。为了满足射线理论的应用前提，需要对速度模型进行光滑处理以减小速度的相对变化，以保证射线追踪的可行性和有效性。因此，速度模型的光滑处理，对基于射线理论的高斯束叠前深度偏移具有较大影响。

通过对Sigsbee 2B模型试算分析速度光滑处理对高斯束偏移成像效果的影响。Sigsbee 2B层速度模型如图7(a)所示，模型中包含盐丘、断层以及绕射体等复杂构造，图7(b)为Sigsbee 2B偏移速度模型。图8(a)和图8(b)分别为采用原始速度以及速度光滑模型偏移得到的成像结果。从图8中可以看到，采用原始速度进行高斯束偏移，由于盐丘构造内部速度与周围速度差异较大，射线很难穿过高速盐丘体，导致盐丘体下部边界未能成像。而速度模型进行光滑处理之后再进行偏移成像，盐丘构造下部界面取得了较好的聚焦成像，模型整体的成像效果有了明显的提高。通过Sigsbee 2B模型测试可知，对速度模型进行适当的光滑处理，可以明显的改善高斯束偏移成像效果。

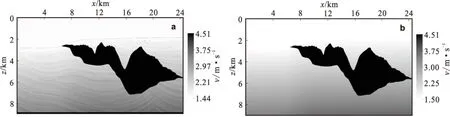
图7　Sigsbee 2B速度模型Fig．7　Sigsbee 2B velocity model(a)层速度模型；(b)偏移速度模型

图8　Sigsbee 2B模型高斯束叠前深度偏移结果Fig．8　Gaussian beam prestack depth migration results of Sigsbee 2B model(a)原始速度模型高斯束偏移成像结果；(b)速度光滑模型高斯束偏移成像结果

4结论

高斯束偏移成像效果以及计算效率受许多因素影响，作者分别通过洼陷模型、Marmousi模型以及Sigsbee 2B模型的偏移试算，系统地分析了初始束宽、成像角度以及速度光滑对高斯束叠前深度偏移的影响。虽然初始束宽的大小对高斯束偏移成像质量影响不大，但初始束宽的大小决定束中心间隔和射线参数采样间隔的取值，因此对计算效率产生较大的影响。成像角度对高斯束叠前深度偏移具有较大的影响，成像角度过大可能会导致不必要的偏移噪音，而且需要花费更多的计算时间；成像角度过小会导致某些陡倾构造无法成像。因此，需要综合考虑高斯束偏移的成像效果和计算效率，适当地调整上面的参数。此外，速度光滑处理可以减小速度模型的相对变化，保证射线追踪的可行性和有效性，对高斯束叠前深度偏移质量有较大的影响，因此在高斯束偏移过程中应对速度模型进行适当的光滑处理。

参考文献：

[1]岳玉波，李振春，钱忠平，等．复杂地表条件下保幅高斯束偏移[J]．地球物理学报，2012，55(4)：1376-1383.

YUE Y B,LI Z C,QIAN Z P,et al.Amplitude-preserved Gaussian beam migration under complex topographic conditions[J].Chinese Journal of Geophysics,2012,55(4):1376-1383.(In Chinese)

[4]Popov M M.A new method of computation of wave fields using Gaussian beams[J].Wave Motion,1982(4):85-97.

[6]NOWACK R L.Calculation of Synthetic Seismograms with Gaussian Beams[J].Pure and Applied Geophysics,2003,160:487-507.

[7]HILL N R.Gaussian beam migration[J].Geophysics,1990,55:1416-1428.

[8]HILL N R.Prestack Gaussian-beam depth migration[J].Geophysics,2001,66:1240-1250.

[9]HALE D.Migration by the Kirchhoff,slant stack and Gaussian beam methods[R].Colorado:CWP Annual Project Review Meeting,1992.

[10]HALE D. Computational aspects of Gaussian beam migration[R].Colorado:CWP Annual Project Review Meeting,1992.

[11]GRAY S H.Gaussian beam migration of common-shot records[J].Geophysics, 2005,70(4):S71-S77.

[12]GRAY S H,BLEISTEIN N.True-amplitude Gaussian-beam migration[J].Geophysics,2009,74(2):S11-S23.

[13]POPOV M M,SEMTCHENOK N M,POPOV P M,et al.Reverse time migration with Gaussian beams and velocity analysis applications[J].Extended Abstracts of 70thAnnual Internat EAGE Mtg,2008：F048.

[14]POPOV M M,SEMTCHENOK N M,POPOV P M,et al.Depth migration by the Gaussian beam summation method[J].Geophysics, 2010,75(2):S81-S93.

收稿日期：2015-04-09改回日期：2015-08-03

基金项目:国家自然科学基金项目(41425017，41374131，41374128)；科技部863课题(2013AA064201)

作者简介：韩建光(1987-)，男，博士，主要从事地震偏移成像与多分量地震技术研究,E-mail:hanjianguang613@163.com。

文章编号：1001-1749(2016)03-0403-07

中图分类号：P 631.4

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.03.17

The analysis on influence factors of imaging precision in Gaussian beam prestack depth migration

HAN Jian-guang1, ZHANG Xiao-bo2, XING Zhan-tao3,CHEN Peng4, WANG Yun5, YU Chang-qing1

(1.Institute of Geology,Chinese Academy of Geological Sciences,Beijing100037,China;2.Chinese Academy of Geological Sciences,Beijing100037,China;3.China Huadian Science and Technology Institute,Beijing100160,China;4.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation Chengdu University of Technology,Chengdu610059,China；5.School of Geophysics and Information Technology,China University of Geoscience,Beijing100083,China)

Abstract:Gaussian beam migration is an elegant and efficient depth migration method with accuracy comparable to wave-equation migration and efficiency and flexibility comparable to Kirchhoff migration. Gaussian beam migration imaging quality and computation efficiency is influenced by many factors. In this paper, based on Gaussian beam prestack depth migration algorithm of common-shot records in two-dimensional media, the influence mechanism of the initial beam width, imaging angle and velocity smooth on effectiveness and efficiency of migration are studied. Finally, the effects of the initial beam width, imaging angle and velocity smooth on Gaussian beam prestack depth migration are studied by testing of sub-sag model, Marmousi model and Sigsbee 2B model.

Key words:Gaussian beam; prestack depth migration; influence factor; numerical model analysis