二维层状VTI介质试射射线追踪方法

李永博， 吴　琼， 王大勇， 李庆春， 李建国

(1.中国地质科学院　地球物理地球化学勘查研究所,廊坊　065000；2.长安大学　地质工程与测绘学院,西安　710054;3.东方地球物理公司　新兴物探开发处，涿州　072751)



二维层状VTI介质试射射线追踪方法

李永博1， 吴琼1， 王大勇1， 李庆春2， 李建国3

(1.中国地质科学院地球物理地球化学勘查研究所,廊坊065000；2.长安大学地质工程与测绘学院,西安710054;3.东方地球物理公司新兴物探开发处，涿州072751)

摘要：地震波场正演模拟是研究地震波传播规律的有效手段，为地震勘探提供基本的理论依据。为提高地震勘探的精度及勘探能力，研究复杂介质中地震波传播问题显得尤为重要。针对各向异性介质中的地震波场正演问题，基于各向异性介质和试射射线追踪方法的基本理论，分析了横向各向同性(VTI)介质中存在的群相关系，研究了VTI介质中的Snell定律及角度转换关系，并引入了透射系数和反射系数，具体讨论了试射射线追踪算法，通过数值模拟实现了地震波场正演，客观合理地模拟了地震波在VTI介质中的传播。

关键词：波场正演； 横向各向同性介质； 射线追踪

0引言

地震波场正演模拟，为地震勘探提供了重要的理论基础。常规的地震勘探方法几乎都是以均匀介质模型为假设前提，然而地下介质基本上都是各向异性的，这使地震波的传播更加复杂多变[1-2]。因此，研究地震波在各向异性介质中的传播规律就显得尤为重要[4]。

常见的地震波场正演方法包含射线追踪法和波动方程法，其中射线追踪方法是一种快速有效的地震波场正演模拟方法。20世纪80年代末以来，随着Kirchhoff积分叠前深度偏移方法的成功运用，作为其基础算法之一的射线追踪方法也得到了很大的推进和发展[3]。随后，国内、外学者不断将各向同性介质中的射线追踪方法引入到各向异性介质中，并加以研究和发展，使各向异性介质中的射线追踪方法日臻完善[4-8,11-16]。

VTI(Vertical Transversely Isotropy)介质是一种常见的各向异性介质，是典型的具有垂向对称轴的横向各向同性介质[8]。在VTI介质中，地震波的传播速度及透反射的能量分配受到介质各向异性的影响发生变化。因此，研究VTI介质射线追踪方法对解决介质的各向异性问题具有重要意义。这里采用经典的试射射线追踪方法对VTI介质进行正演试算，并引入透反射系数计算地震波的能量分配。

1方法原理

研究各向异性介质，首先要确定介质的各向异性参数和弹性参数的对应关系，这样才有利于正确分析各向异性介质中影响地震波传播的因素，进而进行正演模拟及数据处理等研究。VTI介质的各向异性性质可以用Thomsen参数[11]或弹性系数来表示，但后者的物理意义相对不明确。因此，这里采用Thomsen参数来描述VTI介质的各向异性性质。

1.1群相关系

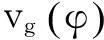
图1　各向异性介质中群相关系示意图Fig．1　The group-phase relations in 　　　　　　　VTI media

根据介质弱各向异性的假设，给出弱各向异性介质中P波和SV波相速度的表达式[11]：

(1)

式中：vp0为P波的垂直速度；vS0为S波的垂直速度；ε表示P波各向异性程度；δ表示P波和S波的变异系数，ε、δ为Thomsen参数。

Berryman[17]给出了由相速度转化为群速度的表达式，如式(2)所示。

(2)

Byun[18]给出了一种计算相速度的表达式，见式(3)。

(3)

由式(3)推导出相角和群角存在如下关系：

(4)

将式(2)代入式(4)可得到关系式，如式(5)所示。

(5)

赵爱华等[9]推导并验证了弱各向异性介质中由群角转换为相角的表达式：

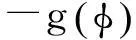
(6)

1.2透射与反射

由于VTI介质的对称轴是垂向的，故Snell定律可表达为[6]：

(7)

式中：P为射线参数；α为入射角。

VTI介质中透反射的角度关系如图2所示[8]，图2中αinc、αtra、αref分别表示波矢量入射角、透射角、反射角，φinc、φtra、φref分别表示射线入射角、透射角、反射角，θinc、θtra、θref分别表示波矢量入射相角、透射相角、反射相角，αdip为界面倾角。

李建国等[8]归纳推导并归纳了VTI介质中透反射的角度关系，即：

(8)

Ruger[19]给出了VTI介质透反射系数的近似公式，各向异性介质中的透反射系数包括各向同性项和各向异性项两部分。以P波为例，VTI介质中PP波反射系数近似解表示为RPP，其各向同性项和各向异性项分别表示为RiPP、RaPP，则：

RPP(θ)=RiPP(θ)+RaPP(θ)

(9)

式中，各向同性项为：

各向异性项为：

2试射射线追踪关键技术

试射法是一种经典的传统的两点间射线追踪方法，即给定震源和接收点位置，根据Snell定律调整从震源出发的射线直至收敛到接收点。

VTI介质试射法射线追踪的算法流程示意图如图3所示。其中，VTI介质射线追踪实现过程中，由入射射线计算透反射射线是整个算法的核心。

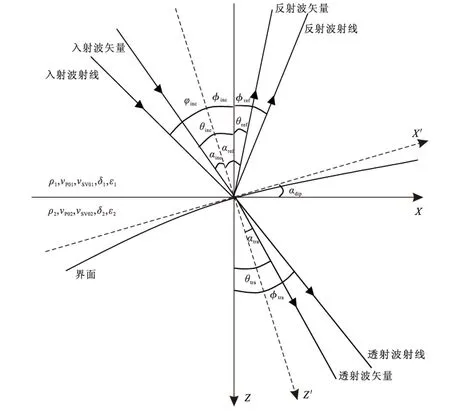
图2　VTI介质中透反射示意图Fig．1　The transmission and reflection in VTI media

以P波入射为例，射线及角度关系如图2所示，详细讨论VTI介质中由入射射线计算反射射线的实现过程。

图3　VTI介质试射射线追踪算法流程示意图Fig．3　Flow chart of shooting ray-tracing 　　　　　algorithm in VTI media

1) 给定P波初始射线入射角φinc，根据式(6)将φinc转化为波矢量入射角θinc。

2) 将θinc分别代入式(1)和式(8)计算P波相速度vP1及入射角αinc，则由式(7)可得反射点的射线参数p为式(10)。

(10)

3) 当P波入射发生反射时，满足Snell定律为：

(11)

对于PP反射波, 反射波矢量的相角θref满足方程：

(12)

求解方程(12)，得到θref。

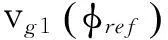
(13)

VTI介质中，计算PP透射波、PSV反射波及PSV透射波的思路与计算PP反射波的思路一致。

在建模方面，针对VTI介质结构特点，作者采用层状建模的方法，并对连续性不同的界面采用相应的拟合方法，对光滑连续的界面采用多项式拟合，对含间断点的线性界面(如断层)采用分段线性拟合。

3模型试算

3.1水平层状模型

水平层状VTI介质的模型示意图及参数如图4(a)所示。

由图4(b)可以看出，VTI介质试射射线追踪法与波动方程有限差分法计算的PP波旅行时相对误差不超过1.2 %，两者的相对误差随着炮检距的增大而减小，这是由于波动方程有限差分法的误差主要分布在炮点附近且计算精度受网格大小的影响；由图4(c)、图4(d)可知，两种方法得到的单炮记录中PP反射波基本一致，综上可知，VTI介质试射射线追踪是正确、可行、有效的。

3.2断层模型

VTI介质断层模型示意图及参数如图5所示，断层模型的横纵向断距均为100 m。

图4　VTI介质射线追踪法与波动方程法对比Fig．4　Comparison between and shooting ray-tracing method and wave equation method in VTI media(a) 模型示意图及参数(参数来自文献[4])；(b) 试射法与波动方程法PP波旅行时相对误差；(c) 试射射线追踪PP波单炮记录；(d) 波动方程法单炮记录(数值模拟来自文献[10]的程序)

由图6可知，断层的PSV反射波的射线路径及合成记录上出现盲区，断层上下盘的反射清晰，且炮集记录中出现断面反射，说明试射法数值模拟结果能够正确反映断层的形态，由此可见，VTI介质试射射线追踪对二维间断界面模型是有效的。

3.3透镜体模型

VTI介质透镜体模型示意图及参数如图7所示，透镜体深度范围为350 m～450 m。

由图8可以看出，透镜体顶面和底面的PP反射波射线路径及合成记录的清晰可见，底面PP反射波的极性受到各向异性的影响发生变化，且在合成记录上能够较容易分辨出透镜体的形态。结果表明，VTI介质试射射线追踪对较为复杂的起伏模型是可行的。

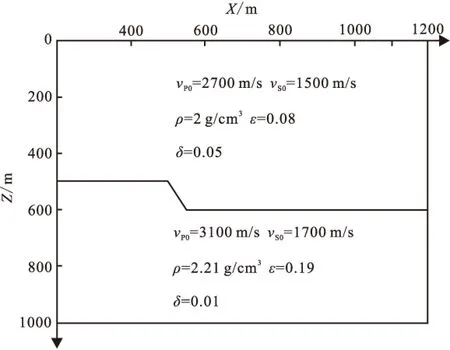
图5　模型示意图及参数Fig．5　Model diagram and parameters

4结论

试射法是一种经典的射线追踪方法，通过对VTI介质的正演模拟，得到以下结论：

1)归纳总结了VTI介质速度及角度的表达式及群相转化公式，并给出了VTI介质试射射线追踪算法中由入射射线计算透射和反射射线的具体实现方法。

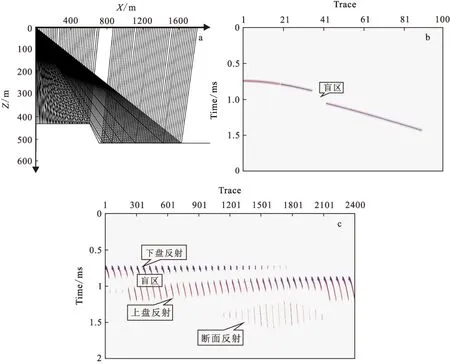
图6　断层模型PSV波射线追踪Fig．6　Result of fault model PSV wave ray tracing(a) PSV波单炮射线路径；(b) PSV波单炮记录；(c) PSV波炮集记录

图7　模型示意图及参数Fig．7　Model diagram and parameters

2)在VTI介质射线追踪过程中加入透反射系数的计算，改善了大多数各向异性介质射线追踪方法不考虑能量分配的问题。

3)通过模型试算可知，VTI介质试射射线追踪方法是可行有效的。对起伏界面和间断界面模型，VTI射线追踪都能够较准确反映界面的形态和介质结构。同时，程序能够实现初至波、PP波及PSV波的单一波或多波组合的正演模拟。由于建模方法，作者提出的正演模拟对复杂模型还有一定的局限性，有待进一步改进。此外，该射线追踪方法可推广至其他各项异性介质(如HTI介质)及三维正演模拟。

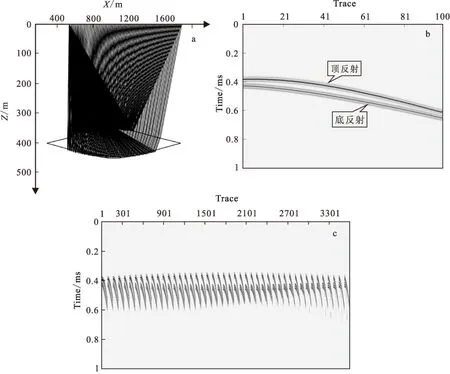
图8　透镜体模型PP波射线追踪Fig．8　Result of lens model PP wave ray tracing (a) PP波单炮射线路径；(b) PP波单炮记录；(c) PP波炮集记录

参考文献：

[1]滕吉文,张中杰,王爱武,等.弹性介质各向异性研究沿革现状与问题[J].地球物理学进展,1992,7(4):14-28.

TENG J W,ZHANG Z J,WANG A W,et al.The study of anisotropy in elastic medium:evolution,present situation and questions[J].Progress in Geophysics,1992,7(4):14-28.(In Chinese)

[2]张中杰.地震各向异性研究进展[J].地球物理学进展,2002,17(2):281-293.

ZHANG Z J.A review of the seismic anisotropy and its applications[J].Progress in Geophysics, 2002,17(2):281-293.(In Chinese)

[3]高尔根,徐果明,赵燚.一种任意界面的逐段迭代射线追踪方法[J].石油地球物理勘探,1998,33(1):54-60.

GAO E G,XU G M,ZHAO Y.Segmentally-iterative ray tracing method for any interface[J].OGP,1998,33(1):54-60.(In Chinese)

[4]孔选林,李录明,罗省贤,等.各向异性介质中地震波射线正演[J].物探化探计算技术,2008,30(3):178-184.

KONG X L,LI L M,LUO S X,et al.Seismic wave ray forward in anisotropic medium[J].Computing Techniques for Geophysical and Geochemical Exploration,2008,30(3):178-184.(In Chinese)

[5]张文生,何樵登,朱建伟,等.横向各向同性介质中群速度的计算[J].物探化探计算技术,1997,19(2):97-102.

ZHANG W S,HE J D,ZHU J W,et al.Calculation of group velocity in transversely isotropic media[J].Computing Techniques for Geophysical and Geochemical Exploration,1997,19(2):97-102. (In Chinese)

[6]邓怀群,刘雯林,赵正茂.横向各向同性介质中纵波和转换横波的快速射线追踪方法[J].石油物探,2000,39(4):1-11.

DENG H Q,LIU W L,ZHAO Z M.Fast ray-tracing method for compressional and converted waves in transversely isotropic media[J].GPP,2000,39(4):1-11.(In Chinese)

[7]赵爱华,张美根,丁志峰.横向各向同性介质中地震波走时模拟[J].地球物理学报,2006,49(6):1762-1769.

ZHAO A H,ZHANG M G,DING Z F.Seismic traveltime computation for transversely isotropic media[J].Chinese J.Geophys,2006,49(6):1762-1769.(In Chinese)

[8]李建国,李彦鹏,郭晓玲.VTI介质试射射线追踪[J].石油地球物理勘探,2010,45(4):491-496.

LI J G,LI Y P,GUO X L.VTI medium test-firing ray tracing[J].OGP,2010,45(4):491-496.(In Chinese)

[9]赵爱华,丁志峰.一种弱各向异性介质地震波群速度的近似表示新方法[J].地球物理学进展,2005,20(4):916-919.

ZHAO A H,DING Z F.New approximate expressions of Seismic group velocities for weakly anisotropic media[J].Progress in Geophysics,2005,20(4):916-919.(In Chinese)

[10]周学明.交错网格高阶差分数值模拟及叠前逆时偏移[D].西安:长安大学,2010.

ZHOU X M.Staggered-grid High-order Finite-difference Numerical Simulation and Prestack Reverse-time Migration[D].Xi’an:Chang’an University,2010.(In Chinese)

[11]THOMSEN L.Weak elastic anisotropy[J].Geophysics,1986,51(10):1954-1966.

[12]GAJEWSKI D.PSENCIK I.Computation of high-frequency seismic wavefields in 3-D laterrally inhomogeneous anisotropic media[J].Geophys.J.R.astro.,1987,91:383-411.

[13]GRECHKA V.Y.MCMECHAN G.A.3-D two-point ray tracing for heterogeneous,weakly transversely isotropic media[J].Geophysics,1996,61(6):1883-1894.

[15]ROGISTER Y.SLAWINSKI M.A.Analytic solution of raytracing equations for a linearly inhomogeneous and elliptically anisotropic velocity model[J].Geophysics,2005,70(5):37-41.

[16]DEHGHAN K.FARRA V.NICOLETIS L.Approximate ray tracing for qP-waves in inhomogeneous layered media with weak structural[J].Geophysics,2007,72(5):35-46.

[17]BERRYMAN J.G.Long-wave elastic anisotropy in transversely isotropic media[J].Geophysics,l979,44:896-917.

[18]BYUN B.S..Seismic parameters for transversely isotropic media[J].Geophysics,1984,49(11):1908-1914.

[19]RUGER A.P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry[J].Geophysics,1997,62:713-722.

收稿日期：2015-03-13改回日期：2015-06-23

基金项目:国家自然科学基金(41374145,41304105)

作者简介：李永博(1986-)，男，硕士，主要研究方向为地震勘探和电磁法勘探，E-mail:liyongbo@igge.cn。

文章编号：1001-1749(2016)03-0396-07

中图分类号：P 631.4

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.03.16

Shooting ray tracing in 2-D VTI media

LI Yong-bo1, WU Qiong1, WANG Da-yong1, LI Qing-chun2, LI Jian-guo3

(1. Institute of Geophysical and Geochemical Exploration, CAGS, Langfang065000, China;2. College of Geology Engineering and Geomatics, Chang'an University, Xi’an710054, China；3.Bureau of Geophysical prospecting,Zhuozhou072751,China)

Abstract:Seismic wave numerical simulation is an effective measure to study seismic wave propagation, and it provides theoretical basis for seismic exploration. In order to improve the precision and ability of seismic exploration, it is particularly important to research seismic wave propagation in complex media. According to the seismic forward modeling in anisotropic media, from the theories of anisotropic media and shooting ray-tracing method, and on the basis of existing studies, the group-phase relations of velocity and angle are analyzed respectively in vertical transversely isotropic (VTI) media. Then the Snell theorem and the angular relation are studied in VTI media, and both the reflection coefficient and the transmission coefficient are brought in. The shooting ray-tracing algorithm is discussed specifically, and the seismic forward modeling is achieved by numerical simulation, which can simulate the seismic wave propagation more objectively and reasonably in anisotropic media.

Key words:numerical simulation; VTI; ray tracing