基于改进粒子群算法的叠前弹性阻抗反演

张　进, 陈晓琦, 邢　磊, 安玲芳, 赵　玺, 安振芳

(中国海洋大学　海底科学与探测技术教育部重点实验室，青岛　266100)



基于改进粒子群算法的叠前弹性阻抗反演

张进, 陈晓琦, 邢磊, 安玲芳, 赵玺, 安振芳

(中国海洋大学海底科学与探测技术教育部重点实验室，青岛266100)

摘要：弹性阻抗反演是结合声阻抗反演与AVO反演的叠前地震反演技术，能够克服叠后波阻抗反演的缺陷，反映振幅随偏移距变化的信息，已经广泛应用于地震岩性识别和流体特征的获取。常规的线性迭代弹性阻抗反演方法存在依赖初始模型、容易陷入局部极值等缺陷。针对这一问题，提出了一种基于改进粒子群算法的弹性阻抗非线性反演方法，并利用该算法对胜利油田某工区地震资料进行了弹性阻抗反演，获得了多个弹性参数剖面，与实际钻井结果相符，该方法为复杂油气藏的勘探开发提供了一种有效可行的途径。

关键词：弹性阻抗反演； 粒子群算法； 非线性反演

0引言

常规叠后波阻抗反演技术基于地震波垂直入射的假设，其得到的反射振幅为共中心点道集叠加平均的结果，故不能反映反射振幅随炮检距或入射角的变化。为获取潜在的AVO效应，Connolly[1]将纵波反射系数随炮检距的变化引入地震道正、反演问题中，为孔隙流体和岩性识别提出了弹性阻抗EI(Elastic Impedance)的概念，能够提供振幅随着偏移距变化的信息，解决了在较大炮间距入射角情况下的纵波正、反演问题，具有足够的精度和良好的保真性，从EI提出至今，弹性阻抗反演取得了突破性的发展；Cambois[2]对AVO反演和弹性波阻抗(EI)反演方法进行了比较，得出弹性阻抗的反演结果更理想，在抗噪能力方面比AVO反演更有优势；Mallick等[3]讨论了Connolly弹性阻抗公式的应用及限制条件；Whitcombe D N[4]引入纵波速度、横波速度、密度三个参量，对Connolly提出的弹性阻抗进行了归一化；Whitcombe 等[5]在前人对于流体因子和岩性预测等方面研究成果的基础上，提出扩充弹性波阻抗(EEI)，可用于岩性和流体预测的;马劲风[6]基于Subhashis Mallick[7]和Yanghua Wang[8]提出了广义弹性阻抗(GEI)的概念，并给出使用弹性模量表示的Zoeppritz 方程的简化公式；倪逸[9]通过对目前几种弹性波阻抗计算方法的分析，提出了一种基于范数动态可调的改进方法；印兴耀等[10]提出利用Connolly弹性阻抗方程从三个角度反演结果中提取纵、横波速度和密度参数的方法，可以对地下储层的展布及含油气性进行预测；王保丽等[11]提出了一种新的基于佐普里兹Gary近似方程的弹性阻抗反演公式，能够减小间接计算产生的累计误差。

常用的反演方法一般为局部线性迭代方法或者将非线性问题线性化，具有依赖初始值、易陷入局部极值的缺陷。对于精度要求较高的EI反演来说，采用非线性优化方法，其解的性质、状态均有良好的表现。近年来，一些全局优化特性并且通用性好的搜索算法(如遗传算法、模拟退火算法、粒子群算法、人工神经网络算法等)，已经广泛应用在地震反演中。其中，粒子群算法对初始模型的依赖性小，参数设置少，收敛速度快，能够保证地震资料反演结果的精度。这里在基本粒子群算法中加入模拟退火算子用于反演弹性阻抗，通过对理论模型的分析和实际地震资料的反演，证明该方法的合理性和有效性。

1弹性阻抗的基本原理

与AVO的理论基础相同，弹性阻抗是基于平面波在两种半无限空间弹性介质分界面上的反射和透射所满足的Zoeppritz方程及其不同简化形式，是声阻抗(Acoustic impedance, AI)的推广。声阻抗表示入射角为零时的特例，而弹性阻抗是关于入射角的函数，可以标定和反演非零偏移数据体，其精度已经在广泛的应用中得到证明。

Connolly根据Zoeppritz方程的三项Aki & Richards简化公式推导出含有纵、横波速度、密度和入射角参数的弹性阻抗公式，如式(1)所示。

(2)

常规弹性阻抗反演流程如图1所示。

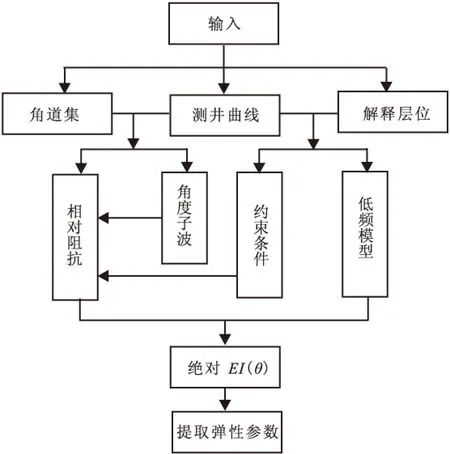
图1　弹性阻抗反演流程示意图Fig．1　The procedures of elastic impedance inversion

反演步骤为：

1)由于EI是关于纵、横波速度，密度和入射角的函数，在反演之前需要将地震数据的偏移数据体转化为角度数据体。

2)根据测井曲线或者岩心数据，计算出井旁道EI伪测井曲线。

3)角度子波的提取。子波提取是地震反演的关键之一，可直接影响反演精度，在提取之前要先对多口井的测井曲线进行层位标定。

4)对控制点上的EI曲线进行内插，利用角道集部分叠加资料与井旁道相应入射角的弹性阻抗建立波阻抗剖面的低频模型，进行低频成分的补充。

5)用非线性反演方法计算带限的弹性阻抗剖面，将低频模型的弹性波阻抗与带限的弹性波阻抗剖面融合，最终可以获得与实际情况相符合的弹性波阻抗剖面。

在得到不同角度下的弹性阻抗之后，可根据变换后的Connolly方程反演得到纵波速度Vp、横波速度Vs、密度ρ等岩性参数：

(3)

与声阻抗AI相比，弹性阻抗不存在声阻抗垂直入射的前提，能够克服由于叠加导致的有效信息损失的缺陷，并且EI由于含有AVO信息，其对油气饱和度更为敏感，故可以更全面、直观地反应与油气相关的信息，为油气藏的识别提供依据，降低油气检测的多解性。

地震资料的弹性阻抗反演实际上是一个最优化求解的非线性问题[12]，常规的线性算法虽收敛速度快，但易陷入局部最优。粒子群算法是一种基于迭代的优化工具，具有较强的搜索能力，容易理解，易于实现，近年来在模式分类、函数寻优、系统控制、以及工程应用等多个领域得到了成功地应用[13]。作者尝试在基本粒子群算法中加入模拟退火算子，并用其进行弹性阻抗的反演，取得了良好的效果。

2粒子群算法

2.1基本粒子群算法

粒子群算法(Particle Swarm Optimization，PSO)来源于鸟群和鱼群的群体运动行为，最早由Kennedy博士和Eberhart博士[14-15]提出，其数学描述如下：

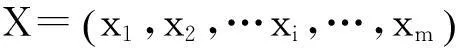
vid(t+1)=wvid(t)+c1r1(pid(t)-xid(t))+

c2r2(gd(t)-xid(t))

(4)

1≤i≤m1≤d≤n

(5)

其中：w为惯性权重因子；c1和c2为加速因子，均为正常数，c1为调节使粒子飞向自身最好位置方向的步长，c2为调节粒子飞向全局最好位置的步长；t是当前迭代次数；r1、r2是[0,1]内的随机数。

(6)

可设定上限速度Vmax来确保粒子不会由于速度过大而错过最优解，根据式(6)对粒子的速度进行限制，随机产生粒子的速度和初始位置，然后按照式(4)、式(5)进行迭代，直到找到符合条件的解。粒子群算法实现方便、收敛速度快，参数设置少，是一种高效的搜索方法，但“早熟”收敛和易陷入局部极值是其最主要的缺点。

2.2加入模拟退火算子的随机粒子群算法

在上述的基本粒子群算法中，当w=0，粒子的进化方程就变为式(7)。

(7)

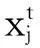
(8)

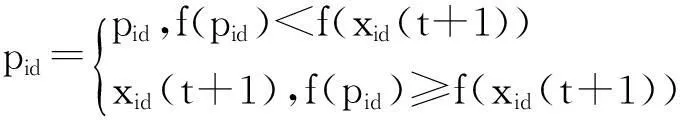
(9)

(10)

(11)

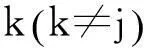
为使粒子j以较大概率趋于最优解，作者提出加入模拟退火算子的随机粒子群算法(ASPSO)：以当前历史最优位置gd为初始状态，选取初始温度T=T0，采用经典退火过程Tk=akT0，根据公式(12)产生下一个状态：

(12)

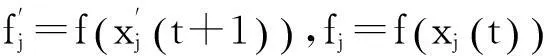
(13)

模拟退火方法本身具有很好的全局收敛性，因而采用该方法生成微粒j并根据式(12)、式(13)进行状态更新，不会对随机粒子群算法的全局收敛性产生负面影响。

2.3改进粒子群算法性能测试

为了检测粒子全优化算法的性能，用Generalized Rastrigin函数对其进行测试，Rastrigin函数是一个具有大量局部极优的典型复杂多峰函数(图2)，在运算过程中容易使算法陷入局部极优，却不能得到全局最优解，其表达式为式(14)。

-5.12≤xi≤5.12

(14)

将基本PSO算法与ASPSO算法分别运行50次，迭代终止条件为迭代误差达到1e-7，或迭代次数达到10 000次，测试并对比其收敛速度和精度，基本PSO算法与ASPSO算法反演Generalized Rastrigin函数(包括2维和5维)的参数设定如下：

基本PSO算法：m=30，w=0.9，c1=c2=1.8，vmax=5.12，xmax=5.12，xmin=-5.12。

ASPSO算法：m=30，w=0.5，c1=c2=1.8，vmax=5.12，xmax=5.12，xmin=-5.12，采用经典退火方式，初始温度T0=100 000，降温系数a=0.95。

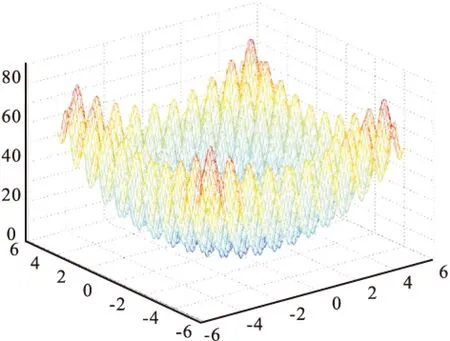
图2　Generalized Rastrigin函数Fig．2　Generalized Rastrigin function

两种算法基于Generalized Rastrigin函数的计算结果如表1所示，从表1中可以看出，ASPSO算法在收敛速度和精度上较普通PSO算法都有很大改善。对于复杂多峰Rastrigin函数，ASPSO算法运算效率是普通PSO算法6倍～20倍，并且解的质量有很大提高。

表1　基本PSO算法和ASPSO算法基于Generalized Rastrigin函数的结果对比

3模型验证

在地震勘探中，无噪时的地震道记录S(t)可以表示为反射系数r(t)与地震子波w(t)的褶积：

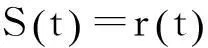
(15)

由方程(15)递推反演，可以得到弹性阻抗的递推公式：

(16)

弹性阻抗反演可以看作函数优化求极值问题，即要求取每个角道集的反射系数序列r(t)，使其与角度子波w(t)褶积后与实际地震记录之间的误差函数F(r)最小，则优化目标函数为式(17)。

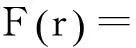
(17)

采用改进粒子群算法进行弹性阻抗反演的步骤如下：

1)抽角道集并提取各个角道集的子波。这里模型中抽取5°、25°、45°三个角道集作为观测值。

2)根据混合粒子群算法生成各角道集的反射系数序列r(t)，混合粒子群的每一维就对应地下每一地层的反射系数，任意粒子在反射系数空间进行搜索，每搜索到的一个新位置就相当于得到了一个反射系数序列的候选解，根据式(15)生成模型的地震道记录S(t)。

3)根据式(17)计算误差函数F(r)。

5)利用优化的粒子群算法进行迭代，优化最优解，直到满足截止条件。

作者将含有100个时间样点的测井曲线作为数据模型，采样间隔1 ms。混合粒子群算法的参数设置为：种群大小m=30；惯性因子w=0.1；学习因子c1=c2=1.8,xmin=-1，xmax=1，vmax=1，误差要求小于0.000 001；采用经典退火方式，初始温度T0=100 000，降温系数a=0.95。

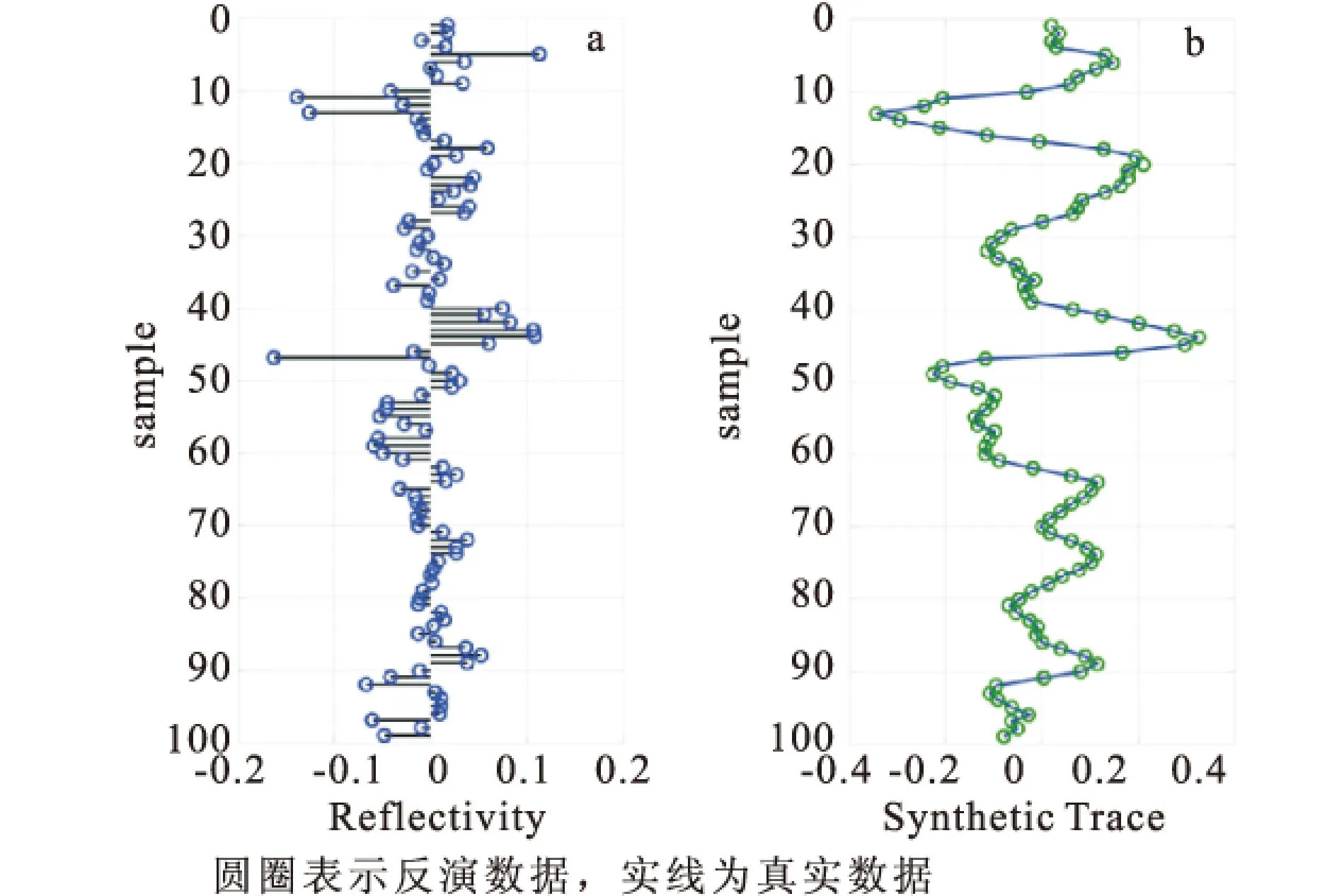
图3　角道集反演的反射系数和合成地震记录与真实的反射系数和实际地震记录对比Fig．3　The inversion coefficient of 5° gathers and synthetic seismic compare with the actual coefficient and records(a)反演的反射系数与实际反射系数对比;(b)反演的地震记录与实际地震记录对比

仅以5°角道集反演结果(图3)说明基于混合粒子群算法的弹性阻抗反演方法的有效性。从图3看出，反演得到的反射系数和地震记录与实际值都吻合得很好。根据此方法，分别反演得到5°、25°和45°角道集的反射系数序列，然后递推得出这三个角道集的弹性阻抗曲线，如图4所示。

得到三个角度的弹性阻抗曲线后，计算各层的纵波阻抗、横波阻抗、密度、纵波速度、横波速度等弹性参数(虚线)，以上参数曲线与原测井曲线对比如图5所示。由图5可以看出，反演得到的各弹性参数曲线与测井数据曲线吻合得很好。

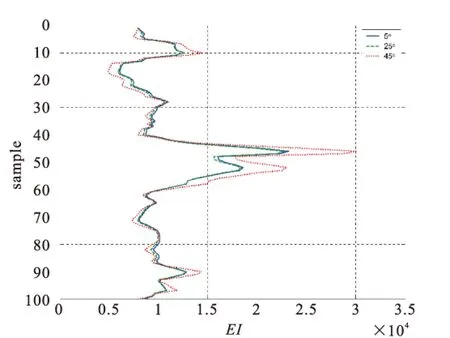
图4　反演得到的5°、25°、45°三个角度的EI曲线Fig．4　The EI inversion curves of 5°、25°、45°

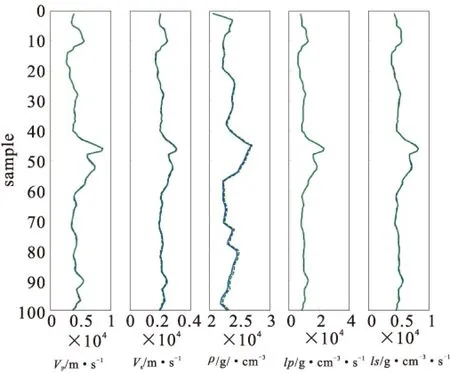
虚线表示根据反演的EI计算出的各弹性参数，实线表示原测井曲线图5　根据反演的EI计算出的各弹性参数与原测井曲线对比Fig．5　Comparison of the elastic parameters curves and the original logging curves

4应用实例及效果分析

选取胜利油田某工区二维数据进行弹性阻抗反演，对这里反演算法加以检测。该区原始道集数据信噪比低，层间反射杂乱，不利于AVO属性分析。为了使最终的叠前振幅数据能准确反映地下界面的反射强度，在反演之前需要对地震资料做以下振幅保持处理：①球面补偿；②地表一致性反褶积；③随机噪声衰减；④反Q滤波；⑤叠前时间偏移。

过da21井道集经预处理后(图6)，地震资料的品质得到较大改善，信噪比提高，随机噪声得到极大压制，目标层段(图6中黄色矩形所示)AVO现象明显，有利于进行叠地震属性的反演。

图6　过da21井预处理后道集Fig．6　Traces record after preprocessing over da21 well

通过对该区井资料的分析，发现该区沙二段为砂泥岩互层沉积，砂体单层厚度小，储层薄，纵向叠置，横向对比性较差，具有横向变化快、识别难度大的特点。图7为该区沙二段砂泥岩速度统计结果图，泥岩速度为2 000 m/s ～2 600 m/s，砂岩速度为2 600 m/s ～3 600 m/s，砂岩含油之后纵波速度有所下降。为此，AVO相应表现为振幅随偏移距的增大而减小，属第一类AVO。

图7　某工区da21井区沙二段砂、泥岩速度统计Fig．7　The velocity statistics of sandstone and 　mudstone of Es2 in da21 well

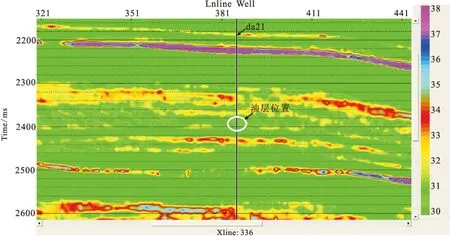
图8　弹性阻抗反演得到的过da21井λρ剖面Fig．8　Theλρsection with a well location of da21

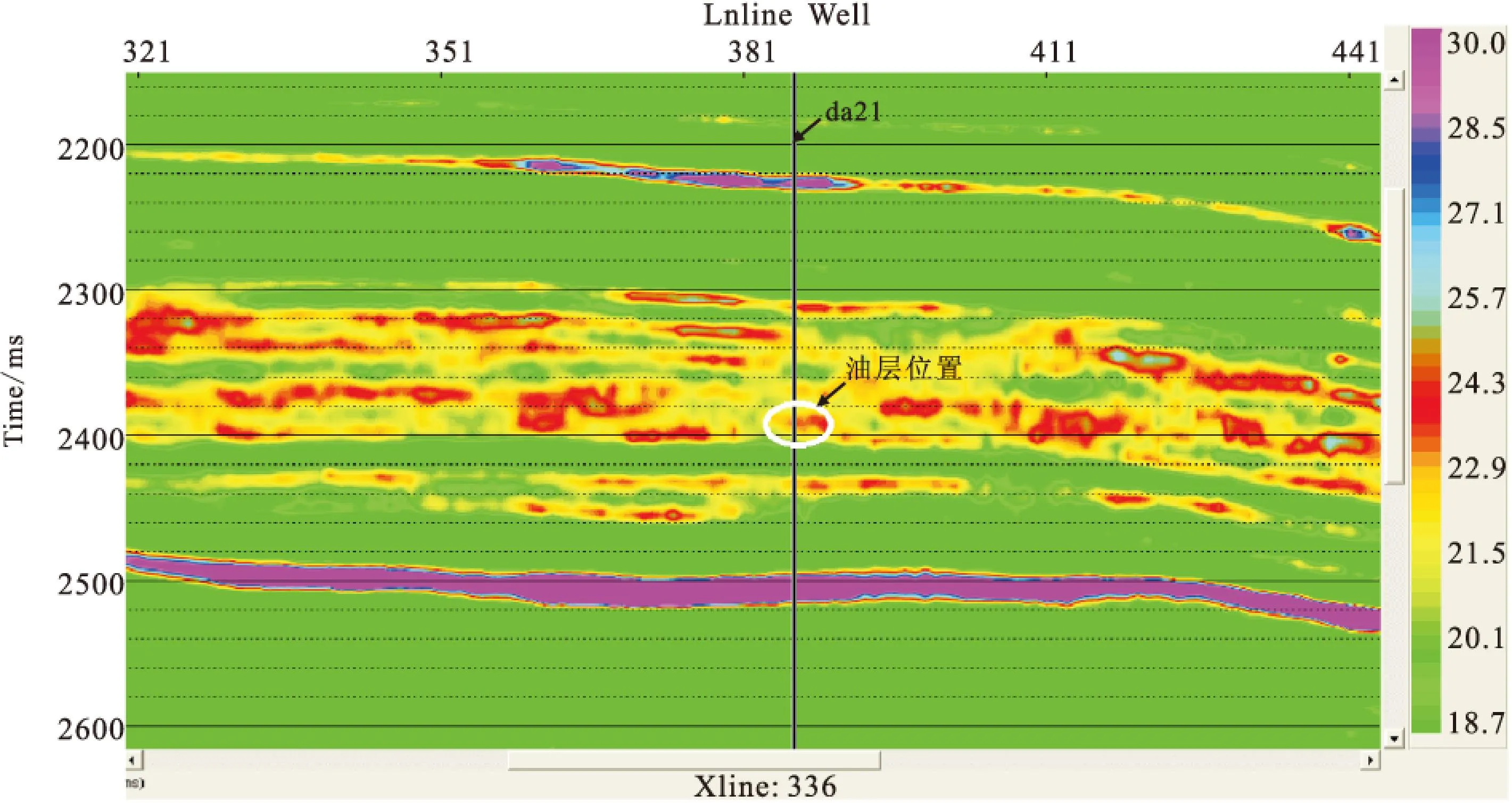
图9　弹性阻抗反演得到的过da21井μρ剖面Fig．9　Theμρsection with a well location of da21

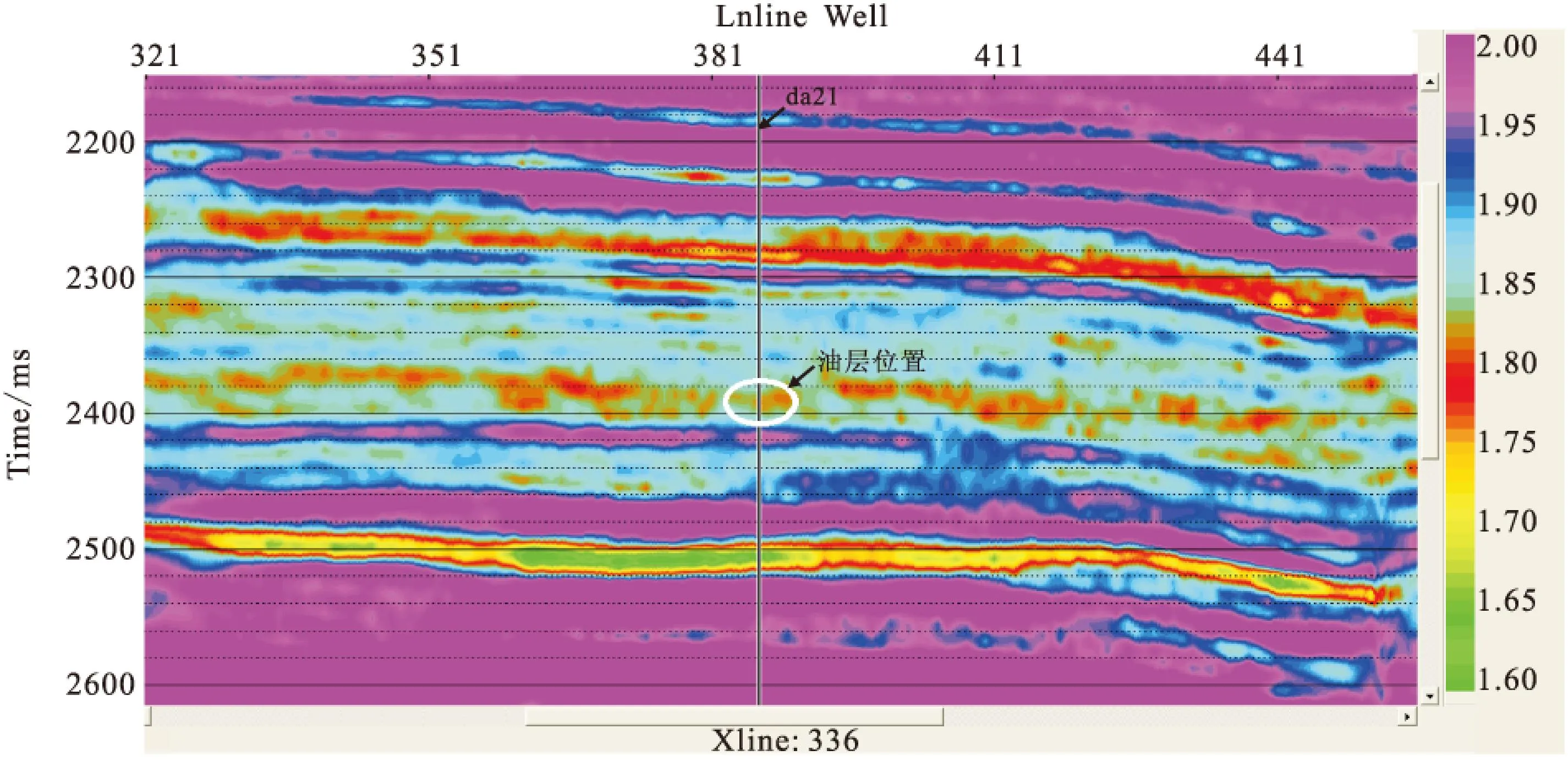
图10　弹性阻抗反演得到的过da21井VP/VS剖面Fig．10　The VP/VS section with a well location of da21

5结论与认识

弹性阻抗反演的提出，使波阻抗反演从叠后发展到叠前，可获得多种叠后资料无法得到的信息。目前，弹性阻抗反演通常采用广义线性反演算法，易陷入局部极优、强烈依赖于初始模型。本文将粒子群算法应用于弹性阻抗反演中，通过对每一代进化产生的粒子进行随机摄动，并加入模拟退火算子，改善了收敛速度和精度，用测井数据加以验证并应用于胜利油田某工区实际资料的弹性阻抗反演中。提取了多种叠前地震属性剖面。该方法提取的属性剖面能够反映储层特征，与测井结果相符，说明基于改进粒子群算法的弹性阻抗反演方法切实有效，可以服务于岩性识别和油气预测。

参考文献：

[1] CONNOLLY P. Elastic Impedance[J].The Leading Edge,1999,18(4):438-452.

[2] CAMBOIS G.AVO inversion and elastic impedance [J].SEG Technical Program Expanded Abstracts, 2000,70:142-145.

[3]MALLICK S.AVO and elastic impedance [J].The Leading Edge,2001,20 (10):1094-1104.

[4]WHITCOMBE D N. Elastic impedance normalization [J].Geophysics,2003,67(1):60-62.

[5]WHITCOMBE D N.Extended elastic impedance for fluid and lithology prediction [J].Geophysics,2002,67(1):63-67.

[6]马劲风.地震勘探中广义弹性阻抗的正反演[J].地球物理学报,2003,46(3):118-124

MA J F.Forward modeling and inversion method of generalized elastic impedance in seismic exploration [J].Chinese Journal of Geophysics,2003,46(3):118-124.(In Chinese)

[7]SUBHASHIS MALLICK.A simple approximation to the P-wave reflection coefficient and its implication in the inversion of amplitude variation with offset data[J].Geophysics,1993,58(4):544-552.

[8]YANGHUA WANG.Approximations to the Zoeppritz equations and their use in AVO analysis[J].Geophysics,1999,64(6):1920-1927.

[9]倪逸.弹性阻抗计算的一种新方法[J].石油地球物理勘探,2003,38(2):147-155.

NI Y.A new method for calculation of elastic wave impedance[J].OGP,2003,38(2):147-155.(In Chinese)

[10]印兴耀,袁世洪,张繁昌.从弹性波阻抗中提取岩石物性参数[C].北京：CPS/SEG 2004国际地球物理会议,2004.

YIN X Y,YUAN S H,ZHANG F C.Extraction of rock physical properties from elastic wave impedance.[C],Beijing:CPS/SEG 2004 International Geophysical Conference，2004.(In Chinese)

[11]王保丽,印兴耀,张繁昌.基于Gray近似的弹性波阻抗方程及反演[J].石油地球物理勘探,2007,42(4):435-439.

WANG B l,YIN X Y,ZHANG F C.Gray approximation-based elastic wave impedance equation and inversion[J].OGP,2007,42(4):435-439.(In Chinese)

[12]杨文采.地球物理反演的理论与方法[M].北京:地质出版社,1997.

YANG W C.Theories and methods of geophysics inversion [M].Beijing:Geological Publishing House,1997.(In Chinese)

[13]杨维,李歧强.粒子群优化算法综述[J].中国工程科学,2004,6(5):87-94.

YANG W,LI Q Q.Review of particle swarm optimization algorithm[J].China Engineering science,2004,6(5):87-94.(In Chinese)

[14]EBERHART R,KENNEDY J.A new optimizer using particle swarm theory[A].IEEE Proceedings of the sixth international symposium on micro machine and human science.Piscataway:IEEE Service Center,1995.39-43.

[15]KENNEDY J,EBERHART.Particle swarm optimization[A].IEEE Proceedings of international conference on neural networks[C].Piscataway:IEEE Service Center,1995.1942-1948.

[16]曾建潮,介倩,崔志华.微粒群算法[M].北京:科学出版社,2004.

ZENG J C,JIE Q,CUI Z H.Particle swarm optimization[M].Beijing:Science Press,2004.(In Chinese)

收稿日期：2015-03-30改回日期：2015-06-11

基金项目:国家自然科学基金(41004046,41230318)

作者简介：张进(1978-)，男，博士，副教授，主要从事地震资料叠前反演，E-mail:zj515@ouc.edu.cn。

文章编号：1001-1749(2016)03-0353-08

中图分类号：P 631.4

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.03.10

Application of particle swarm optimization in prestack elastic impedance inversion

ZHANG Jin, CHEN Xiao-qi, XING Lei, AN Ling-fang, ZHAO Xi, AN Zhen-fang

(Key Lab of Submarine Geoscience and Prospecting Techniques,Ministry of Edecation,Ocean University of China,Qingdao266100,China)

Abstract:Elastic impedance inversion is a combination technology of acoustic impedance inversion and AVO inversion, which can overcome the defects of post-stack impedance inversion and reflect the amplitude variation with offset. Elastic impedance inversion has been widely used to identify lithology and fluid. While conventional linear elastic impedance inversion methods strongly depend on the initial model and easily fall into local minimum, a nonlinear elastic impedance inversion based on improved particle swarm optimization is presented, which has been verified by model test. Finally, we applied this new inversion algorithm to the prestack seismic data in Shengli oilfield and achieved several elastic parameter profiles, which are consistent with the drilling results. The method has been proved to be a feasible and effective way for complex reservoir exploration.

Key words:elastic impedance inversion; particle swarm optimization; nonlinear inversion